基于曹妃甸工业区的坐标转换精度分析*

杨久东，田聪颖

(河北联合大学矿业工程学院，河北唐山 063009)

0 引言

转换精度是区域性坐标系统转换中的关键问题，在曹妃甸工业区，常用坐标系统主要有唐山城市坐标系和WGS－84坐标系，构建二维参心坐标系与用GPS方法建立的三维地心坐标系间高精度的转换关系一直以来是规划和国土等管理部门以及测绘单位关心的重要问题。

曹妃甸工业区常用坐标系主要是唐山城市坐标系和WGS－84坐标系，唐山城市坐标系采用了1954年北京坐标系的参数，采用克拉索夫斯基椭球，大地原点在前苏联的普尔科沃天文台，椭球参数:长半轴 a=6 378 245 m;短半轴 b=6 356 863.018 8 m;扁率 α =1/298.3;WGS－84坐标系属于地心坐标系，采用84椭球，坐标原点在地球质心，椭球参数a=6 378 137 m;b=6 356 752.314 2 m;扁率 α =1/298.257 223 6。模型的转换参数用已知点的空间坐标求解［2］，已有研究表明大地高的精度对平面坐标转换的影响很小［3，4］，转换的精度除了取决于坐标转换的模型外，还与求解转换参数的公共点坐标精度、公共点个数和公共点的分布有关［5－7］。

不同坐标系间的转换模型有很多，主要有3参数模型、4参数模型、多项式转换法、方格网法、7参数转换模型等。国内应用较为广泛的有4参数模型和7参数模型。4参数转换模型计算公式为:

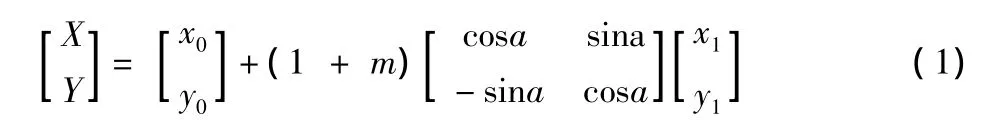
式中:X、Y为待求坐标;x0、y0是平移参数;m为尺度参数;a为旋转参数;x1、y1为待转换源坐标。常用的Bursa七参数转换模型计算公式为:

1 坐标转换模型

区域坐标转换的具体做法是选取几个同时具有不同坐标系统中的坐标的已知点，然后推算出相关参数，建立两个坐标系统之间的转换函数模型，从而进行两个系统之间的转换。转换方法的选择需根据转换地区的实际情况进行选定［1］。7参数转换

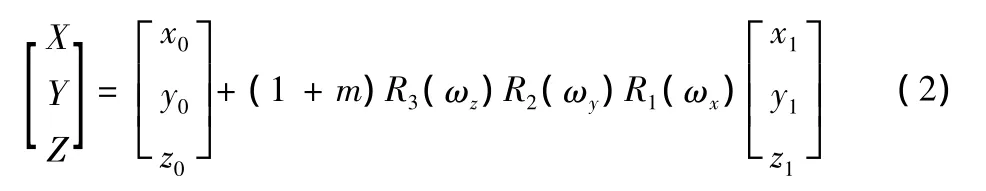
式中:X、Y、Z为待求坐标;x0、y0、z0是平移参数;m为尺度参数;x1、y1、z1为待转换源坐标;R3(ωz)、R2(ωy)、R1(ωx)为旋转参数的矩阵，其中:

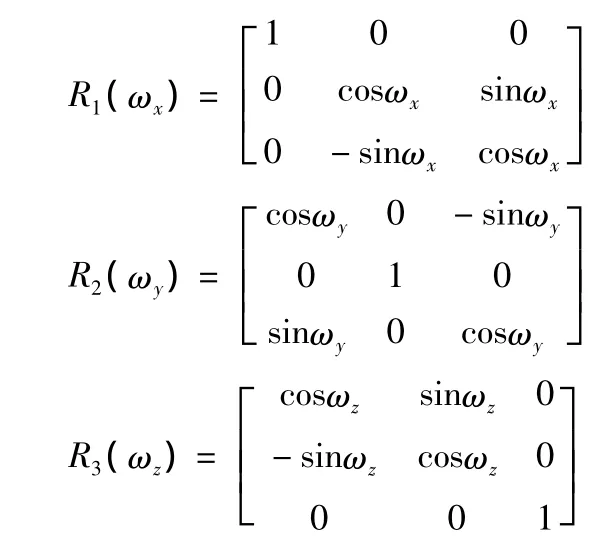
2 公共点的选择对转换精度的影响

为验证上述转换方法的转换精度，利用唐山曹妃甸工业区内的14个控制点，这些点同时具有两种坐标系(唐山城市坐标、WGS－84坐标)的成果，高程分别为水准高和大地高，外围控制点连线的控制面积约为490 km2，成果见表1，其分布关系如图1所示。根据参与解算参数的控制点的点数和分布情况，共设计了14种实验方案(见表2)。

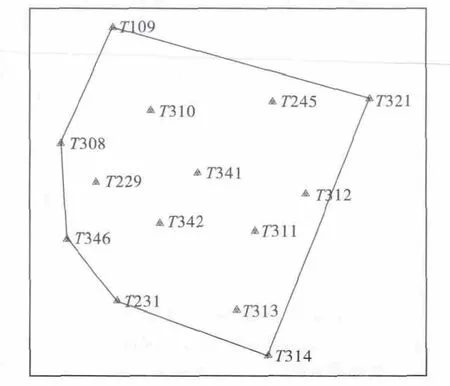
图1 控制点分布图Fig.1 Distribution of control points

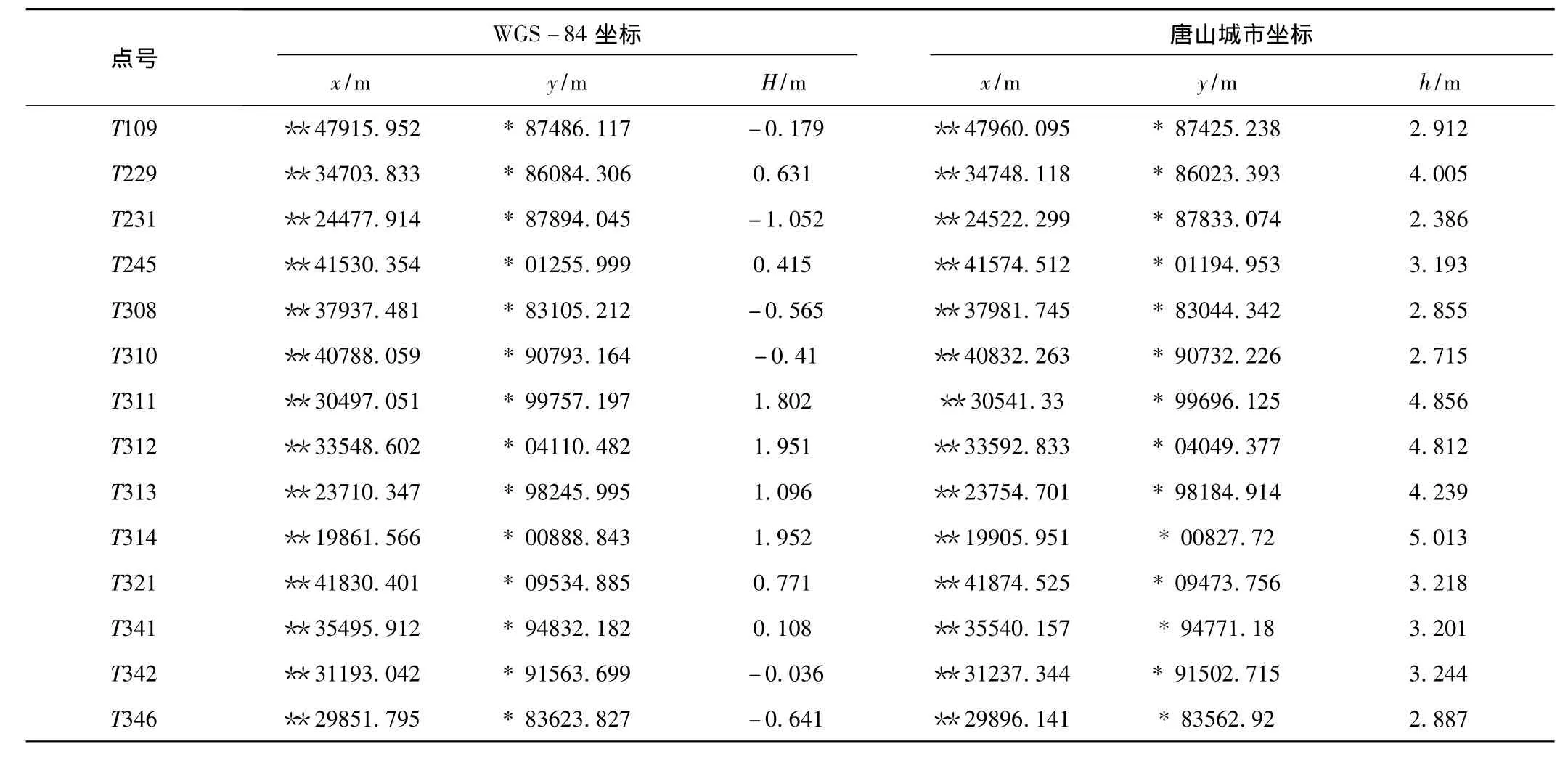
表1 控制点坐标Tab.1 Coordinates of control points

表2 14种实验方案统计表Tab.2 Statistics of 14 kinds of experimental plans

根据表2中的各种方案分别计算出曹妃甸地区WGS－84坐标向唐山城市坐标进行坐标转换的7参数和4参数，以求得的参数利用7参模型和4参模型求出表1中全部14个控制点的转换结果，并以其作为参照对象，对转换结果与原有坐标进行比较，计算出转换坐标与原有坐标的差异量，实验结果统计分别列于表 3、表 4、表 5。

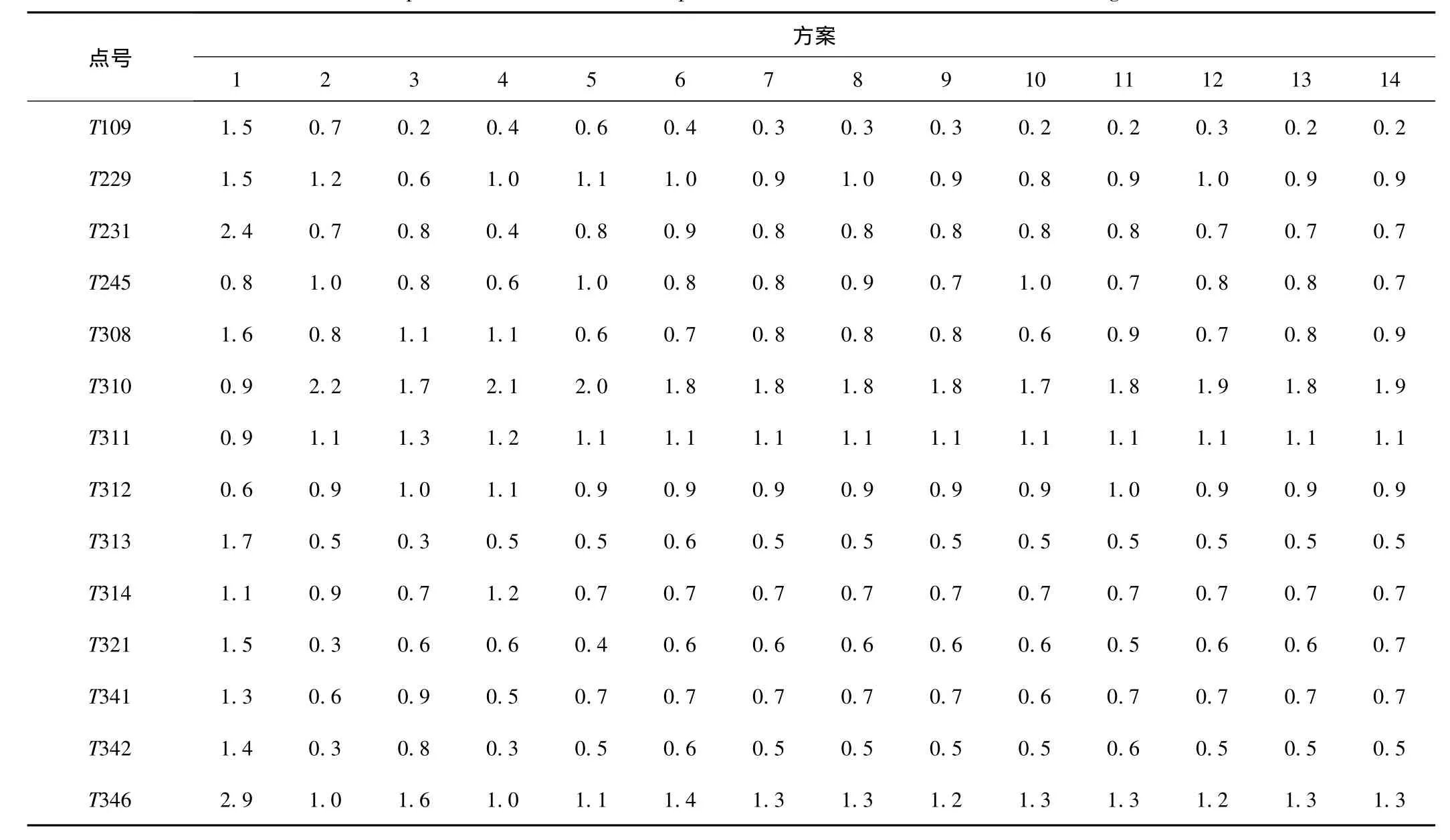
表3 7参数转换坐标与原有坐标的点位误差统计表 (单位:mm)Tab.3 Statistics of point errors between seven parameter transformation coordinate and original coordinate (Units:mm)

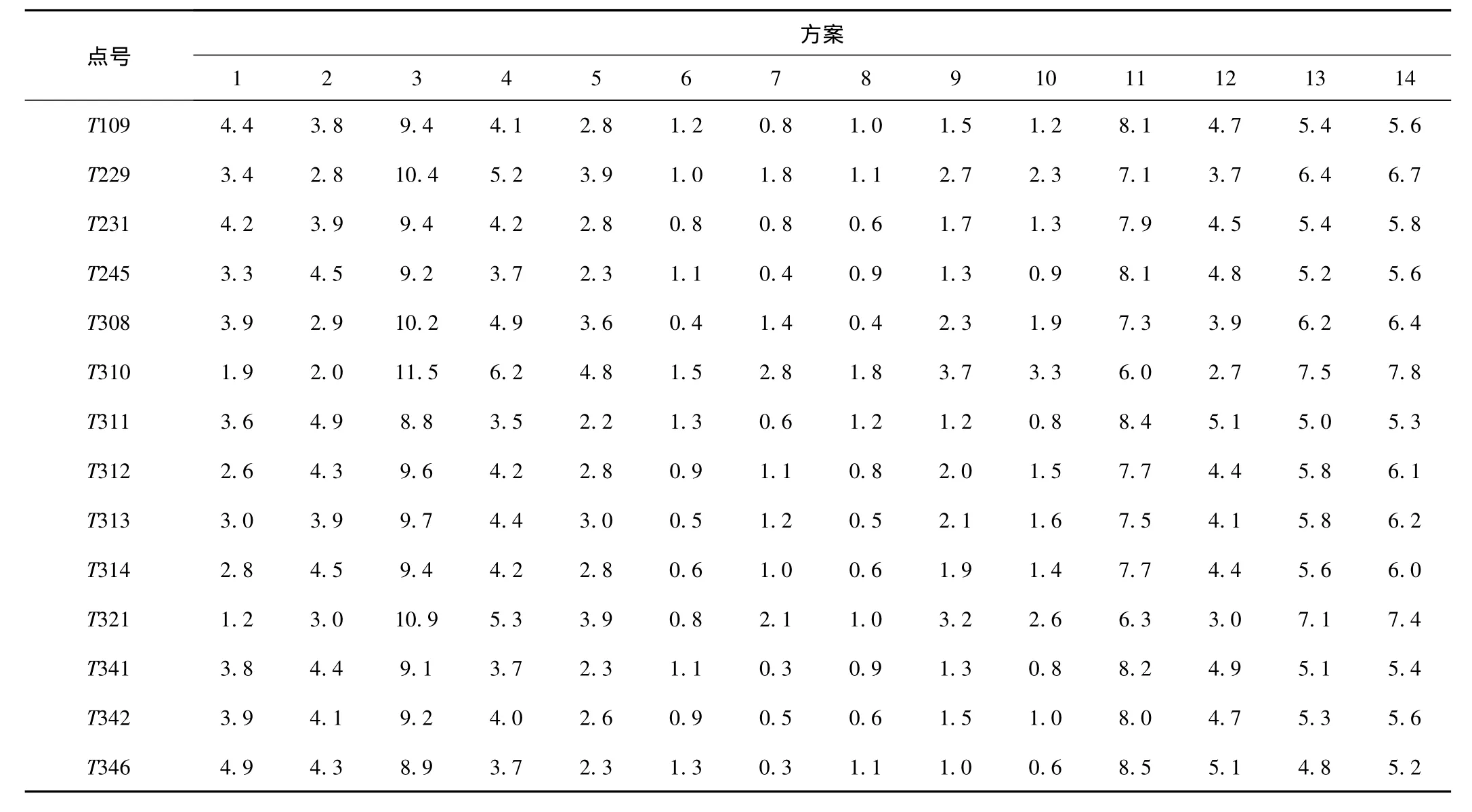
表4 4参数转换坐标与原有坐标的点位误差统计表 (单位:mm)Tab.4 Statistics of point errors between four parameter transformation coordinate and original coordinate (Units:mm)

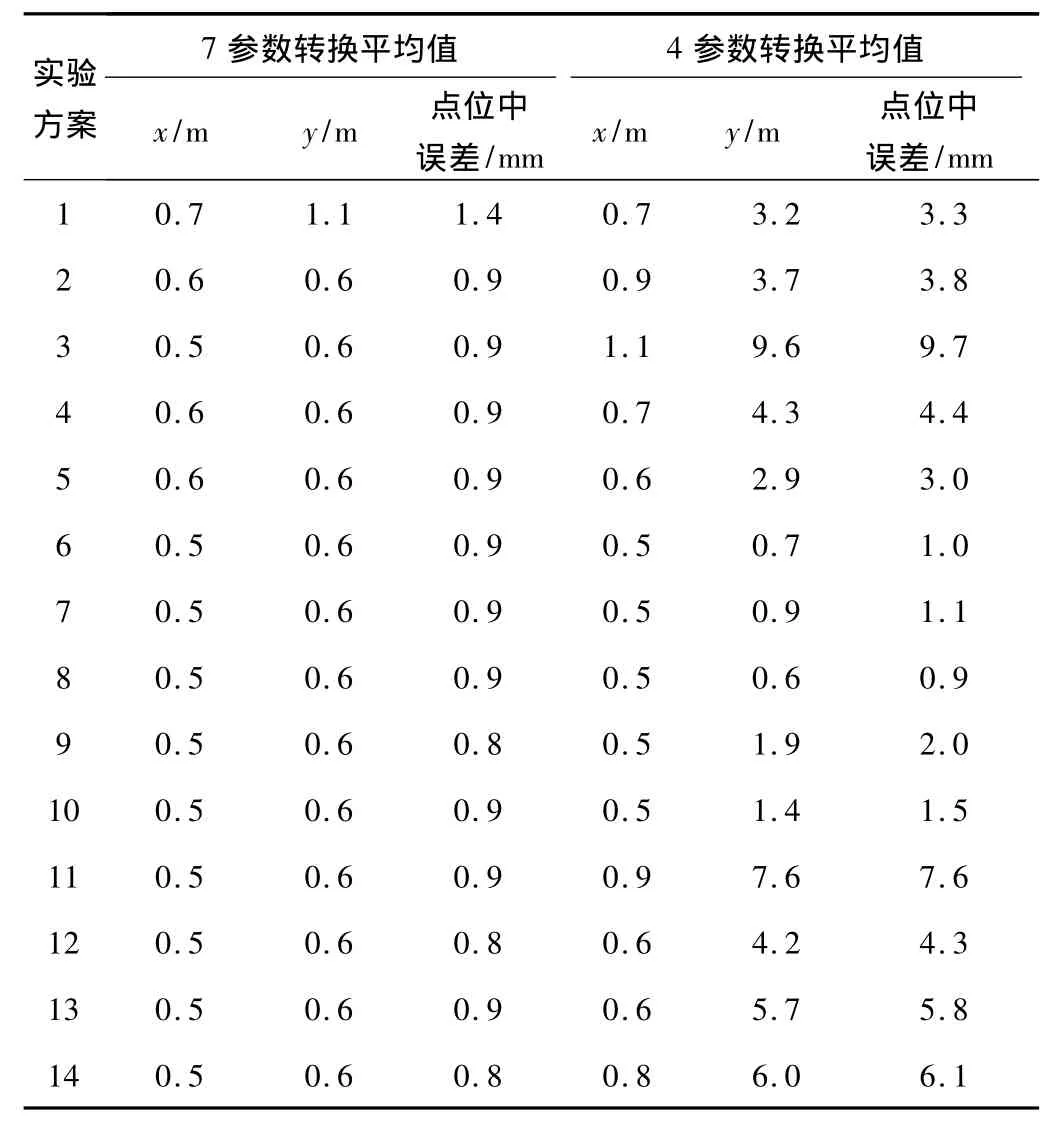
表5 转换坐标与原有坐标的差异量统计Tab.5 Statistics of differences between transformation coordinate and original coordinate

分析表3到表5的统计数据可知:

1)7参数转换平面点位中误差除方案1为1.4 mm外，其余方案均在0.8～0.9 mm，且随着控制点数量的增加及控制点分布不同对精度没有明显影响。

2)从4参数结果可以看出，平面点位中误差由0.9～9.7 mm，随着控制点选择不同精度波动较大。

3)分析方案1至3的结果可知，所选控制点的控制范围对转换精度的影响很大，位于控制点控制范围以外的点的转换精度较差。

4)分析方案3～14的4参数转换结果可知，公共点的选择对4参数的求解影响很大，方案8单位中误差为0.9 mm，为最好;方案6和方案7的转换精度也很好，分别为1.0 mm和1.1 mm。结果表明，参与4参数计算的控制点除了应分布在控制区域的外围角点并能控制转换区域外，在转换区域的中间选取2～3个分布均匀的控制点是必要的。参与4参数计算的控制点的数量并非越多越好，当控制点数达到一定数量后，增加公共点的数量还有可能降低转换精度。

3 已知点误差对转换精度的影响

好的转换精度是建立在高精度的已知成果的基础之上的，实验数据选用的两种坐标系坐标是GPS静态控制方法获得的该区域高等级的测量控制成果，且为同期数据，成果的平面中误差为±0.46 mm。为了验证已知控制点精度对坐标转换结果的影响，在前述实验方案5的 T341点上随机加上2 cm、5 cm、10 cm、20 cm的误差。实验结果，如表6所示。

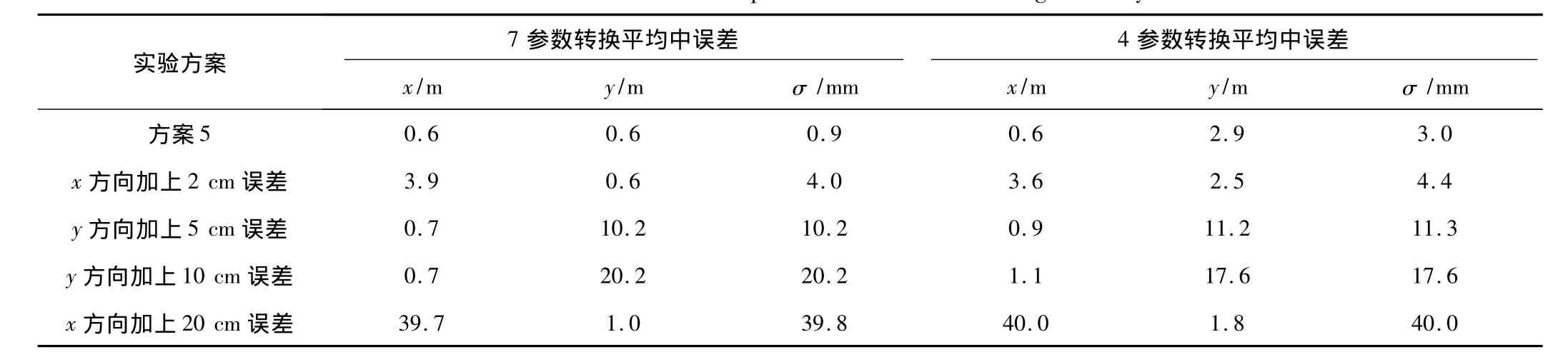
表6 点位误差对解算精度影响统计表Tab.6 Statistics of effect of position error on calculating accuracy

分析表6的统计数据可知:已知点的精度影响7参数法和4参数法的转换结果的精度，且转换误差的大小和方向与已知点误差存在相关性。

4 结论

在曹妃甸工业区范围内用利用基于三维转换模型的Bursa七参数法进行WGS－84坐标与唐山城市坐标的转换平面转换精度及稳定性均优于基于二维模型的4参数法，坐标转换精度约为1 mm，转换结果可靠。实践证明，一味地增加公共点数量并不能保证4参数转换精度的提高，当选择的公共点分布均匀且数量合理时，利用4参数法进行坐标转换也是可行的;控制点的误差会影响平面坐标转换精度，且转换误差的大小和方向与已知点误差存在正相关性。

［1］王履华.第二次土地调查中坐标系统转换方法研究［J］.测绘与空间地理信息，2010(1):48－51.

［2］葛燕飞.局部区域WGS－84、北京54及80西安坐标转换的应用研究［D］.昆明:昆明理工大学，2010.

［3］王文利，郭春喜，程传录.大地高误差对Bursa七参数平面转换精度的影响［J］.测绘科学，2011(5):37－38.

［4］王明孝，陈建斌，赵秀杰，曹学诚.大地高误差对坐标系转换精度的影响［J］.测绘工程，2013(3):8 －11.

［5］耿晓燕.地方独立坐标系向2000国家大地坐标系转换研究［D］.西安:西安科技大学，2010.

［6］邓勇，张正禄，黄江雄，等.工程测量中的坐标转换相关问题探讨［J］.测绘科学，2011(5):28 －30.

［7］陶叶青，杨娟.顾及观测误差的平面坐标系统转换方法［J］.测绘科学，2013(6):160 －161，184.