轮胎骨架材料带束层的有限元分析*

李 利，王 瑞，党 栋，王振鲁

(青岛科技大学 机电工程学院，山东 青岛 266061)

子午线轮胎是复杂的结构体，由橡胶和橡胶/钢丝帘线复合材料组成，在未充气时，不能承受较大的载荷，但当充气压力达到一定程度时却能承受较大的载荷，满足模型性能的要求[1-2]。在轮胎的运行中，骨架材料带束层是主要的受力构件之一，轮胎的许多性能都与带束层密切相关[3]，例如操作性能、安全性能、耐磨性、牵引性、滚动阻力等。因此，本文研究的重点是分析子午线轮胎在充气工况下充气压力与轮胎外直径、断面宽度的关系以及在静载荷工况下带束层各层的应力分布规律、径向力曲线、胎肩位置的周向向变形曲线，对以后进行测量橡胶钢丝的粘合性能时所施加载荷大小、试样弯曲范围有非常重要的指导意义。

1 轮胎有限元模型的建立

本文所研究的轮胎的型号是195/65R15。查阅橡胶工业手册，得到195/65R15子午线轮胎的设计尺寸，利用AutoCAD软件，绘制轮胎二维结构图，并将图形保存为*.dxf格式。图1为轮胎断面图及材料分布情况。

在ABAQUS中对轮胎进行建模，首先将AutoCAD绘制的图1导入到ABAQUS中，然后将二维图形转变成三维图。对轮胎模型进行属性定义，轮胎主要部件的材料特性参数如表1和表2[4]所示。

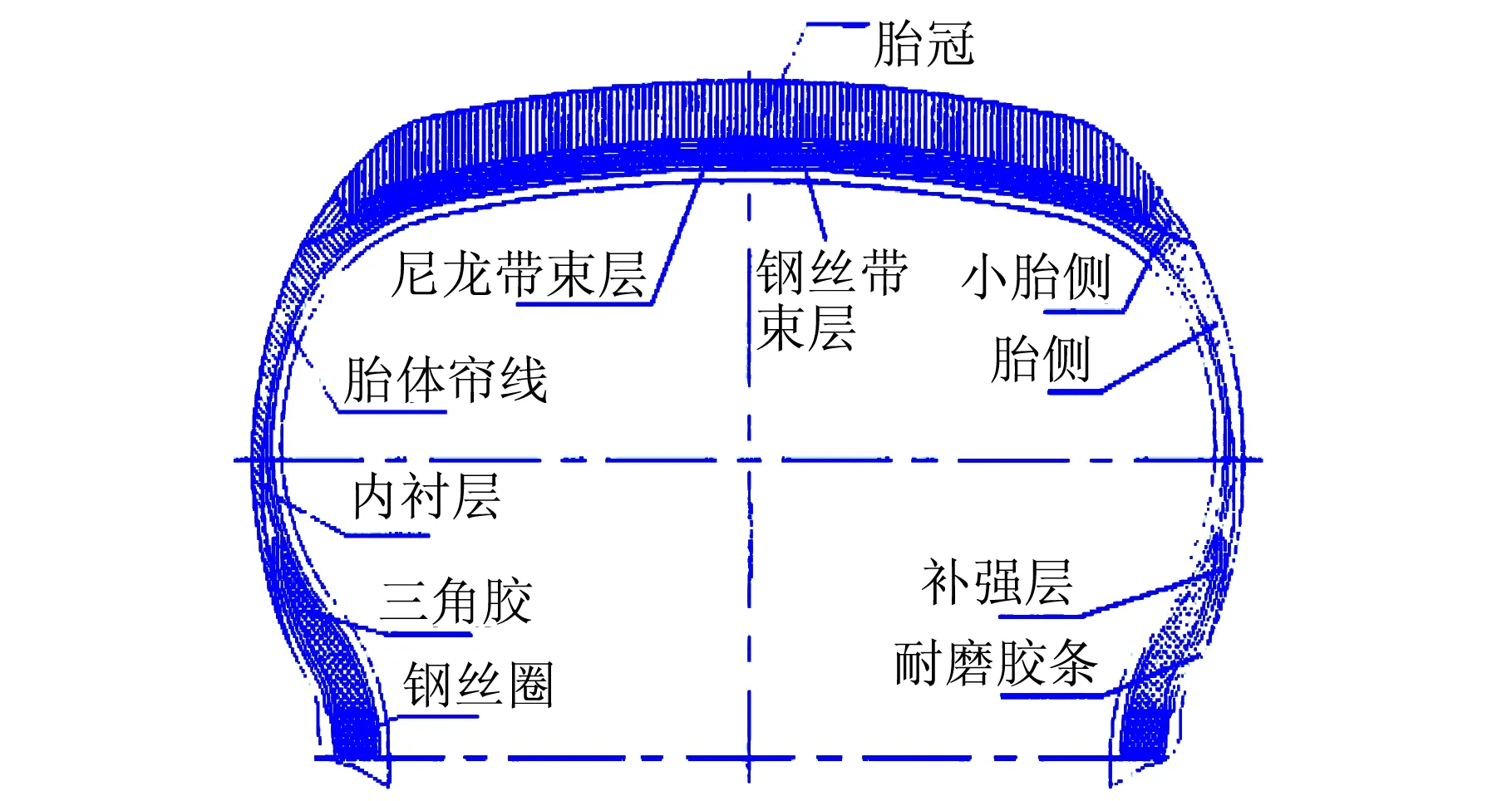
图1 轮胎断面图及材料分布情况

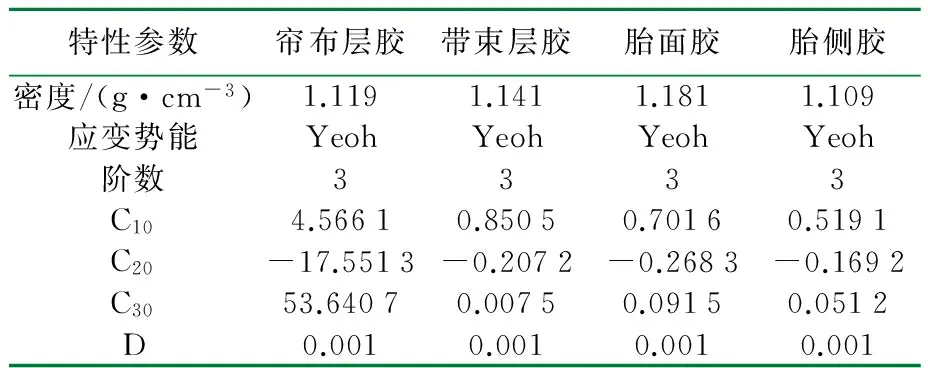
特性参数帘布层胶带束层胶胎面胶胎侧胶密度/(g·cm-3)1.1191.1411.1811.109应变势能YeohYeohYeohYeoh阶数3333C104.56610.85050.70160.5191C20-17.5513-0.2072-0.2683-0.1692C3053.64070.00750.09150.0512D0.0010.0010.0010.001

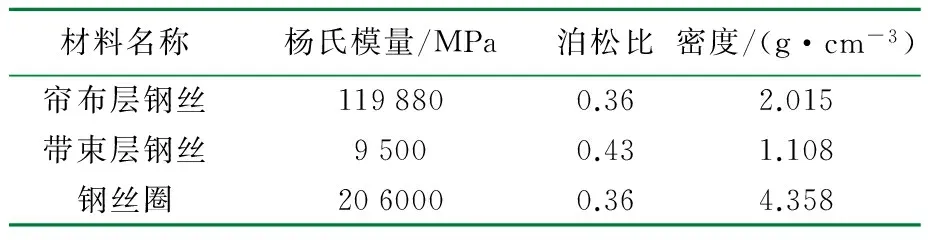
表2 轮胎骨架材料的参数

在组装之前要建立一个地面，使它与轮胎相接触，其中地面是刚性体。通过查看资料，最终本文所选择的单元类型为C3D8R，即八节点、线性、缩减积分和沙漏控制的空间单元模型。将轮胎骨架、轮辋、地面按照相应的位置组装起来。图2、图3为在上述参数基础上建立的轮胎有限元二维及三维模型。

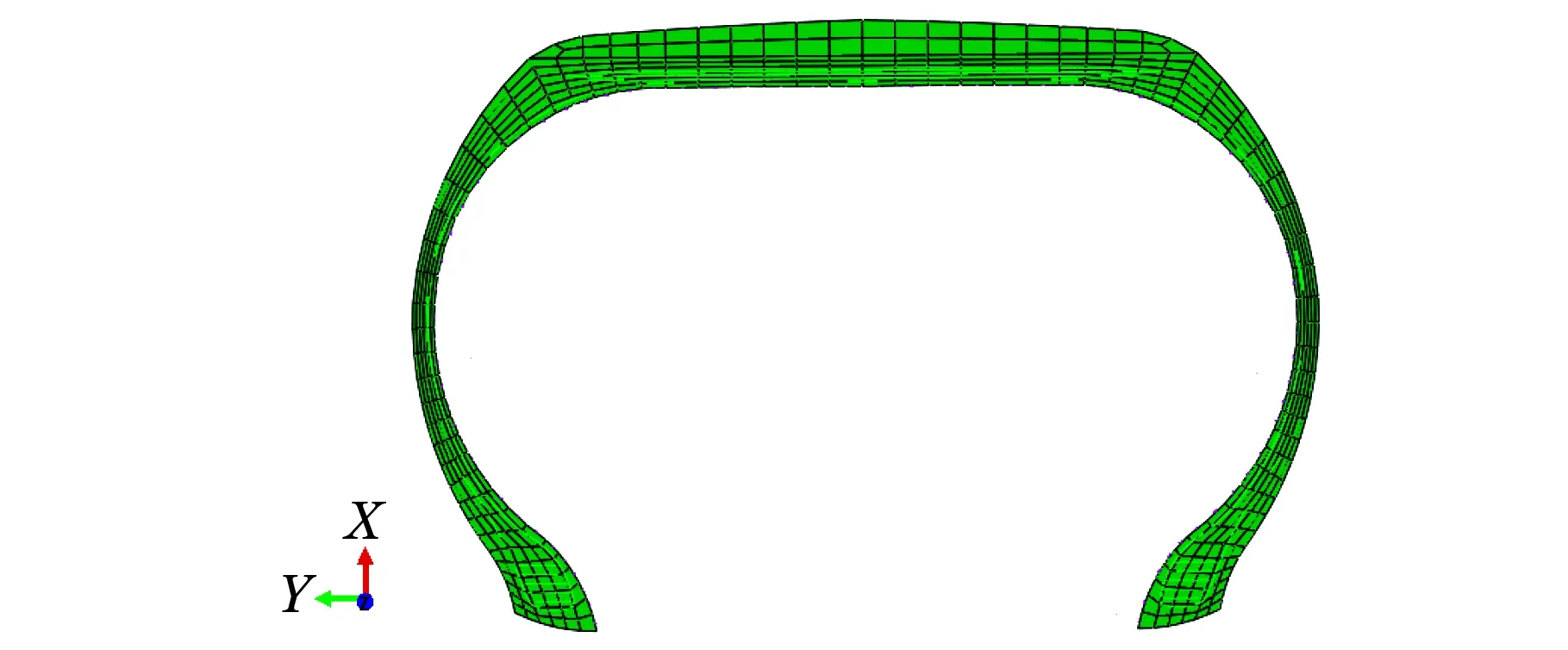
图2 二维子午线轮胎有限元模型

图3 三维子午线轮胎有限元模型

2 轮胎充气工况分析

通过模拟充气过程，是在0～450 kPa的气压下，把气压分成若干小步逐步对轮胎进行加载，确保压力载荷逐步加载到相应的单元面上，最终得到轮胎充气压力与充气外直径之间的关系曲线[5]，如图4所示。

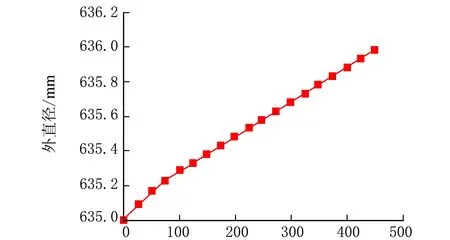
充气压力/kPa 图4 轮胎充气压力与充气外直径之间的关系

从图4可以看出，在充气初期，轮胎直径有较大的变化，主要是因为橡胶的弹性模量比较小，所以导致变形比较大。但随着充气压力增大，轮胎直径的变形减小，这时带束层中的钢丝帘线及胎体中的帘线也发生变形，但由于钢丝的弹性模量比较大，在增长相同压强的条件下，轮胎的变形相对减小。从整体图形来看，轮胎充气压力与轮胎直径近似呈线性关系。

图5是轮胎充气压力与轮胎断面宽度的关系曲线。从图5可以看出，充气压力小于100 kPa时，轮胎断面宽度增长得很快，这是由于轮胎在压强的作用下体积迅速扩大；充气压力大于100 kPa时，断面宽度增长比较缓慢，由于胎圈与轮辋之间存在摩擦，故断面宽度与气压不呈线性关系，但是从整体上还可以看作是线性关系。

充气压力/kPa图5 轮胎充气压力与断面宽度间的关系

3 轮胎静载荷工况分析

3.1 轮胎整体受力分析

对轮胎静负荷的模拟主要有以下4种方式[6]：(1)地面固定，在轮辋上施加一定的位移量；(2)地面固定，在轮辋上作用一定的集中力载荷；(3)轮辋固定，在地面施加一定的位移量；(4)轮辋固定，在地面上作用一定的集中力载荷。因本次测量是轮胎的受力载荷与变形之间的关系，所以，本次模拟所使用的方案是轮辋固定[7]，在地面上作用一定的集中力载荷，载荷施加的位置为参考点RP，方向由地面指向轮胎。

轮胎充气工况后，通过地面参考点RP向轮胎施加垂直载荷用于模拟轮胎的加载过程，即给参考点RP一定的位移和载荷。加载过程中轮辋是完全固定的，忽略地面与轮胎间的摩擦。静载荷作用下，轮胎与地面接触区域发生明显的变形，如图6所示。

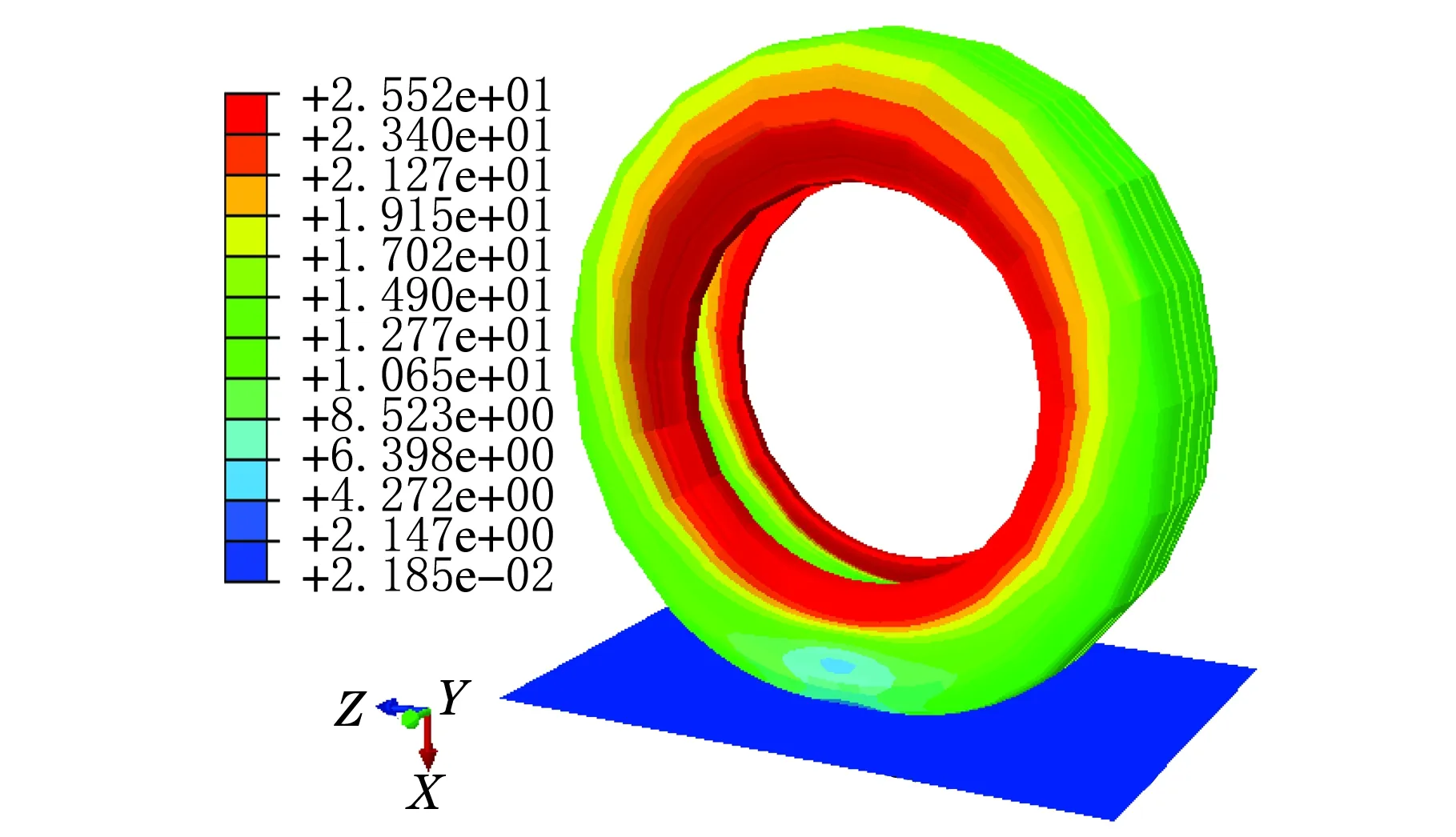
图6 静负荷下轮胎受力变形

从图6可以看出，轮胎与地面的接触部位发生明显变形，该变形量的最大值约为25.52 mm。在标准轮胎内压为450 kPa气压下，应用ABAQUS对模型逐步施加载荷进行模拟，建立了轮胎下沉量与载荷之间的关系曲线，如图7所示。

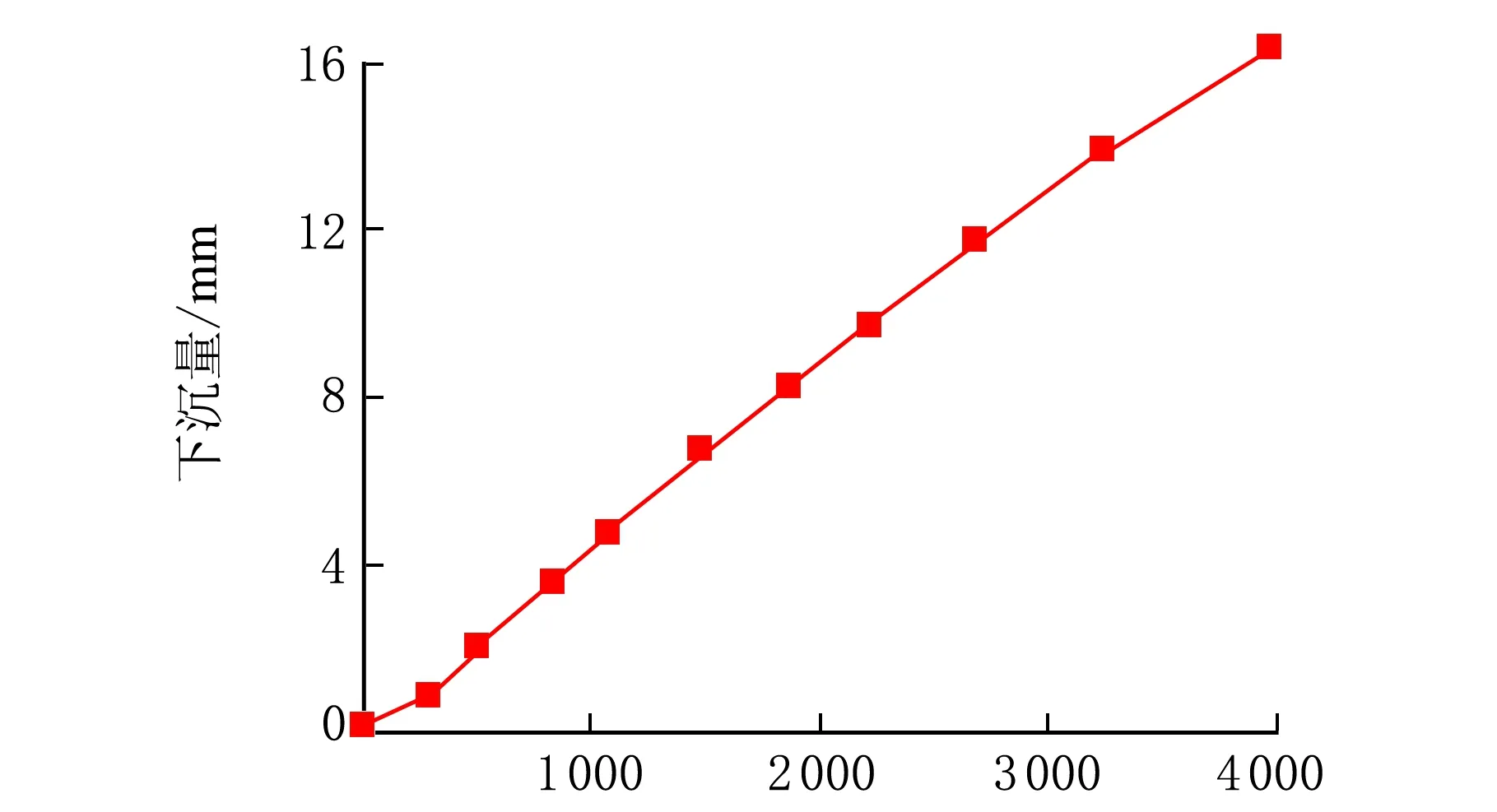
静载荷/N图7 轮胎下沉量与载荷间关系

从图7可以看出，当外载荷小于1 000 N时下沉量与载荷关系是非线性的，这是由于轮胎在加载过程中产生硬化现象，当外载荷大于1 000 N时轮胎的径向刚度趋于稳定，下沉量与载荷关系可近似看作是线性的，这与实际情况相符[8]。

3.2 轮胎骨架材料带束层的应力分析

带束层是子午线轮胎的主要受力部件之一，轮胎的耐磨性、安全性、牵引性、裂口等问题都与带束层有关，所以研究带束层的应力分布具有极其重要的意义。本文主要针对带束层部位进行应力及变形的分析。本次分析的带束层主要由两层组成，与胎体较近的为第一层带束层，与胎体较远的为第二层带束层。

在4 000 N的静载荷和450 kPa充气压力的作用下，带束层内部应力发生了变化。从图8与图9可以看出：在非接地部位带束层端部的应力很小，越往内应力值有所增大；在外载荷的作用下轮胎与地面发生接触，轮胎与地面接触部位有较大的局部变形，接触区域的轮胎轮廓变为扁平状；胎肩位置的应力值最大；从上向下看越接近接地端应力值越大；可以近似地看作应力值是关于竖直轴线对称；第一带束层的应力值大于第二带束层。

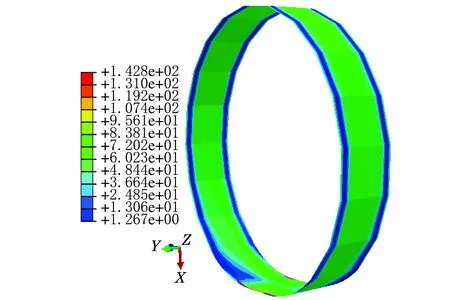
图8 第一层带束层非接地处应力图

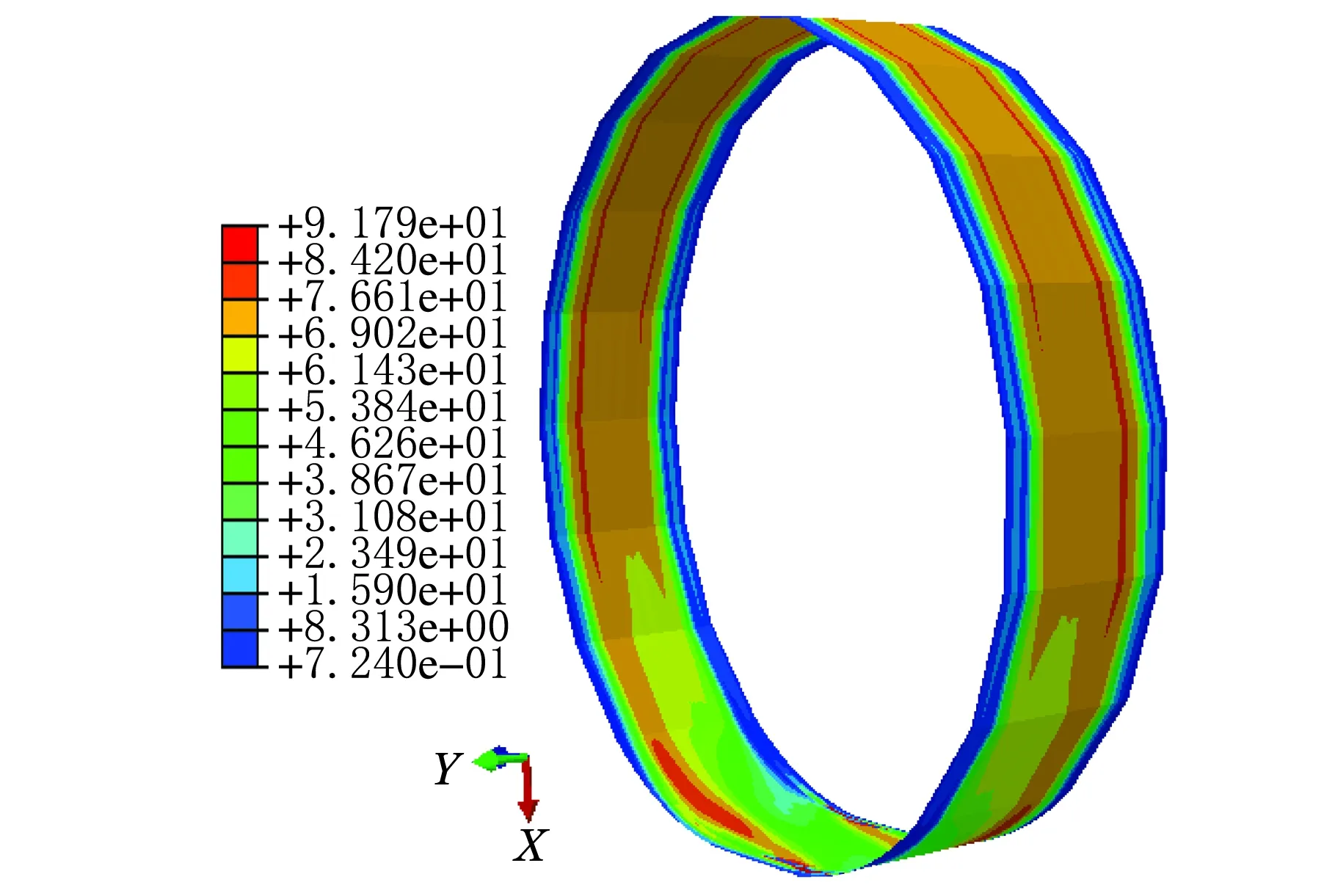
图9 第二层带束层非接地处应力图

图10和图11为轮胎接地处的带束层的应力图。从图10和图11可以看出：第一带束层的最大应力值发生在端部且最大值约为142.8 MPa，第二带束层端部的应力值较小，最大值在大约胎肩的部位且最大应力值约为91.79 MPa，因为在设计带束层结构时第一带束层与第二带束层的宽度不相同，第一带束层的端部靠近胎肩的位置，第二带束层端部在胎肩的外侧；接地区域应力的分布图是以接地中心为中心的对称图形；接地中心的应力值相对两边的较小，只是由于轮胎在载荷的作用下接地区域的中部产生皱曲现象。

图10 第一层带束层接地处应力图

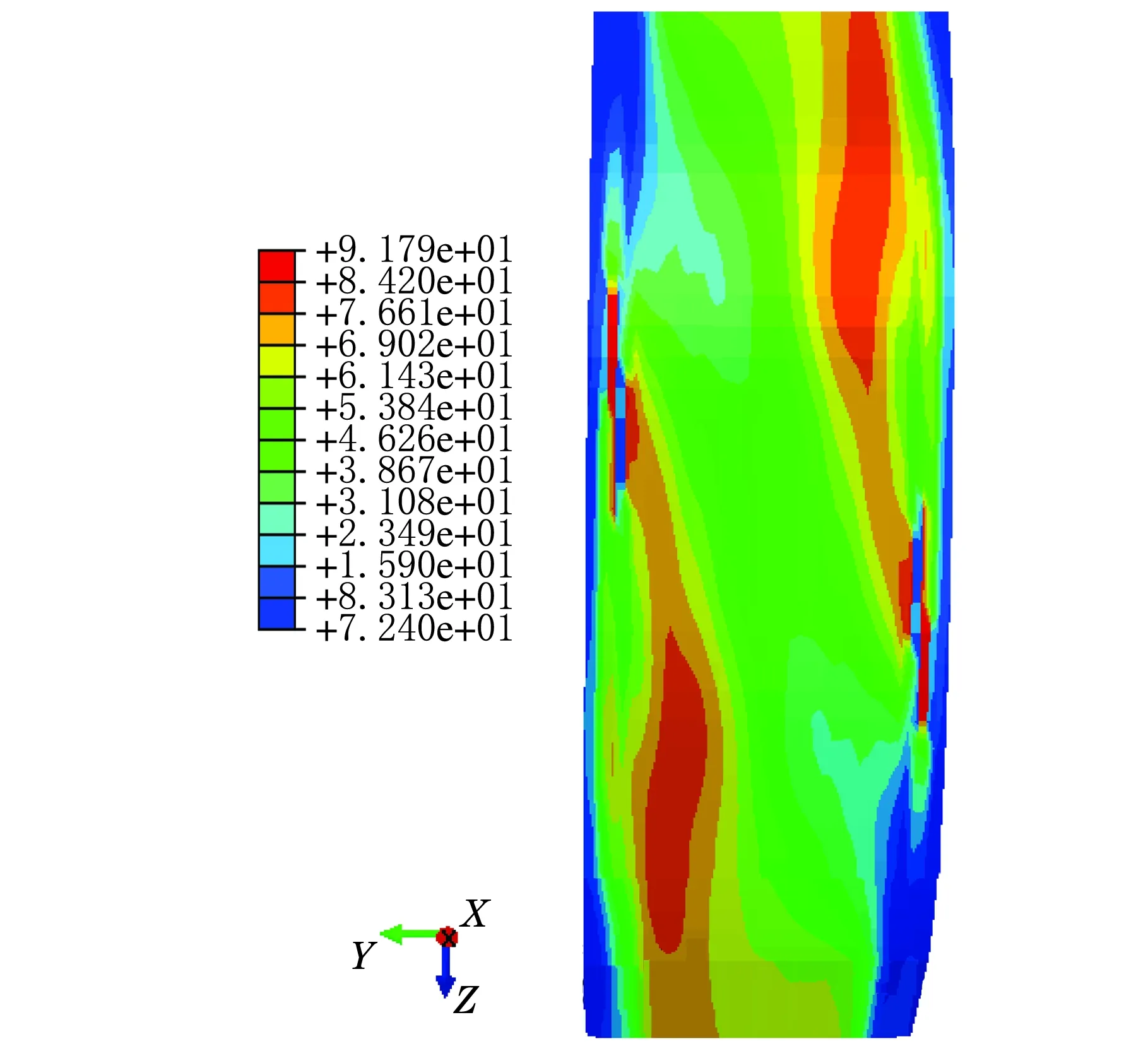
图11 第二层带束层接地处应力图

3.3 带束层帘线径向力分析

利用分析所得的数据，绘制各层带束层接地处帘线受力的分布图，图12和图13分别显示的是在垂直加载时第一带束层、第二带束层与地面接触部位的径向受力分布情况。

从图12和图13可以看出：第一带束层的径向力的最大值在端部，最大值约为142 N，最小值在接地中心位置且径向力值约为60 N，第二带束层的径向力的最大值在胎肩位置且最大值约为85 N，由外侧向内逐步递减，在接地中心位置的径向力值约为42 N，最小值在带束层端部；径向力的这种变化趋势与轮胎接地区域的应力分布情况相似；带束层径向力的分布情况按照中心轴线对称分布；在轮胎接地的中心部位，带束层的径向力分布曲线有一定的折弯，这是由于轮胎在垂直载荷作用下中心区域产生皱曲现象；第一带束层的受力要大于第二带束层。

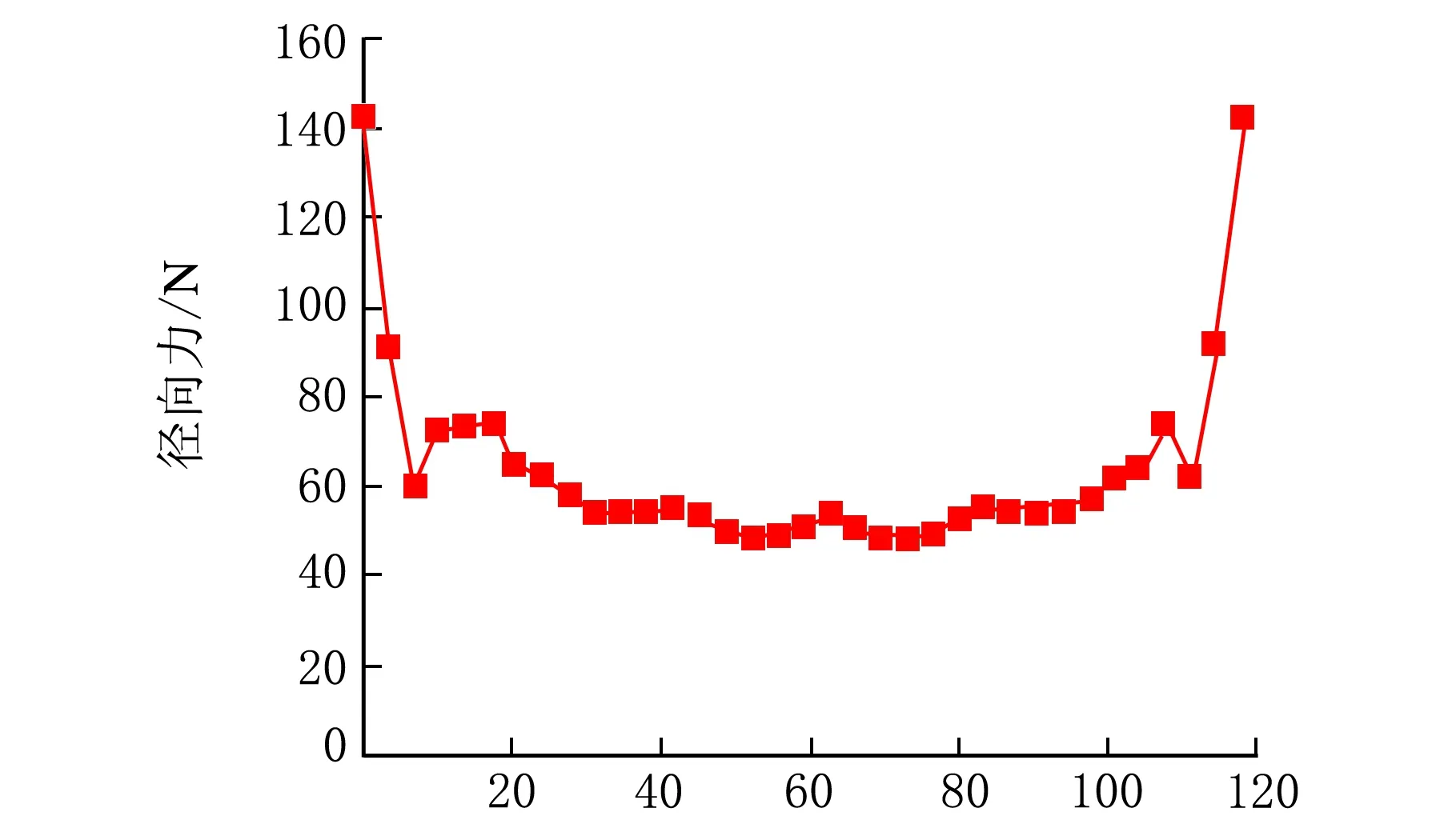
断面宽度/mm图12 第一带束层帘线受力分布图

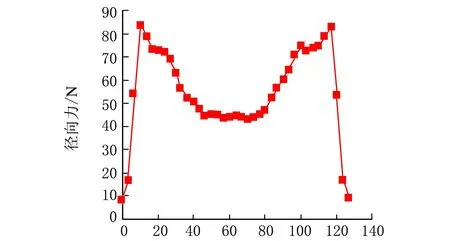
断面宽度/mm图13 第二带束层帘线受力分布图

从图8～图13可得出应力的分布规律及与地面接触部位径向力的最大值与最小值等数据。第一带束层和第二带束层最大受力位置均在胎肩处，这是胎肩部位容易脱空的主要原因之一。从整体上看，分析所得模拟的结果与轮胎实际运行的受力情况比较吻合。

3.4 胎肩部位带束层帘线变形分析

从带束层部位受力的分析可以看出，在胎肩部位受力比较大，故对胎肩部位的带束层帘线进行周向变形分析。本文选取带束层中在胎肩部位的2个点，选取点的位置如图14所示。节点1和节点2分别为第一、第二带束层在胎肩部位上的点。

图14 带束层在胎肩部位分析点的位置

图15是带束层在胎肩部位周向变形图。

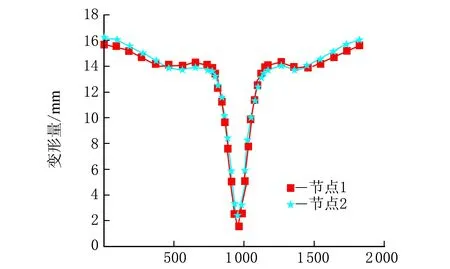
周向弧长/mm图15 带束层胎肩部位周向变形图

从图15可以看出，节点1与节点2的变形趋势及变形量基本上可以看作是相同的；胎肩部位的最大的变形量为16 mm，且发生在带束层与地接触的位置；随着周向长度的增大，胎肩的受力变形逐渐减小，直到距离地面最远距离的位置处，此处的变形量最小；带束层胎肩位置的变形可以看作为关于轮胎轴线对称的图形；在接地端附近周向变形平缓而后急剧减小。

4 结 论

在4 000 N的静载荷和450 kPa充气压力的作用下，对195/65R15子午线轮胎带束层内部进行了以上分析，得出如下结论：

(1) 在轮胎非接地区域，带束层端部的应力值最小，越往内越大，在胎肩部位达到最大值，第一带束层的应力值大于第二带束层。

(2) 在轮胎接地区域，带束层端部应力值最

小，应力值的分布可看作是关于接地中心点的对称图形；第一带束层应力值大于第二带束层。

(3) 从断面内带束层帘线径向力的分布情况可得出，第一带束层和第二带束层的最大值均在胎肩位置，分别为142 N和为85 N，第一带束层的受径向力大于第二带束层。

(4) 从整体上看，第一、第二带束层胎肩处的周向变形趋势及变形量基本上是相同的，钢丝帘线在胎肩部位最大的变形量为16 mm。

分析获得了轮胎骨架材料带束层部位橡胶钢丝复合体的应力分布规律、变形规律，为后续研究中动态加载量和变形量大小的问题提供了数据指导。同时可以根据带束层受力状况，帮助轮胎结构工程师评价带束层的设计方案。

参 考 文 献：

[1] 李丽娟，刘峰，杨学贵，等.子午线轮胎接触变形的非线性有限元分析[J].合成橡胶工业，2000，23(5)：313-316.

[2] 缪红燕，徐鸿，计斌,等.子午线轮胎的有限元分析[J].轮胎工业，2001(1)：16-20.

[3] 王云.橡胶/钢丝粘合强度动态测量理论及方法研究[D].青岛：青岛科技大学，2012.

[4] 赵树高,杨学贵,邓涛,等.子午线轮胎接地问题的三维非线性有限元分析研究[J].轮胎工业,2001,21(11):662-669.

[5] 赵腾伦.ABAQUS6.6在机械工程中的应用[M].北京：中国水利水电出版社，2007.

[6] 徐喆.多工况下子午线轮胎非线性有限元分析[D].青岛：青岛科技大学，2009.

[7] 张翼，唐萌，余美娟,等.胎圈-轮辋接触问题的三维有限元分析[J].轮胎工业，1999，19(2)：83-88.

[8] Koichu Yamagishi,Minora Togashi,Shinichi Furuya.A study on contour of the radial tire:Rolling contour optimization theory-RCOT[J].Tire Science and Technology,1987,15:3-29.