一类三重积分的新算法

段洪玲，刘 日，张玉春

（沈阳理工大学 理学院，沈阳 110159）

0 引 言

在通常情况下，三重积分的计算是通过累次积分进行的，把重积分化为累次积分，确定各次积分限再进行计算，此办法需要计算三次定积分。近几年来，陆续出现了利用monte carlo方法以及利用MATLAB软件去解决三重积分的计算问题［1－4］。最近，又出现了一种新的计算重积分的方法，这种方法是利用概率统计中顺序统计量的数学期望来计算积分的［5－9］。所以，可以引用这种新方法来计算一类三重积分。下面引入顺序统计量，通过一些例子来说明这种方法。

1 主要思想

假设X1，X2，X3是来自区间［0，1］上的均匀分布总体的样本，X1，3≤X2，3≤X3，3为相应的顺序统计量，令＝X1，3，＝X2，3－，＝X3，3－X2，3，根据顺序统计量的性质知，（，）的联合密度函数为f（x）＝3！，所以

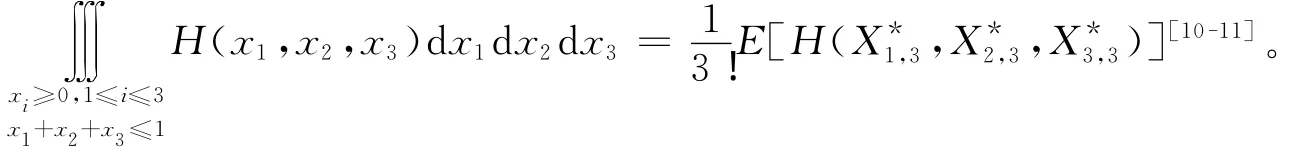
其中E是数学期望。这样，有很多三重积分的计算就可以通过计算顺序统计量的数学期望得到解决了。

2 主要结果

引理1［12］区间［0，1］上的均匀分布的顺序统计量X3，3的概率密度函数是f（x）＝3x2，0≤x≤1

解 可以将三重积分直接改为一重积分，且由引理1可得，

解 方法同上，即

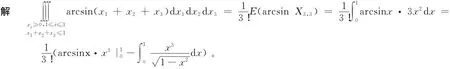
以上例子都是比较简单并且直接利用顺序统计量的数学期望计算出结果的。除此之外，我们还可以进一步利用顺序统计量的条件数学期望去计算较复杂的一些三重积分。

引理2［13］（X1，3，X2，3，X3，3）通过给定X3，3＝x的条件分布等价于（）来自区间［0，x］上均匀分布的无条件分布。即（X1，3，X2，3）（Y1，2X3，3，Y2，2X3，3）其中Y1，Y2独立同分布于区间［0，1］上的均匀分布；同时它们也与X1，X2，X3独立。

此时以X3，3作为条件，对上面等式右端取条件数学期望，利用全期望公式［14－15］及引理2得

由于Y1，2，Y2，2是［0，1］区间上顺序统计量，

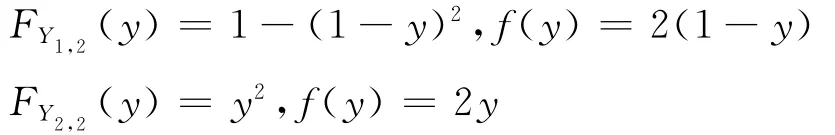
其中0≤y≤1.

所以，

3 结 语

上述方法直接把三重积分计算变为一重积分的计算，省去了原有的复杂计算步骤，过程简洁清晰。像这样利用概率知识去解决高等数学中的某些问题，有时候会得出令人意想不到的效果，这也体现出如今交叉学科之间的互相应用的重要性。

［1］SIVAZLIAN B D.The generalized Dirichlet’s multiple integral［J］.SIAM Rev，1969，11（2）：285－288.

［2］MORREY Jr，CHARLES B.Multiple Integral in the Calculus of Variations［M］.Berlin：Springer－Verlag，2008.

［3］GRUNDMANN A，MOELLER H M.Invariant integration formulas for the n－simplex by combinatorial method［J］.SIAM J Numer Anal，1978，15：282－290.

［4］DAVID H A，NAGARAJA H N.Order Statistics［M］.3ed.Hoboken：John Wiley ＆Sons，2003.

［5］GUMBEL E J.Statistics of Extremes［M］.New York：Columbia University Press，1956.

［6］PEARSON K.Tables of the I－complete Beta Function［M］.London：Cambridge University Press，1934.

［7］SIOTANI.Order statistics for discrete case with a numerical application to the binomial distribution［J］.Ann Inst Stat Math，1956，8：95－104.

［8］GATHER U，KAMPS U，SCHWEITZER N C.Characterization of distributions via identically distributed functions of order statistics［J］.Handbook of Statics，1998，16：257－290.

［9］HAMEDANI G G，VOLKMER H.Certain characterizations of the uniform distribution［J］.Metrika，2005，61：117－125.

［10］ARNOLD B C，BALAKRISHNAN N，NAGARAJA H N.A First Course in Order Statistics［M］.New York：Wiley Press，1992.

［11］SHIMIZU R，HUANG J S.On a characteristic property of the uniform distribution［J］.Ann Inst Statist Math，1983，35：91－94.

［12］茆诗松.概率论与数理统计教程［M］.北京：高等教育出版社，2012：11.

［13］SUN Ping.The application of order statistics to multiple integration over a canonical simplex［J］.Stat Probabil Lett，2012，82（9）：1641－1647.

［14］林元烈.应用随机过程［M］.北京：清华大学出版社，2003：6.

［15］王昕，程希明.概率论与数理统计案例教学方法探析［J］.沈阳师范大学学报：自然科学版，2013，31（3）：372－375.