随机变量间的相互关系与分类

2014-05-16石业娇孟宪涛

沈阳师范大学学报(自然科学版) 2014年2期

石业娇，孟宪涛

（1.大连海洋大学应用技术学院，辽宁大连 116300；2.沈阳师范大学数学与系统科学学院，沈阳 110034）

在概率论中，随机变量的不相关性是由矩阵推出来的概念［1－2］，而随机变量的独立性则是用随机变量的分布加以定义的，虽然随机变量的不相关性与独立性是2个不同的概念［3－6］，但它们之间却存在着一定联系。除不相关性与独立性之外，随机变量之间还存在着诸如相关关系、线性关系等各种关系［7－13］。正确认识深刻理解作为概率论与数理统计的重要工机变量之间的各种关系的内存联系，对深入研究概率与数理统计有关内容是十分必要的。

1 随机变量间的关系

设随机变量X＝X（e），Y＝Y（e）是样本空间S＝｛e｝上的函数。由于样本空间以及X（e），Y（e）的各异，X，Y之间的关系也多有不同。X，Y之间的关系大致有相关、不相关、独立与不独立等各种情况。为理清各种关系的内在联系，需先了解各种关系的概念，为此下面先从介绍相关系数入手。

1.1 相关系数

定义1 若随机变量X和Y的二阶混合中心矩E｛［X－E（x）］［Y－E（x）］｝存在，则称其为随机变量X与Y的协方差，记为coυ（X，Y），即

可以从2个方面解释相关系数ρXY的含义。

第1种解释为随机变量X与Y的标准化随机变量间的协方差。事实上，记

第2种解释，ρXY刻划了随机变量X与Y之间所具有的某种线性关系的紧密程度。事实上可以用线性函数＾Y＝aX＋b来近似表示Y，显然近似程度可用（Y－＾Y）2的均值来表示，即用

来表示。可用对a，b求偏导并令其为零的办法，求出与Y近似程度最好的线性函数＾Y＝a0X＋b0中的相应a0，b0，即由

则＾Y＝a0X＋b0就将满足

易见＾Y＝a0X＋b0完全由X，Y确定，且由式（1）可知，ρXY确定了Y与直线＾Y＝a0X＋b0的靠近程度。换言之，ρXY刻划了X，Y之间所具有的线性相关程度。

1.2 相关关系

定理1 设随机变量X，Y的相关系数为ρXY，则有｜ρXY｜≤1。

为了对随机变量之间关系进行分类，给出如下定义：

定义3 设随机变量X，Y的相关系数为ρXY，则当ρXY≠0时，称X，Y具有相关关系；当ρXY＝0称X，Y不相关。

相关关系又称线性相关关系，由式（1）可见，｜ρXY｜越大，X与Y之间的关系就越接近于线性关系，而当｜ρXY｜越小，X与Y之间的线性相关程度就越差。当ρXY＝0时，称X，Y不相关，是说X与Y之间不存在线性相关关系，但并不是说X与Y之间没有其他的函数关系。下面的例1便可说明这个问题。

Y －1 0 1 P（Y＝j）X 0 0 1／3 0 1／3 1 1／3 0 1／3 2／3 P（X＝i） 1／3 1／3 1／3 1

1.3 线性关系

随机变量间的线性关系有两种，第一种是确定的线性关系。

定义4 设X＝X（e），Y＝Y（e）为定义在样本空间S＝｛e｝上的随机变量，若对任一e∈S，都有Y＝aX＋b（a，b为常数），则称随机变量X，Y具有确定的线性关系。

第二种是随机变量X，Y以概率1存在着线性关系。这种关系由P（Y＝aX＋b）＝1确定，等价描述为

1）Y＝aX＋b依概率1成立；

2）Y＝aX＋b几乎处处成立；

3）P（Y≠aX＋b）＝0；

容易求得E（X）＝0，E（Y）＝

4）Y≠aX＋b只在测度为零的集合上成立。

由式（1）可推得下列定理：

定理2 设随机变量X，Y的相关系数为ρXY，则｜ρXY｜＝1的充要条件是存在常数a，b，使

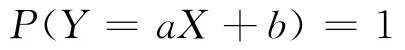
1.4 独立性

定义5 设F（x，y）是二维随机变量（X，Y）的分布函数，FX（x），FY（y）分别为随机变量X，Y的分布函数，若对所有x，y有

则称随机变量X与Y是相互独立；反之，若至少有一对（X，Y）的取值（x，y）使

则称随机变量X与Y不是相互独立的，或称不独立。

需要注意的是，对于连续型随机变量（X，Y）来说，独立性的定义等价形式为

在平面上几乎处处成立。这里f（x，y）为（X，Y）的联合概率密度，fX（x）fY（y）分别为X，Y的概率密度。在独立性定义后一种表述中，已把条件放宽为允许（3）在测度为零的集合上不成立，而前一种表述则要求在（2）全平面上成立。

对于非独立性关系，一般又可分为两种，一种是X、Y之间具有确定的函数关系。非独立性另一种情况则是虽然随机变量X，Y之间具有某种联系，但却不能将这种关系表为随机变量之间的函数表达式形式。

2 独立性与不相关

定理3 若随机变量X，Y相互独立，则X，Y不相关。

定理3的逆命题为假，即由X，Y的不相关，不能推出X，Y是相互独立的。例如在例1中，已求得X，Y是不相关的，但X，Y却不是相互独立的。事实上，由（X，Y）的分布律可见，P（X＝－1，Y＝1）＝

即X，Y不是相互独立的。

值得注意的是，对于下列2种情况，随机变量X，Y的相互独立与X，Y的不相关是等价的：

1）（X，Y）～N（，ρ）；

2）X服从（0－1）分布，Y服从（0－1）分布。

3 随机变量关系图

如果按相关性进行一级分类，可得随机变量之间关系分类如图1。

图1 按相关性优先划分的关系图

4 结语

以上对随机变量之间的关系进行综述，并按相关性作为优先划分指标，将随机变量关系划分如图1关系。从图1中可以清晰地看到随机变量诸多关系的内在联系，正确理解各种关系的条件内涵以及它们之间的逻辑关系有利于深刻理解并全面掌握概率论有关的知识内容［14－16］，对于研究或处理涉及到随机变量之间关系的问题是大有益处的。

［1］盛骤，谢式千，潘承毅.概率论与数理统计［M］.4版.北京：高等教育出版社，2008.

［2］茆诗松，程依明，濮晓龙.概率论与数理统计教程［M］.北京：高等教育出版社，2004.

［3］郭存娣.谈二维随机变量的函数的分布函数［J］.高等数学研究，2003（3）：37－39.

［4］崔瑞峰，牛新军.随机变量相互独立与不相关之间关系的推广［J］.西安电子科技大学学报，1999，26（2）：26－28.

［5］吕洪升，张千祥.二维连续型随机变量相关计算的积分限确定问题［J］.大学数学，2011，27（3）：194－100.

［6］王翠茹，田振清.两随机变量简单相关系数图式的算法设计［J］.中国教育技术装备，2011（06）：69－70.

［7］欧阳敏华.二元随机变量相依关系的图示判别［J］.统计与决策，2012（3）：27－29.

［8］王志祥.不同类型随机变量和差积商的分布［J］.高等数学研究，2010，13（4）：97－99.

［9］彭刚，禹辉煌.二维离散型随机变量独立性判别定理及应用［J］.湖南理工学院学报：自然科学版，2010，23（2）：23－25.

［10］赵海燕，谢成康.连续型随机变量相互独立的密度函数等价条件［J］.大学数学，2011，27（2）：153－155.

［11］崔书英.两个连续型随机变量相互独立判定定理［J］.中国煤炭经济学院学报，1996（4）：85－87.

［12］赵文彬，杨栋辉，郭龙飞，等.二维随机变量独立性的研究［J］.西南民族大学学报：自然科学版，2013，39（4）：543－546.