基于最大似然估计算法实现空气温度分布的可视化

范洪辉， 朱洪锦， 刘晓杰， 田村安孝

（1.江苏理工学院a.计算机工程学院;b.云计算与智能信息处理常州市重点实验室;c.电气信息工程学院，江苏常州 213001;

2.日本山形大学大学院理工学研究科，日本山形县米泽市992-8510）

基于最大似然估计算法实现空气温度分布的可视化

范洪辉1a，b， 朱洪锦1a， 刘晓杰1c， 田村安孝2

（1.江苏理工学院a.计算机工程学院;b.云计算与智能信息处理常州市重点实验室;c.电气信息工程学院，江苏常州 213001;

2.日本山形大学大学院理工学研究科，日本山形县米泽市992-8510）

针对空气中温度差值难以捕捉的问题，以空气中温度分布的可视化作为研究对象，采用基于最大事后概率的最大似然估计算法，研究空气中温度分布图像化问题。可视化测量系统中，在被测区域设置32个收发分离的超声波换能器，基于一发多收模式实现渡越超声信号数据采集，通过实验获取16×16=256个渡越时间参数TOF(Time of Flight)。实验系统采用测量角度插补与渡越时间参数平行插补两种方法进一步补充成像所需渡越时间参数，确保重建图像可读性。对实验数据进行了基于最大似然估计算法的超声波CT图像重建，重建图像结果能成功分辨空气场温度值差异。实验结果表明，基于最大似然估计算法实现空气中温度差异可视化的有效性。

最大似然估计算法;最大事后概率;空气温度可视化;数据插补

0 引言

超声波测温为非接触式测温中的超声波测温技术，因在安全性、实时性、经济性和抗干扰性等方面有较好的综合评价，所以在火箭发射、等离子体室、核反应堆和惰性气体高温测量中都得到了广泛应用［1-2］。目前的超声波测温技术，大多数研究都是利用声速基于温度的变化原理检测被测物体的温度数值，这些研究中的被测对象的温度大多在1 000 K以上，故目前超声测温大多数应用于在高温且较为恶劣的测温环境中［3-4］。

基于超声的图像重建算法主要有解析法和迭代法。解析法的主要代表算法有滤波反投影法(Filtered Back Projection，FBP)，FBP法已经在超声波CT图像中得到广泛应用［5］，虽然FBP法有着计算过程简单，图像重建速度快等优点，但其缺点是重建图像领域数值不能保证全部为真，而且不能有效地抑制噪声影响，所以会在重建的图像上产生许多星状伪影，大大降低重建图像的可读性［6-7］。最大似然期望值算法已经成功应用于医疗超声波CT，近几年，基于最大似然期望值的图像重建算法已被逐渐用于工业的数据可视化计算与工业用超声波CT［8］，与FBP法相比，其优点是在图像重建时能逐渐收敛并且在测量数据不足时也能正常对测量范围进行图像重建，在信息量不足的情况下获得分辨率和噪声特性均优于滤波反投影法的重建结果［9-10］，还能防止在图像重建过程中发生散乱现象，保证最后收敛到一个概率分布的最大似然值，得到效果更好的重建图像［11-12］。

根据超声波在空气中的传播速度会因空气中温度的变化而变化，本文提出基于最大似然估计与最大事后概率利用超声波的渡越时间参数实现空气温度分布的可视化，将普通空气温度差异作为测量对象，研究空气中局部温度变化的可视化。实验采用全域渡越时间测量方法获取渡越时间参数(Time of Flight，TOF)［13-15］，基于穿越被测空气场内的超声信号，对被测空气温度场进行超声波CT的图像重建，从而实现空气中温度分布的图像化。

1 基于最大事后概率的最大似然估计

最大似然估计基于数据的概率统计特性，利用系统的固有分辨率，实现重建图像分辨率和噪声特性均优于卷积反投影的重建结果。在超声波成像系统中，最大似然模型是建立在从渡越时间参数推算路径超声音速分布的基础上实现图像重建。如图1所示，假定被测区域设置N个检测器，检测器处检测的概率为C，λ为断层画像上像素浓度，x为投影数据上像素j的计数，则像素j浓度λ的最佳推算值由下式计算:

但x为实际检测过程没有的假定对象，故引入最大事后概率MAP(Maximum a Posteriori)，y为投影方向上各像素的实际投影数据，则基于最大事后概率原理x的MAP推定值如下式所示:

故假定投影数据上像素的计数x可通过像素浓度λ与投影数据计数得出。

将式(2)代入式(1)，整理后可得到基于投影数据进行图像重建的最大事后概率的最大似然估计:

本实验系统中，利用超声的渡越时间参数进行图像重建，式中各参数具体意义如下:i为投影数据上的画素标;j为断层图像上各画素标;λj为画素j的音速的倒数;yi为第i个TOF;Cij为画素j在i处的检出率;k为收敛最终参数。

图1 像素j投影数据示意图

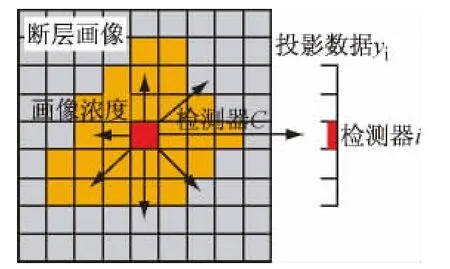
图2 基于MAP原理像素j投影数据示意图

TOF数据i基于预测面积比例记述像素j。覆盖所有面积时Cij=1.0。计算过程中基于微小间隔对传送路径进行扫描，基于下式计算路径上个点的相邻像素j所对应的Cij:

其中:(x，y)为传送路径上点的坐标;(xj，yi)为像素j的坐标。

图像重建的具体计算流程为:

①首先计算初期检出率Cij。

②用平均数值设定初期图像λ0。

③对测定数据的像素的反投影进行计算。

④对像素j处第i个测定数据的投影进行计算。

⑤计算步骤③、④中所有角度的投影，对比较后数据进行相加计算。

⑥检出率Cij规格化。

⑦得到的计算值与初期图像的像素j相乘后得到画素j的重建图像的像素。

⑧j+1处的画素计算从步骤③开始重新计算。

⑨首枚图像所有的像素值计算完成后，重建图像更新为初期图像从步骤③开始重新计算。

利用以上的计算方式循环计算，可计算出逐渐收敛的重建图像，通过引入图像的先验分布约束，从而提高重建图像的分辨率、噪声性能并进一步提高图像重建的质量。

2 基于TOF的空气场温度可视化实验

2.1 实验系统

TOF超声波CT是基于超声波在其传播路径的音速分布实现重建图像，为更好地重建被测空气场的CT图像，在实验系统中采用全域测量的方法获取分布合理的TOF，实验系统概略图如图3所示。系统中，计算机用于超声波信号发送和接收的控制，并兼备对实验数据进行计算。

图3 实验系统概略图

在被测区域周边均匀间隔设置32个信号发送和接收换能器。其中超声波信号发生换能器Transmitter(见图4)和超声波信号接收换能器Receiver(见图5)互相间隔设置。Transmitter直径为12 mm，中心频率为46.6 kHz。Receiver具有较宽的波率频段，为便于信号的高精度接收，其构造结构采用弯曲构造。实验系统中用信号增幅器将信号增大由发送换能器发射超声信号，超声波信号接收换能器经转换及前置放大后用数字示波器对其进行检测接收后将实验数据存于计算机，计算机对数据计算成像后将结果发送到显示屏。

图4 发送信号用换能器

图5 接收信号用换能器

图6为本实验系统所设定的测量范围实景图，为直径55 cm的圆形空气温度场。

图6 TOF测定装置

2.2 空气场温度设定

为保证测量领域内的空气场温度差值的可靠性，本实验中采用日本后藤工艺会社定制的温度发生器(见图7)，它由加热器和温度控制器两部分构成。在温度器部分覆有5 cm的钢化玻璃罩，其作用是在温度数值被设定后，确保温度变化过程中加热点与被周围空气不发生对流现象，从而提高温度设定点与测量范围内温度差值精度。

图7 温度设定仪器

2.3 TOF 测量

为保证重建画像能够准确地显现出被测区域空气温度分布，实验系统要求测量路径尽可能全面覆盖被区域。本文测量方式如图8所示，在所设置测量点处，按照信号发送端顺序逐点间隔测量(图8中所示测量路径实线为 Transmitter1所测路径;虚线为Transmitter2所测量路径)。所用16个发送端全部测量完成后，得到16×16=256个TOF。

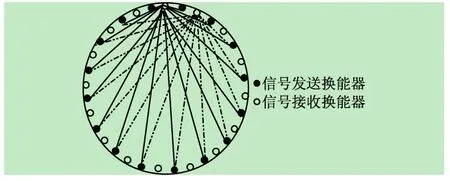
图8 TOF测量示意图

因为基于最大似然期待值最大算法进行图像重建时，需要大量数据对波形图进行数据处理计算，23℃和25℃的通过中心点的测量路径的渡越时间参数为0.001 851 s和 0.001 812 s，但在此处的理论传播时间为0.001 591 s和 0.001 598 s。在实验中所测得的TOF数据值比理论数据值大，这是因为在对测得的波形进行分析时，由于噪声信号的影响，读取接收信号开始的位置稍微偏前的原因。

对所有测得TOF数据整理后，利用最大似然估计算法对所测空气的温度场进行CT图像重建，图9为实验结果图。当测量区域温度全域为20℃时，重建图像内部亮度均一;当中心温度设定为23℃时，重建图像中心部亮度变化不明显，这是由于中心部与周围温度差值较小，所测渡越时间参数变化不大的原因。当中心部温度逐次提高(设定为25℃、30℃)，从实验结果中可以看出，重建图像中心部位亮度逐渐增强，在中心温度有跳跃性变化(设定为40℃)时，CT重建图像中心区域亮度也表现出跳跃性增强。测试区域中心部温度升高，超声波CT重建图像中心部亮度也随之对应变化，所以基于最大似然期望值算法来实现空气中温度分布图像化得到验证。

图9 图像重建结果图

为保证基于渡越时间参数重建图像的准确性以及进一步提高重建图像的图像质量，用图10所示的角度插补法与平行插补法来增加TOF的数量。基于发送端实施角度插补后测量路径变为(16×2)×(16×2)=1 024，在角度插补基础上再进行数据平行插补后可以最终得到1 024×2=2 048个TOF。

图10 TOF数据插补示意图

3 实验结果与讨论

为保证实验过程中测量精度，实验室空间温度用空调设定为恒温20℃，进行一次测量，然后在圆中心直径5 cm范围内的设定温度依次发生变化(23℃，25℃，30℃，40℃)，记录每次温度变化时所测波形。为降低测量误差及噪声的影响，每个温度数值被设定后进行3次测量，最后取其TOF的平均值。图11的波形图是中心温度为23℃和25℃时直径路径上的接收信号波形图。

图12为20℃和40℃重建图像所对应的音速分布图。图中表明，20℃重建温度场内音速分布均匀;40℃的音速分布图中心音速明显高于周围音速，进一步验证了实验结果的准确性。

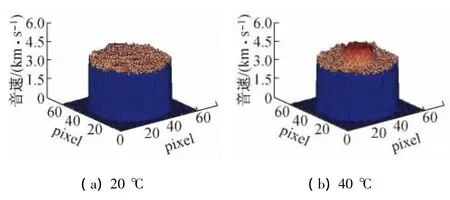
图12 重建图像音速分布示意图

4 结语

本文的目的是验证基于最大似然估计与最大事后概率法的空气温度的超声波CT。通过实验结果可知，利用超声波传播速度随温度变化而变化这一特性，通过全域测量被测空气场的渡越时间参数，基于最大似然估计算法可以实现空气中温度变化差异的可视化。但由于噪声信号影响，还不能达到亮度值与温度值的准确对应。且基于最大似然估计算法的在图像重建过程中需要更精准的持续收敛，因此如何提高收敛速度也是下一步需要解决的问题。

［1］ 张华宇，谢凤芹，李 强.超声波在空气温度场重建中的应用［J］.山东科技大学学报(自然科学版)，2012，31(1):94-98.

ZHANG Hua-yu，XIE Feng-qin，LI Qiang.Application of ultrasonic wave technique in reconstruction of air temperature field［J］.Journal of Shandong University ofScience and Technology(Natural Science)，2012，31(1):94-98.

［2］ 王 琪，王利军，田 亮.为随机码超声扩频在声学测温中的应用研究［J］.仪表技术与传感器，2012，31(12):88-90.

WANG Qi，WANF Li-jun， TIAN Liang. Research of acoustic pyrometry employing pseudo-random sequence ultrasonic spread spectrum［J］.Instrument Technique and Sensor，2012，31(12):88-90.

［3］ 王利军，天 亮，叶 艳，等.超声波温度测量装置的设计与实现［J］.电站系统工程，2011，27(6):19-25.

WANG Li-jun，TIAN Liang，YE Yan，et al.Design and implement of an ultrasonic temperature measurement device［J］.Power System Engineering，2011，27(6):19-25.

［4］ 米小兵，张淑仪，张俊杰，等.超声波自动测温计算技术［J］.南京大学学报(自然科学版)，2003，39(4):517-524.

MI Xiao-bing，ZHANF Shu-yi，ZHANG Jun-jie，et al.Automatic ultrasonic thermometry［J］.Journal of Nanjing University(Natural Science)，2003，39(4):517-524.

［5］ 马 敏，赵 亮，姬晶晶.基于Wiener滤波的反投影图像重建算法［J］.核技术，2012，35(9):675-679.

MA Min，ZHAO Liang，JI Jing-jing.A wiener filtering back projection algorithm for image reconstruction［J］. Nuclear Techniques，2012，35(9):675-679.

［6］ 张顺利，李卫斌，唐高峰.滤波反投影图像重建算法研究［J］.咸阳师范学院学报，2008，23(4):47-49.

ZHANG Shun-li，LI Wei-bin，TANG Gao-feng.Study on filtered back projection algorithm of image reconstruction［J］.Journal of Xianyang Normal University，2008，23(4):47-49.

［7］ 马晨欣，胡君杰，闫 镔.CT扇形束滤波反投影图像重建算法优化［J］.激光与光电子学进展，2012，49(9):091103.

MA Chen-xin，HU Jun-jie，YAN Bin.Optimization of Fan-Beam CT filtered back projection reconstruction Algorithm［J］.Laser＆Optoelectronics Progres，2012，49(9):091103.

［8］ 谢勤彬，罗代升，宋海波.基于改进各向异性扩散的超声医学图像滤波方法［J］.电子技术应用，2008(2):123-125.

XIE Qin-bin，LUO Dai-sheng，SONF Hai-bo.A medical ultrasound image filtering method based on improved anisotropic diffusion［J］.Computer Technology and Its Applications，2008(2):123-125.

［9］ Fan Hong-hui，Yanagida H，Tamura Y，et al.Image quality improvement of ultrasonic computed tomography on the basis of maximum likelihood expectation maximization algorithm considering anisotropic acoustic property and time of flight interpolation［J］.Japanese Journal of Applied Physics，2010，49:07HC12.

［10］ 杨亚良，周振明，丁志华.光学投影层析的快速图像重建和影响因素分析［J］.光子学报，2008，37(7):1488-1491.

YANG Ya-liang， ZHOU Zhen-ming， DING Zhi-hua. Rapid implementation of filtered back-projection and analysis of influencing factors on image reconstruction in optical projection tomography［J］.ACTA Photonica Sinica，2008，37(7):1488-1491.

［11］ Keiichi Matsumoto，Toru Fujita，Koji Oogari.Evaluation of median filtering after reconstruction with maximum likelihood expectation maximization(ML-EM)by real space and frequency space［J］.Jappan Journal of Radiological Technology，2002，58(5):670-678.

［12］ 张华宇，谢凤芹，李 强.块修正插值计算在超声波温度场测量中的应用［J］.传感器与微系统，2012，31(4):146-148.

ZHANG Hua-yu，XIE Feng-qin，LI Qiang.Application of the block correction interpolation technology in ultrasonic wave temperature field measurement［J］.Transducer and Microsystem Technologies，2012，31(4):146-148.

［13］ 范洪辉，朱洪锦，柳田裕隆，等.超声波信号渡越时间参数法测量空气中温度分布［J］.应用声学，2010，29(1):53-57.

FAN Hong-hui， ZHU Hong-jin， HirotakaYanagida，etal.Measurement of air temperature distribution based on ultrasonic time of flight［J］.Applied Acoustics，2010，29(1):53-57.

［14］ 赵正敏，李洪海.超声波TOF的递推相关估计［J］.仪器仪表学报，2010，31(12):2689-2694.

ZHAO Zheng-min， LI Hong-hai. Recursive cross-correlation estimation of ultrasound TOF［J］，Chinese Journal of Scientific Instrument，2010，31(12):2689-2694.

［15］ 王雪峰，唐祯安.基于自干涉驱动技术的超声波飞行时间测量系统优化设计［J］.传感技术学报，2010，23(10):1439-1443.

WANG Xue-feng，TANG Zhen-an.Optimization on ultrasonic timeof-flight measurement system based on self-Interference driving technology［J］.Chinese Journal of Sensors and Actuators.2010，23(10):1439-1443.

Graphical Distribution of Air Temperature Based on Maximum Likelihood Algorithm

FAN Hong-hui1a，b，ZHU Hong-jin1a，LIU Xiao-jie1c，TAMURA Yasutaka2

（1a.College of Computer Engineering;1b.Key Laboratory of Cloud Computing ＆ Intelligent Information Processing of Changzhou;1c.Department of Electrical Engineering，Jiangsu University of Technology，Changzhou 213001，China;

2.Graduate School of Science and Engineering，Yamagata University，Yonezawai Yamagata 992-8510，Japan）

This research aims to at evaluate evaluating the temperature distribution in the air using an ultrasonic computed tomography imaging technique.The Maximum likelihood algorithm was is applied to ultrasonic time of flight(TOF)computed tomography(CT)for temperature distribution in the air based on maximum a posteriori.32 ultrasonic transducers(receive and transmission function separation)are set in measure area，ultrasonic signal which transits measure area with temperature difference is collected based on TOF，so we get 16×16=256 TOF.Ultrasonic CT images are reconstructed by using the measured data，temperature differences in the air can successfully distinguish in the reconstructed image.Experimental results show that the Maximum likelihood expectation maximization algorithm for air temperature image reconstruction effectiveness.

maximum likelihood;maximum a posteriori;air temperature visualization;time of flight interpolation

TB 559

A

1006－7167(2014)05－0012－05

2013－07－06

国家自然科学基金项目(61302124，11274091);江苏省自然科学基金项目(BK20130235);江苏省高校自然科学基金项目(13KJB520006，12KJD510005);常州市云计算与智能信息处理重点实验室项目(CM20123004);江苏省“六大人才高峰”资助项目(DZXX-031)

范洪辉(1980－)，男，山东诸城人，博士，副教授，主要研究方向为图像重建，机器视觉。

Tel.:0519-86953252;E-mail:fanhonghui@jsut.edu.cn