线性回归方程式在检测煤胶质层中的应用

郑 威

（天津天铁冶金集团技术中心，河北涉县 056404）

线性回归方程式在检测煤胶质层中的应用

郑 威

（天津天铁冶金集团技术中心，河北涉县 056404）

应用线性回归方程测量煤的胶质层最大厚度值与粘结指数值之间相关关系。根据实际数据判断两者的强相关性，求得线性方程，用显著性方法检验了线性方程的成立。通过对线性回归方程的标准误差的概率值，证明胶质层最大厚度估算值具有较强的准确性。该方程可应用与煤胶质层测定过程，以及炼焦工艺快速配煤Y值的估算与异常Y值的辨别中。

线性回归方程式；煤；胶质层；粘结指数；相关性；检测

1 引言

煤的粘结指数是判别煤的粘结性和结焦性的关键指标，其测定方便、快速、准确度高，在配煤过程中起到重要的指导作用。煤的胶质层指数是鉴定炼焦用煤结焦性和确定煤牌号的重要指标,具有取样多、代表性强、测定后可供参考性多等优点，但其测定周期长，数据准确度相对较低等因素在一定程度上制约了生产的顺利进行。为了能够快速、准确了解煤的胶质层指标,我们着力寻找粘结指数与胶质层最大厚度的相关关系,从而由粘结指数测定值推出胶质层最大厚度值，并运用相关关系对分析结果进行预测。

2 线性回归方程的确立及关系验证

2.1 线性方程的确立

对2013年11月、12月天铁炼焦工艺煤测定的胶质层最大厚度值Y和粘结指数值G的50组数据进行整理。统计结果见表1。

由表1建立胶质层最大厚度（Y）与粘结指数（G）测定值的散点图，见图1。

表1 煤样胶质层最大厚度（Y）与粘结指数（G）测定值统计

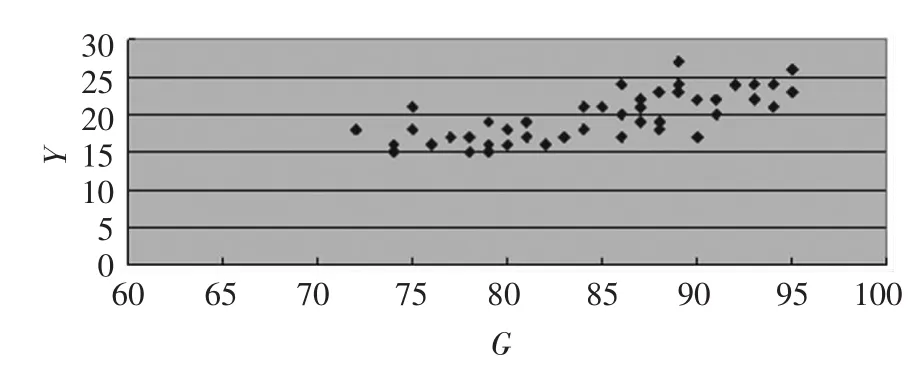
图1 胶质层最大厚度Y值与粘结指数G值的散点图

通过表1数据变化和散点图的点群分布，可以初步判定出胶质层最大厚度Y值与粘结指数G值呈线性关系，求得相关系数r，见公式（1）：

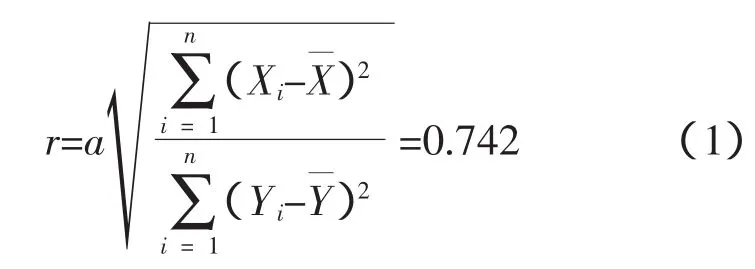
由相关性r可以判定胶质层最大厚度Y值与粘结指数G值呈线性关系，且为强相关（一般r＞0.7为强相关）。其线性回归方程式，见公式（2）：

式中：Ye为胶质层最大厚度的估算值；X为粘结指数的实际测定值。

根据表1数据得出a、b的方程组见公式（3）、公式（4）：

解得 a=0.37，b=－11.6，代入公式（1），得公式（5）：

2.2 线性关系的显著性检验

通过方差分析（即F检验法）的方法对回归方程进行了检验，结果表明,在显著性水平α=0.05水平上方程是有意义的。该回归方程在实际工作中可用于预测胶质层最大厚度。

2.3 实验估算数据的准确度

由于Ye是估算值，它与实际测定值Y存在一定的误差，根据所得线性回归方程和表1中的G值算出对应的Ye值，整理成表2。根据表2的数据可得出标准估算误差值，见公式（6）：

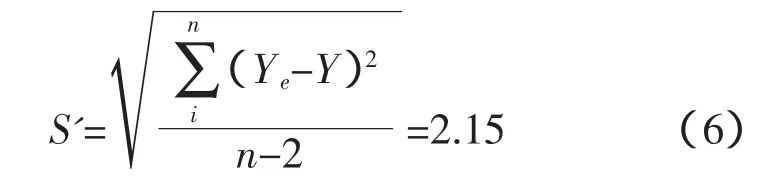
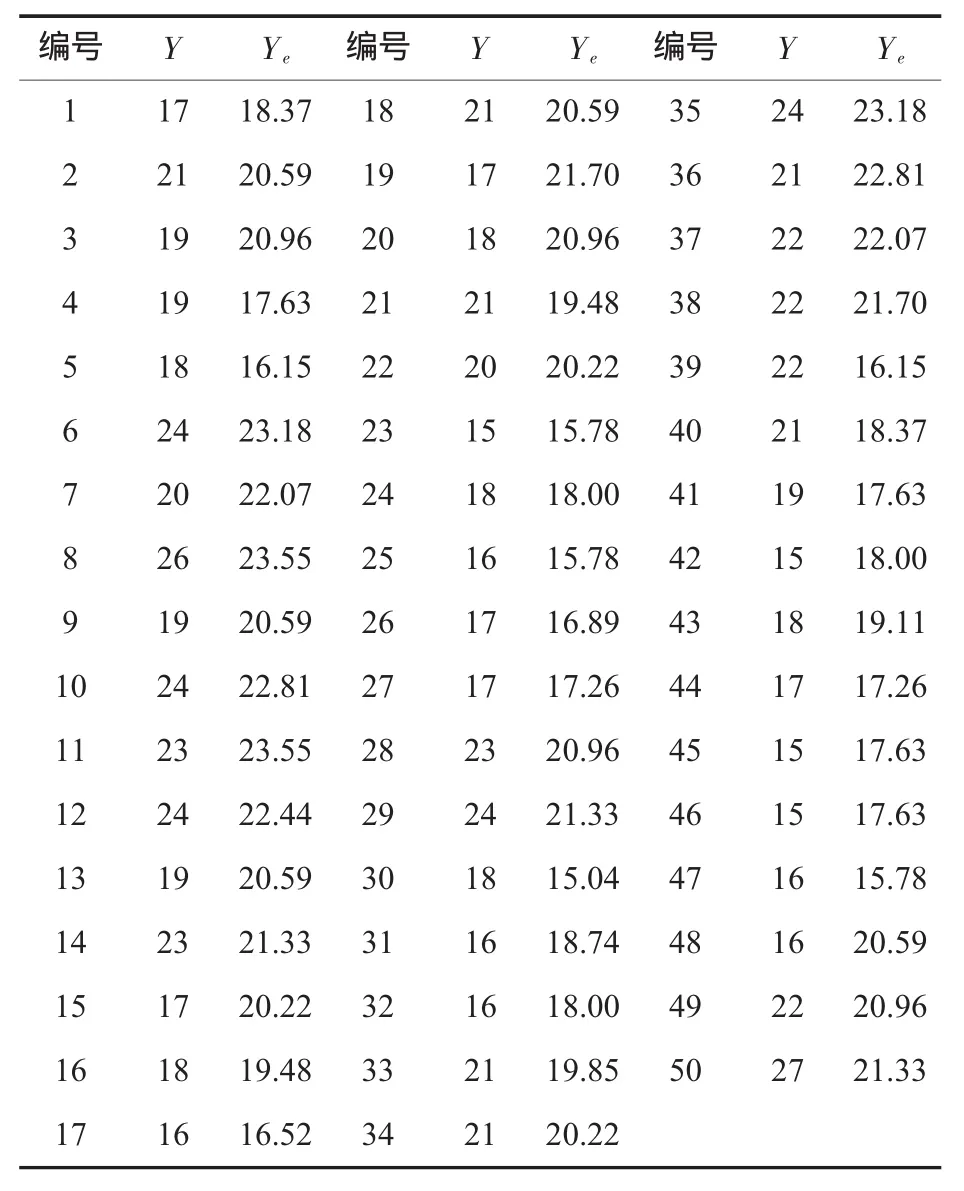
表2 胶质层最大厚度的实际测定值与线性回归方差估算值对比

式中：S'为标准估算误差值；Ye为方程估算值；Y为实际测定值。通过线性区间概率的换算，可知Ye落在Ye=0.37X-9.45和Ye=0.37X-13.75之间的概率为64.3%，落在Ye=0.37X-7.29和Ye=0.37X-15.9之间的概率为99.1%。由标准误差值和概率值可知，胶质层最大厚度估算值的准确性和可靠性都很好，所以该回归方程可用于实际工作中胶质层最大值厚度的预测。

3 线性回归方程在实际工作中的应用

3.1 在煤胶质层检测中的应用

3.1.1 可预测胶质层最大值的测定结果

由于天铁炼焦用煤所测定的胶质层最大厚度的范围集中在15～28 mm，所求得的线性回归方程是用于Y值在15～28 mm的煤样。确立线性回归方程，通过G值计算出煤样的胶质层最大厚度的理论值，再与实际测定值进行对比，便于发现测定的异常值。

3.1.2 线性回归方程在配煤生产中的应用

粘结指数的测定的操作时间大约在30min，而且设备简单，单次可测得多个试样，而胶质层的测定周期较长，一般在2 h左右，每次只能测定一个煤样，且要进行平行测定。在配煤生产中应用线性方程，可快速地估算出胶质层的最大厚度值，快速、准确地了解煤的胶质层指标，提高了炼焦配煤的速度，为配煤生产提供了快速、准确的数据支持。

3.2 应用过程中存在的问题

3.2.1 线性方程在应用中的时效性

为了明确该线性回归方程应用时间的有效期，重新抽取了2013年1月份天铁炼焦工艺煤测定的20组数据，将该组数据的G值利用所求得的线性回归方程计算，得到胶质层最大厚度的估算值Ye，并与实际测得的胶质层最大厚度值Y相比较，见表3。

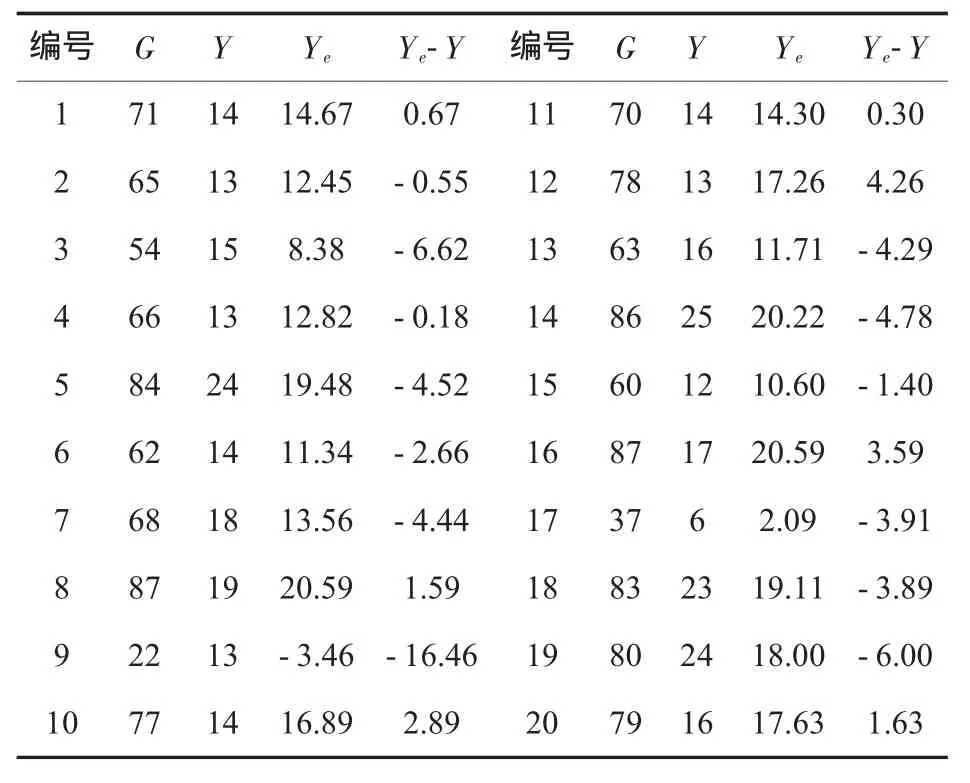
表3 胶质层最大厚度的实际测定值与线性回归方差估算值对比

求得该组数据的误差，见公式（7）：

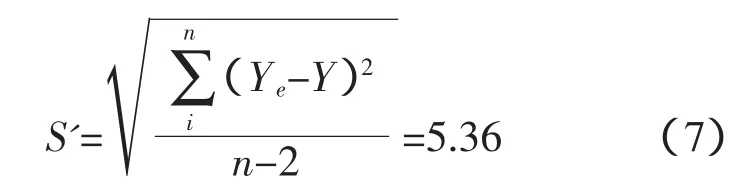
由表3中的数据和误差值可以看出，该组数据的误差较大，估算值的准确性较差；估算值与实际测定值的偏离值（Ye-Y）的范围较大。即该组数据不适合用此线性方程估算，需重新确立线性方程。说明了分析煤样胶质层最大厚度（Y）与粘结指数（G）的线性方程具有一定的时效性。根据2013年全年天铁炼焦工艺煤胶质层测定的数据对比分析，在天铁进场煤来源稳定的情况下，线性方程的有效时间一般为2～3个月。

3.2.2 挥发分的影响

在查阅煤的相关资料后，发现煤的挥发分对胶质层最大厚度与粘结指数的相关性有一定的影响，见表4。若按照不同的挥发分再次拟合后，胶质层最大厚度与粘结指数的相关性也会更强，建立的相关性方程的准确度更高。但考虑到影响实验条件的不稳定因素相对较多和计算相对繁琐复杂，挥发分对估测值准确性的影响较小，所以在本文中可忽略挥发分对估算值Ye的影响。

表4 煤的胶质层最大值、粘结指数及挥发分区间的关系统计值

4 结论

通过对天铁炼焦煤的胶质层与粘结指数数据的分析，确立了两者的强相关性，求出线性回归方程并通过显著性验证方程成立，该线性方程估算Y值的准确度高，并将该线性方程应用于胶质层最大厚度范围在15～28 mm之间的胶质层测定中的异常值辨别和配煤生产中Y值的快速估算，便于在实际工作中快速、准确的了解煤的胶质层指标。

[1] 吴红萍.胶质层最大厚度与粘结指数的线性关系及其应用[J].煤炭技术，2002（1）：24-25.

[2] 刘仙平，陈桃花.用煤的挥发分、胶质层厚度计算煤的粘结指数[J].中国煤田地质，2002（2）：20-22.

Application of Linear Regression Equation to Coal Gelatinous Layer Detection

ZHENG Wei

(Technology Center of Tianjin Tiantie Metallurgical Group,She County,Hebei Province056404,China)

Linear regression equation is utilized to determine the relationship between the maximal thickness and cohesion index of coal gelatinous layer.Their strong correlation is judged based on actual data to solve linear equation and significance method tests the establishment of linear equation.The probability value of linear regression equation standard error proves that the estimated maximal thickness value of gelatinous layer is quite accurate.This equation can be applied to the determination process of coal plastic layer and Y

value estimation and abnormal Y value differentiation at fast coal blending in coking process.

linear regression equation;coal;gelatinous layer;cohesion index;correlation;detection

10.3969/j.issn.1006-110X.2014.03.020

2014-01-03

2014-01-27

郑威（1986—），女，主要从事煤焦分析技术管理工作。