完整岩体对测井频率应力波的滤波特性

王观石，胡世丽，2，李志文，王星光

（1．江西理工大学，赣州 341000；2．中国地质大学，北京 10083）

完整岩体对测井频率应力波的滤波特性

王观石1，胡世丽1，2，李志文1，王星光1

（1．江西理工大学，赣州 341000；2．中国地质大学，北京 10083）

不同频率范围内的应力波在岩体的传播过程中，衰减系数对频率的依赖性具有显著差异。通过现场试验研究完整岩体对测井频率范围内应力波的滤波特性，针对常用黏弹性模型在描述衰减系数与频率关系存在不足，在频域上对黏性系数进行非定常处理，建立黏性系数非定常Maxwell模型，采用波形相关系数评价改进模型的滤波效果。研究结果表明，完整岩体总体上表现为低通滤波，在低通滤波范围内具有非等间距带通滤波特性，随传播距离增加，带通数逐渐减小；在吸收频率过渡带，应力波衰减系数随频率变化非常快，黏性系数非定常Maxwell模型能够有效描述应力波在完整岩体中的衰减系数变化规律；吸收频率过渡带的边界频率与传播距离成负指数关系，吸收频率过渡带的陡度参数可以近似认为是常数；随传播距离增加，黏性系数非定常Maxwell模型描述完整岩体的滤波效果明显提高，当传播距离为4．75 m时，波形相关系数达到0．89，表明采用改进模型描述完整岩体是有效的。

完整岩体；滤波特性；Maxwell模型；应力波；衰减系数

应力波在黏弹性介质的传播过程中发生衰减，导致记录的应力波信号频带变窄和主频降低，严重影响应力波记录的分辨能力。由于实际岩体是黏弹性的，所以应力波在其中传播时引起速度频散和衰减现象是普遍存在的，只是不同岩体速度频散和衰减程度有所差异，因而，准确描述应力波衰减系数与频率的关系是研究应力波传播规律和地震勘探的重要工作。

岩体是由弹性固体骨架、刚性孔隙、柔性裂缝和黏性流体组成的多相黏弹性介质，介质的应力波传播特性表现为速度和衰减对频率具有不同程度的依赖关系。应力波在岩体的传播过程中，总体上表现出衰减和速度随着频率增加而变大的特征，但不同频带范围内，其变化特征不同［1］。对于P波而言，频散最严重的频段，衰减也趋于最强烈，频散一般表现为速度随频率增加而增加，但是衰减不一定具有这种必然关系［2］。从定性的角度来讲，一般可以划分为低频段（101～102Hz）的低频散低衰减区、高频段（＞105Hz）的低频散低衰减区和中间过渡频段（103～104Hz）的高频散高衰减区。实验观测数据表明，在地震频带范围内，岩体的品质因子随波的频率基本上没有变化，因此通常可以认为是常数。测井频率（103～104Hz）和地面地震频率（101～102Hz）存在不可忽略的速度频散和衰减差异现象，因而导致两个问题在提取子波、参数测试和合成记录等工作中表现出无法完全匹配。在实际数据处理过程中，为达到合成记录与原始地震资料一致的效果，需利用零偏移VPS资料对地面地震资料进行标定，但VPS测量的代价很高，因而仅在油田的重点区块才能采用该方法，或者采取拉伸测井曲线的做法，但需对两个频率范围的速度频散和衰减差异开展进一步研究［3］。

标准Kelvin模型、Maxwell模型和三参数标准固体等黏弹性模型具有物理意义明确，并且能揭示介质的一些主要力学特性，因而得到广泛应用，但是随着人们对介质的力学特性的进一步认识，发现了标准黏弹性模型在描述介质品质因子对频率的依赖关系方面存在不足，与实际观测结果不符，特别是在测井频率范围内［4］。为此开展了大量的研究，对标准模型进行了改进，发展为相应的广义模型［5－6］，提出了非线性黏弹塑性流变模型［7］，非定常Burgers模型［8］，分数Kelvin模型［9］，非定常参数的黏弹性模型［10］等。对于岩石，通常可以描述为Kelvin介质模型［11］，而广义Maxwell模型与广义Kelvin模型具有等效性［12］。如果从应力波传播规律角度考虑介质的黏弹性，目前主要关心的是黏性引起频散和振幅衰减两个方面，其本质是速度和衰减系数与频率的依赖关系。由于存在频散和振幅衰减，导致应力波在传播过程中发生波形变化，声时、波幅和频率仅从某些方面揭示了应力波传播规律，而波形能够综合反映应力波传播规律［13］。理论和试验研究表明子波波形变化比走时对断层的反应更为敏感，充分反映了波形变化规律在岩体力学参数测试和岩体结构探测方面的优势，因而开展应力波波形变化规律的研究具有广阔的应用前景［14］。

概括地说，标准黏弹性模型在反映波速和振幅衰减系数与频率的关系方面存在不足，需要对标准模型的参数进行非定常或非线性改进，而波形变化能够综合反映应力波的传播规律，本文通过对Maxwell模型进行黏性系数非定常改进，采用波形相关系数综合量化应力波波形变化规律，现场试验研究测井频率范围内完整岩体的滤波特性。

1 黏性系数非定常Maxwell模型

应力波在一维标准Maxwell介质中传播时，其控制方程为［15］：

式中u，ρ，t，E，x和η分别为位移、密度、时间、弹性模量、传播距离和黏性系数。标准Maxwell介质反映了黏性系数定常条件下介质的滤波特性，但试验资料表明，不同频段的应力波在岩体的传播过程中表现出不同的频散和衰减特性［16］，采用定常黏性系数难以反映这个特性。现对黏性系数进行非定常处理，采用波形相关系数作为评价黏性系数非定常的滤波效果，假设非定常黏性系数的表达式为：

式中f，f0和η0分别为应力波频率、边界频率和定常黏性系数，q为吸收频率过渡带陡度参数。

设式（1）的解为：

式中u，u0，i和k1分别为x处的位移、振源处的位移、虚单位和复数波数。

将式（3）代入式（1），求得

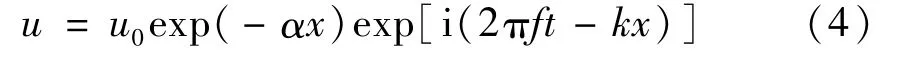
式中k为应力波实数波数，α为应力波振幅随传播距离的衰减系数，其计算公式为：

式（2）代入式（5）可求得应力波在改进Maxwell模型中传播时的衰减系数。应力波在介质中传播距离为x时的透过系数γ为：

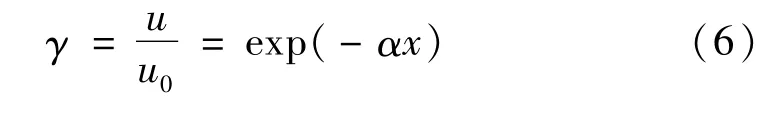
设E＝20 GPa，η0＝0．8 MPa．s，ρ＝2 500 kg·m－3，f0＝2 000 Hz，x＝1，由式（6）计算改进Maxwell模型的标准透过系数，如图1所示，图中方框为q＝15时介质的吸收频率过渡带。图1表明，陡度参数q对介质的滤波特性影响非常大，随q值增加，吸收频率过渡带陡度增加，而当q无限增大时，则所有频率低于f0的应力波均自由透过，而所有频率高于f0的应力波均完全被吸收掉；当q＝0时，改进Maxwell模型退化为标准Maxwell模型，标准Maxwell模型只能描述透过系数在频域缓变的黏弹性介质，改进Maxwell模型能够克服这个缺点。

研究表明，大部分材料并不是理想的低通滤波材料［17］，在低通频率范围表现为带通，本文假设低通范围的带通形式满足正弦变化规律。设低通频率范围［0，f0］存在n个带通，且每个带通的频带宽度相同，由式（5）和式（6）可得带通滤波函数为

式中n为频带范围内的带通数。式（7）为改进Maxwell模型的滤波函数。

图1 改进Maxwell模型的滤波特性Fig．1 Filter property of improved Maxwell model

2 试验方案

试验地点选择在德兴铜矿露天采场边坡面上，边坡角约为65°，试验点为表面平整且完整性好的岩体。如图2所示，在岩体表面，沿应力波传播方向布置5个电荷加速度传感器，传感器的参数为：电荷灵敏度10．427～14．091 PC／m·s－2；频响0．2～5 kHz；谐振频率15 kHz。用人工敲击产生振动信号，振动信号经信号调理仪进行滤波处理后再采集，信号调理仪设置为低通3 kHz，总采样率为200 kHz。按照应力波传播方向，称布设传感器的位置为测点，并编号，测点1～测点5与载荷作用点分别为0．25 m、0．55 m、1．15 m、2．35 m和4．75 m。

在试验区域进行岩石取样，进行了四组室内试验，测试得到岩石试样的物理力学参数如表1所示。通过求平均值确定试验区岩石的弹性模量为24．06 GPa，密度为2 543 kg·m－3。

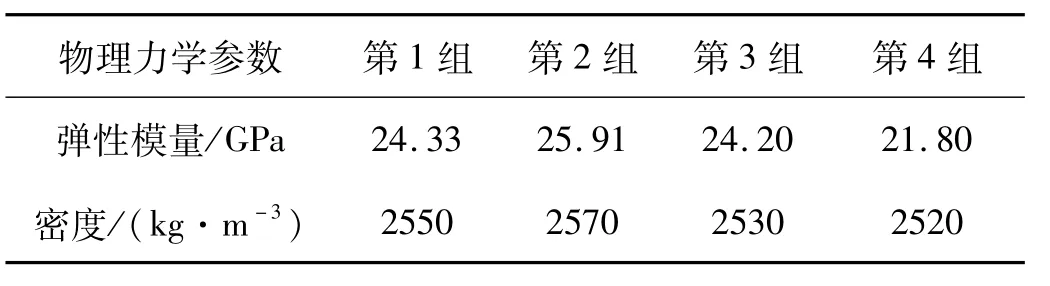
表1 岩样物理力学参数Tab.1 Physical and mechanics parameters of rock specimen

图2 试验现场Fig．2 Field testing procedure

3 完整岩体滤波特性分析

3.1 频谱分析

按照上述试验方案，采集得到完整岩体的测点振动时域波形。通过傅里叶变换得到相应波形的振幅谱，测点1、3和4的振幅谱如图3所示。从图3可以看出，测点1的应力波有三个峰值频率，分别为400 Hz、1 015 Hz和2 530 Hz，应力波从测点1传播至测点3后，高频谐波分量发生了明显的衰减，频率为2 530 Hz的应力波被完全衰减了，相对高频谐波分量而言，低频谐波分量衰减明显更弱；应力波从测点3传播至测点4后，应力波振幅谱发生明显改变，测点4的应力波只有一个峰值频率460 Hz，760 Hz以上的应力波分量全部被衰减；在应力波传播过程中发生的衰减，总体表现为低通滤波特性，同时也表现为多带通现象。由于试验区岩体的表面平整且没有肉眼能够观察到的裂纹，因此可以认为在试验区域内岩体的黏性系数没有变化，由图1可以知道，对于确定的黏性系数，标准Maxwell模型的透过系数在频域内变化比较平缓，不能解释经过短距离传播后高频谐波完全衰减的现象，因而难以采用标准Maxwell模型准确描述岩体的滤波特性，如果采用改进Maxwell模型，因引入了边界频率f0和反映介质滤波特性的参数q，黏性系数为非定常参数，因而能够描述岩体对不同频段应力波的滤波差异。

为进一步讨论应力波传播过程中参数f0和q的变化规律。对测点时域波形进行傅里叶变换得到相应的振幅谱，设测点1为振源，采用加速度振幅计算各测点透过系数γ：

式中γj为第j个测点的透过系数，aj（ω）和a1（ω）为第j测点和第一测点的加速度振幅谱。

图3 完整岩体中应力波的振幅谱Fig．3 Amplitude spectrum of stress wave propagation in intact rock mass

图4 完整岩体的滤波特性Fig．4 Filter property of intact rock mass

试验区域表面平整，可以认为应力波在半无限体中传播，设应力波为球面波，由式（8）计算得到完整岩体的滤波特性曲线，如图4所示，图4（a）为测点1传播至测点2和测点3过程中的滤波特性，图4（b）为测点1传播至测点4和测点5过程中的滤波特性。从图4可以看出，应力波透过系数在边界频率f0附件变化非常快，即吸收频率过渡带非常陡；应力波在传播过程中表现为频带非等间距的滤波特性，随频率增加，带宽有所增加。

3.2 参数拟合

由于难以直接得到冲击载荷形成的加载振幅谱，为此分析试验数据时，以第一个传感器记录的振动波形为振源信号。由于本次试验研究的应力波频率范围较小，为0～3 kHz，不考虑频散效应，由式（4）得

式中αj1为第j个测点相对于第1个测点的衰减系数，uj为第j个测点的位移。

现根据α随频率f的变化规律反分析岩体的部分力学参数。将实测数据代入式（9）计算α随频率f的变化规律，其结果代入式（5）计算力学参数。实测数据是离散数据，将式（9）写成离散形式

将图4中吸收频率过渡带的数据代入式（10），计算得到第m个测点相对于第1个测点的衰减系数随频率的dαm1／df值。

由式（2）和式（5）求得

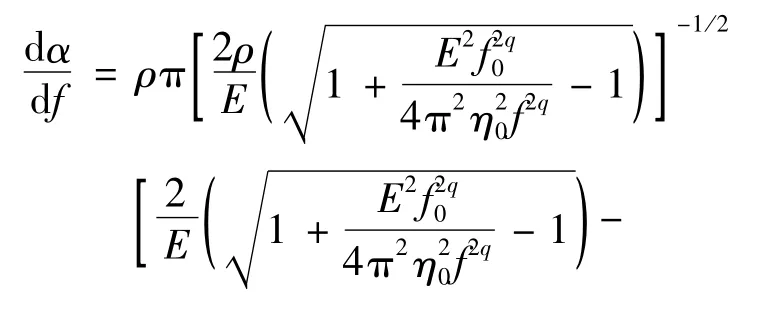
试验区域为完整岩体，假设其物理力学参数与室内岩样测试结果相同，并作为已知条件，本文通过岩样试验确定了密度、弹性模量，见表1。

采用参考文献［18］的方法确定边界频率f0，在频率吸收过渡带中找出最大透过系数，当透过系数减小至最大透过系数1／e倍时，该透过系数对应频率为边界频率f0。如测点3，由图4（a）确定吸收频率过渡带为1 920～2 500 Hz，在该频带内的最大加速度比值为0．44，由此确定边界频率为2 100 Hz。

通过前两个步骤确定了密度、弹性模量和边界频率三个参数，因而式（11）中未知参数为η0和q。试验区岩性和岩体结构没有发生变化，因而假设η0为一个未知的常数。将式（10）的计算结果代入式（11）的左边，采用最小二乘法确定η0和q。以测点3为例，图4（a）中的吸收频率过渡带1 920～2 500 Hz中有48个频率及其对应的滤波系数，测点1至测点3的距离为1．15 m，将频率、滤波系数和传播距离代入式（10），计算得到48个dαm3／df值，并代入式（11）的左边，将岩样试验确定的密度和弹性模量代入式（11）的右边，采用最小二乘法确定η0和q的值。测点3的试验数据拟合结果如图5所示，图中方框为吸收频率过渡带。所有测点拟合结果如表2所示，η0的拟合结果为0．8 MPa．s。拟合结果表明，随传播距离增加，边界频率f0快速减小，可以近似拟合成负指数关系，结果如图6所示；q值减小幅度很小，可以近似认为q值随传播距离增加不发生变化。

表2 参数拟合结果Tab.2 Parameter fitting results

图5 测点3的参数拟合Fig．5 Parameter fitting of measuring point 3

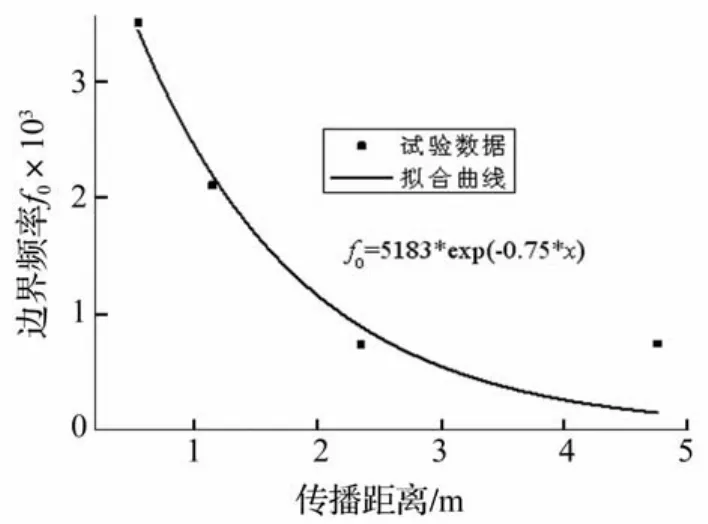
图6 传播距离与边界频率的关系Fig．6 Relationship between propagation distance and boundary frequency

3.3 带通数与滤波效果分析

为评价改进滤波函数的滤波效果，引入波形相关系数，计算公式是

式中xNi和yNi分别为实测波形和经过滤波后波形的时域离散数据，N为离散数据的总数。

对测点1的实测时域波形进行傅里叶变换得到振幅谱，采用表2的拟合结果代入式（7）进行滤波，滤波后进行傅里叶逆变换分别得到测点2～测点5的计算时域波形。采用式（12）计算，得到不同带通个数条件下的计算时域波形和实测时域波形的相关系数，结果如图7所示。从图7分析可以看出，距振源较近的区域，波形相关系数较小，说明滤波效果较差，其主要原因是采用改进Maxwell模型滤波，边界频率f0对滤波效果影响较大，进行高频滤波时，所确定的边界频率f0具有较大误差；随传播距离增加，滤波效果明显提高，如测点5的实测波形和计算波形的相关系数达到0．89，如图8所示；随着带通数增加，滤波效果先增加后减小，存在一个最优的带通数，如测点2的最优带通数为4，随传播距离增加，最优带通数减小，如测点5的最优带通数为2。

图8 测点5的实测波形和计算波形（n＝2）Fig．8 Measured waveform and calculated waveform of measuring point 5（n＝2）

图9 测点3的实测波形和计算波形（n＝1．5）Fig．9 Measured waveform and calculated waveform of measuring point 3（n＝1．5）

应力波在岩体中向前传播，受到岩体的阻尼作用，导致应力波在传播空间中发生衰减，本文提出的改进Maxwell模型描述了应力波在传播空间中发生衰减，但是测点振动的持续时间内，振动受到阻尼作用发生振幅随时间的衰减，衰减同样表现为高频谐波分量比低频谐波分量衰减快，因而测点振动波形随时间增加频率减小，而这种衰减规律不能通过空间域的滤波函数反映，因而对波形相关系数影响较大，该现象在测点3表现最为显著，如图9所示，图中带通数n＝1．5，相关系数γ＝0．57，为便于比较，图中将计算波形在时域上延迟了0．005 s。从图9中可以看出，实测波形的初始段（方框中）明显包含有高频信息，随时间增加，高频谐波被滤除，因而尾波主要是相对低频谐波分量，而采用反映随传播空间发生衰减的滤波函数，对该现象揭示的不够理想。

4 结 论

通过应力波在完整岩体中传播的现场试验发现，经过短距离传播后，应力波高频分量被完全吸收，吸收程度在频域内变化非常快，表现出突变性，而常见的黏弹性模型能够反映频域内介质对应力波吸收的缓变性。为此改进Maxwell模型，用边界频率f0作为描述控制频率吸收范围的参数，用陡度参数q描述吸收频率过渡带内应力波振幅衰减快慢程度，提出了改进Maxwell模型的滤波函数，采用相关系数描述应力波波形的变化，研究了应力波在完整岩体中滤波特性。

（1）在吸收频率过渡带内，采用最小二乘法拟合确定黏性系数非定常Maxwell模型的边界频率f0和陡度参数q，拟合结果表明：对于完整岩体，陡度参数q是常数，边界频率f0与传播距离近似成负指数关系。

（2）完整岩体总体上表现为低通滤波，在低通滤波范围内具有非等间距带通滤波特性。应力波在传播过程中频带变窄和主频降低，因而带通数减小，滤波函数存在一个最优的带通数，随传播距离增加，最优带通数逐渐减小。

（3）测点的振动波形不仅反映了应力波在传播过程中的滤波，也反映了测点振动在持时内的滤波。黏性系数非定常Maxwell模型的滤波函数只能反映应力波在传播过程中的滤波特性，振源附近含有非常丰富的高频信息，因而该模型的滤波效果较差，随传播距离增加，滤波效果明显提高，当传播距离为4．75 m时，波形相关系数达到0．89，表明黏性系数非定常Maxwell模型能够有效描述完整岩体的滤波特性。选择合适的带通数，即使距测点1（本文假设为振源信号）距离为0．3 m的测点2，波形相关系数也达到0．69，表明岩体的滤波主要发生在传播路径，振动持时内的滤波是次要的。

［1］Müller T M，Gurevich B，Lebedev M．Seismic wave attenuation anddispersionresultingformwave-inducedflowin porousrocks：a review［J］．Geophysics，2010，75（5）：75A147－75A164．

［2］Wang Z，Nur A．Dispersion analysis of acoustic velocities in rocks［J］．Journal of the Acoustical Society of America，1990，87（6）：2384－2395．

［3］王海洋，孙赞东，Mark Chapman．岩石中波传播速度频散与衰减［J］．石油学报，2012，33（2）：332－342．

WANG Hai-yang，SUN Zan-dong，Mark Chapman．Velocity dispersion and attenuation of seismic wave propagation in rocks［J］．ACTA Petrolei Sinica，2012，33（2）：332－342．

［4］孙成禹，印兴耀．三参数常Q粘弹性模型构造方法研究［J］．地震学报，2007，29（4）：348－357．

SUN Cheng-yu，YINXing-yao．Constructionofconstant qviscoelastic modelwiththreeparameters［J］．ACTA Seismologica Sinica，2007，29（4）：348－357．

［5］Maranini E，Brignoli M．Creep behavior of a weakrock：experimental characterization［J］．JournalofStructural Geology，2005，27（6）：948－963．

［6］Fabre G，Pellet F．Creep and time-dependent damage in argillaceous rocks［J］．InternationalJournalofRock Mechanics and Mining Sciences，2006，43（6）：950－960．

［7］徐卫亚，杨圣奇，褚卫江．岩石非线性黏弹塑性流变模型（河海模型）及其应用［J］．岩石力学与工程学报，2006，25 （3）：433－447．

XU Wei-ya，YANG Sheng-qi，CHU Wei-jiang．Nonlinear viscoelasto plastic rheological model（hohai model）of rock and its engineering application［J］．Chinese Journal of Rock Mechanics and Engineering，2006，25（3）：433－447．

［8］熊良宵，杨林德，张尧．岩石的非定常Burgers模型［J］．中南大学学报（自然科学版），2010，41（2）：679－684．

XIONG Liang-xiao，YANGLin-de，ZHANGYao．Nonstationary Burgers model for rock［J］．Journal of Central South University（Science and Technology），2010，41（2）：679 －684．

［9］刘林超，张卫．具有分数Kelvin模型的粘弹性岩体中水平圆形硐室的变形特性［J］．岩土力学，2005，26（2）：287－289．

LIU Lin-chao，ZHANGWei．Deformationpropertiesof horizontal round adits in viscoelastic rocks with fractional Kelvin model［J］．Rock and Soil Mechanics，2005，26（2）：287－289．

［10］施行觉，李成波，Adnan Aydin等．地球介质的非定常参数黏弹模型［J］．地球物理学报，2009，52（1）：50－56．

SHI Xing-jue，LI Cheng-bo，Adnan Aydin，et al．Viscoe-lastic model with variable parameters for earth medium［J］．Chinese J Geophs，2009，52（1）：50－56．

［11］张波，李术才，张敦福等．简谐波在黏弹性介质中波动传播的应力场研究［J］．岩土力学，2011，32（8）：2449－2454．

ZHANG Bo，LI Shu-cai，ZHANG Dun-fu，et a1．Study of stressfieldsofsimpleharmonicwavepropagationin viscoelastic media［J］．Rock and Soil Echanics，2011，32 （8）：2449－2454．

［12］黄小华，冯夏庭，陈炳瑞．广义黏弹组合模型的等效性及其基本性质［J］．力学学报，2010，42（1）：65－73．

HUANGXiao-hua，FENGXia-ting，CHENBing-rui．Equivalences of the generalized viscoelastic models and their inherent properties［J］．Chinese Journal of Theoretieal and Applied Mechanies，2010，42（1）：65－73．

［13］吴庆曾，李洪涛，杨进平．声波检测穿透信号波形变化规律和量化的探讨［J］．物探与化探，2012，36（1）：144－148．

WU Qing-zeng，LI Hong-tao，YANG Jin-ping．Discussion on the variation and quantification of penetrating signal waveform in acoustic wave detection［J］．Seophysical＆Geochemical Exploration，2012，36（1）：144－148．［14］樊耀新．断层对地震子波波形影响的研究［J］．西北地震学报，1996，18（3）：54－59．

FAN Yao-xin．Study about influence of fault on seismic wavelet form［J］．Northwestern Seismological Journal，1996，18（3）：54－59．

［15］王礼立．应力波基础［M］．北京：国防工业出版社，2005．

［16］凌同华，张胜，易志强等．岩石声发射信号能量分布特征的EMD分析［J］．振动与冲击，2012，31（11）：26－31．

LING Tong-hua，ZHANG Sheng，YI Zhi-qiang，et al．Energy distribution characteristics of rock acoustic emission signals with EMD analysis［J］．Journal of Vibration and Shock，2012，31（11）：26－31．

［17］张天骐，谭方青，高春霞，等．一种新的窗函数法设计余弦调制滤波器组系统［J］．系统工程与电子技术，2011，33 （12）：2737－2742．

ZHANG Tian-qi，TAN Fang-qing，GAO Chun-xia，et al．New windowing approach for designing cosine-modulated filter bank systems［J］．Systems Engineering and Electronics，2011，33（12）：2737－2742．

［18］Ricker N H．黏弹性介质中的地震波［M］．北京：地质出版社，1981．

Filtering property of intact rock mass to stress wave within scope of log frequency

WANG Guan-shi1，HU Shi-li1，2，LI Zhi-wen1，WANG Xing-guang1
（1．Jiangxi University of Science and Technology，Ganzhou 341000，China；2．China University of Geosciences，Beijing 100083，China）

The effects of stress wave in different frequency ranges on attenuation coefficient are different．The filtering properties of stress wave propagating in intact rock mass within scope of log frequency were studied through field test．Based on the shortcoming of common viscoelastic model predicting the relationship between attenuation coefficient and frequency，Maxwell model for unsteady viscosity coefficient was established after the unsteady treatment of viscosity coefficient．The filtering effect of the improved model was evaluated using the waveform correlation coefficient．The study results indicated that intact rock mass has a low-pass filtering property and unequal interval band-pass property within scope of a low-pass filter，the number of band-pass decreases with increase in propagation distance；attenuation coefficients of stress wave with frequency change greatly in the transition zone of absorption frequency，the change rule of attenuation coefficient of stress wave propagation in intact rock mass is effectively described with the improved Maxwell model for unsteady viscosity coefficient；the boundary frequency of the transition zone of absorption frequency has a negative exponential relationship with propagation distance，the edge gradient parameter of the transition zone of absorption frequency is approximately constant．The filtering effect of intact rock mass improves obviously using the improved Maxwell model with increase in propagation distance；the waveform correlation coefficient reaches 0．89 when propagation distance of stress wave is 4．75m；the improved model is capable of describing the filtering properties of intact rock mass．

intact rock mass；filter property；Maxwell model；stress wave；attenuation coefficient

TU452

A

10．13465／j．cnki．jvs．2014．23．023

国家自然科学基金资助项目（51104069）；江西省自然科学基金项目（2010GQC0067）；江西省教育厅科技项目（GJJ12339，GJJ11130）

2014－01－27 修改稿收到日期：2014－03－19

王观石男，博士，副教授，1977年生