考虑稳定匹配条件的双边满意匹配决策方法
2014-05-16樊治平李铭洋
樊治平,李铭洋,2,乐 琦
(1.东北大学工商管理学院,辽宁沈阳110819;2.沈阳化工大学数理系,辽宁沈阳110142;3.江西财经大学信息管理学院,江西南昌330013)
考虑稳定匹配条件的双边满意匹配决策方法
樊治平1,李铭洋1,2,乐 琦3
(1.东北大学工商管理学院,辽宁沈阳110819;2.沈阳化工大学数理系,辽宁沈阳110142;3.江西财经大学信息管理学院,江西南昌330013)
双边匹配问题是指如何在两个不相交的主体集合中依据各主体针对潜在匹配对象给出的偏好信息来确定合适的匹配结果,其在经济管理领域中存在着大量的实际背景,是许多学者关注的研究课题。在本文中,针对双边主体给出偏好序值信息的双边匹配问题,给出了一种考虑稳定匹配条件的双边满意匹配决策方法。首先给出了双边匹配、稳定匹配和满意匹配的相关概念;然后考虑到稳定匹配条件,并以双边主体满意度最大为目标,构建了多目标双边匹配优化模型;进一步地,采用线性加权法将多目标优化模型转换为单目标优化模型,并通过求解优化模型来获得最优匹配结果。最后,通过一个算例说明了本文提出方法的实用性和有效性。
双边匹配;序值;稳定匹配;满意度;满意匹配;优化模型
1 引言
最早的双边匹配问题研究是Gale和Shapley[1]针对男女婚姻匹配问题进行了研究。之后,有关双边匹配问题的研究得到了许多学者的关注[2-14]。特别是近年来,可以看到一些具有实际背景的双边匹配问题研究,如电子商务环境下的供需双边匹配[2-3]、人力资源管理中员工与岗位的匹配[4-5]、广告代理商与广告客户的匹配[6]、风险投资商与风险企业的匹配[7]等。在双边匹配问题研究中,关于双边给出偏好序值(或序)信息的双边匹配方法研究,一直是学者们多年来关注的研究重点[8-16]。针对这方面的研究,Gale和Shapley[1]最早提出了男女婚姻稳定匹配的概念,并给出了获得男方或女方最优稳定匹配结果的求解算法;Roth[8]针对婚姻匹配问题研究给出了具有一般意义的双边匹配概念;Mc Vitie和Wilson[9-10]给出了一种基于“Breakmarriage Operation”的递归算法来获得婚姻匹配的全部稳定匹配解,同时又研究了男女双方人数不相等情形的婚姻匹配问题,并给出了有针对性的稳定匹配概念和求解算法;Halldórsson等[11]针对具有不完全或无差异偏好序值信息的稳定婚姻问题研究,给出一个随机逼近算法;Vate和John[12]以及Roth等[13]通过构建并求解考虑稳定匹配约束条件的线性规划模型来得到男方或女方最优稳定匹配结果;还有一些学者着重研究了考虑不完全或无差异偏好序值信息的双边稳定匹配算法的复杂性[14-16]。需要指出的是,已有的研究成果大多是基于稳定匹配的视角,求出一方或双方偏好序值之和最小的稳定匹配结果[9-13],而这种做法的实质是假设主体对于匹配结果的满意程度与偏好序值呈逆线性关系,这在一些现实匹配问题中显得不尽合理。例如在婚姻匹配问题中,某男士对8位女士进行排序,该男士对排名第1与排名第2的两位女士之间满意程度的差距,通常要比排名第7和排名第8的两位女士之间的差距要大。因此,如何刻画在双边匹配中双方主体的满意度,进而获得“既稳定、又满意”的匹配结果是一个值得深入研究的问题。鉴于此,本文针对双边主体给出偏好序值信息的双边匹配问题,给出一种考虑稳定匹配条件的满意双边匹配决策方法。给出的方法是基于与已有方法不同的研究视角,即基于满意匹配的研究视角来解决双边匹配问题,通过对双边匹配中双方主体满意度的刻画,构建考虑稳定匹配约束条件的双边满意匹配优化模型,求得同时兼顾了“稳定”和“满意”两种要求的双边匹配结果。
2 双边匹配的相关概念
2.1 双边匹配
记I={1,2,…,m},J={1,2,…,n},且不妨设m≤n。设甲方主体集合为A={A1,A2,…,Am},其中Ai表示第i个甲方主体,i∈I;乙方主体集合为B={B1,B2,…,Bn},其中Bj表示第j个乙方主体,j∈J。依据文献[17-19],下面给出关于双边匹配的定义。
定义1 一一映射μ:A∪B→A∪B称为双边匹配,当且仅当∀Ai∈A、∀Bj∈B满足下列条件:(1)μ(Ai)∈B;(2)μ(Bj)∈A∪Bj;(3)若μ(Ai)=Bj,则μ(Bj)=Ai。
定义1中,μ(Ai)=Bj表示Ai与Bj在μ中匹配,此时称(Ai,Bj)为μ-匹配主体对。由定义1中的条件(3)可知,若(Ai,Bj)为μ-匹配主体对,则(Bj,Ai)也为μ-匹配主体对。μ(Bj)=Bj表示Bj在μ中未匹配,此时记(Bj,Bj)为μ-匹配主体对。因此,双边匹配μ可表示为μ=μt∪μs,其中,μt={(Ai,Bf(i))|i=1,…,m},μs={(Bj,Bj)| j={1,…,n}{f(1),…,f(m)}},f(i)∈J,且∀k,l∈I,k≠l,有f(k)≠f(l)。
根据以上描述,双边匹配问题如图1所示。在双边匹配μ中,由于m≤n,因此,针对甲方主体集合A中的每一个主体Ai,乙方主体集合中都存在不同的主体Bj与之构成一个μ-匹配主体对,且乙方主体集合中有n-m个主体未匹配。
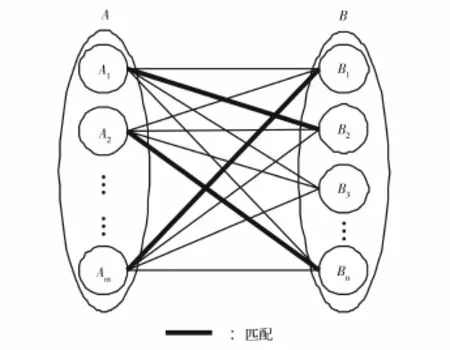
图1 双边匹配问题示意图
对于主体A1,可在B中全部的n个主体中选择一个与其构成匹配主体对;在A1确定好匹配对象之后,对于主体A2,可在B中剩余的n-1个主体中选择一个与其构成匹配主体对;以此类推,对于主体Am,在其余的m-1个甲方主体确定好匹配对象之后,可在B中剩余的n-m+1个主体中选择一个与其构成匹配主体对。因此,对于考虑的双边匹配问题,共有n(n-1)…(n-m+1)种可能的双边匹配。为分析方便,记γ=n(n-1)…(n-m+1),所有双边匹配构成的集合记为HT={μ1,μ2,…,μγ},其中μk表示第k个双边匹配(k∈{1,2,…,γ})。双边匹配决策就是依据某种准则在双边匹配集合HT中找到合适的双边匹配μ,以尽量满足双方主体的需求或要求。
2.2 稳定匹配
在考虑的双边匹配问题中,假设甲方主体Ai(i∈I)和乙方主体Bj(j∈J)给出的偏好信息均为序值。记R=[rij]m×n为甲方针对乙方给出偏好信息的序值矩阵,其中rij表示甲方主体Ai把乙方主体Bj排在第rij位,rij∈J;T=[tij]m×n为乙方针对甲方给出偏好信息的序值矩阵,其中tij表示乙方主体Bj把甲方主体Ai排在第tij位,tij∈I。下面给出关于稳定匹配的定义[1,17-19]。
定义2 对于双边匹配μ,若以下两种情况均未出现:
(1)∃Ai,Al∈A,Bj,Bk∈B,μ(Ai)=Bk,μ(Al)=Bj,满足rij<rik且tij<tlj;
(2)∃Ai,Al∈A,Bj∈B,μ(Ai)=Bk,μ(Bj)=Bj,满足rij<rik,
则称μ为稳定匹配,即μ为具有稳定性的匹配,否则称μ为不稳定匹配。
可以看出,满足定义2中情况(1)或(2)的主体对(Ai,Bj),会使双边匹配μ不稳定,这是因为主体Ai与Bj相互间都认为对方要优于目前所匹配的主体,此时称主体对 (Ai,Bj)为μ-阻碍稳定对[1,17-19]。
为了理解稳定匹配的实际含义,下面举例说明。
例1 在婚姻匹配问题中,设男士集合为A={A1,A2,A3},女士集合为B={B1,B2,B3,B4},男方针对女方给出偏好信息的序值矩阵为R,女方针对男方给出偏好信息的序值矩阵为T,R和T分别为

进一步地,给出如下3个双边匹配:

那么,依据定义2可知:双边匹配μ1是不稳定匹配,这是因为对于μ1,主体对(A3,B3)为μ-阻碍稳定对,在A3给出的序值中,r33<r34,即A3认为B3要优于目前所匹配的主体B4,而B4又未匹配,符合定义2中的情况(2);双边匹配μ2和μ3均为稳定匹配,这是因为对于μ2和μ3都不存在μ-阻碍稳定对。
基于上述分析可知,对于一个现实的双边匹配问题,一般会同时存在多个稳定匹配,如何刻画这些双边匹配的“优劣”是一个需要关注的问题。为此,下面给出关于满意匹配的相关概念。
2.3 满意匹配
双方主体给出的偏好序值信息在一定程度上反映了双方主体间的相互满意程度,但在现实中,偏好序值的增加(减小)与满意程度的降低(增加)之间不一定呈线性关系。这里,为了更好地刻画一方主体对另一方主体的满意程度,给出关于满意度的定义如下:
定义3 设κij为甲方主体Ai对乙方主体Bj的满意度,βij为乙方主体Bj对甲方主体Ai的满意度,则满意度κij与βij可分别表示为:
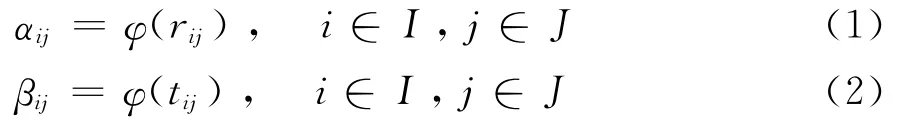
其中,φ(·)为严格单调递减函数,满足φ(·)>0,φ(1)=1。
注1 在定义3中,函数φ(·)可以是多种表示形式,若考虑主体的心理感受或心理因素,则φ(·)还应满足φ″(·)>0。本文考虑给出如下形式:

依据式(1)-(3),可将偏好序值rij与tij转化为满意度κij与βij(i∈I;j∈J),进而构建甲方主体满意度矩阵=[κij]m×n与乙方主体满意度矩阵=[βij]m×n。
定义4 设μ=μt∪μs为甲方主体集合A与乙方主体集合B之间的双边匹配,其中μt={(Ai,Bf(i))|i∈I,f(i)∈J},μs={(Bj,Bj)|j={1,…,n}{f(1),…,f(m)}},则称:
(1)甲方主体A1,A2,…,Am的满意度之和为双边匹配μ的甲方总体满意度,记为φ~(μ),即:

(2)乙方主体Bf(1),Bf(2),…,Bf(m)的满意度之和为双边匹配μ的乙方总体满意度,记为φ~~(μ),即:

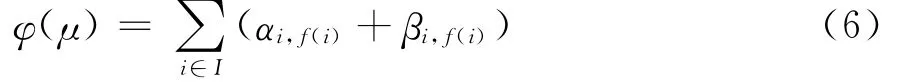
定义5 设H={μ1,μ2…,μg}为甲方主体集合A与乙方主体集合B之间的任一双边匹配集合,若则称匹配μA为H中的甲方满意匹配;若},μB∈H,则称匹配μB为 H中的乙方满意匹配;若φ(μ*)= max{φ(μ1),φ(μ2),…,φ(μg)},μ*∈H,则称匹配μ*为H中的双方满意匹配。
(3)双方主体的满意度之和为双边匹配μ的双方总体满意度,记为φ(μ),即:
3 双边匹配决策方法
3.1 优化模型建立
在考虑的基于偏好序值信息的双边匹配问题中,获得稳定匹配结果是有其现实意义的[20-22],这是因为:若匹配结果是不稳定的,则存在两个未匹配的主体,他们相互之间的偏好程度均优于目前所匹配的主体,换句话说,他们有着放弃目前所匹配的主体而相互匹配在一起的“动机”。因此,结合实际双边匹配问题的要求,在稳定匹配集合中依据满意度最大化的原则寻求相应的匹配结果是比较合理的。这样,本文要解决的问题就是:依据甲乙双方给出的偏好序值矩阵R和T,通过某种决策方法,在稳定匹配集合中依据一定准则获得尽可能使双方主体满意程度高的匹配结果。
为了求解上述问题,引入0-1变量xij,其中:

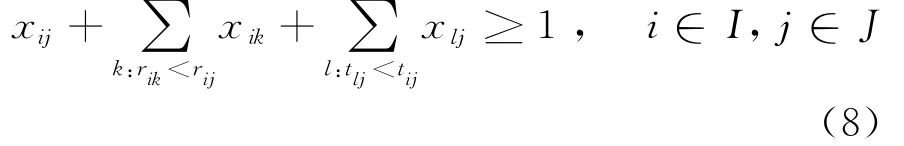
易见,对于甲乙双方主体数目分别为m与n的双边匹配问题,稳定匹配约束条件共有mn个。这里,仍以例1为例进行阐释,由于m=3和n=4,故稳定匹配约束条件有12个,即:
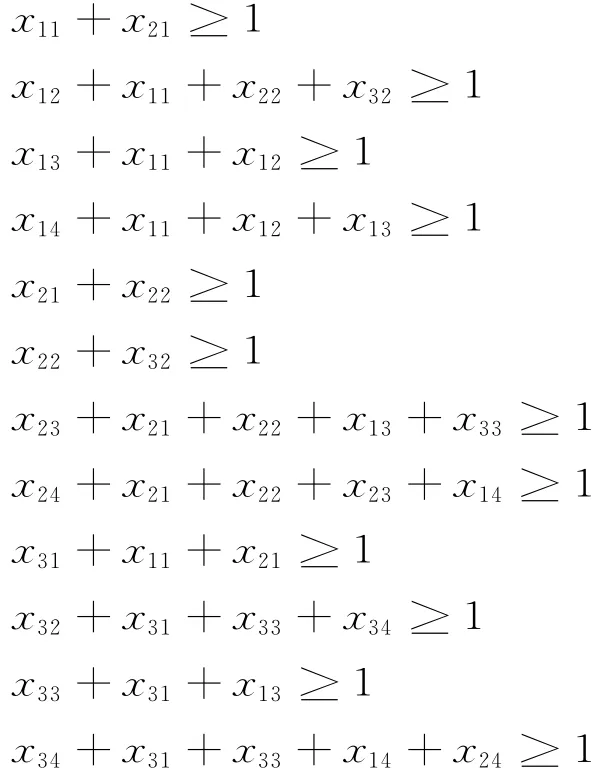
为了更好地说明稳定匹配约束条件的确定方法,这里以上述稳定匹配约束条件中第1个约束条件“x11+x21≥1”为例进行说明:考虑到r11=1,可知不存在r1k(k=2,3,4),使得r1k<r11,又因为1=t21<t11=2,因此,根据式(8)可知,主体对(A1,B1)的稳定性约束条件为x11+x21≥1;其余的11个稳定匹配约束条件亦可通过同样的方法获得。
进一步地,在考虑稳定匹配条件的情况下,以甲、乙各方总体满意度最大为目标,可建立如下多目标优化模型:

依据式(7),可构建一个匹配矩阵X=[xij]m×n。
根据定义2可知,在稳定匹配μ中,若μ(Ai)≠Bj,则以下两个条件至少满足其一:
(1)μ(Ai)=Bk,其中Bk∈B,rik<rij
(2)μ(Al)=Bj,其中Al∈A,tlj<tij
否则(Ai,Bj)就构成一个μ-阻碍稳定对。
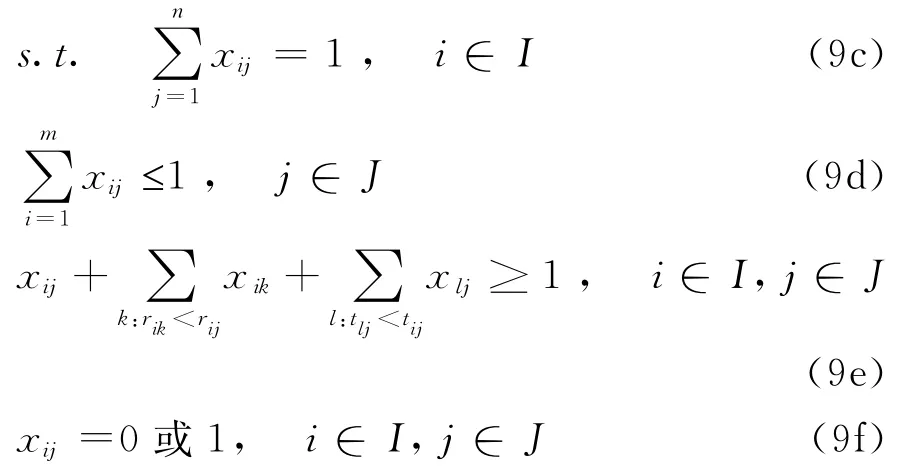
考虑稳定匹配的约束条件可表示为[12-13]:在模型(9)中,式(9a)和式(9b)为目标函数,其含义分别是尽可能使双边匹配μ的甲方总体满意度和乙方总体满意度最大。式(9c)和式(9d)为双边匹配的约束条件,由于m≤n,故式(9c)为等式约束,其含义是每个甲方主体都必须与一个乙方主体匹配;式(9d)为不等式约束,其含义是每个乙方主体最多与一个甲方主体匹配;换句话说,在匹配矩阵X中,每行中有一个元素为1,其余元素为0;每列中最多有一个元素为1,其余元素为0。式(9e)为稳定匹配约束条件,其确保了通过求解模型(9)获得的匹配结果为稳定匹配。
3.2 模型求解
为求解上述多目标优化模型(9),采用线性加权法[23],将式(9a)和式(9b)进行加权。设w1和w2分别表示目标Z1和Z2的权重或重要程度,满足0≤w1,w2≤1,w1+w2=1,则模型(9)可转化为如下单目标优化模型:
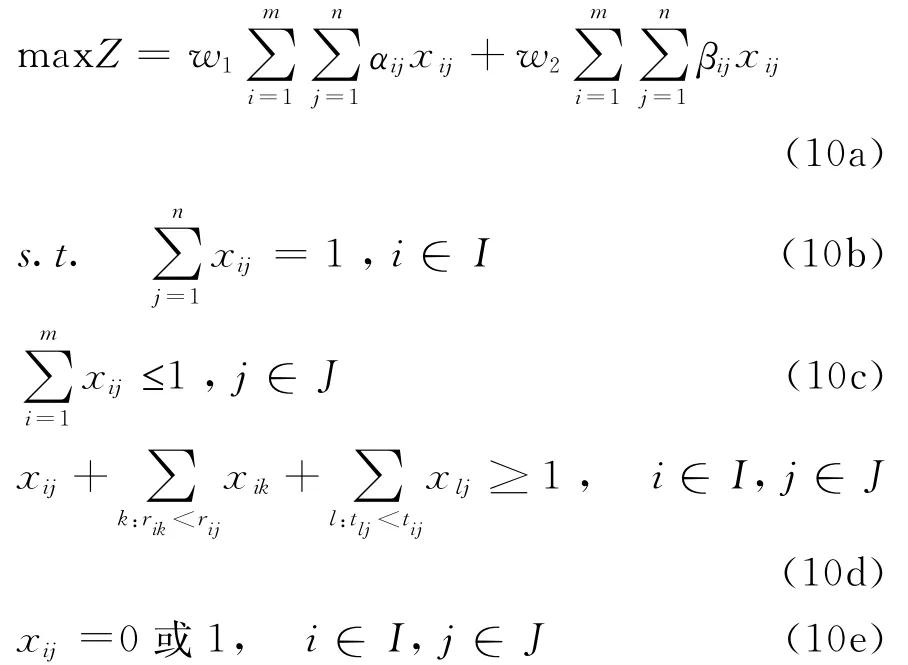
对于模型(10),有如下结论。
定理1 模型(10)存在最优解。
证明:由于模型(10)为含有mn个变量的0-1规划模型,故其最多具有2mn个可行解,即模型(10)的可行解为有限多个。依据Gale等[1]可知,本文考虑的双边匹配问题必存在稳定匹配解,故由式(10b)-(10e)构成的可行域非空,即模型(10)至少存在一个可行解。因此,模型(10)必存在最优解。
模型(10)中目标函数和约束条件均是线性的,因此可采用整数规划方法进行求解[24]。考虑到现实中基于偏好序值信息的双边匹配问题规模一般不是很大,即双边主体的数目一般不是很多,所以针对变量数目不是很多情形的模型(10),可以使用专门的优化软件包进行求解,如可以使用LINGO11.0、Cplex9.0等优化软件包求解模型(10)。若双边匹配问题的规模较大,可进行优化模型的复杂性分析,进而尝试设计启发式方法或遗传算法等求解模型(10)。
综上,求解基于偏好序值信息的双边匹配问题的计算步骤如下:
步骤1 依据式(1)和(3),将序值rij转化为满意度κij,并构建甲方主体满意度矩阵=[κij]m×n;
步骤2 依据式(2)和(3),将序值tij转化为满意度βij,并构建乙方主体满意度矩阵=[βij]m×n;
步骤4 使用线性加权法将优化模型(9)转化为优化模型(10);
步骤5 求解优化模型(10),获得匹配结果。
4 算例分析
考虑一个现实中的求职者与岗位的双边匹配问题。MC公司是一家期货经纪公司,主要从事期货交易咨询、代理买卖期货合约等业务。该公司在最新的一批人员招聘中,拟针对5个空缺的管理岗位(A1,A2,…,A5)进行招聘。现有多名求职者前来应聘,经过初筛之后,有7名求职者(B1,B2,…,B7)符合该公司的各项基本要求,从而进入了最终的面试考核环节。在对7名求职者进行面试之后,该公司的人力资源部门从性格、管理经验、专业能力、沟通能力以及团队合作能力等5个指标对各个求职者进行评价,给出各岗位针对不同求职者的偏好序值rij,i=1,2,…,5,j=1,2,…,7。各求职者从薪水和福利、发展前景、劳动强度以及工作环境等4个指标对不同岗位进行评价,给出各求职者针对不同岗位的偏好序值tij,i=1,2,…,5,j=1,2,…,7。记R=[rij]5×7表示岗位针对求职者的偏好序值矩阵,T=[tij]5×7表示求职者针对岗位的偏好序值矩阵,假设R和T分别为:

为了获得求职者与岗位的双边匹配结果,下面简要说明采用前文给出方法的部分计算过程及结果。
依据偏好序值矩阵R和T,运用式(1)-(3),计算满意度κij和βij(i=1,…,5;j=1,…,7),并构建满意度矩阵=[κij]5×7与=[βij]5×7如下:

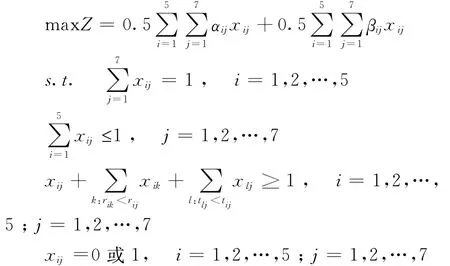
使用LINGO11.0软件包求解上述模型,可得匹配矩阵为:
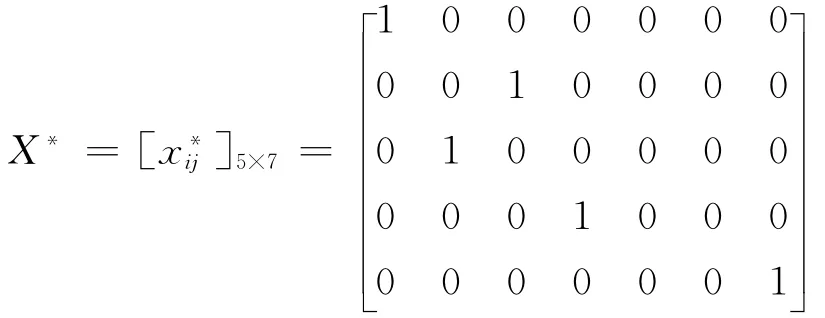
此时目标值为Z*=3.14,得到的最优匹配结果为:
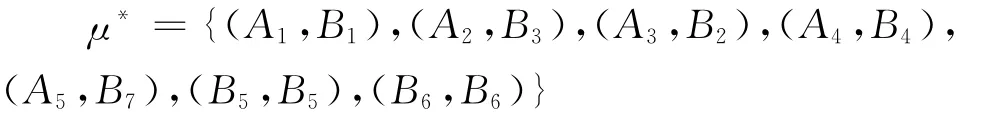
即A1与B1匹配、A2与B3匹配、A3与B2匹配、A4与B4匹配、A5与B7匹配、B5和B6未匹配。
为进一步说明稳定匹配的意义,给出如下分析。
在本例中,若不考虑双边匹配稳定性,即在上述模型中不考虑稳定匹配约束条件,那么通过模型求解可得匹配矩阵为:
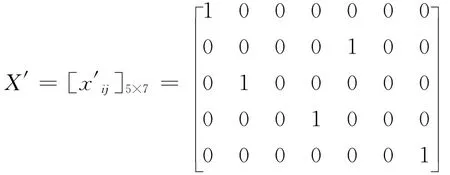
此时目标值为Z′=3.35,得到的匹配结果为
μ′={(A1,B1),(A2,B5),(A3,B2),(A4,B4),(A5,B7),(B3,B3),(B6,B6)}
即A1与B1匹配、A2与B5匹配、A3与B2匹配、A4与B4匹配、A5与B7匹配、B3和B6未匹配。
将上述两个匹配结果进行对比分析,可以看到,虽然匹配μ′比匹配μ*的双方总体满意度高,但μ′却是不稳定匹配,主体对(A2,B3)为μ-阻碍稳定对,这是因为r23=3<4=r25,即该公司认为求职者B3相比B5来说更适合岗位A2,而B3却未匹配。换句话说,在信息透明的情况下,若按照μ′来确定岗位录用结果,B3会因为自己比B5更适合岗位A2却未被录用而不满,公司也会因岗位A2未录用比B5更好的员工B3而产生不满。因此,选择匹配μ*作为最优匹配结果,具有较好的现实意义。
5 结语
本文给出了一种考虑稳定匹配条件的满意双边匹配决策方法,该方法是针对双边主体给出的偏好序值信息,通过构建满意度函数来计算匹配满意度,并在考虑稳定匹配条件的前提下,以双边主体满意度最大为目标,构建了多目标双边匹配优化模型,通过求解优化模型可获得最优匹配结果。与已有的方法相比,本文提出的方法可以求得在稳定匹配集合中使双方主体各自总体满意度尽可能大的匹配结果,这样的匹配结果在一定程度上兼顾了“稳定”和“满意”两种要求。本文提出的方法具有较好的理论支撑,具有概念清晰、易操作等特点,也具有实际应用价值,为解决基于偏好序值信息的双边匹配问题提供了一种新的途径。
[1]Gale D,Shapley L.College admissions and the stability of marriage[J].American Mathematical Monthly,1962,69(1):9-15.
[2]Janssen M,Verbraeck A.Comparing the strengths and weaknesses of Internet-based matching mechanisms for the transport market[J].Transportation Research Part E,2008,44(3):475-490.
[3]Sarne D,Kraus S.Managing parallel inquiries in agents'two-sided search[J].Artificial Intelligence,2008,172(4-5):541-569.
[4]Lin H T.A job placement intervention using fuzzy approach for two-way choice[J].Expert Systems with Applications,2009,36(2):2543-2553.
[5]Huang D K,Chiu H N,Yeh R H,et al.A fuzzy multicriteria decision making approach for solving a bi-objective personnel assignment problem[J].Computers& Industrial Engineering,2009,56(1):1-10.
[6]Kaiser U,Wright J.Price structure in two-sided markets:Evidence from the magazine industry[J].International Journal of Industrial Organization,2006,24(1):1-28.
[7]Elitzur R,Gavious A.A multi-period game theoretic model of venture capitalists and entrepreneurs[J].European Journal of Operational Research,2003,144(2):440-453.
[8]Roth A E.Common and conflicting interests in two-sided matching markets[J].European Economic Review,1985,27(1):75-96.
[9]Mc Vitie D G,Wilson L B.The stable marriage problem[J].Communications of the Association for Computing Machinery,1971,14(7):486-492.
[10]Mcvitie D G,Wilson L B.Stable marriage assignment for unequal sets[J].Bit Numerical mathematics,1970,10(3):295-309.
[11]Halldórsson M M,Iwama K,Miyazaki S,et al.Randomized approximation of the stable marriage problem[J].Theoretical Computer Science,2004,325(3),439-465.
[12]Vate V,John H.Linear programming brings marital bliss[J].Operations Research Letters,1989,8(3):1 -23.
[13]Roth A E,Rothblum U G,John H,et al.Stable matchings,optimal assignments and linear programming[J].Mathematics of Operations Research,1993,18(4):803-828.
[14]Iwama K,Manlove D,Miyazaki S,et al.Stable marriage with incomplete lists and ties[C]//Giorgio A,Mariangiola D C,Simonetha R.Proceedings ICALP' 99:The 26th International Colloquium on Automata,Languages,and Programming,Lecture Notes in Computer Science,Springer,Berlin,1999,1644:443-452.
[15]Manlove D F,Irving R W,Iwama K,et al.Hard variants of stable marriage[J].Theoretical Computer Science,2002,276(1-2):261-279.
[16]Iwama K,Miyazaki S,Yamauchi N.A(2-c/)-approximation algorithm for the stable marriage problem[J].Algorithmica,2008,51(3):342-356.
[17]Teo C P,Sethuraman J,Tan W P.Gale-Shapley stable marriage problem revisited strategic issues and applications[J].Management Science,2001,47(9):1252-1267.
[18]Gale D.The two-sided matching problem:Origin,development and current issues[J].International Game Theory Review,2001,3(2-3):237-252.
[19]Echenique F.What matchings can be stable?The testable implications of matching theory[J].Mathematics of Operations Research,2008,33(3):757-768.
[20]党兴华,贾卫峰.GS匹配算法在企业技术创新网络结构形成中的应用[J].系统工程,2009,27(4):31-36.
[21]Clark S,Kanbur R.Stable partnerships,matching,and local public goods[J].European Economic Review,2004,48(4):905-925.
[22]Alkan A,Gale D.Stable schedule matching under revealed preference[J].Journal of Economic Theory,2003,112(2):289-306.
[23]Cohon J L.Multiobjective programming and planning[M]//Mustoe L R,Barry M D J.Mathematics in Science and Engineering,New York:Academic Press,1978.
[24]钱颂迪.运筹学[M].北京:清华大学出版社,1996.
Decision Analysis Method for Two-Sided Satisfied Matching Considering Stable Matching Condition
FAN Zhi-ping1,LI Ming-yang1,2,YUE Qi3
(1.School of Business Administration,Northeastern University,Shenyang 110819,China;2.Department of Science,Shenyang University of Chemical Technology,Shenyang 110142,China;3.School of Information Management,Jiangxi University of Finance and Economics,Nanchang 330013,China)
Two-sided matching problem refers to how to obtain proper matching result from two disjoint sets of agents according to the preference information of each agent for potential partners from the opposite set.It is a research topic with extensive practical backgrounds in the field of economic management and attracts the attention of many scholars.In this paper,a decision analysis method for two-sided satisfied matching considering stable matching condition is proposed to solve the two-sided matching problem,in which the preference ordinal numbers are provided by agents on both sides.Firstly,the related concepts on two-sided matching,stable matching and satisfied matching are given.Then,considering the stable matching condition,a multi-objective two-sided matching optimization model which maximizes the satisfaction degrees of two-sided agents is constructed.Furthermore,the linear weighted method is used to convert the multi-objective optimization model into a single-objective optimization model,and the optimal matching result can be obtained by solving the model.Finally,a numerical example is given to illustrate the practicality and effectiveness of the method proposed in this paper.
two-sided matching;ordinal number;stable matching;satisfaction degree;satisfied matching;optimization model
C 934
:A
1003-207(2014)04-0112-07
2012-02-15;
2013-01-22
国家自然科学基金资助项目(71271051,71371002);辽宁省高等学校创新团队支持计划项目(WT2013004);中央高校基本科研业务费专项资金资助项目(N110706001)
樊治平(1961-),男(汉族),江苏镇江人,东北大学工商管理学院教授,博士生导师,研究方向:运作管理与决策分析.
