RBF神经网络在旋转机械故障诊断中的应用

陈 松

（安徽建筑大学 机械与电气工程学院，合肥 230601）

旋转机械故障的诊断可以通过测量振动信号、振声、温度、油液或光谱来实现.对于振动信号有时域特征提取、时序特征提取、频谱特征提取、时频特征提取、高阶谱特征提取和小波频带特征提取等方法.对于各种特征量的识别，应用较多的算法有：模糊集合、专家系统、神经网络等［1-3］.故障特征与故障模式并不是简单的一一对应关系，其构成的故障特征空间比较复杂，常常不是线性可分的，而神经网络能够映射任意复杂的非线性关系，具有自学习、自组织、自适应等特性，并且有极强的容错和联想能力、较快的计算速度，所以神经网络被广泛用于机械故障诊断识别中.

目前广泛应用的是BP神经网络，它能反映诊断过程的本质，静态模式识别能力强，可实现任意复杂的判决表面，具有自学习及自适应能力［4］.但BP网络采用的是梯度下降的搜索算法，这就不可避免地出现了网络收敛速度慢、容易陷入局部极小、学习结果受初始权值分布影响较大、结果不稳定等问题.Elman神经网络作为一种重要的动态反馈性学习模型，通过增加结构单元对各个样本的相互关联进行记忆，实现动态建模，该模型具有极强的复杂模式动态映射能力，更是一种极具潜力的复杂故障模式辨识工具.但由于Elman神经网路的学习过程与前馈神经网络类似，难免会出现收敛速度慢和易收敛到局部极小的缺陷，导致故障模式辨识结果不稳定［5］.

径向基函数神经网络（Radical Basis Function神经网络）是一种高效的前馈式神经网络，它具有其他前向网络所不具有的最佳逼近性能和全局最优特性，可以避免陷入局部极小的可能，并且结构简单，训练速度快.它也是一种可以广泛应用于模式识别、非线性函数逼近等领域的神经网络模型.所以本文将径向基神经网络用于旋转机械实现故障诊断，使用Matlab软件编程并得出识别结果.

1 径向基函数神经网络算法

RBF网络结构如图1所示.输入层到隐层为权值为1的固定连接，隐层到输出层为权值为W 的线性链接.隐层神经元基函数常采用高斯型径向基函数.

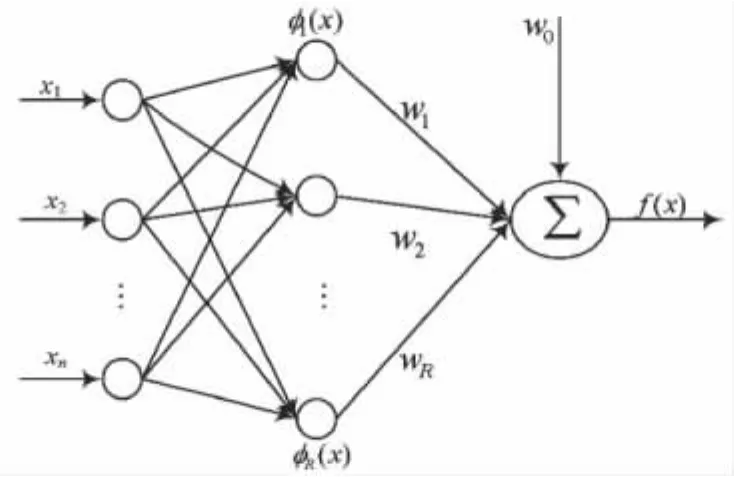
图1 RBF网络结构

隐层函数：

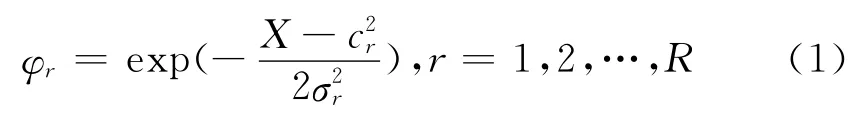
输出层函数：

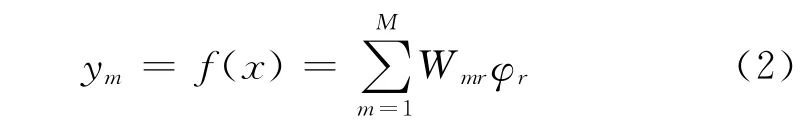
式中，cr为第r个隐层节点的数据中心，σr是第r个隐层节点的数据方差，X是神经网络的输入向量，Wmr是隐层到输出层的连接权.

径向基神经网络算法步骤如下：

1）从输入向量中选一组初始中心值cr，初始化连接权值Wmr，计算方差值σ＝dmax／R，其中dmax是最大的距离；R是cr的数量；

2）用聚类分析中的K－NN算法求取cr和σr；

3）计算输出层权值：

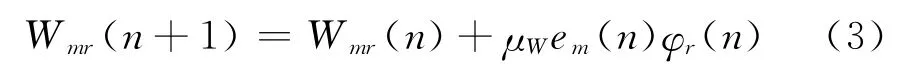
计算网络输出

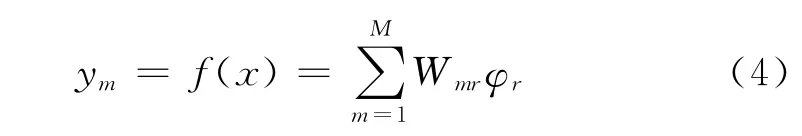
式中，em（n）＝ym（n）-dm（n），dm（n）为样本目标输出；μW是学习参数的学习步长.

4）计算网络误差并判断是否收敛.

5）若收敛，训练结束.

6）否则，更新网络学习参数cr，σr和Wmr，并转到步骤（2）［6-7］.

2 机械故障的输入和输出样本设置

本设计中可以识别的故障包括：转子不平衡，角度不对中，平行不对中，油膜涡动，油膜振荡，喘振，轴弯曲，转子松动.有的文献中，对上述故障进行诊断使用频谱能量作为特征量，难以区分角度不对中与平行不对中、油膜涡动与油膜振荡［8-9］；有的文献中，对上述故障进行诊断是识别轴心轨迹的特征，难以区分转子不平衡与轴弯曲、喘振与转子松动［10-11］.本文综合使用频谱能量，轴心轨迹特征作为机械故障的特征量，可以更有效地区分上述故障类型.

本设计使用MOBIUS公司的转子机械故障仿真仪器，转子转速为1800r／min，设置各种机械故障，观察振动信号频谱以及轴心轨迹.其中，角度不对中对应振动信号频谱如图2所示，角度不对中对应轴心轨迹如图3所示.

图2 角度不对中对应的振动信号频谱

图3 角度不对中对应的轴心轨迹

转子不平衡轴心轨迹为椭圆形，角度不对中轴心轨迹为香蕉形，平行不对中轴心轨迹为外八字形，油膜涡动轴心轨迹为内八字形，油膜振荡轴心轨迹为花形，轴弯曲轴心轨迹为椭圆形，喘振和转子松动轴心轨迹非常紊乱，变化不定.在本设计中，提取的轴心轨迹的特征包括：孔洞数，质心偏移程度，凹入个数，交叉点个数，各种故障对应的这些特征量见表1.

表1 转子故障对应的轴心轨迹特征量数值

孔洞数、交叉点个数和凹入个数大于10的都记为10，以防止数值过大对其他参数造成影响.质心偏移距离指图形的质心与轴心之间的距离，若质心与轴心重合，质心偏移程度记为0，若距离很大，质心偏移程度记为1.

将（0.01～0.39）f、（0.40～0.49）f、（0.51～0.99）f、f、2f、（3～5）f等6个频率段的频谱能量作为特征频率.根据频谱信号能量计算公式（5），计算各个频段频谱能量［12］.其中W 表示能量，ω1～ω2为频率范围.

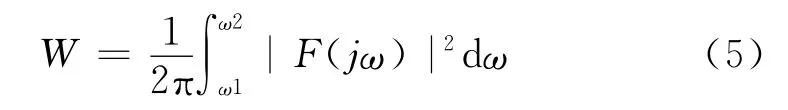
样本特征在输入神经网络之前必须进行归一化，原始的数据幅值大小不一，有时相差悬殊，如果直接使用，测量值大的波动就会垄断了神经网络的学习过程，使其不能反映小的测量值的变化.对频谱能量进行归一化处理，得到表格2前6列的数值.对轴心轨迹特征量进行归一化处理，得到表格2后4列的数值.表格2为神经网络输入样本，表格3为神经网络输出样本.

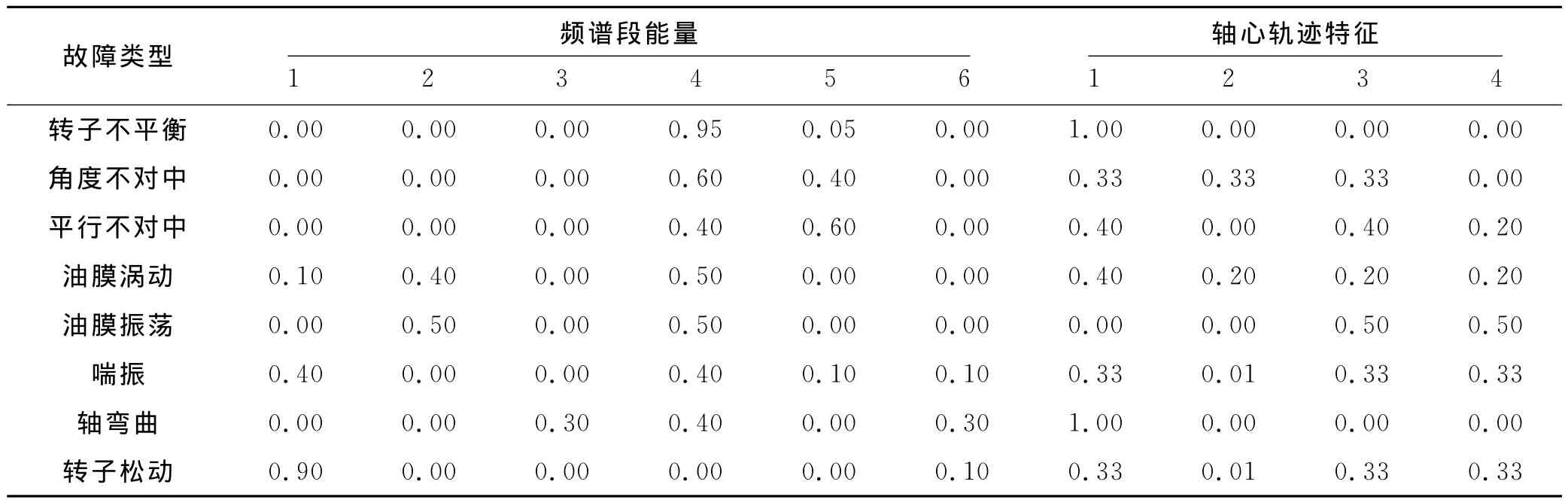
表2 神经网络输入样本

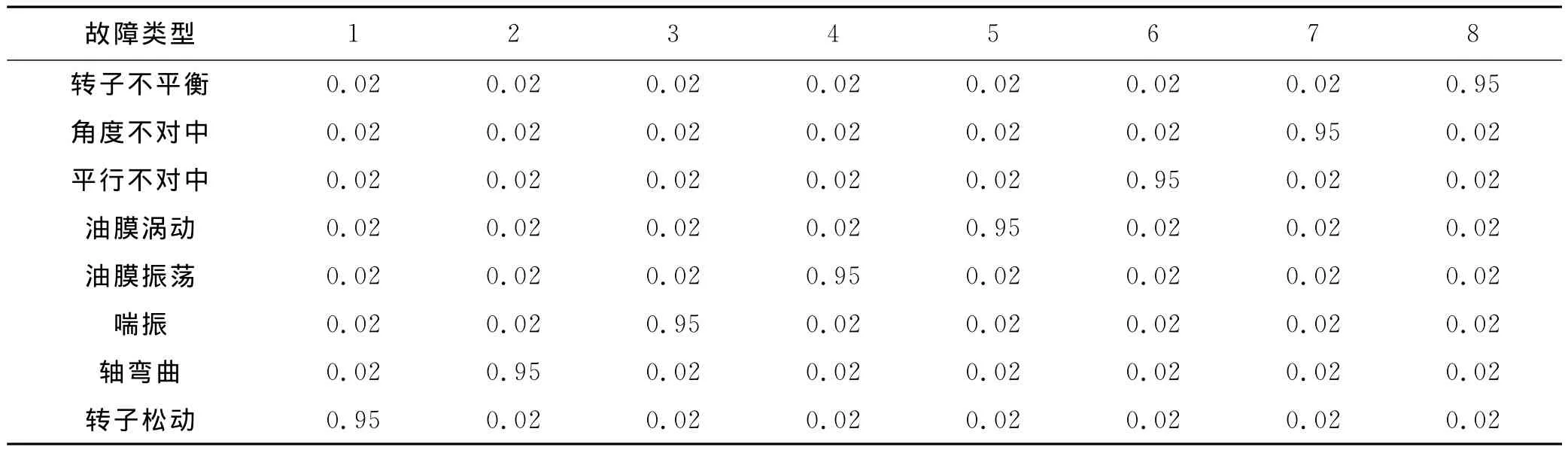
表3 神经网络输出样本

3 试验与分析

分别训练BP神经网络、Elman神经网络和RBF神经网络.BP网络分别使用trainlm、traingdx、traingd 3种训练函数进行试验，trainlm为Levenberg-Marquardt算法，对于中等规模的BP神经网络有最快的收敛速度，训练中的计算量相对较少，但需要较大内存量；traingdx（自适应动量梯度下降法）为带适应学习率和动量因子的梯度递减法；traingd为梯度下降训练函数，沿网络性能参数的负梯度方向调整网络的权值和阈值.训练次数为3000，训练目标为0.001，学习速率为0.1，其中trainlm算法对应的Matlab程序如下：

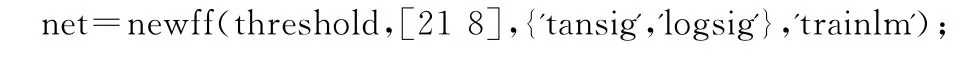
Elman神经网络训练次数为1000，训练目标为0.001，对应的主要程序如下：

RBF神经网络对应的主要程序如下，其中GOAL为均方误差，SPREAD为径向基函数的分布密度，神经元的最大数目为10，两次显示之间所添加的神经元数目为1.

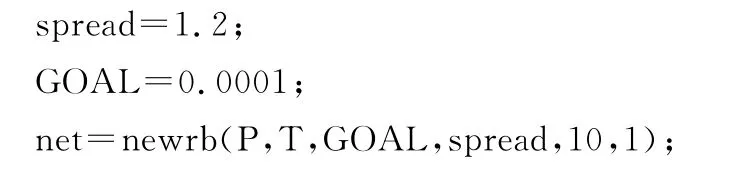
对每个网络的识别能力进行测试，输入转子不平衡、角度不对中、平行不对中对应的特征量数据：

使用RBF神经网络识别结果为：

将网络输出与各模式阈值进行比较，如果输出结果大于预设阈值，则此故障发生，否则不发生该故障.本例中，阈值设为0.9，由网络输出结果，可以看出，3个故障模式对应节点的输出与待识别样本的故障类型一致.从图4可以看出训练误差为7.21995×10-30，训练步数为7步.使用norm函数计算出识别误差为0.0243.

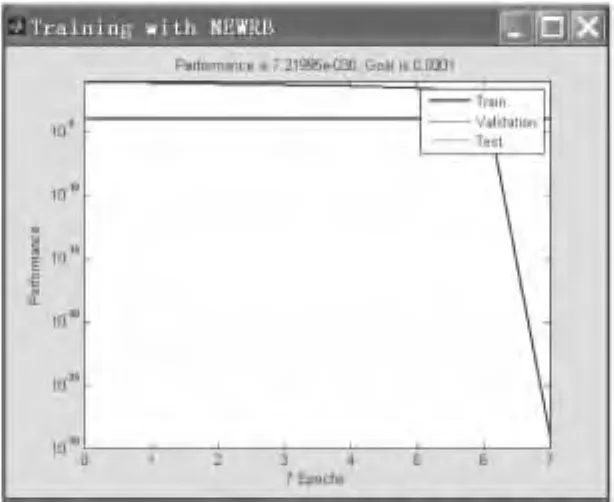
图4 训练误差与步长

各种神经网络对应的训练次数，训练误差，识别误差见表4.

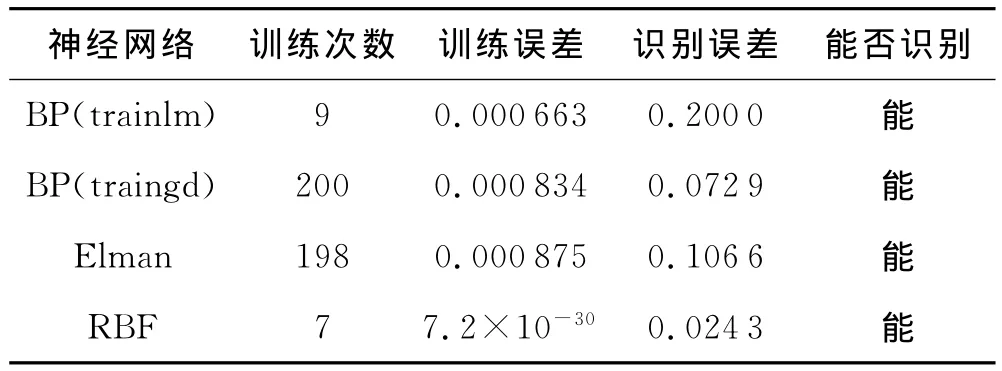
表4 各种神经网络的性能

4 结 论

1）使用Matlab编程，得出识别结果，比较了几种神经网络在机械故障识别中的性能.使用BP神经网络，trainlm学习算法可以识别，训练次数少，仅9次；traingdx学习算法训练次数多；traingd训练3000次，没有识别.Elman神经网络计算次数多，时间长.RBF神经网络，训练次数少，速度快，准确度高，识别误差小.

2）使用频谱能量和新的轴心轨迹特征作为机械故障的特征量，提供的信息更全面，可以有效地区别各种故障类型.

［1］邓 堰.转子故障智能诊断中的特征提取与选择技术研究［D］.南京：南京航空航天大学，2008.

［2］张 键.机械故障诊断技术［M］.北京：机械工业出版社，2012.

［3］沈庆根，郑水英.设备故障诊断［M］.北京：化学工业出版社，2009.

［4］鲍久圣.BP神经网络在机械故障诊断中的应用［J］.现代制造工程，2005（1）：113－114.

［5］陈法法，汤宝平，黄庆卿.免疫遗传优化Elman神经网络的旋转机械故障诊断［J］.重庆大学学报，2012（5）：7－13.

［6］汪庆华，王敬涛，邓东花.基于径向基神经网络的旋转机械故障诊断［J］.现代电子技术，2010（18）：141－142.

［7］田景文，高美娟.人工神经网络算法研究及应用［M］.北京：北京理工大学出版社，2006：41－43.

［8］肖 坤，原思聪，王 丹.SOM神经网络在旋转机械故障诊断中的应用［J］.机械设计与制造，2010（11）：44－46.

［9］栾美洁，许飞云，贾民平.旋转机械故障诊断的神经网络方法研究［J］.噪声与振动控制，2008（2）：85－87.

［10］肖圣光.基于虚拟仪器的轴心轨迹分析仪的研制［D］.重庆：重庆大学，2009.

［11］周训强.旋转机械轴心轨迹的提纯、特征提取与自动识别研究［D］.重庆：重庆大学，2010.

［12］曾禹村.信号与系统［M］.北京：北京理工大学出版社，2010.