基于SPH方法的液体晃动数值模拟

方 政 李 煜 兰庆琳 周玲玲

（河海大学 力学与材料学院，南京 210098）

液体晃动［1］是指容器内的液体由于外加扰动而产生的带有自由表面波动的运动.在很多工程领域存在液体晃动问题，例如：升船机的承船厢内水体波动、水库中水体由于地震引起的晃动以及贮液箱体内流体的晃动等.

早期研究液体晃动大多采用线性理论，即将水体简化为单摆系统.当液体晃动幅度较小时，简化模型的模拟效果较好.但随着晃动幅度增加，会产生非线性效应，自由液面难以用线性理论精确地预测出来.目前研究大幅晃动问题，多采用数值模拟方法.Har－low最早提出MAC法［2］，并首次将其应用到模拟大幅晃动问题中.Liu等应用VOF法模拟了带破碎自由液面的非线性晃动问题［3-4］.另外，边界元法、有限元法也被广泛的应用［5-6］.但是 MAC方法计算时需要的存储空间大，计算时间长［7］；VOF法难以精确的得到自由液面的位置［8］.边界元法、有限元法等在计算大变形问题时，网格会出现畸形，影响计算精度［7］.光滑粒子流体力学方法（Smoothed particle hydrodynamics，SPH）［9］是一种拉格朗日描述下的无网格粒子法.它不需要事先划分网格，能够适应大变形问题［10］.此外，SPH采用显式的状态方程计算压力，显式的时间积分法求解控制方程，能够提高计算效率.因此比较适合模拟带有自由液面的大幅晃动问题.

1 基本理论

光滑粒子流体力学（SPH）是一种无网格粒子化的数值模拟方法，其控制方程是拉格朗日型的Navier－Stokes方程组.该方法的基本思想是将计算域内流体离散成若干个粒子，并赋予每个粒子物理特性，例如，密度、质量、速度等；然后将描述这些物理特性的函数及其导数用核函数积分近似，得到这些函数的核近似方程；将核近似方程代入拉格朗日型的N-S方程组，得到粒子运动的常微分方程组；最后，采用显示积分法求解得到粒子的各物理量.

1.1 SPH中函数的近似方法及控制方程

SPH方法中，利用核函数将任意函数f（x）进行积分近似，即核函数近似

式中，Ω为包含x的积分域，W 为核函数（也称为光滑函数），h为定义核函数影响区域的光滑长度.

SPH方法模拟流体运动的过程中，光滑函数［11］影响着函数积分近似的准确性，决定了函数表达式的计算精度和效率.由于高斯型函数［12］充分光滑、稳定并且精确度较高，所以本文采用高斯型函数，表达式为

式中，R 为粒子间的相对距离；αd＝1／πh2.

拉格朗日型的N－S方程组包括连续性方程和动量方程，粒子化后得连续性方程

式中，ρi为粒子密度；N为粒子i支持域内的粒子总数；mj为粒子质量；vij为中心粒子与支持域内粒子的速度差，vij＝vi-vj；β为坐标分量.

动量方程

式中，vi为粒子速度；α，β 为左边分量；pi，pj分别为中心粒子压强和支持域内其他粒子压强；μi，μj为粒子的粘性系数为剪应变率，具体如下式：

1.2 SPH的模拟精度

实际上，SPH模拟方法是用弱可压缩性流体模型代替不可压缩流体，因此加入了人工可压缩率.这种人工可压缩率引起的误差是O（M2）（M为马赫数，M＝v／c；v为流场中速度最大值；c为模型声速）.模型中的压力按照可压缩流体的状态方程计算.

式中，c为模型声速；ρ0为参考密度；γ是常数，取为7［9］；ρ为实体粒子密度.

由上述可知模型声速影响着模拟精度，模型声速既要保证使人工可压缩流体的特性与真实流体充分接近，同时也不宜过大，以保证时间步的增量在容许范围之内.一般采用下式确定c值［9］

式中，c为模型声速；vb为整体流速；δ为相对密度差；υ为动力粘滞系数；F为体积力；L为特征长度.

2 SPH的边界处理方法

2.1 自由表面处理

SPH方法在处理自由表面时，由于粒子数量不足，计算得到的粒子密度会小于实际值，这样在利用状态方程计算压强时，得到的结果会与实际值不符，影响计算的精确度［13］.因此，需要采取一定的方法，首先捕捉到自由表面的粒子，然后赋予这些粒子水的标准密度值，从而保证计算的稳定性.

通常，若粒子密度满足Koshizuka条件［14］，即被看作是自由表面粒子.公式为

式中，ρ为粒子密度的计算值，β为小于1的参数，一般在0.8到0.98之间取值.对于弱冲击性流动，在计算出的密度稳定性较好的情况下，利用（7）式追踪自由表面粒子效率较高，模拟精度较好.由于液体有限振幅下的晃动属于弱冲击性流动，本文采用该方法处理自由表面.

2.2 固体边界

SPH方法处理固体边界问题时，比较常用的有边界排斥力法和镜像粒子法.

Monaghan提出了边界排斥力方法［15］，即在固体边壁上布置一系列的边界粒子，这些虚拟粒子会给靠近它们的实体粒子一个沿轴向的排斥力，以达到防止实体粒子穿透边界的目的.计算排斥力的公式

式中，D为常数，一般与流域速度最大值的平方量级相当；r0为截止距离；rij为边界粒子指向实体粒子的矢径；xij为边界点与实体粒子矢径的坐标分量；n1，n2为常数，通常分别取为12和4.实际模拟中，边界排斥力法有时不能完全阻挡实体粒子穿透边界，并且边界排斥力会对实体粒子产生扰动，影响计算的准确性.镜像粒子法［16］弥补这样缺陷，其基本思想是：当内侧实体粒子到边界的距离小于κhi时，在边界外侧布置与之对应的虚粒子，这些虚粒子和实体粒子到边界的距离相等，质量、密度、压力一样，速度大小相等，垂向速度相反，切向速度相同，如图1所示.另外，镜像虚粒子可以提高边界处压力计算的精确度，所以两者往往结合使用.本文采取两者结合的方法处理固体边界.

图1 粒子分布示意图

3 箱内水体晃荡模拟

采用矩形箱体，尺寸如图2所示，箱体长度L＝0.8m，箱内水深为h＝0.3m.对其进行自由晃动和一阶模态晃动的数值模拟.

3.1 自由晃动

将计算区域剖分成个80×30＝2400个实体粒子，粒子初始速度v0，粘性系数为v＝1.0×10-6m2／s.箱体不受外部激励影响，横向加速度为零，仅受重力影响，重力加速度g＝9.81m／s2.为防止实体粒子穿透边界，采用排斥力边界和镜像粒子法，在边界上布置183个虚粒子.时间步长Δt＝1.0×10-4s，采用蛙跳积分法.初始时刻，压强按静水压强分布；然后根据状态方程（5）反算出粒子密度，计算过程中始终用状态方程计算压强.

模拟时，先施加一个水平方向的加速度a′x，大小为2.4525m／s2，计算达到稳定时，形成倾斜液面，然后去掉a′x，使其只在重力作用下形成自由晃动.倾斜液面如图2所示.

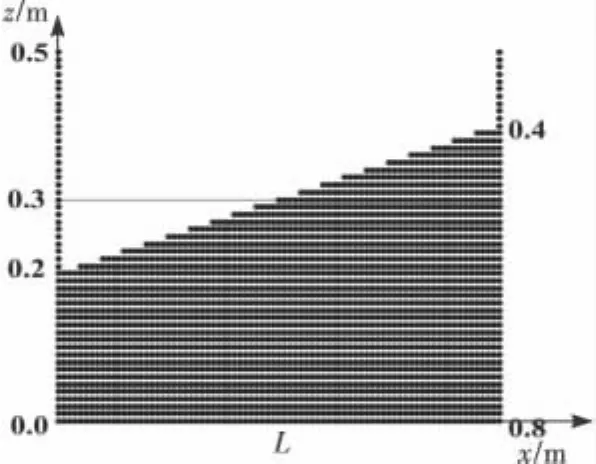
图2 贮箱尺寸及倾斜液面示意图

图3给出了x＝0m和x＝0.8m处的液面波动情况，计算得到晃动周期T＝1.051s，频率f＝0.9509Hz.根据势流理论［17］所得固有频率为0.9520Hz.结果相近，说明本文建立的数值模型较为合理，用来模拟液体晃动是可行的.

图3 x＝0.0m和x＝0.8m处液面波动

3.2 一阶晃动

对静止的液体施加横向的外部激励：ax＝-bω2sin（ωt），b为外部激励引起的震荡幅值，本文取为0.062m，ω取为5.611.其他参数及计算方法均与上例相同.计算10s工况，共耗费机时535.6s（cpu time）.

图4是不同时刻自由液面形状，从图中可以看到，一阶工况下，各时刻的自由液面围绕着液面中心点来回晃动，在中心点处的振幅大致为0m，在贮箱的一侧产生波峰，在另一侧产生波谷，这是最基本的非对称波动.

图4 不同时刻液面形状示意图

图5为x＝0.8m处自由液面的波动时程，可以看到，SPH方法得到的数据与文献［18］中的实验数据吻合较好.从图5中可以较明显地看出振动波形关于自由液面不对称，根据线性理论，只有一、二阶晃动叠加时，才会出现这种情况.这是大幅晃动中的非线性现象之一.

图5 x＝0.8m处自由液面的波动时程

图6是右边壁距离箱底0.2m处的压强时程图，图中的静水压强是指某一时刻右边壁相对于自由液面的静水压强分布.可以看出在2.2s之前，吻合较好，随着时间推移瞬时压强呈现出脉动的现象，并且与静水压强相比数值相差较大，但总体在一个合理的范围内，这也是由于水体的大幅晃动而产生的非线性现象.此外，在某些波峰和波谷处出现了二次谐波，这是由于壁面对流体的阻滞作用，产生了局部回流的原因.

图6 右边壁距离箱底0.2m处的压强时程图

4 结 语

采用SPH方法模拟了贮箱内液体大幅晃动，计算结果与相关实验数据吻合较好.分析了自由晃动和一阶晃动的液面波动和压强分布，说明本文数值模型设定的参数较为合理，显示了SPH方法在模拟液体晃动方面的优越性.

［1］曾江红，王照林.航天器液体晃动动力学的研究方法概述［J］.强度与环境，1997（4）：37－43.

［2］Harlow F H，Welch J E.Numerical Calculation of Time－Dependent Viscous Incompressible Flow of Fluid with Free Surface［J］.Physics of Fluids，1965（8）：2182－2189.

［3］Liu Dongming，Lin Pengzhi.A Numerical Study of Three－Dimensional Liquid Sloshing in Tanks［J］.Journal of ComputationalPhysics，2008，8（227）：3921－3939.

［4］郭红民，向光明，谢 洋，等.毛家河水电站溢洪道三维数值模拟［J］.水电能源科学，2013，31（3）：81－85.

［5］Nakayama T，Washizu K.The Boundary Element Method Applied to the Analysis of Two－dimensional Nonlinear Sloshing Proble［J］.International Journal for Numerical Methods in Engineering，1981，17（11）：1631－1646.

［6］曹宗杨，张燎军.拱坝-库水动力流固耦合作用的有限元数值研究［J］.水电能源科学，2013，31（4）：58－61.

［7］陈海舟.不可压自由表面流的SPH法数值模拟研究［D］.天津：天津大学，2008.

［8］Hirt C W，Nichols B D.Volume of Fluid（VOF）Method for the Dynamics of Free Boundaries［J］.Comput.Phys，1981，39：201－225.

［9］Liu G R，Liu M B.Smoothed Particle Hydrodynamics－a mesh free Particle method［M］.Hong Kong：World Publishing Company，2005.

［10］杜小弢，吴 卫，龚 凯，等.二维滑坡涌浪的SPH方法数值模拟［J］.水动力学研究与进展（A 辑），2006（5）：579－586.

［11］Gingold R A，Monaghan J J.Smoothed Particle Hydrodynamics：Theory and Application to Non－Spherical Stars［J］.Monthly Notices of the Royal Astronomical Society，1977，181：375－389.

［12］Monaghan J J，Lattanzio J C.A Refined Particle Method for Astrophysical Problems［J］.Astron.Astrophys，1985，149：135－143.

［13］何 涛，周 岱.二维自由表面流动的光滑粒子动力学方法数值模拟［J］.上海交通大学学报，2011（10）：1425－1429.

［14］Koshizuka S，Nobe A，Oka Y.Numerical Analysis of Breaking Waves Using the Moving Paticle Semi－Implicit Method［J］.International Journal for Numerical Methods in Fluids，1998，26：751－769.

［15］Monaghan J J.Simulating Free Surface Flows with SPH［J］.Journal of Computational Physics，1994，110（2）：399－406.

［16］Randles P W，Libersky L D.Smoothed Particle Hydrodynamics：Some Recent Improvements and Applications［J］.Computer methods in applied mechanics and engineering，1996，139：375－408.

［17］Faltinsen O M.A Nonlinear Theory of Sloshing in Rectangular Tanks［J］.Journal of Ship Research，1974，18（4）：224－241.

［18］Antonio Huerta，Wing Kam Liu.Viscous Flow with Large Free Surface Motion［J］.Computer Methods in Applied Mechanics and Engineering，1988，69（3）：277－324.