最小费用最大流在线性规划上的推广

任孝忠，韩震华

(四川省工业贸易学校 公共课教研室，成都 610081)

1 引例［1－2］

某地区的河流从一源点开始向外流出，在某些城市上分成若干份，成树形分布，共有m个支流，每一支流河流分别受到不同程度的污染w［i］。若现有n个治理方案，每个方案均需要沿河流的连续城市共同处理，每个方案有一个最大执行力度上限l［i］，每单位执行力度需要消耗 c［i］的财力，并可取得一单位的污染治理成果。设计一种安排方案使得在治理完所有污染的前提下的总计财力花销最小。

例:在图1中，城市1到城市2的支流需3单位执行力度的治理，城市1到城市3的支流需1单位执行力度的治理，城市3到城市4的支流需2单位执行力度的治理;从城市1到城市2的治理方案有执行力度上限4，单位执行力度消耗1单位的代价;从城市1到城市4的治理方案有执行力度上限2，单位执行力度消耗2单位的代价。

图1 有向图

2 问题分析［3－4］

设列向量x，其中x［i］表示第i个治理方案的执行力度;设矩阵A，A［i］［J］表示第一个支流是否被第j个治理方案包括。将c行向量化，l和w列向量化。则本问题可以表述为以下线性规划问题:

因此对于图1有:

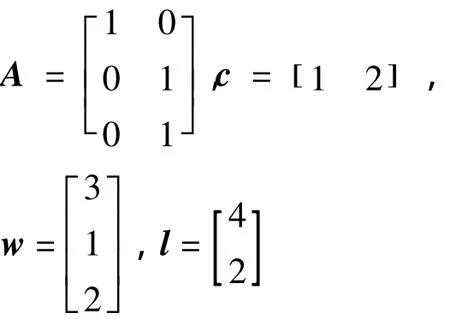
对于这样的问题，传统方法是使用线性规划来解决，然后由于线性规划的算法效率较低，往往在实际应用中受到诸多限制。

3 算法优化

3.1 (点边)关系矩阵［5］

此时，关系矩阵具有以下性质:每一列有且仅有一个1与 －1(适合有向图)。

对于本问题，矩阵A不能视作一个图的关系矩阵，因此，需要做对应的矩阵变换。

3.2 矩阵变换

首先，考虑将不等式Ax≥w的不等号去除掉。

对矩阵和向量进行以下设定:

其中，向量y为上界差值，通过这些设定使得A'成为(m+1)×(n+m)规格的矩阵。

可以注意到新增的列与矩阵A中原始的行存在一一对应关系。于是可写成等式A'×x'=w'。

这样，我们通过引入上界差值y，将不等号表述为等号。

根据图1，设矩阵A'及向量c'，w'，l'具有以下数值:

当约束条件变为A×x＜w时，只需将A'中的－i变成i即可。

继续做行变换，得到A″和w″满足以下条件:

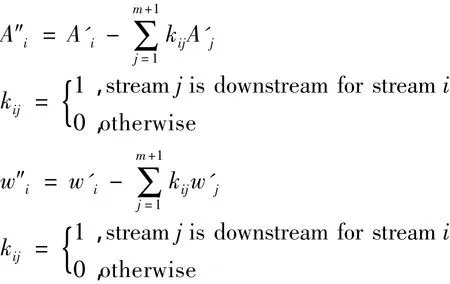
我们可以尝试从图论角度理解该问题。该变换的实质即为，对每一条支流所对应的行与其下游支流所对应的行相减。新增的行则可以抽象为所有从源点出发的支流的起源支流。这时我们分别考虑两种列，一为原始矩阵A存在的列，二为新增的列。

对于原始存在的额列，即某一治理方案，其最下游的支流所对应的行为1，最上游的支流所对应的行为－1，其余支流均为0。

对于新增的列，其对应的行为1，对应行的上游支流所对应的行为0，其余行为0。故A″矩阵中的每一列有且仅有1个1和－1。

这样，由关系矩阵的特性可知，A″可以视作某个图的点边关系矩阵，至此，我们可以通过建立最小费用流模型来解决此问题。此时，图1中的矩阵A和向量w经过转换后得到如下所示的A'和w'。

3.3 最小费用流

针对以上问题分析验证可发现，最小费用流能够解决的问题可以用以下形式表示:

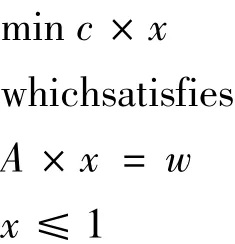
其中，A为关系矩阵;c为边的单位流量费用向量;x为边的流量列向量;w为点的平衡条件;1为边的流量上界列向量。显然，经过转换的矩阵满足上诉条件，显而易见，可以使用最小费用流方法来解决。

最小费用流的常见解决办法主要有消负圈［6］和连续最小费用增广路，其复杂度上界均为O(max f×n×m)，因此，并不是严格的多项式算法。而在以往的研究中，确实存在一些严格多项式算法复杂度的最小费用流方法［7］。

但是，正如同在线性规划问题中，最普通的单纯形法的效率往往比严格多项式算法更高，对同一个问题用最小费用流的求解速度远远快于用线性规划的速度。

这样，我们就得到了一个很好地在类多项式时间内解决该问题的算法了，那么，什么样的问题可以用该算法来解决呢?

4 结论

从线性规划的角度讲，如果约束矩阵的每一列是由若干连续的1组成的，那么该问题即可以解决。我们令矩阵A″满足下列条件即可:

显然，这时矩阵A″每一列仅有一个1和－1。

从问题的原始描述角度上讲，如果问题是对某一连续区间产生的影响，那么该问题统一可以用此方法解决。可令矩阵A″满足:

即可将原问题转化为可使用最小费用最大流解决的问题形式。

5 结束语

采用传统的线性规划解法和最小费用流算法对图1所示的问题进行编程实验验证，两种算法皆采用C语言编写实现。对于线性规划解法，采用了运行速度较快的单纯形法［8］，得到了如下结果:

而采用最小费用流算法得到了如下结果:

通过验证发现，采用最小费用流算法的效率提升了47倍，如果把读入时间考虑进去，实际的效率提升会更大!该算法的重要性和意义也不言而喻。可以预见，该算法在实际应用中还有很多值得推广和进一步研究的空间。

［1］Ravindra K Ahuja，Thomas L Magnanti，James B Orlin.Network flow:theory，algorithms，and applications［M］.Beijing:China Machine Press，2005:602－604.

［2］李凯镇 .River Problem［EB/OL］.［2013－04－21］.http://acm.hdu.edu.cn/showproblem.php?pid=3947.

［3］刘汝佳，黄亮.算法艺术与信息学竞赛［M］.北京:清华大学出版社，2004:319－320.

［4］刘汝佳.算法竞赛入门经典［M］.北京:清华大学出版社，2009:211－212.

［5］Douglas B.West introduction to graph theory［M］.Beijing:China Machine Press，2006:367－368.

［6］Andrew V Goldberg，Robert E Tarjan.Finding minimumcost circulations by canceling negative cycles［J］.Journal of the ACM(JACM)，1989，36(4):873－886.

［7］James B Orlin.A faster stronglypolynomial minimum cost flow algorithm ［J］.Operations Research March/April，1993，41(2):338－350.

［8］James P Ignizio，Tom M Cavalier.Linear programming［M］.USA:Prentice－Hall，1994.