Nb基合金中氧原子扩散及团簇化的第一性原理

祝令刚，胡青苗，孙志梅，*

1.北京航空航天大学 材料科学与工程学院，北京 100191

2.中国科学院金属研究所，辽宁 沈阳 110016

随着对发动机推力的要求越来越高，提高燃烧气体温度和燃料利用率势在必行。当前实际应用的涡轮叶片为Ni基高温合金，其使用温度达到1 150℃，低于其熔点200℃。对于Ni基材料的叶片，如果燃气温度进一步提高，需要依赖更好的隔热涂层和冷却方法防止叶片过热甚至融化，然而冷却叶片意味着能量白白的损耗。另一个选择是寻找能够替代Ni基合金的材料。受苛刻服役环境的限制，潜在的替代材料首先要满足高熔点，以及高的抗蠕变性能。陶瓷材料、金属间化合物和难熔金属是有可能的替代材料。它们各自有优缺点：陶瓷和金属间化合物有比强度高以及抗氧化的优点，但其低温脆性使其难以加工，且较低温度区间工作时容易失效；难熔金属在加工方面有其优势，但最大的问题是自身的抗氧化性能差，远远不能满足高温合金的服役要求。在难熔金属中备受关注的是Nb，熔点为2 469℃［1-2］。

对于纯金属Nb，氧化时环境中的氧穿过氧化膜向内扩散导致持续氧化。在氧化的初始阶段，形成保护性的氧化膜Nb2O5，随着氧化膜的生长，氧化物在氧化膜-金属界面生成，在氧化膜中产生内应力，应力的积累可导致氧化膜的开裂，并导致“失稳”的线性氧化规律。例如在600℃ 氧化时，初始阶段，氧化膜的生长遵从抛物线规律，利用声发射技术原位测量时，未发现氧化膜开裂现象，但15 min后，声发射探测到氧化膜发生了明显的开裂，氧化动力学迅速变成了线性规律，因此纯Nb显然不能在高温下长期暴露［2-3］。

添加合金元素是提高基体抗氧化性的重要途径，一般情况下Al、Cr、Si为常用元素，因为它们的氧化物Al2O3、Cr2O3、SiO2具有良好的稳定性和对基体的保护性。每种氧化物发挥保护性的温度区间和有效工作环境是有限定的：对于Al2O3而言，在温度低于1 300℃ 时生长速度较慢；温度更高时SiO2的保护性更加有优势，但SiO2在低温低氧压下可与Si反应生成极具挥发性的SiO；对于Cr2O3而言，高温高氧压下与氧进一步反应生成挥发性的Cr2O3，使氧化膜不断减薄，除此之外，Cr2O3在恒温下容易发生起皱和破裂，主要是由生长应力引起的，1 200℃左右金属Cr表面的Cr2O3即丧失保护性。虽然这3种保护性的氧化物都有缺陷，但是目前仍是设计耐热氧化合金时的主要选择［2］。

为了优化氧化膜结构并进一步提高Nb的抗氧化性能，基体中要添加更多的合金元素。20世纪50年代，Sims等［1］研究了各种二元合金Nb X（X=Ti，V，Zr，Al，Cr，Co，Fe，Mn等）的氧化行为，发现Ti对氧化性能的提高最为明显，而且当Ti的含量达到25at% 时，生成的氧化物也只有Nb2O5；1 300℃ 下，Nb可以溶解8at% 的Al，氧化产物仍为Nb2O5。如果要在Nb合金中生成保护性的氧化膜Al2O3，Al的原子分数需要达到40%，此时体系中会生成大量的金属间化合物Nb Al3和Nb Al2等，这些金属间化合物可以为Al2O3的生长提供Al元素。Murakami等［4］发现Nb-47Si-20Al合金（主要为 Nb3Si5Al2相）在1 023 K氧化时形成了保护性的Al2O3，大大提高了合金的抗氧化性能。同样对于Nb-Si合金，体系中的组织多为两相，一相为Nb基固溶体，另外一相为化合物Nb5Si3，且后者占有相当高的体积分数，通用电气的Bewlay等［5］在Si原子分数为16%的多元素Nb合金中发现Nb5Si3的体积分数高达46%。对于Nb-Si基合金，若要使其在氧化中生成保护性SiO2，Si的含量要求很高。Cheng等［6］在 Nb-（34at%）Si-（10at%）B 的氧化物中发现了晶态但仍然不连续的SiO2，产物主要还是Nb2O5。可见对Nb合金抗氧化性的提高仍然还有很多问题需要解决［2］。

Nb基合金除了可以作为高温结构材料，在Snoek型阻尼材料应用方面也有些报道［7-9］。在外界冲击等作用力下，阻尼材料中的间隙原子如氧原子等，发生跳跃迁移，从而消耗外力对基体的影响。实际中可通过添加合金元素，改变间隙原子在基体中的扩散激活能，从而达到改善阻尼合金性能的目的。

从原子尺度上理解上述两种应用背景下Nb合金的材料科学问题是十分复杂的，尤其是氧化问题，涉及氧原子的扩散和聚集、氧化物的形核长大、多层氧化物以及氧化物与基体之间的结合等过程。基于密度泛函理论的第一性原理计算虽然在时间和空间尺度上均不能完整地描述合金的氧化或阻尼过程，但对复杂过程中涉及的细节问题是可以独立出来精确处理的，比如氧原子在金属基体中的扩散问题［10］、氧化初期基体表面氧化物前驱体的结构［11-13］、基体与氧化物界面的结构和强度等［14-15］。这些问题的第一性原理计算研究，除了为实验现象提供物理图像外，对更接近实际过程的大尺度计算模拟也提供着基本数据的支持，同样对计算模拟辅助材料设计有重要的意义。

基于上述考虑，本文利用第一性原理计算首先研究了氧原子在基体Nb中的扩散问题，作为潜在的发动机叶片材料，Nb基合金服役环境中不断受到应力作用，考虑了单轴应变下氧原子扩散行为的变化；研究了氧原子在Nb中形成原子对的倾向性，以及合金元素Ti和Zr对其的影响。

1 计算参数设置

采用奥地利维也纳大学开发的第一性原理VASP（Vienna Ab-initio Simulation Package）软件包［16-17］进行计算。电子间的交换关联泛函采用广义梯度近似PW91-GGA［18］。电子与原子核的相互作用通过PAW赝势［19］描述。为了保证计算的精确性，这里对于涉及的过渡金属原子Nb、Ti和Zr，其内层p电子也被处理成价电子。平面波截断能设置为300 eV，k点网格为4×4×4。计算过程中费米能级附近展宽采用Methfessel-Paxton方法，宽度为0.2 eV。对于纯Nb，计算得到的晶格常数为3.321Å，与实验数据的3.307 Å［20］符合较好。模拟合金用的超晶胞为3×3×3，包含54个原子，考虑合金结构时，其中1个Nb原子被置换，这样所模拟的合金的浓度为1.85%。

对于氧原子在Nb中的扩散，采用NEB方法（Nudged Elastic Band Method）［21］得到扩散路径和势垒。使用NEB方法时要先得到扩散前后对应的2个结构，即初始态和终了态；在2个态之间线性插值得到一些中间态（Image），并建立起初始的扩散路径；在路径优化过程中，平行于路径方向上人为施加弹簧力（Spring Force），以保证中间态不会弛豫到初始或终了结构；优化完成后要使各中间态在垂直于路径方向的分力为0。本文计算过程中选取了4个中间态，NEB计算收敛标准为各中间态原子上的力小于0.05 e V/Å。这里考虑了在［001］方向施加单向应变时氧原子扩散行为的变化，为得到施加应变后超晶胞的结构，计算过程中固定单方向的晶格常数，其他两个方向自由弛豫。

2 计算结果与讨论

2.1 单向应变下氧原子的扩散

本部分计算了氧原子在施加单向应变的体心立方Nb中的扩散。如图1所示，应变为0时（S=0），八面体间隙1、2和3是等同的，此时氧原子在任意相邻八面体间隙之间的扩散均是等价的，势垒大小为0.92 eV，与实验值1.11～1.14 e V［22］符合较好；而且扩散路径为直线，过渡态结构为氧原子占据两八面体间隙之间的四面体间隙位置，即扩散势垒的大小可以理解为氧原子占据八面体间隙和四面体间隙时对应体系的能量差［23］。施加的单向应变大小为0.02、0.04、0.06、0.08和0.10，方向如图1中箭头所示。施加单向应变后，八面体间隙均会发生畸变，但间隙1和间隙2仍是等价的，计算发现氧原子在这2个间隙之间扩散的势垒随着应变的增大而不断减小，如图2（a）所示，也就是说施加应变后氧原子占据八面体间隙和四面体间隙时对应体系的能量差不断减小。反应坐标（横坐标）显示出2个间隙之间的距离随着应变的施加而逐渐被拉开。

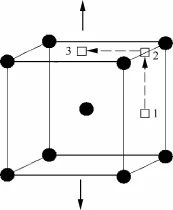
图1 单向应变下氧原子在Nb中的扩散路径Fig.1 Pathways for oxygen atom diffusion in uniaxialstrained Nb

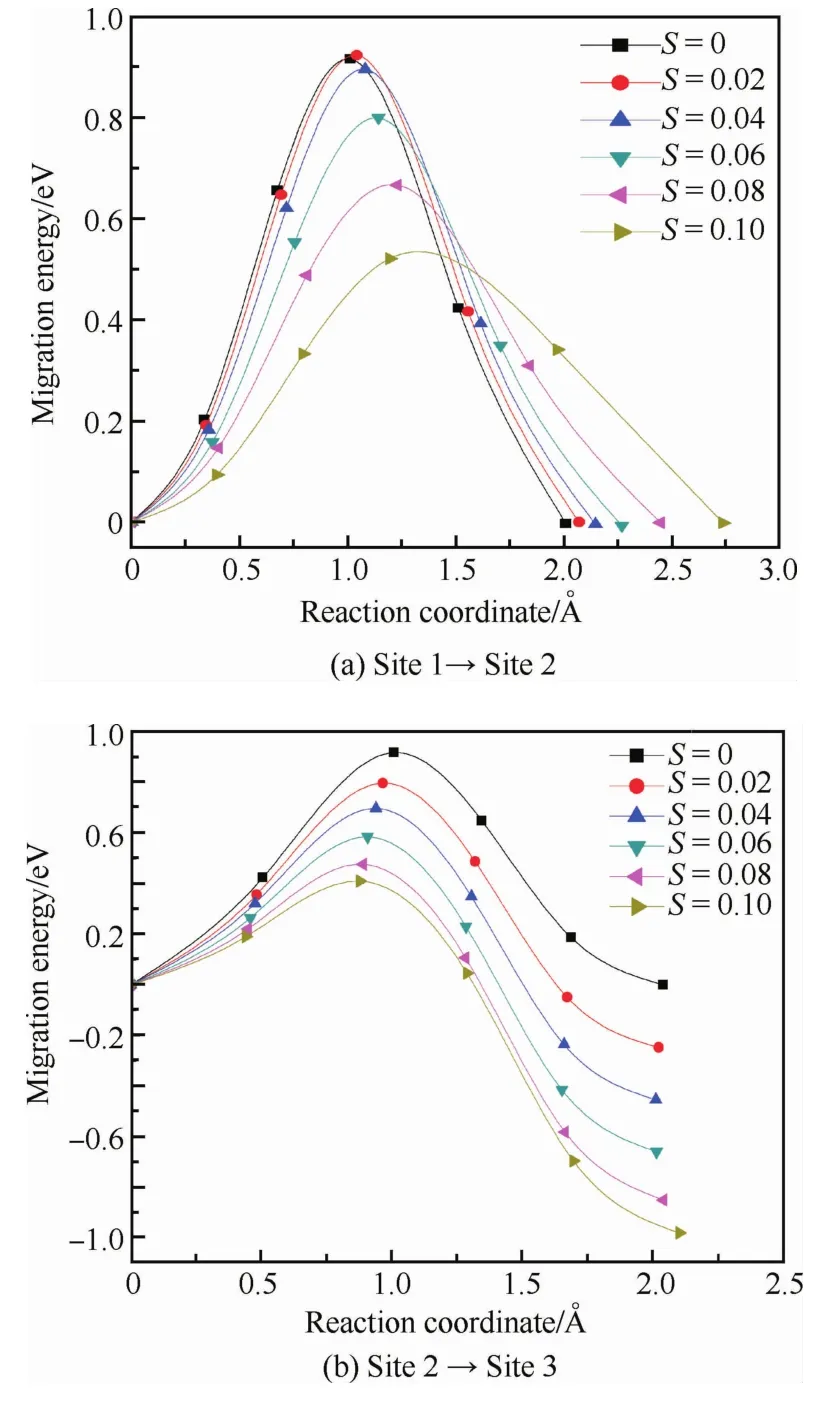
图2 不同单向拉伸应变量下氧原子扩散的势垒曲线Fig.2 Barrier curve of oxygen atom diffusion under different uniaxial tensile strains

间隙2和间隙3在应变作用下不再等价。对于间隙2，扁八面体的2个顶点距离进一步被压缩，而间隙3相应的2个顶点间距不断拉长。可以想象间隙3更适合氧原子的占据，这从图2（b）中的扩散势垒曲线可以直接反映出，扩散前后体系的能量变化随着应变的增大而变大，氧原子更倾向占据间隙3。间隙2到间隙3的扩散势垒随着应变的增大而变小，即从动力学扩散的角度讲，氧原子也倾向于向间隙3偏聚。

从图2中2个扩散势垒曲线可以看出，当施加单向应变后，氧原子会以比无应变下更快的扩散速度（势垒更小）发生偏聚，而且是沿施加应变的方向排列。显然氧原子的这种偏聚会导致应力的集中，容易引起裂纹萌生，降低材料的力学性能。

2.2 Nb合金中氧原子对的形成能力

此部分讨论了2个氧原子在Nb中占位较近并形成原子对的可能性，图3给出了可能形成氧原子对的全部构型。图3中字母代表各种八面体间隙位置，这里只考虑了合金元素X的最近邻和次近邻位置，因为研究发现［9］，第3近邻位置时合金元素与氧原子的相互作用已经可以忽略不计。

图3 合金元素X周围第1和第2近邻八面体间隙位置Fig.3 First-and second-nearest octahedral interstice near alloying element X

本文中氧原子对的构型用图3中的2个字母表示，比如原子对AH表示一个氧原子位于A间隙，另一个氧原子位于H间隙的构型。这里计算氧原子形成原子对能力的方法具体为：将氧原子形成原子对的过程分成2个阶段，第1阶段（Stage 1）对应氧原子浓度很低的情况，此时氧原子都有机会在最强的吸引位置（对应体系的能量最低），即每个氧原子都可以单独“享有”一个合金原子，此时对应的形成氧原子对的能力可以用能量表示为

式中：EXOO为含合金元素和氧原子对的超胞的能量；EX为仅包含合金原子的超胞的能量；EXO为含合金元素以及单个氧原子的超胞的能量且此氧原子处于最强吸引间隙位置。第2阶段（Stage 2），对应氧浓度稍微高些的情况，此时假设每个合金原子周围已经有一个氧原子占据在能量最优的位置，此时氧原子对的能力可用能量表示为

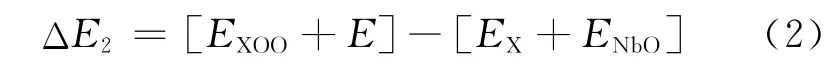
式中：E为纯Nb超胞的能量；ENbO为Nb基体中含一个氧原子时超胞的能量，可见ΔE2也表示把氧原子从基体内部移动到合金原子周围与另外的氧形成原子对时体系能量的变化。

除了纯Nb体系，这里考虑了2种合金元素Ti和Zr，之所以选择这2种合金元素是因为前期研究发现Ti对第1近邻间隙位置的氧原子作用最强，而Zr对位于其第2近邻间隙的氧原子作用最强，V与Ti的情况类似，而Hf与Zr的情况类似，即这里选择的Ti和Zr在合金元素与氧原子相互作用方面是具有代表性的［9］。Stage 1和Stage 2对应的相互作用能计算数值如表1所示，对于Stage 1，能量均为正值，表示氧原子的浓度很低时，更倾向于单独占据在合金原子附近的最低能量对应的间隙位置，不会形成原子对。对于Stage 2，Ti和Zr都出现了负值能量，表示此时氧原子会从基体移动到合金原子周围形成原子对。还可看出对于Zr，氧原子对形成的可能性更大，因其负值能量较多且绝对值较大。因此可以判定，对于合金原子为Zr时，氧原子对的形成可能性比Ti对应的情况大得多。同样可以推断X=Hf时，情况和Zr类似。

可见，加入不同合金元素之后，会对基体中氧原子的分布产生不同的影响，而氧原子的分布对应力集中，甚至是氧化物的形核都有重要作用。当然这里只计算了2个氧原子形成氧原子对的可能性，要研究对材料氧化等宏观性能的直接影响，还需进一步考虑更多的氧原子形成团簇的情况。

表1 两阶段中氧形成不同构型原子对的能力Table 1 Pairing ability of oxygen atoms into certain configurations at two stages

为进一步理解合金元素周围氧原子对形成能力不同的物理层次原因，图4（a）～图4（c）给出了不同合金成分下的电子态密度图，插图对应的能量范围为-8.5～-6.5 eV。这里以AH和BG 2种构型为例，因为此构型下氧原子分别在Ti和Zr周围配对的倾向性最大，即此2种构型具有代表性。

图4 氧原子对构型为AH和BG时对应超胞的态密度Fig.4 Density of states for superstructure with oxygen atom pair having configuration of AH and BG

从图4可以看出氧原子对组成AH和BG 2种构型时体系的态密度图差别很小，主要因为对应超胞的总能量差别较小。相对明显的差异在能级为-7.5 e V左右的态密度峰（图4中的插图），对于X=Nb和Ti，构型BG对应的此峰向高能级偏移明显，处于较高的能量水平，即BG对应构型的能量也较高，这与表1中列出的能量数据吻合。对于X=Zr时，-7.5 e V左右的峰出现了明显的分裂，BG对应峰的左侧部分仍出现了高能级的偏移（相对AH构型），但其偏移量较小，而且其右侧的分裂出来的峰出现了向低能级移动的趋势，可以看出这是导致X=Zr时BG对应的构型能量较低，而X=Nb和Ti时则不然的一个原因。

3 结 论

1）对Nb施加单向应变，即产生了被拉长的八面体间隙（在应变施加的方向被拉长）和被进一步压扁的八面体间隙，计算发现氧原子更倾向于占据被拉长的间隙中。当应变为0.1时，占位优势（能量差）达到了1.0 eV，而且向这种类型间隙扩散的速度会加快（对应的势垒减小）。应变最终导致氧原子沿应变方向偏聚排列，且随着应变的增大这种现象更加明显。

2）在纯Nb中，氧原子浓度不高时，倾向于均匀分布在基体中，无形成原子对的倾向。在元素Ti和Zr掺杂后，由于2种元素对氧原子均有吸引作用，氧原子的分布情况会类似于合金元素的分布，通常也是均匀分布在基体中的；当氧原子的浓度升高后，氧原子倾向于在合金元素周围形成原子对，原子对的形成可使体系的能量降低最多达0.29 e V。计算结果也表明，Zr比Ti更容易使得氧原子形成原子对。电子结构分析表明，态密度峰的分裂和偏移是导致形成不同构型原子对的重要原因。

参 考 文 献

［1］ Ghosh G，Olson G B.Integrated design of Nb-based superalloys：Ab initio calculations，computational thermodynamics and kinetics，and experimental results［J］.Acta Materialia，2007，55（10）：3281-3303.

［2］ Zhu L G.Theoretical study on the oxidation of Ti and Nbbased alloys［D］.Shenyang：Insititute of Metal Research，Chinese Academy of Sciences，2014.（in Chinese）祝令刚.Ti和Nb合金中氧化问题的理论研究［D］.沈阳：中国科学院金属研究所，2014.

［3］ Birks N，Meier G H，Pettit F S.Introduction to the hightemperature oxidation of metals［M］.Xin L，Wang W，translated.Beijing：High Education Press，2010：84-85.（in Chinese）Birks N，Meier G H，Pettit F S.金属高温氧化导论［M］.辛丽，王文，译.北京：高等教育出版社，2010：84-85.

［4］ Murakami T，Sasaki S，Ichikawa K，et al.Microstructure，mechanical properties and oxidation behavior of Nb-Si-Al and Nb-Si-N powder compacts prepared by spark plasma sintering［J］.Intermetallics，2001，9（7）：621-627.

［5］ Bewlay B P，Jackson M R，Zhao J C，et al.A review of very-high-temperature Nb-silicide-based composites［J］.Metallurgical and Materials Transactions A：Physical Metallurgy and Materials Science，2003，34 （10）：2043-2052.

［6］ Cheng J C，Yi S，Park J S.Oxidation behaviors of Nb-Si-B ternary alloys at 1100°C under ambient atmosphere［J］.Intermetallics，2012，23：12-19.

［7］ Yin F X，Yu L M，Ping D H.Modeling and control of the high damping behavior in Ti-Nb-O alloys［J］.Materials Science and Engineering：A，2009，521-522：372-375.

［8］ Yu L M，Yin F X，Ping D H.Natural mechanism of the broadened Snoek relaxation profile in ternary body-centered-cubic alloys［J］.Physical Review B，2007，75（17）：174105-174112.

［9］ Yu L M，Yin F X.Internal friction of Niobium-Titanium-Oxygen alloys［J］.Journal of Materials Science，2007，42（18）：7819-7826.

［10］ Zhu L G，Wang H，Hu Q M，et al.Trapping of interstitial defects：filling the gap between the experimental measurements and DFT calculations［J］.Journal of Physics：Condensed Matter，2013，25（43）：435402-435408.

［11］ Wang L，Shang J X，Wang F H，et al.Oxygen adsorption onγ-TiAl surfaces and the related surface phase diagrams：A density-functional theory study［J］.Acta Materialia，2013，61（5）：1726-1738.

［12］ Wang Q G，Shang J X，Yang Z.First-principles study on the initial oxidization of a Nb（100）surface［J］.The Journal of Physical Chemistry C， 2012， 116 （44）：23371-23376.

［13］ Todorova M，Reuter K，Scheffler M.Density-functional theory study of the initial oxygen incorporation in Pd（111）［J］.Physical Review B，2005，71（19）：195403-195410.

［14］ Zhu L G，Hu Q M，Yang R，et al.Binding of an oxide layer to a metal：The case of Ti（10-10）/TiO2（100）［J］.The Journal of Physical Chemistry C，2012，116（6）：4224-4233.

［15］ Zhu L G，Hu Q M，Yang R，et al.Atomic-scale modeling of the dynamics of titanium oxidation［J］.The Journal of Physical Chemistry C，2012，116（45）：24201-24205.

［16］ Kresse G，Furthmuller J.Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set［J］.Computational Materials Science，1996，6（1）：15-50.

［17］ Kresse G，Furthmüller J.Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set［J］.Physical Review B，1996，54（16）：11169-11186.

［18］ Perdew J P，Wang Y.Pair-distribution function and its coupling-constant average for the spin-polarized electron gas［J］.Physical Review B，1992，46（20）：12947-12954.

［19］ Blöchl P E.Projector augmented-wave method［J］.Physical Review B，1994，50（24）：17953-17979.

［20］ Ikehata H，Nagasako N，Furuta T，et al.First-principles calculations for development of low elastic modulus Ti alloys［J］.Physical Review B，2004，70（17）：174113-174120.

［21］ Henkelman G，Uberuaga B P，Jonsson H.A climbing image nudged elastic band method for finding saddle points and minimum energy paths［J］.The Journal of Chemical Physics，2000，113（22）：9901-9904.

［22］ Vykhodets V B，Kurennykh T E，Lakhtin A S，et al.Activation energy of hydrogen，oxygen，and nitrogen diffusion in metals［J］.Doklady Physical Chemistry，2005，401（4）：56-58.

［23］ Li C X，Luo H B，Hu Q M，et al.Theoretical investigations of interstitial atoms in bcc metals：Local lattice distortion and diffusion barrier［J］.Computational Materials Science，2012，58：67-70.