低速边棱音的振动特征

邸惠芳，吴胜举,2，李凤鸣，许昊



低速边棱音的振动特征

邸惠芳1，吴胜举1,2，李凤鸣1，许昊1

(1. 陕西师范大学物理学与信息技术学院，陕西西安 710119；2. 陕西省超声重点实验室，陕西西安 710119)

边棱音是一种复杂的流体动力学现象，通过数值模拟研究边棱音发声系统在射流不稳定情况下的发声特性。研究了射流速度低于湍流速度的不同流速下，簧片尖端以及两侧的旋涡、压力、速度的分布和压力特性。模拟结果显示：射流具有明显的抖动特性，在簧片两侧形成涡街、压力交替分布，基于出现的现象，初步探讨了簧片振动产生边棱音的机理。

漩涡；边棱音；压力

0 引言

边棱音[1]是由窄缝出来的气流或液流喷注遇到正对着的边棱时所发出的声音。用于工程中的边棱音发声系统(如图1所示)主要由一个喷嘴和正对喷嘴放置的楔形物(也称边棱或簧片)组成，高速射流(气体或液体)从喷嘴喷出冲击边棱，在边棱尖端处分开，在边棱上下表面形成不对称的涡街，从而发出一定强度和频率的声音，因此，也称为流体动力发声器。虽然，关于边棱音发声机理的研究已有一个半世纪的历史，但是主要集中在以空气为动力源的研究，因其流速比较低，所以在劈尖两侧能观察到明显的交替涡街。Brown[2]对空气中边棱音的研究得到“涡流导致边棱音”的结论，为后来的研究者奠定了基础。与以空气为动力源相比，由于液体的密度、声速比空气大，加之液体的不可压缩性，以液体为动力源进行发声的条件显得更苛刻，因而关于以液体为动力源的边棱音发声机理的研究甚少。

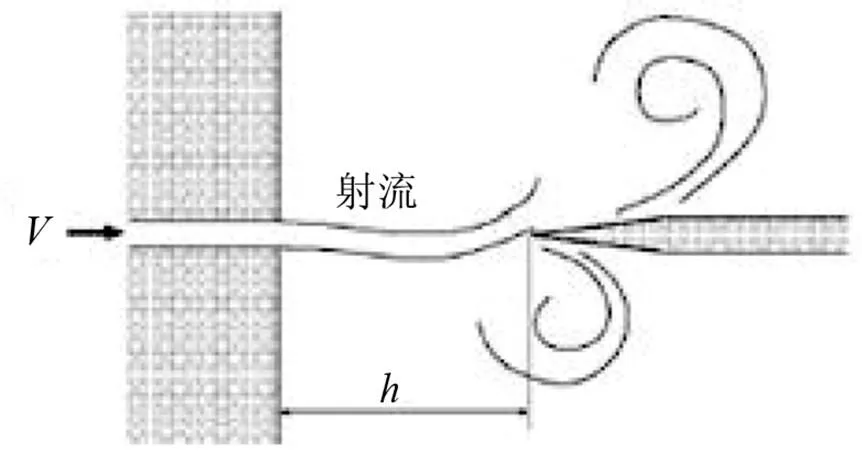
图1 边棱音发声装置的结构示意图

关于边棱音的发声机理至今仍然是研究者关注的焦点。Brown对空气中的低速边棱音进行了较完整的研究，提出“涡流导致边棱音”的理论，并进一步探讨边棱音的发生机理。在随后的20多年里，Curle[3]进一步研究了边棱音的流体动力学和漩涡观点。Bamberger A等人[4]对边棱音进行了实验和数值模拟，通过这两种方式来验证Brown提出的频率与喷嘴厚度以及喷嘴到边棱之间距离的关系，发现实验与模拟具有很好的一致性，并与Brown提出的观点相一致。Paal G等[5]通过模拟发现射流抖动并且在边棱两侧产生不对称涡街，并证明频率阶段的存在，这也与Brown观察到的相一致。Nyborg[6]提出的动力学理论，与其他人不同的是假设射流是一系列离散的质量粒子的波动。甚至还有人认为边棱音发声装置之所以能够发声是由于射流液片中包含各种频率成分，某些频率与边棱产生共振，从而发声。罗曾义[7]提出了位移反馈发声机理，认为簧片哨发声系统实际上是一个自激振动系统，即由射流液片的抖动激发了簧片的振动，而簧片的振动反过来影响或控制液片的摆动和激发力。Takahashi K等[8]依据空气动力学声理论对边棱音发声系统进行2维和3维的数值模拟，模拟结果表明声压的频率与射流速度成正比,特别是三维模型的模拟结果与Brown的方程几乎一致。

随着计算机的发展，模拟仿真给实验研究提供了依据，并且也节省了大量的时间和费用，本文利用有限元体积法对以液体为动力的边棱音发声系统进行了数值模拟，研究了低速时边棱音发生装置的发声机理及其特性。

1 模型和计算网格

本文模拟所采用的二维几何模型如图2所示，由一个喷嘴和正对着喷嘴放置的簧片所组成。有限元体积法的计算网格如图3所示。两种不同簧片的几何尺寸见表1。根据实际簧片，定义材料的杨氏模量为2.09e11Pa，泊松比为0.3，密度设为7860 kg/m3。簧片的劈尖角度均为30°。喷嘴出口到簧片尖端的距离(表1中简称喷距)均为10 mm，具体参数见表1。簧片的一端固定，一端自由，网格划分采用的是四边形网格，采用耦合隐式求解的计算方法。边界入口为速度入口(velocity-inlet)，其它边界设为硬边界(wall)。

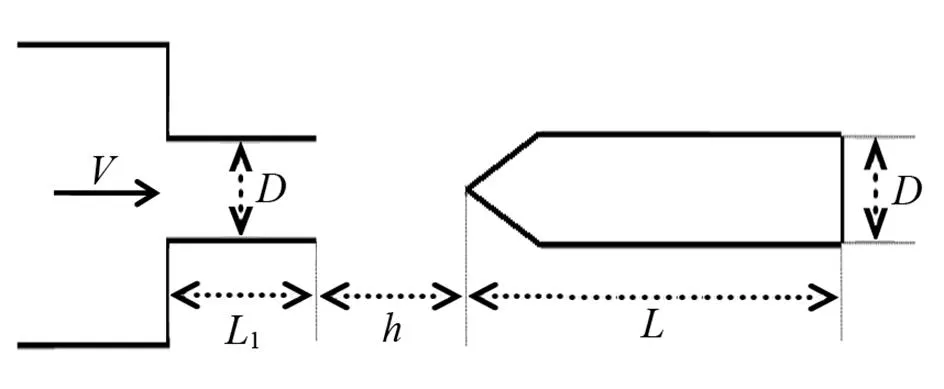
图2 二维模型

图3 计算网格

表1 喷嘴、喷距以及簧片的参数

2 数值模拟结果及分析

簧片哨实际工作在湍流状态，但是由于湍流本身的复杂性，为研究工作带来了很大的困难。为此，本文在进行研究时，为了能直观清晰地获得簧片的振动特征，选择了低于湍流的液体射流流速，并且认为射流是在不稳定的情况下工作。模拟计算中，在喷嘴的厚度、簧片的大小以及喷嘴出口到簧片尖端的距离不变的情况下，通过改变射流速度得到不同簧片尖端处以及两侧的漩涡、速度和压力分布云图，以此研究簧片两侧旋涡、压力以及速度的分布对簧片的作用；同时还研究了在同一射流速度下，不同簧片尖端处以及两侧的射流特性和压力分布特性。

2.1 射流特性

图4所示的是边棱两侧的旋涡分布情况，涡量大小由色标给出，单位为1.s-1。对应簧片的尺寸为56 mm×34 mm×1 mm，在不同流速下，簧片的两侧均能产生明显的不对称涡街，但是所产生的涡街的旋向与卡门涡街的旋转方向相反。卡门(绕流)涡街是两列向前行进、向内旋转的涡，而射流的涡街是两列向前行进、向外旋转的涡。由狭缝出口喷射出来的射流扰动簧片的劈尖，被放大的扰动交替作用在簧片两个侧面，由于簧片表面压力与附近低压区的压力差作用，使得原速度的法向指向低压力区，所以受法向力作用产生向心加速度，就形成了旋涡。因而在簧片的两侧形成反对称涡街。由旋涡组成的涡街向下游运动的过程中，先是增强，在达到极限后，最后涡街发生脱落，直至溃灭。

图5给出了簧片为47 mm×34 mm×1 mm的旋涡分布云图，模拟结果表明：改变簧片长度，在簧片的两侧均能产生交替分布的旋涡；并且对于同一个簧片，在不同的射流速度下，随着射流速度的增加旋涡在簧片两侧的分布越来越明显。而且在相同流速下，随着簧片长度的增加，簧片两侧旋涡的分布也会越来越明显。

图4 漩涡云图

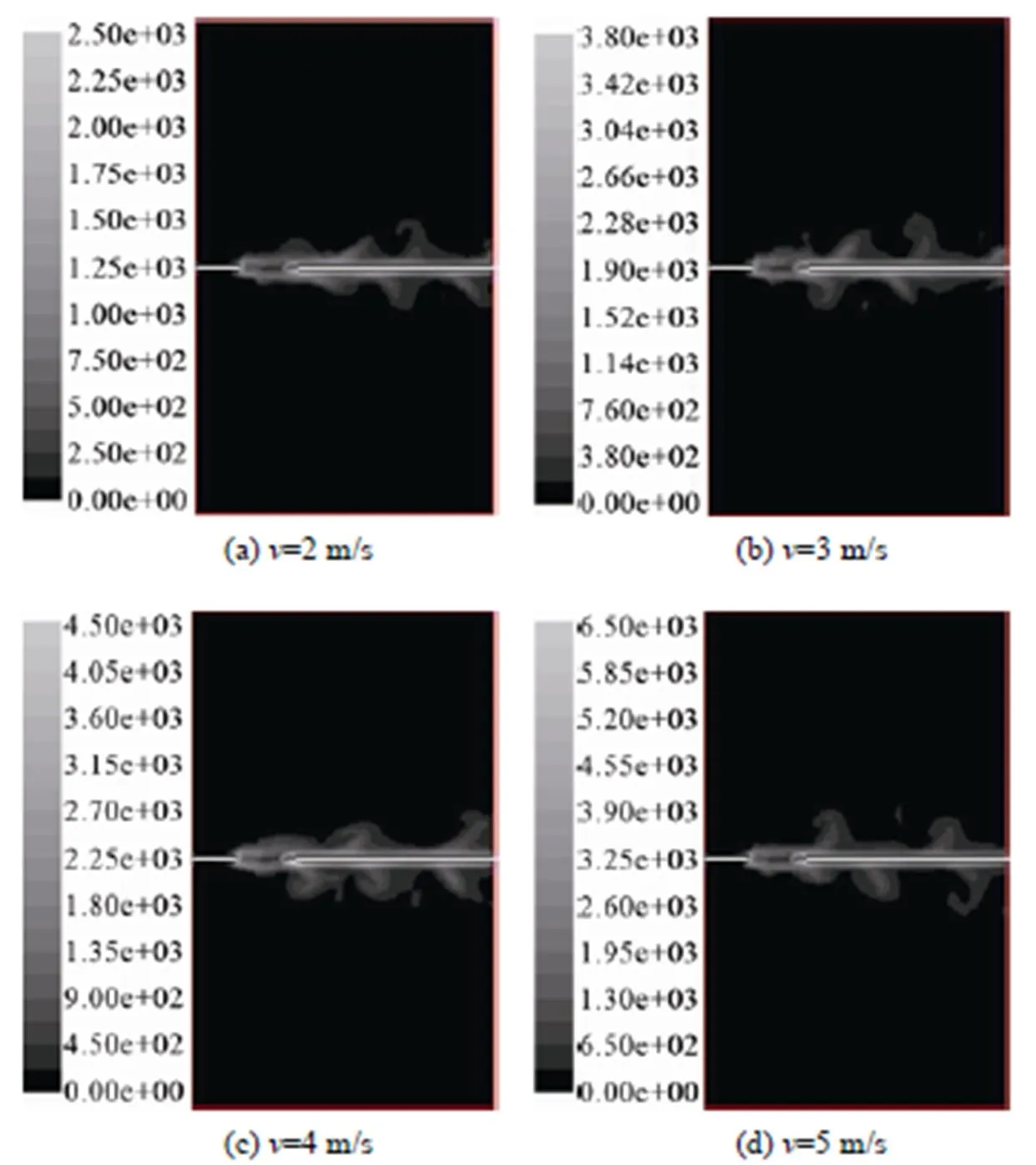
图5 漩涡分布

研究时假设射流具有不稳定特性。图6所示的簧片为56 mm×34 mm×1 mm，在几种不同流速下的射流的速度云图。图中的色标表示速度的大小，单位m/s，图7同。速度云图明显地表现出射流具有交变的抖动特性，而且在簧片的尖端处射流发生分离，在簧片的两侧交替分布，这就为旋涡的产生提供了一定的条件，形成的旋涡产生的横向作用力作用于簧片，使簧片发生振动。

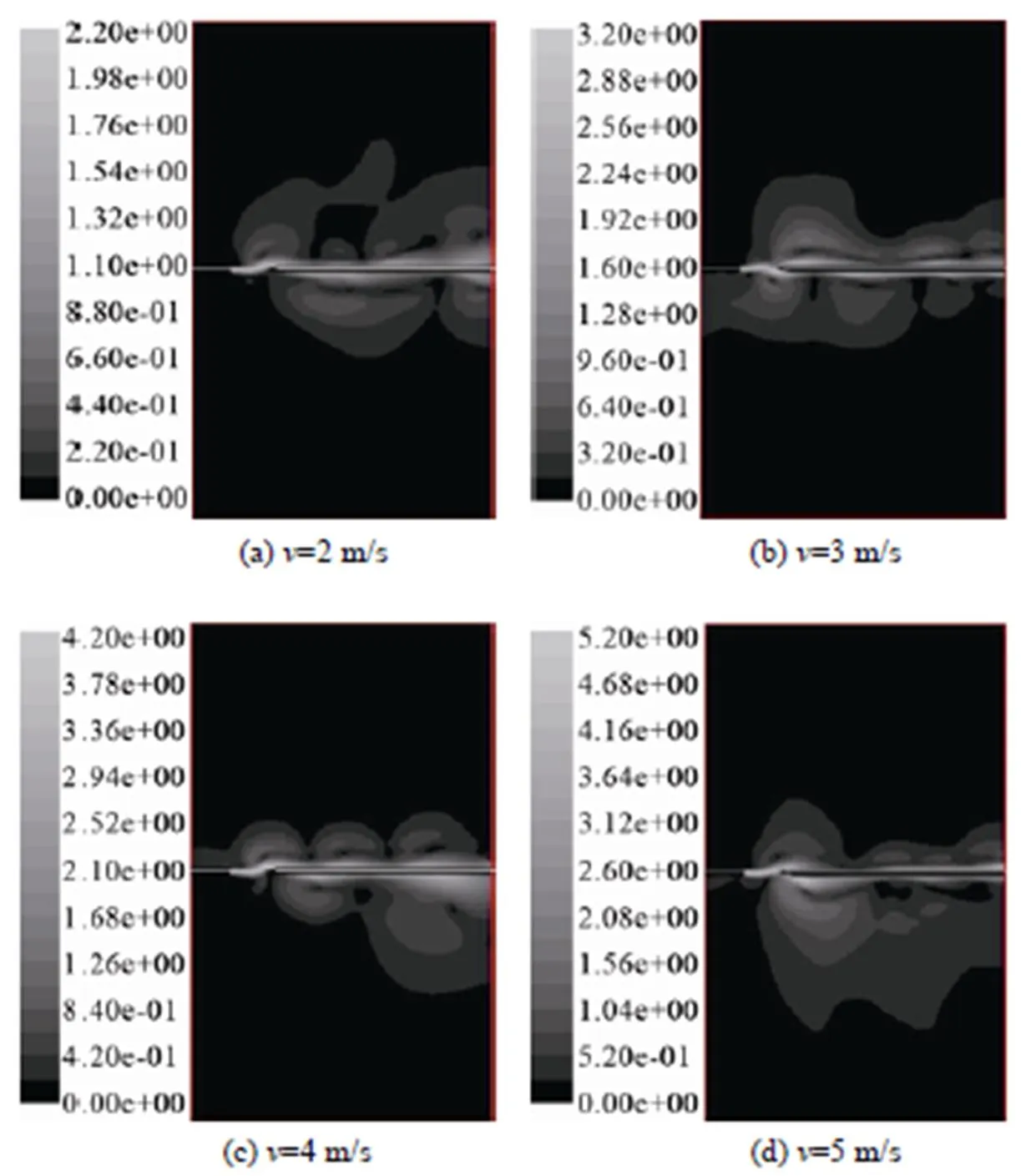
图6 速度云图

图7给出的是47 mm×34 mm×1 mm的簧片两侧的射流速度分布图，同样可以观察到射流具有抖动现象，并且随着射流速度的增加，射流的抖动增强，而且簧片的长度越长，射流的抖动现象越明显。

2.2 簧片两侧压力特性

图8所示的是不同流速下簧片尖端以及两侧的压力图，图中色标表示压力的大小，单位Pa，图9同。从图中可以看出在簧片的劈尖处压力最大，并且在簧片的两个侧面上呈现出压力极大值与极小值的交替分布。从涡街的概念来解释，就是当射流以适当的速度绕过簧片的劈尖后，在簧片两侧的涡旋形成不对称排列涡街。由于涡街的交替发放，会在簧片上产生垂直于流动方向的交变侧向力，力的作用迫使簧片自由端的劈尖产生位移，而簧片的劲度产生相反的力，使其趋向平衡位置。当下一个相反相位的抖动到来时，产生的力加大簧片位移，簧片的劲度同样产生相反的力来保持其平衡，于是簧片产生振动。当涡街的发放频率与簧片的固有频率相耦合时，就会因共振而产生较大的振幅，从而就会产生可听到的边棱音。

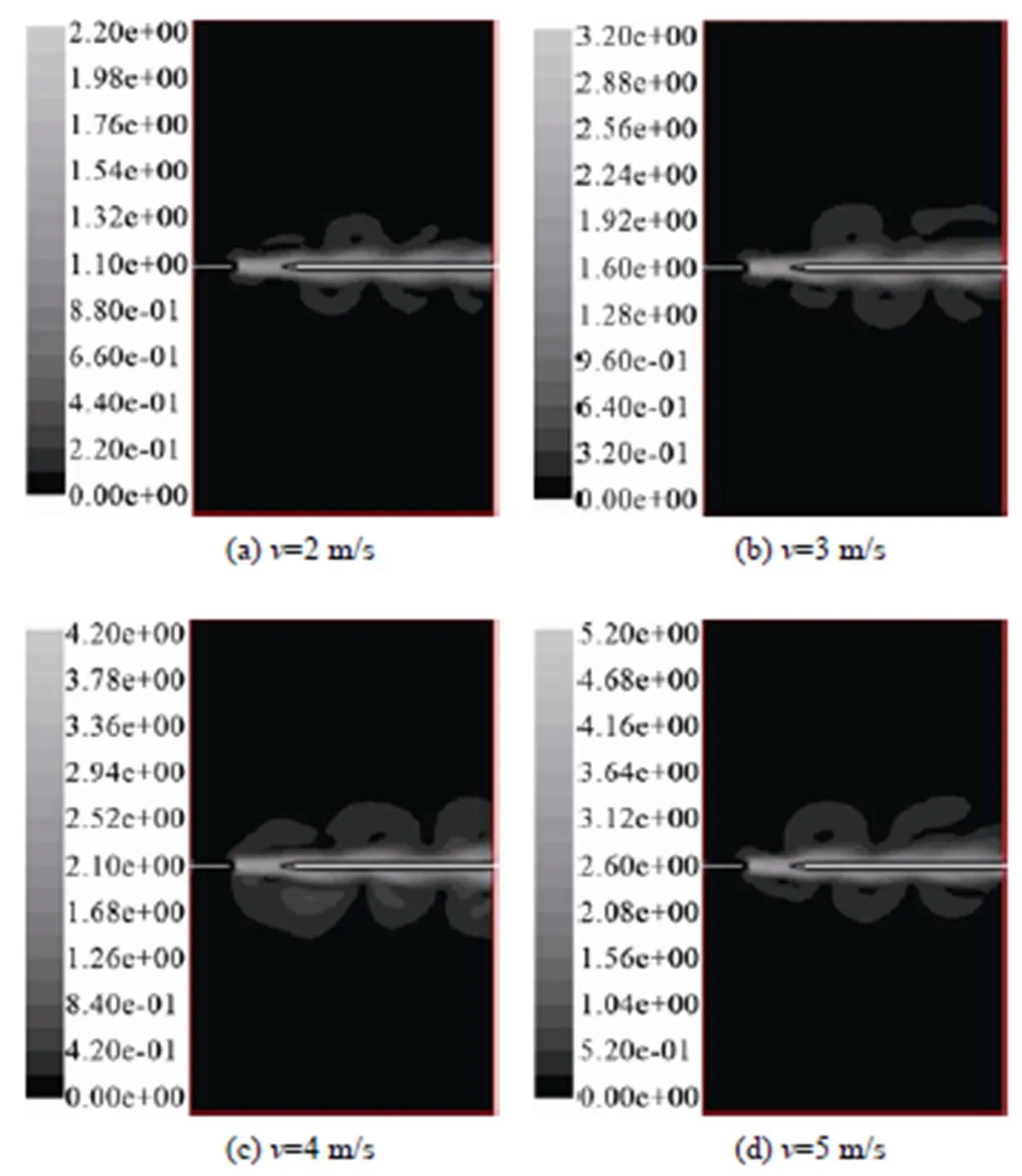
图7 速度分布

图8 压力云图

图9是47 mm×34 mm×1 mm的簧片的尖劈以及两侧的压力分布图，与图8中的压力分布一样，尖劈处压力最大，簧片两侧压力交替分布，并且随着簧片上距离的增加，压力在减小，这主要是由于旋涡的脱落，对簧片的横向作用力减小而引起的。

从图10给出的簧片压力分布可知，总压力在簧片尖劈处最大，这与图8、图9观察到的现象相一致，并且随着距离的增加压力减小，这也从另一个方面说明，非定常射流的不稳定性，以及随着旋涡向下游运动，能量的耗散。但是，在不同流速下，在同一位置处的压力随射流速度的增加而增大。

图9 压力分布

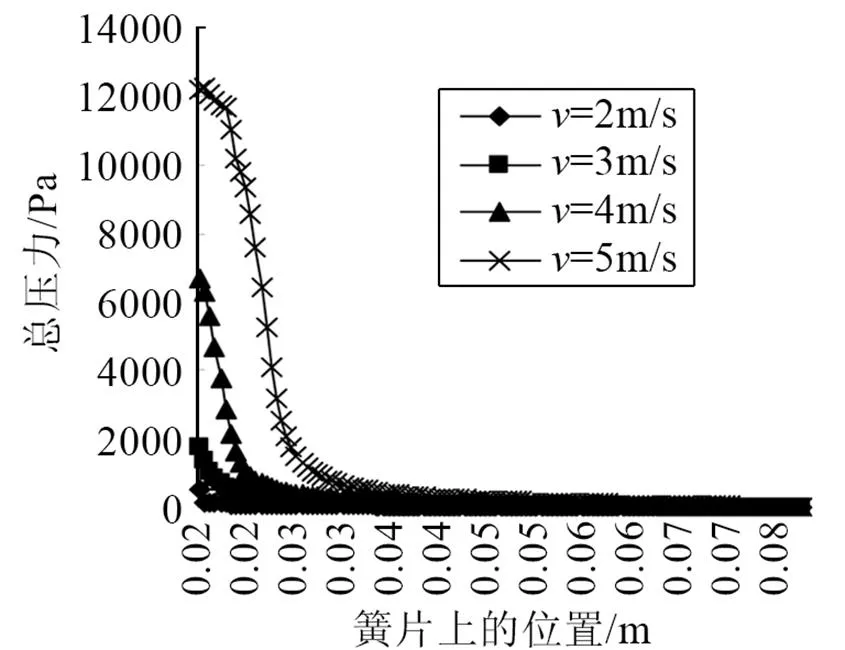
图10 簧片上总压力分布

3 结语

本文对边棱音发声系统进行了数值模拟，在其它参数不变的情况下，改变射流速度来观察簧片尖劈和边棱上的旋涡、压力以及速度分布云图；在相同射流速度下，改变簧片的长度来观察簧片两测的旋涡、速度、压力分布。模拟结果可清晰地看到射流具有抖动现象，这为旋涡的形成提供了条件，继而在边棱两侧产生交替分布的旋涡；射流速度一定时，旋涡随簧片长度的增加在簧片两侧的分布越来越明显；压力在尖劈处最大，在边棱处和旋涡一样交替分布，这与Brown在空气中观察的现象相吻合。

[1] 马大猷. 声学手册[M]. 北京: 科学出版社, 2004: 218.

MA Dayou. Acoustic manual[M].Beijing: Science Press, 1983: 200.

[2] Brown G B. The vortex motion causing edge tones[J]. Proc. Phys. Soc. London. 1937, 49 (5): 493-507.

[3] Curle N. The mechanics of edge-tones[J]. Proc. Roy. Soc. Lond. A, 1953, 216(1126): 412- 424.

[4] Bamberger A, Ansch E B, Siebert K G. Experimential and numerical investigation of edge tone[J]. Z. Angew. Math, 2004, 84(9): 632-646.

[5] Paal G, Vaik I. Unsteady phenomena in the edge tone[J]. International Journal of Heat and Fluid Flow, 2007, 28(4): 575-586.

[6] Nyborg W L. Acoustical characteristics of jet-edge and jet-edge-resonator systems[J]. J. Acoust. Soc. Am., 1952, 24(3): 293.

[7] 罗曾义, 邓文海. A6悬臂梁式簧片哨工作特性的研究[J]. 声学技术, 1996, 15(4): 166- 169.

LUO Zengyi, DENG Wenhai. The research of characteristics of A6 cantilever beam reed whistle [J].Technical Acoustics, 1996, 15(4): 166-169.

[8] Takahashi K, Miyamoto M, Ito Y, et al. Numerical analysis on 2D and 3D edge tones in terms of aerodynamic sound theory[C]// Sydney, Australia. ICA 2010, August 2010.

The vibration characteristics oflow speed edge-tone

DI Hui-fang1, WU Sheng-ju1,2, LI Feng-ming1, XU Hao1

(1.Applied Acoustic Institute, Shannxi Normal University,Xi´an 710119, Shaanxi, China;2.Key Laboratory of Ultraphonics,Xi´an710119, Shaanxi, China)

Edge-tone is a complex fluid dynamic phenomenon. The paper researches the edge-tone phenomenon by numerical simulation which is conducted under the condition of the jet instability, but below turbulence. The distributions of vortex, velocity and pressure as well as the characteristics of the reed at different fluid speeds are studied. Simulation results show that the vortex street and pressure are alternately distributed on both sides of the reeds and the fluid is obviously shaking. Based on the phenomenon, the mechanism of vibrating reeds generating edge-tone is preliminarily discussed.

vortex; edge-tone; pressure

O421+.3

A

1000-3630(2014)-03-0227-05

10.3969/j.issn1000-3630.2014.03.009

2013-07-30;

2013-10-30

国家自然科学基金资助项目(11074158)。

邸惠芳(1985－), 女, 山西朔州人, 硕士研究生, 研究方向为声学 测量。

吴胜举, E-mail: wushju@snnu.edu.cn