互联电网功率振荡辨识方法应用研究

门 锟，吴 超，涂 亮，陆 超

1)南方电网科学研究院有限责任公司，广州 510080;

2)深圳大学机电与控制学院，深圳 518060;3)清华大学电机工程与应用电子技术系，北京 100084

互联电网功率振荡辨识方法应用研究

门 锟1，吴 超2，涂 亮1，陆 超3

1)南方电网科学研究院有限责任公司，广州 510080;

2)深圳大学机电与控制学院，深圳 518060;3)清华大学电机工程与应用电子技术系，北京 100084

为应对中国大规模互联电网的功率振荡问题，讨论Prony法、自回归滑动平均法和随机子空间法的应用性.分别以两区四机系统和EPRI-36节点系统等不同规模的典型仿真系统为例，将上述方法用于明显扰动系统响应和随机扰动系统响应等典型信号的分析，提取系统振荡特征信息，比较不同方法的应用性能，研究存在外部测量干扰时方法的使用效果，得到各种辨识方法在实际电网中应用性的一般结论.

电气工程;功率振荡;互联电网;Prony法;自回归滑动平均法;随机子空间法

随着全球能源局势的日益紧张，中国电力行业正逐步推行以特高压电网为骨干的区域电网互联模式，提出建设形成全国联网的统一坚强智能电网［1-3］.电力系统互联规模的扩大，有效改善了能源利用的经济性，但也带来新的安全隐患，尤其是大电网功率振荡问题日益突出.大规模互联电网振荡复杂度和波及范围均不断扩大，严重时甚至将导致系统解列乃至全网崩溃，极大威胁电力系统的安全稳定运行［4-5］.因此，研究大规模互联电网功率振荡问题势在必行，这是构建统一坚强智能电网进程中不可或缺的重要环节.准确分析电网功率振荡特征是掌握整个系统动态特性的重要依据，据此制定有效措施，及时抑制系统振荡现象，可有效实现特高压智能电网安全稳定性水平的全面提升.

随着智能电网信息化、数字化、自动化及互动化的不断进展，涌现出一批基于量测数据分析大电网功率振荡特性的方法和手段.Prony法、自回归滑动平均法和随机子空间法是3种典型的功率振荡辨识方法.Prony法最早用于电力系统振荡模式参数分析［6］，实现了基于不同类型量测数据的振荡特性在线分析［7-8］.之后，自回归滑动平均法［9-11］引入处理电网随机扰动响应，成功提取系统振荡参数.在讨论子空间法处理人为激励系统响应［12］的基础上，随机子空间法准确实现了系统振荡特性识别［13］.以人为激励系统响应为例，文献［14］进一步对比分析特征系统实现算法、Steiglitz-McBride法和Prony法在系统振荡辨识方面的表现.文献［15］比较了Yule Walker法、Yule Walker with Spectral法和子空间法在系统振荡特性估计上的性能.文献［16］则对Prony法和自回归滑动平均法的适用性问题进行初步探讨.文献［17］对比Prony法和希尔伯特-黄变换 (Hilbert-Huang transform，HHT)方法的低频振荡参数提取效果.但在辨识方法应用分析的全面性上，现阶段研究仍存在一定的局限性，尚无文献涉及Prony法、自回归滑动平均法和随机子空间法这三种典型方法的应用性能讨论.同时，现有工作多仅针对某种特定信号进行，较少考虑各种方法在处理实际电网不同类型数据时的效果比较.这些问题都将直接影响电网调度部门能否合理针对系统不同运行工况，选用适当方法，实现互联电网功率振荡特性的准确辨识.

本研究在中国大规模互联电网背景下，从应用角度出发，对基于量测数据的Prony法、自回归滑动平均法和随机子空间法的功率振荡辨识性能进行全面比较分析.在介绍方法原理基础上，分别以两区四机系统和EPRI-36节点仿真系统为例，同时考虑实际电网所存在的外部测量干扰等问题，系统地比较各种方法基于不同类型信号的辨识效果，尝试给出其应用于功率振荡识别的一般性结论，从而为电网调度部门及时准确掌握大规模互联电网功率振荡特性提供技术支持.

1 电网功率振荡辨识方法原理

1.1 Prony法

Prony法基本思路认为，分析用信号可由一组具有任意振幅、初相位、频率和衰减因子的指数函数的线性组合来拟合，如［18］

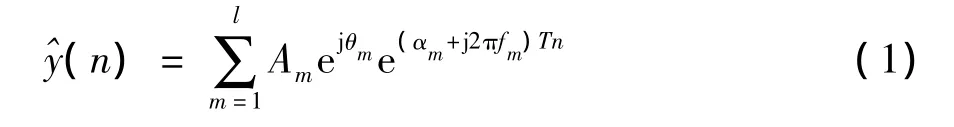
Prony法采用误差平方和最小为模型参数估计原则.具体来说，构造如式(2)的扩展阶样本函数矩阵R，确定矩阵有效秩l.

其中，εl为趋于0的极小值.在此基础上，定义式(4)所示特征多项式方程，计算得到特征根zi.根据式(5)估算电网功率振荡模式频率fi和阻尼比ξi.

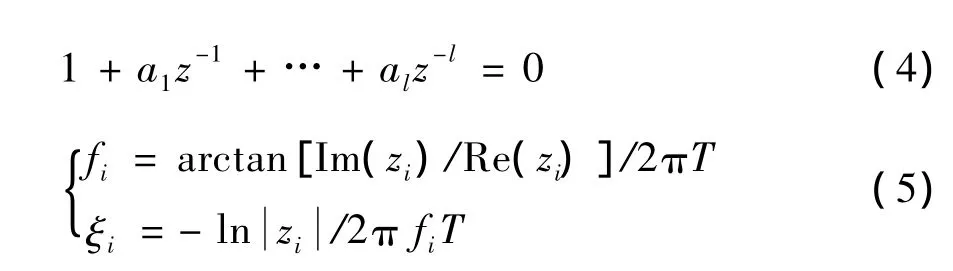
1.2 自回归滑动平均法

近年来，时间序列模型思想被逐步引入电网功率振荡特征分析中.自回归滑动平均模型［19］是最常用的时序模型之一，在线性回归模型的基础上引申并发展起来，其结构为

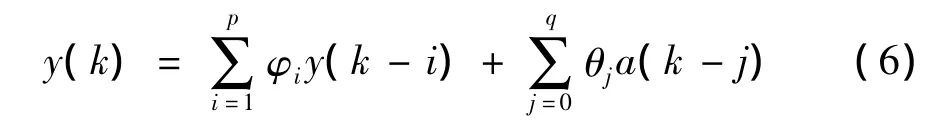
其中，y(k)为分析用信号;p和q分别为自回归部分和滑动平均部分模型阶数;φi和θj分别为自回归部分和滑动平均部分模型参数;a为输入信号.

根据自协方差函数定义，可推得

其中，Rl为信号自协方差函数.当j＞q时，存在

在此基础上，根据式(9)构造矩阵方程，计算得到自回归部分模型参数.

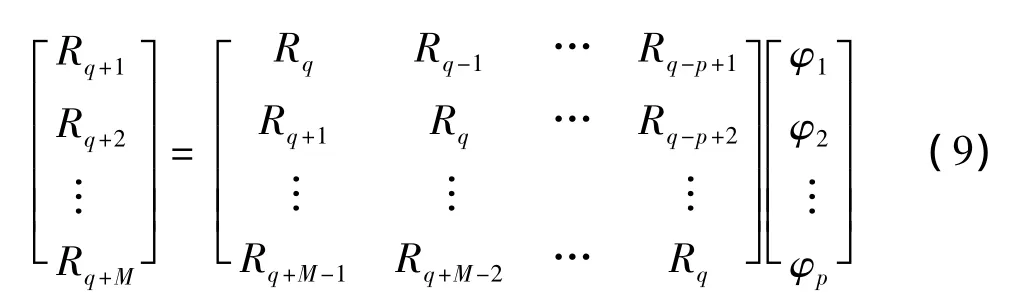
求解自回归部分多项式方程特征根zi，并根据式(10)估计电网功率振荡模式频率 fi和阻尼比ξi.

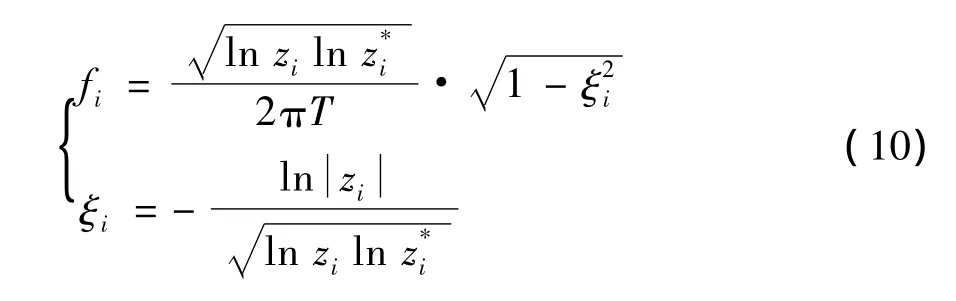
1.3 随机子空间法

随机子空间法［20-21］的核心思想是把“将来”的输出行空间投影到“过去”的输出行空间，利用系统输出数据构造Hankel矩阵，分离得到系统状态矩阵，最终实现系统的振荡参数识别.

具体来说，随机子空间法以线性离散状态空间方程为基础，

其中，yk∈Rl×l为第l个测点在第k个采样时刻的输出向量;xk∈Rn×l为系统在该采样时刻的状态向量;wk∈ Rn×l和 vk∈ Rl×l分别为过程噪声和测量噪声;A∈Rn×n表示状态矩阵;C∈Rl×n为输出矩阵.

首先构造Hankel矩阵，并进行LQ分解，为

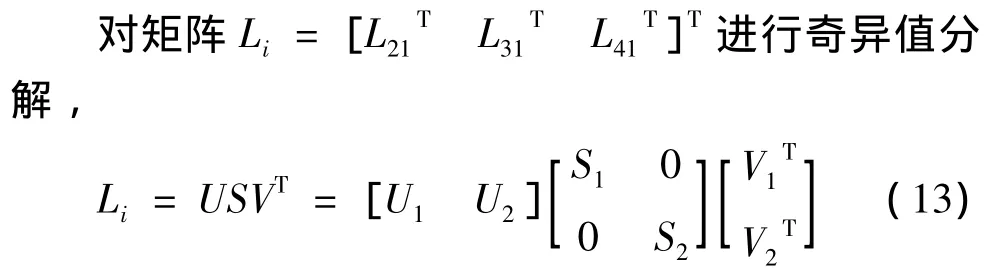
其中，U和V是正交矩阵;S1∈Rn×n是奇异值组成的对角矩阵，且奇异值沿对角线降序排列，n＜ri;S2是噪声导致的虚假模态对应的奇异值.

根据式(14)计得系统矩阵A和输出矩阵C为

其中，［·］+表示求广义逆;是可观测矩阵，Oi-l由Oi去掉l行得到.

在此基础上，求解矩阵A对应特征值zi，并根据式(10)实现电网功率振荡特性参数识别.

2 两区四机系统仿真分析

为全面讨论Prony法、自回归滑动平均法和随机子空间法在互联电网功率振荡辨识方面的应用性能，首先以两区四机系统为例，模拟实际电网的典型运行情况，采用3种方法处理不同类型典型信号，系统比较各种方法的振荡特征分析效果.

两区四机系统如图1，系统参数详见文献［4］.

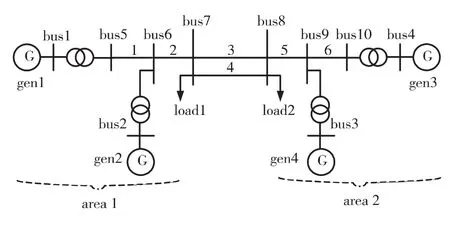
图1 两区四机系统Fig.1 Two-area four-machine system

2.1 仿真系统运行设置

观察广域测量信号可知，大电网实测信号可划分为明显扰动系统响应和随机扰动系统响应两大类［16］.其中，明显扰动系统响应是由系统内某种短时明显扰动所引起，随机扰动系统响应则是由系统日常正常运行过程中持续存在的负荷投切与变化等随机性质小幅扰动引起.因此，在仿真系统中设置不同运行情况，模拟生成上述典型信号，如表1.

表1 仿真系统运行条件设置Table 1 Simulation system operating condition setting

2.2 明显扰动系统响应

以短路故障后联络线有功功率信号为分析对象，分别采用Prony法、自回归滑动平均法和随机子空间法处理提取系统特征参数.采用滑动数据窗思路以改善分析的准确性，数据窗时长5 s，时间间隔2 s，综合平均共计10个数据窗的分析结果，计得系统振荡特性参数，如表2.

由表2可见，与仿真系统小干扰稳定计算结果比较，基于短路故障后联络线有功功率信号，3种方法对振荡模式频率的辨识误差基本控制在3%左右，对振荡模式阻尼比的辨识误差基本低于11%，分析准确度均较为理想.

表2 基于明显扰动系统响应的辨识结果Table 2 Results based on ringdown data

由此可知，以明显扰动系统响应为分析对象，Prony法、自回归滑动平均法和随机子空间法均可实现电网功率振荡特征的基本准确识别，其中，模式频率辨识准确度略高，3种方法均基本符合工程应用要求.

2.3 随机扰动系统响应

以仿真系统各负荷注入随机小幅扰动时的联络线有功功率信号为分析对象，分别使用Prony法、自回归滑动平均法和随机子空间法计算系统振荡参数.

在实际电网中，这种随机扰动系统响应是因负荷小幅扰动所引起，导致信号中所包含的系统动态特性信息相对有限，因此提出以长数据窗信号为分析对象，数据窗时长1 min，时间间隔10 s.前期试验发现，Prony方法对于长数据窗信号的拟合效果不够理想.为改善分析的准确性，在使用Prony法时，改用时长10 s的数据窗信号进行分析，数据窗时间间隔3 s.在此基础上，对共计10个数据窗的分析结果进行综合平均，计算得到系统振荡模式参数，如表3.

由表3可见，基于负荷随机小扰动时联络线有功功率信号，Prony法对于振荡频率的辨识准确性明显优于阻尼比的辨识准确性，前者误差3%左右，后者误差则高达70%;而自回归滑动平均法和随机子空间法对振荡频率和阻尼比等参数辨识误差基本控制在3%和15%之内.

由此可知，以随机扰动系统响应为分析对象，与Prony法相比，自回归滑动平均法和随机子空间法的电网功率振荡辨识效果明显更佳，其中模式频率准确度略高，均基本符合工程应用要求.

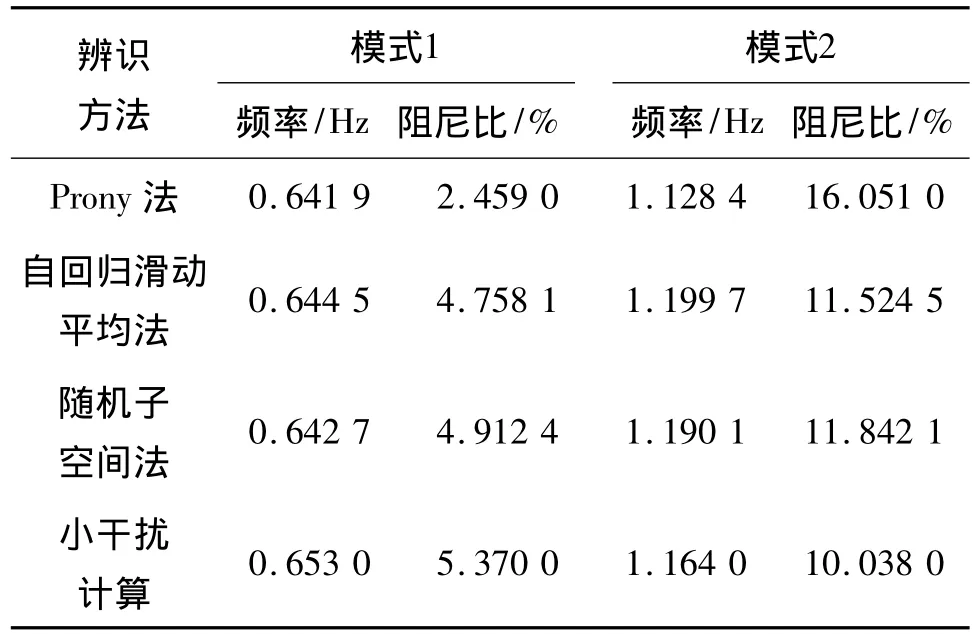
表3 基于随机扰动系统响应的辨识结果Table 3 Results based on ambient data

2.4 辨识方法应用比较结果

基于两区四机系统仿真分析结果可知，3种辨识方法在电网功率振荡辨识方面的应用性有所区别.Prony法仅适合于从明显扰动系统响应中提取振荡信息，而自回归滑动平均法和随机子空间法则同时适合基于明显扰动系统响应和随机扰动系统响应的电网功率振荡特征分析，后两种方法的应用性更为理想.

3 EPRI-36节点系统仿真分析

通过进一步观察电力系统广域测量信号可知，在实际电网中明显扰动的发生概率相对较小，数据量有限，安排专门试验也存在较大困难，难以及时准确反映系统当前动态特性，这种方式只能实现扰动后的系统告警，而无法实现预警.另一方面，实际电网中负荷投切与变化等随机性质小幅扰动始终存在，所引起的类似噪声的随机扰动系统响应更易于采集，可以在电网日常正常运行过程中即实现对系统特性的准确掌握，有助电网调度运行部门针对性制定预防控制措施，实现对特高压智能电网安全稳定运行水平的全面提高.

因此，为深入讨论自回归滑动平均法和随机子空间法在实际大规模互联电网中的应用问题，以结构更为复杂的典型EPRI-36节点仿真系统 (如图2)为例，重点对这两种方法应用于处理随机扰动系统响应时的辨识情况进行探讨，仿真系统参数详见文献［22］.

图2 EPRI-36节点仿真系统Fig.2 EPRI-36-node benchmark system

为模拟实际电力系统中的小幅随机扰动，在36节点仿真系统各个负荷处注入随机性质小幅扰动功率信号，采集母线19与21联络线有功功率信号为分析对象，信号时长5 min.

3.1 随机扰动系统响应

分别采用自回归滑动平均法和随机子空间法从随机扰动系统响应中提取系统振荡特性参数.滑动数据窗时长1 min，数据窗间隔10 s.两种方法辨识结果与小干扰稳定计算特征值结果之间的误差如图3.其中，实线表示自回归滑动平均方法分析结果;虚线表示随机子空间法分析结果;横坐标表示参与平均的数据窗个数;纵坐标为各参数辨识结果误差;ef1和 ef2表示两个模式频率辨识误差;eξ1和 eξ2表示两个模式阻尼比辨识误差.

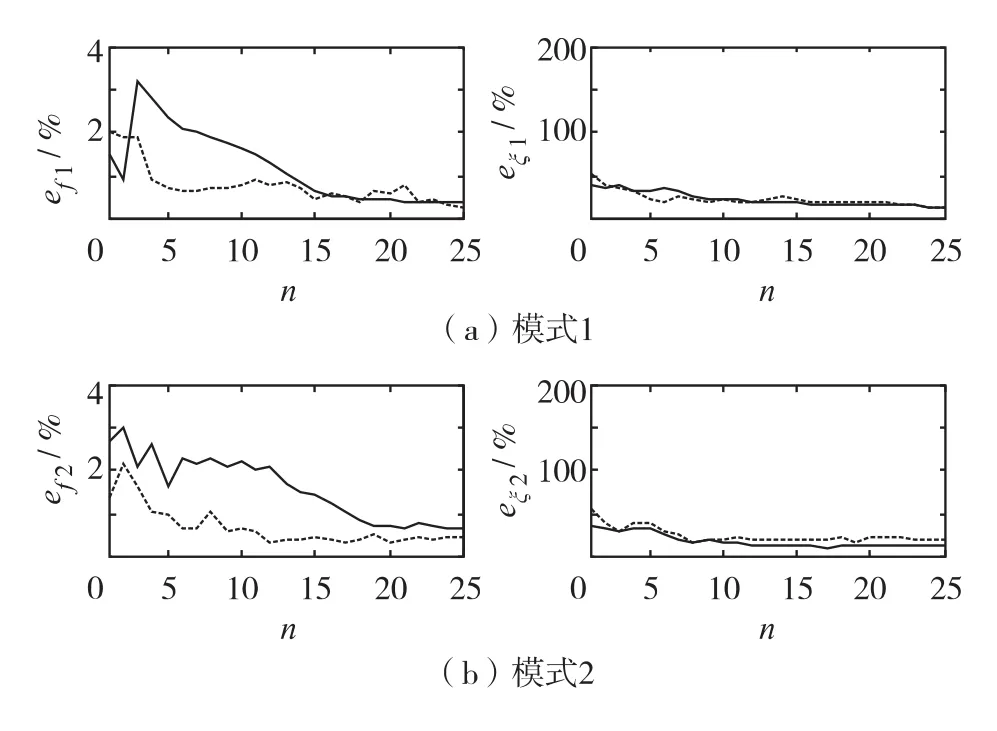
图3 两种辨识方法分析结果Fig.3 Results of two approaches

观察发现，采用自回归滑动平均法处理随机扰动系统响应时，两个模式频率辨识误差波动分别为0.4% ～3.2%和 0.6% ～3.0%，两个模式阻尼比辨识误差波动分别为15%～40%和12%～35%，随着分析用信号时长的增加，上述参数误差分别接近0.4%、0.6%、15.0%和14.0%;采用随机子空间法处理随机扰动系统响应时，模式1频率和阻尼比辨识误差分别为0.3% ～2.0%和15% ～50%，模式2频率和阻尼比辨识误差分别为0.32% ～2.50%和18%～55%，增加信号时长，上述误差分别趋于0.3%、0.5%、15%和20%.由此再次证明，自回归滑动平均法和随机子空间法均可基本准确地从随机扰动系统响应中提取系统振荡特征信息，对模式频率的分析准确性略高.

3.2 外部干扰影响分析

考虑到实际电网中不可避免地存在诸如测量误差等外部未知干扰，而因负荷小幅随机扰动引起的系统响应所包含的动态特性信息又相对有限，导致外部干扰必然会影响辨识方法对系统特性的分析效果.因此，提出在仿真信号中加入一定能量的随机噪声以模拟外部干扰情况，更深入地对自回归滑动平均法和随机子空间法的应用问题进行研究.

以母线19与21联络线有功功率信号为辨识对象，加入不同能量大小的随机性质扰动，分别构造信噪比指标为40、30和20 dB的信号用于分析.为全面探讨辨识方法的应用情况，采用Monte Carlo思路，进行50次仿真计算，振荡模式对应特征值计算结果如图4.其中，左图表示自回归滑动平均法结果，右图表示随机子空间法结果，‘+’表示50次仿真特征值辨识结果，‘o’表示小干扰稳定计算特征值计算结果.

显然，当分析信号信噪比高于20 dB时，自回归滑动平均法和随机子空间方法估计的系统特征值分布情况较为类似，相比模式1特征值的集中分布，模式2特征值分布较为分散，同时两个模式特征值实部变化范围均相对较大.随着辨识信号信噪比指标的逐步降低，两个模式特征值分布愈加松散.当信噪比降至20 dB时，与随机子空间法相比，自回归滑动平均法对模式2的辨识结果明显偏离小干扰稳定计算结果.

图4 加入外部干扰后随机扰动系统响应辨识结果Fig.4 (Color online)Results based on ambient signal with disturbances

由此可知，当外部干扰能量较小时，两种方法均可以基本准确地从随机扰动系统响应中提取系统振荡特性，而对模式频率的分析准确度略高.当外部干扰能量较大，分析用信号信噪比低于20 dB时，自回归滑动平均法辨识效果明显恶化，而随机子空间法仍具有较好的辨识效果，即后者在实际大电网中的应用效果将更为理想.

3.3 辨识用信号数量影响分析

进一步讨论辨识用信号数量对两种辨识方法应用性的影响.分别采用2信号、3信号和5信号等不同信号组合进行计算，如表4.分析结果如图5.图5左边分图为自回归滑动平均法结果，右边分图为随机子空间法结果，‘+’表示50次仿真特征值辨识结果，‘o’表示小干扰稳定计算特征值计算结果.

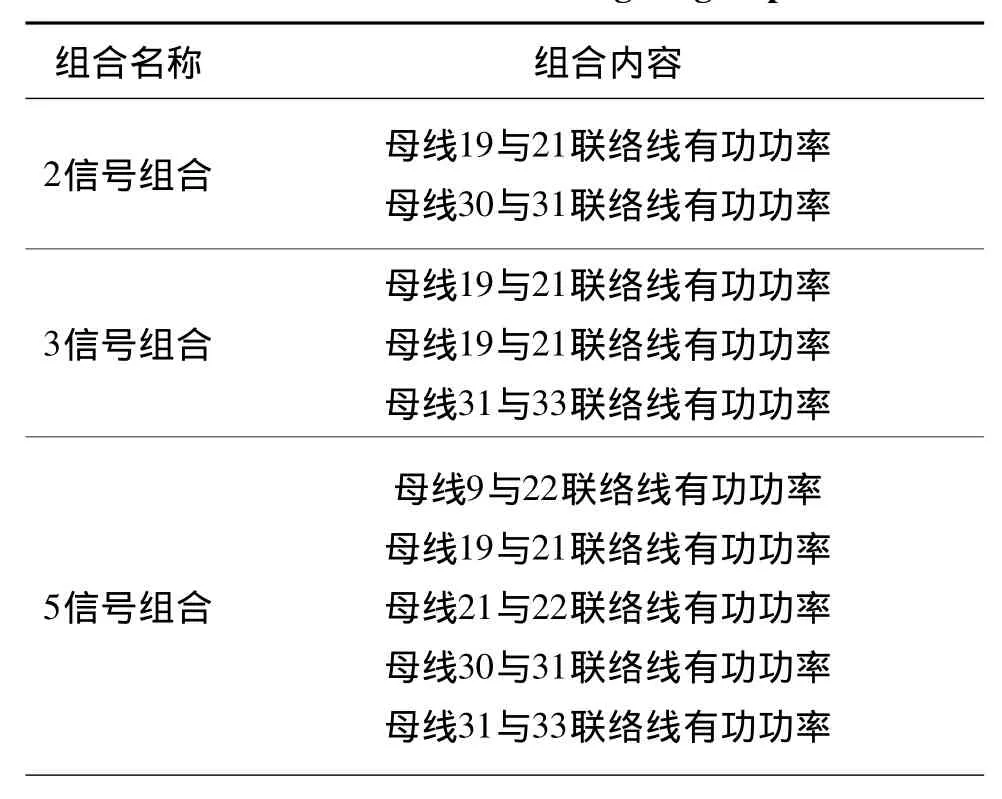
表4 辨识用信号组合Table 4 Identification signal groups

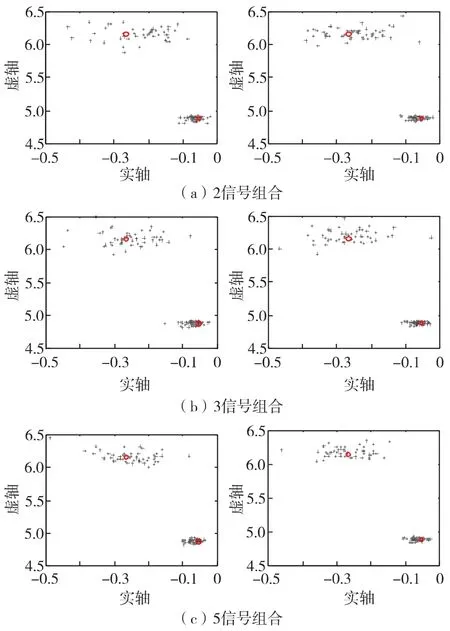
图5 不同信号组合辨识结果Fig.5 (Color online)Results of different signal groups

由图5可见，随着随机扰动系统响应信号数量的增多，两种辨识方法结果中两个模式特征值分布均逐步集中化.这是因为，随着信号数量增加，系统动态特性信息随之增多，辨识效果相应改善.由此证明，适当增加辨识用信号的数量，可以有效改善系统振荡辨识的准确性，进一步提高辨识方法的应用性.

结 语

为应对我国大规模互联电网功率振荡问题，以不同规模典型仿真系统和不同类型典型信号为分析对象，系统比较了Prony法、自回归滑动平均法和随机子空间法三种典型功率振荡辨识方法的性能，研究认为，Prony法仅适合基于明显扰动系统响应的振荡分析;自回归滑动平均法和随机子空间法均可从明显扰动系统响应和随机扰动系统响应中，基本准确地识别系统振荡参数;随机扰动系统响应中外部干扰能量增加，将可能导致自回归滑动平均法辨识效果恶化;而适当增加辨识信号数量，可一定程度改善方法分析的准确性;在这3种方法中，随机子空间法在电网功率振荡辨识方面的应用性最佳.

/References:

［1］Yu Yixin，Luan Wenpeng.Smart grid［J］.Power System and Clean Energy，2009，25(1):7-11.(in Chinese)

余贻鑫，栾文鹏.智能电网 ［J］.电网与清洁能源，2009，25(1):7-11.

［2］Xiao Shijie.Consideration of technology for constructing Chinese smart grid ［J］.Automation of Electric Power Systems，2009，33(9):1-4.(in Chinese)

肖世杰.构建中国智能电网技术思考 ［J］.电力系统自动化，2009，33(9):1-4.

［3］Zhou Xiaoxin，Chen Shuyong，Lu Zongxiang.Review and prospectforpowersystem developmentand related technologies:a concept of three-generation power systems［J］.Proceedings of the CSEE，2013，33(22):1-11.(in Chinese)

周孝信，陈树勇，鲁宗相.电网和电网技术发展的回顾与展望——试论三代电网 ［J］.中国电机工程学报，2013，33(22):1-11.

［4］Kunder P.Power system stability and control［M］.New York(USA):McGraw-Hill Incorporated，1994.

［5］Ni Yixin，Chen Shousun，Zhang Baolin.Dynamic power system theory and analysis［M］.Beijing:Tsinghua University Press，2002.(in Chinese)

倪以信，陈寿孙，张宝霖.动态电力系统的理论和分析［M］.北京:清华大学出版社，2002.

［6］Hauer J F，Demeure C J，Scharf L L.Initial results in prony analysis of power response signals［J］.IEEE Transactions on Power Systems，1990，5(1):80-89.

［7］Xiao Jingyu，Xie Xiaorong，Hu Zhixiang，et al.Improved Prony method for online identification of low-frequency oscillations in power systems［J］.Journal of Tsinghua University Science and Technology，2004，44(7):883-887.(in Chinese)

肖晋宇，谢小荣，胡志祥，等.电力系统低频振荡在线辨识的改进Prony算法［J］.清华大学学报自然科学版，2004，44(7):883-887.

［8］Wu Chao，Cao Guangzhong.Low frequency oscillation ambient signals identification based on random decrement technique and Prony method［J］.Automation of Electric Power Systems，2013，37(8):53-58.(in Chinese)

吴 超，曹广忠.基于随机减量技术和Prony方法的低频振荡类噪声辨识 ［J］.电力系统自动化，2013，37(8):53-58.

［9］Pierre J W，Trudnowski D J，Donnelly M K.Initial results in electromechanical mode identification from ambient data［J］.IEEE Transactions on Power Systems，2001，12(3):1245-1251.

［10］Wies R W，Pierre J W，Trundnowski D J.Use of ARMA block processing for estimating stationary low-frequency electromechanical modes of power systems［J］.IEEE Transactions on Power Systems，2003，18(1):167-173.

［11］Wu Chao，Lu Chao，Wang Tian，et al.Ambient signals based power system oscillation modes identification considering model order selection［C］//Proceedings of Power＆ Energy Society General Meeting.Calgary(Canada):IEEE Press，2009:1-7.

［12］Kamwa I，Trudel G，Gerin-Lajoie L.Low-order black-box models for control system design in large power systems［J］.IEEE Transactions on Power Systems，1996，11(1):303-311.

［13］ Ni Jingmin，Shen Chen，Liu Feng.Estimation of the electromechanical characteristics of power systems based on a revised stochastic subspace method and the stabilization diagram ［J］. Scientia Sinica(Technologica)，2012，42(6):687-696.(in Chinese)

倪敬敏，沈 沉，刘 锋.基于改进随机子空间法和稳定图技术的电力系统低频机电振荡特征识别 ［J］.中国科学:技术科学，2012，42(6):687-696.

［14］Sanchez-Gasca J J，Chow J H.Performance comparison of three identification methods for the analysis of electromechanical oscillations［J］.IEEE Transactions on Power Systems，1999，14(3):995-1001.

［15］Trudnowski D，Pierre J W，Zhou N，et al.Performance of three mode-meter block-processing algorithms for automated dynamic stability assessment［J］.IEEE Transactions on Power Systems，2008，23(2):680-690.

［16］Wu Chao，Lu Chao，Han Yingduo，et al.Comparison of applicability in low frequency oscillation mode identification between Prony and ARMA ［J］.Electric Power Automation Equipment，2010，30(3):30-34.(in Chinese)

吴 超，陆 超，韩英铎，等.Prony方法和ARMA法在低频振荡模式辨识中的适用性比较 ［J］.电力自动化设备，2010，30(3):30-34.

［17］Li Chengxin，Liu Junyong，Wang Ying.Comparative study of Prony and HHT applicability in low frequency oscillation parameter extraction ［J］.East China Electric Power，2012，40(10):1719-1723.(in Chinese)

李成鑫，刘俊勇，汪 颖.Prony和HHT在低频振荡参数提取中的比较研究 ［J］.华东电力，2012，40(10):1719-1723.

［18］Scharf L.Statistical signal processing:detection，estimation，and time series analysis［M］.New York(USA):Addison-Wesley Publishing Company，1991.

［19］Box G E P，M.Jenkins G，Reinsel G C.Time series-forecasting and controls［M］.Hoboken(USA):John Wiley Press，2008.

［20］Tohru Katayama.Subspace methods for system identification［M］.Hoboken(USA):John Wiley Press，2008.

［21］P van Overschee，B De Moor.Subspace identification for linearsystems:theory， implementation， applications［M］.Dordrecht(Netherlands):Kluwer Academic Publishers，1996.

［22］Wu Zhongxi，Zhou Xiaoxin.Power system analysis software package(PSASP)-an integrated power system analysis tool［C］//Proceedings of Power System Technology.Beijing:IEEE Press，1998(1):7-11.

2014-01-22;

2014-04-10

Applicability analysis of algorithms for electromechanical mode identification based on measured data

Men Kun1，Wu Chao2†，Tu Liang1，and Lu Chao3

1)Electric Power Research Institute of China South Power Grid，Guangzhou 510080，P.R.China
2)College of Mechatronics and Control Engineering，Shenzhen University，Shenzhen 518060，P.R.China
3)Department of Electrical Engineering，Tsinghua University，Beijing 100084，P.R.China

In response to the power oscillation issue of China's interconnected power grids，the applicability of the Prony method，the autoregressive moving average method and the stochastic subspace method are systematically discussed in this paper.Based on the review of their elementary principles，with the two-area four-machine system and the 36-node benchmark system as examples，these methods are used to estimate the oscillation information from ringdown data and ambient data respectively.Moreover，the influence of external measurement disturbances is also considered.Finally some general conclusions about the applicability of these methods in actual power grids are drawn from the simulation cases.

electrical engineering;power oscillation;interconnected power grid;Prony method;autoregressive moving average method;stochastic subspace method

TM 711

A

10.3724/SP.J.1249.2014.03299

Foundation:National High Technology Research and Development Program of China(2012AA050209)

†

Associate professor Wu Chao.E-mail:wuchao@szu.edu.cn

:Men Kun，Wu Chao，Tu Liang，et al.Applicability analysis of algorithms for electromechanical mode identification based on measured data ［J］.Journal of Shenzhen University Science and Engineering，2014，31(3):299-306.(in Chinese)

国家高技术研究发展计划资助项目 (2012AA050209)

门 锟 (1975—)，男 (汉族)，陕西省西安市人，南方电网科学研究院有限责任公司高级工程师、博士.E-mail:menkun@csg.cn

引 文:门 锟，吴 超，涂 亮，等.互联电网功率振荡辨识方法应用研究 ［J］.深圳大学学报理工版，2014，31(3):299-306.

【中文责编:方 圆;英文责编:海 潮】