随机和非随机部件组成的串并联系统寿命比较

李松臣，李育鹏，陈迎运，魏正红

深圳大学数学与计算科学学院，深圳 518060

随机和非随机部件组成的串并联系统寿命比较

李松臣，李育鹏，陈迎运，魏正红

深圳大学数学与计算科学学院，深圳 518060

针对随机数N个部件和非随机数n个部件组成的串并联系统，引入可交换Copula函数度量串并联系统中各部件寿命的相依性，研究串并联系统寿命的随机比较问题.利用离散函数的凸性及詹森不等式的概率论形式，证明当随机数N的期望满足条件E(N)≤n时，随机N部件组成串联系统的寿命以一般随机序优于非随机n部件组成串联系统的寿命;而当E(N)≤n时，非随机n部件组成并联系统的寿命以一般随机序优于随机N部件组成并联系统的寿命.

应用统计数学;可靠性理论;次序统计量;可交换Copula函数;串并联;一般随机序;詹森不等式;离散凸性

系统寿命的随机比较理论已广泛用于可靠性理论和系统安全领域，在系统的可靠性理论中，次序统计量发挥着关键作用.考虑最简单的串并联系统结构，串联系统是指当系统所有部件都正常工作时才能正常工作的系统，即串联系统寿命的生存函数对应串联系统各部件寿命最小次序统计量的生存函数;而并联系统仅需任意一个部件正常工作即可，其寿命的分布函数对应并联系统各部件寿命最大次序统计量的分布函数.因此，研究串并联系统的寿命等价于对部件的最小最大次序统计量进行研究.

设一个系统由非随机数(给定正整数)n个部件组成，且每个部件的寿命由非负随机变量Xi(i=1，2，…，n)表示，由此可定义这n个随机变量X1，X2，…，Xn的最小和最大次序统计量分别为 X1:n=min(X1，X2，…，Xn)和 Xn:n=max(X1，X2，…，Xn).文献［1-4］给出当样本容量为随机数N时，一组随机变量 X1，X2，…，XN的最大次序统计量 XN:N=max(X1，X2，…，XN)和 最 小 次 序 统 计 量 X1:N=min(X1，X2，…，XN)的定义、分布函数及性质;文献［5］研究样本为随机数N，且与随机变量Xi独立时，最小最大次序统计量的随机比较结果;文献［6］研究随机样本最小最大次序统计量寿命分布的随机比较结果;文献［7］证明当两个随机样本的容量N1和N2满足不同随机序关系时，对应X1:N和XN:N也有不同的随机大小关系.然而，对于随机数N和非随机数n组成的串联 (并联)系统的寿命X1:N和X1:n(XN:N和Xn:n)的随机比较及随机序关系并没引起注意.本课题组在前期研究了部件寿命独立同分布的假设下，X1:N和X1:n(XN:N和Xn:n)的一般随机序比较关系［8］.但在实际中，一方面部件的寿命随机变量独立很难满足，部件寿命存在相互依赖的情形更符合实际;另一方面，若用寿命随机变量的联合分布函数刻画系统的寿命和可靠度，则无法细致表现相依部件的寿命与整个系统寿命之间的关系，有必要引入联接函数Copula来刻画各个部件寿命的边缘分布函数与联合分布之间的关系.

本文在引入联接函数Copula基础上，研究部件寿命相依且同分布情形下，随机数N个部件和非随机数n个部件组成的串联和并联系统的寿命随机比较.介绍Copula函数及可交换Copula函数的定义、离散函数凸性和一般随机序的定义;给出串联系统中，随机数N个部件和非随机数n个部件组成串联系统的寿命X1:N和X1:n的随机比较结论;对于并联系统，有相应的结论在第3部分给出，并举例给出了研究结果的实际应用.

1 预备知识

定义1［9］称随机变量X以一般随机序小于Y(即X≤stY)，只要对任意实数 t，满足(t)≤FY(t)或FX(t)≥FY(t).

定义2［9］n元 Copula函数是一个定义域为In(其中 I= ［0，1］)的函数 C:In→ I，即

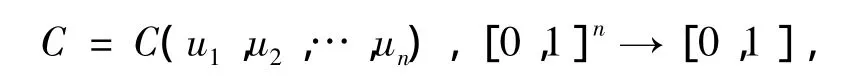
且函数C有n个［0，1］上的均匀边缘分布，另外需满足下列条件

1)对任意 ui∈［0，1］，i=1，2，…，n，有

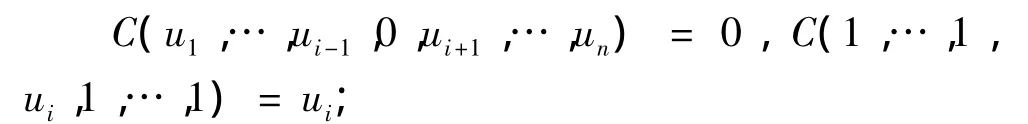
2)C(u)=C(u1，…，un)为n元增函数，即对任意 i=1，2…，n，0 ≤ai≤bi≤1，记 a=(a1，a2，…，an)T和 b=(b1，b2，…，bn)T，有

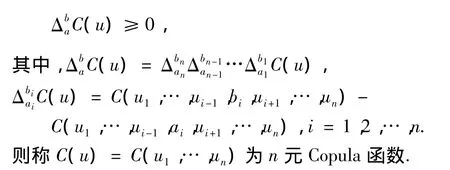
Sklar定理［9］设H是n个随机变量X1，X2，…，Xn的联合分布函数，且这n个随机变量的分布分别为F1，F2…，Fn，必存在一个n元 Copula函数C(称之为随机变量X1，X2，…，Xn的联接函数Copula)，对任意 x=(x1，x2，…，xn)∈ In都有

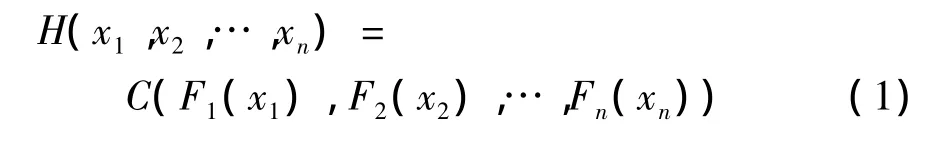
若F1，F2，…，Fn都是连续函数，那么Copula函数C是唯一确定的;反之，若C是n元Copula函数，且F1，F2，…，Fn是分布函数，那么由式(1)定义的函数H是一个以F1，F2，…，Fn为边缘分布的n元分布函数.

由 Sklar定理可知，Copula函数 C(u1，u2，…，un)将多维联合分布与1维边缘分布联系在一起，是联合分布与边缘分布的联接函数.对于1组边缘分布函数已知的随机变量 Xi(i=1，2，…，n)，当其相依关系确定时，就可通过一个能反映相依关系的Copula函数确定这组随机变量的联合分布.

设由集合{1，2，…，n}的全部置换组成的置换群为 πn，对任意置换 σ ∈ πn，设 Xσ(1)，Xσ(2)，…，Xσ(n)为σ作用X1，X2，…，Xn后得到的随机变量，则称X1，X2，…，Xn的联合分布函数H是可交换的，当且仅当对∀σ∈πn，有

H(x1，x2，…，xn)=H(xσ(1)，xσ(2)，…，xσ(n))，即X1，X2，…，Xn和Xσ(1)，Xσ(2)，…，Xσ(n)的联合分布函数相等.

定义3［10］若X1，X2，…，Xn的联合分布函数H是可交换的，则对应的Copula函数是可交换的，且F1=F2=… =Fn，即对于可交换的Copula函数必满足

C(u1，u2，…，un)=C(uσ(1)，uσ(2)，…，uσ(n))对∀σ ∈ πn成立.其中，ui∈［0，1］，i=1，2，…，n.

有关Copula函数的详细介绍可参见文献［10］.以下结论均基于假设，各个部件的寿命随机变量是相依的，且有相同的分布函数F(x)，并通过可交换Copula函数衡量其间的相依关系.

定义5［11］设定义在自然数集合N上的实值函数a(k)，对任意k≥2且k∈N满足

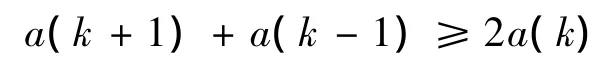
则称函数a(k)是集合N上的离散凸函数.

2 串联系统的随机比较

根据Sklar定理，当已知部件寿命X1，X2，…，Xn的分布时，可由Copula函数或生存Copula函数表示串并联系统寿命的分布函数或生存函数.因此，在串联系统中，非随机n部件系统寿命X1:n的生存函数可以由各个部件寿命的生存函数表示，即

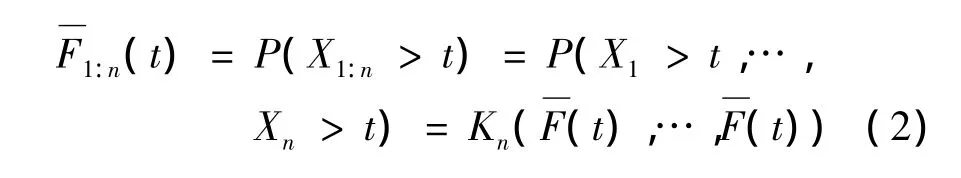
其中，t≥0，Kn(u，…，u)是n元生存Copula函数.

随机N部件系统寿命X1:N的生存函数为

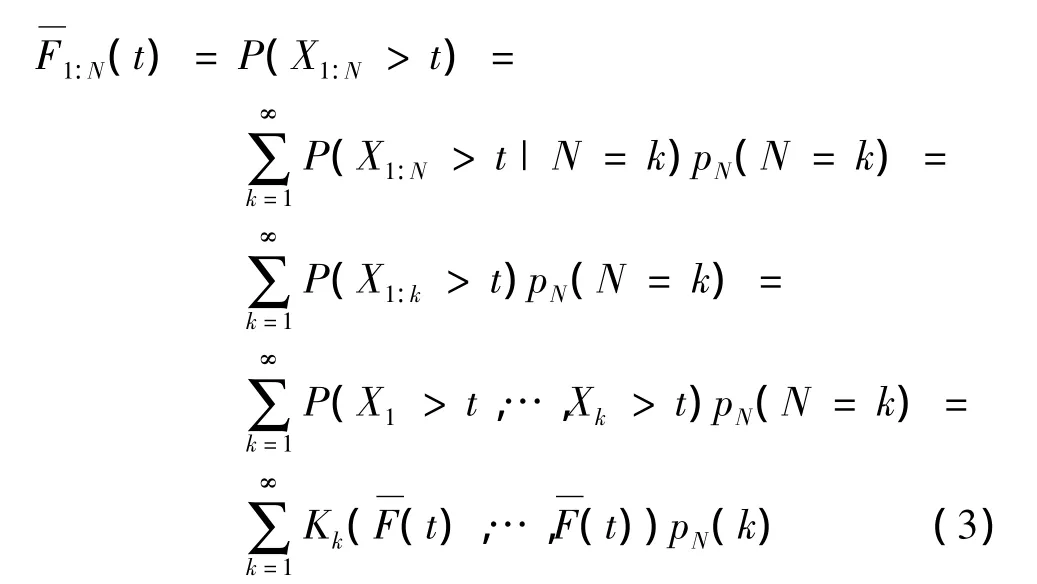
其中，t≥0，k∈N.

此时，要得到关于X1:N和X1:n的随机比较结果，当考虑系统部件寿命是相依的，且相依性由可交换Copula函数度量时，可令u=(t)，则由式(2)和式(3)可知，X1:n和X1:N的生存函数分别为

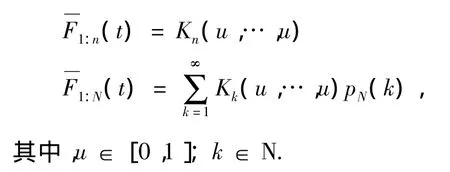
引理 1 设 Kk(u，…，u)=a(k)，即为离散函数，则a(k)是离散凸函数且关于k递减.

【证】首先，证明a(k)关于k递减.

因为Kk(u，…，u)是k元函数，且为k+1元联合生存Copula函数的k元边缘生存函数，因此

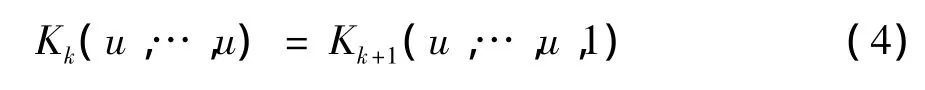
根据式(4)及生存Copula函数的单调性可知

a(k+1)-a(k)=Kk+1(u，…，u，u)-Kk+1(u，…，u，1)≤0，显然，a(k)关于k是递减的.

接着证明，若a(k)是离散凸函数.

当且仅当a(k+1)+a(k-1)≥2a(k)，k∈N且 k≥2，即等价于 Kk+1(u，…，u)-Kk(u，…，u)-Kk(u，…，u)+Kk-1(u，…，u)≥ 0 成 立， 又 因Kk+1(u，…，u，u)是k+1元Copula，所以上式成立.

智能控制比较常见的为模糊控制（包括模糊PID）、神经网络控制（常见BP,RBF）、专家系统、分级递阶控制、学习理论控制（常见PSO,GA以及学习理论-PID模型）。另外，统计学习理论也有用于控制的，典型的是支持向量机回归（SVMR）。

故函数a(k)是离散凸函数且关于k递减.

引理2(詹森不等式概率论形式) 设函数φ是任意有定义的凸函数，对随机变量X，都有不等式

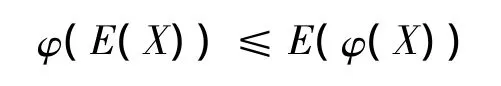
成立，即随机变量期望的凸函数变换后的值小于等于随机变量凸函数变换的期望值，这对下文定理证明有极大帮助.

定理1 若正整数随机变量N的期望值满足条件E(N)≤n，则X1:N≥stX1:n.

【证】 设Kk(u，…，u)=a(k)，一方面有

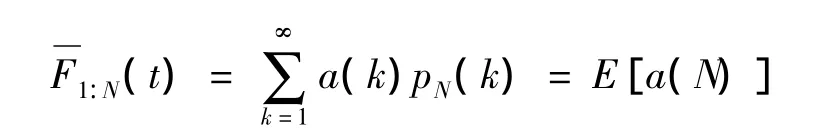
根据引理1，a(k)是离散凸函数，则a(k)满足詹森不等式，即E［a(N)］≥a(E［N］)成立.

另一方面，因为 a(k)关于 k递减，所以当E(N)≤n时，有

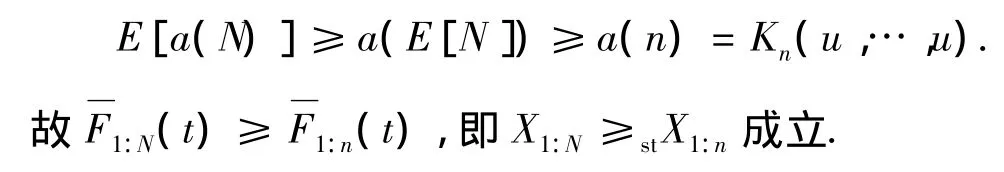
由定理 1可知，当 E(N)=n时，有 X1:N≥stX1:n.下例可验证这一结论.

3 并联系统的随机比较

在并联系统中，非随机n部件系统寿命Xn:n的分布函数为

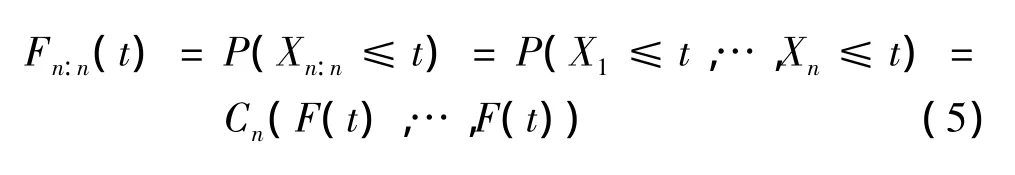
其中，t≥0.

随机N部件系统寿命XN:N的分布函数为

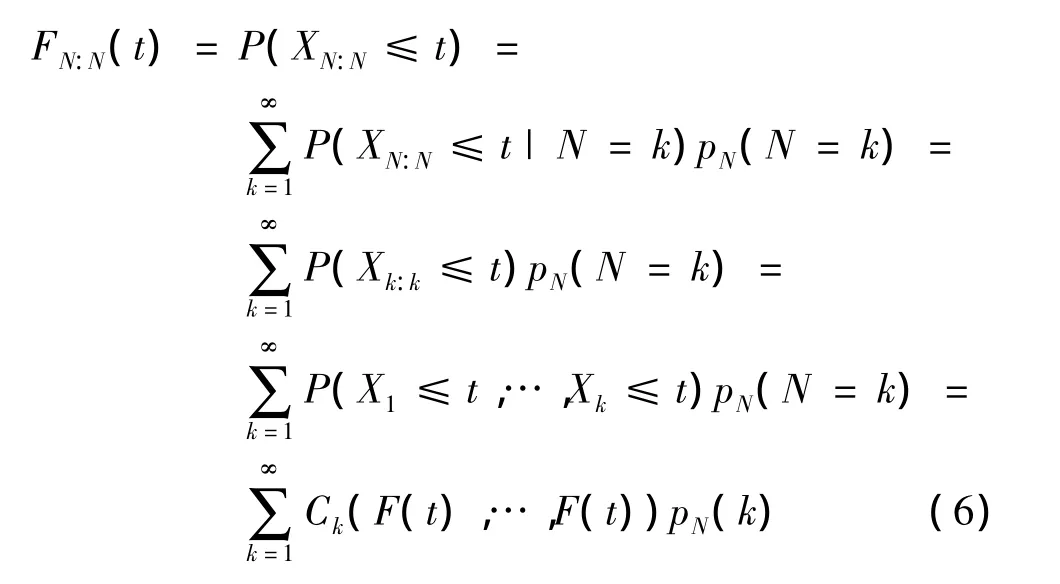
其中，t≥0;k∈N.

这部分将给出并联系统寿命Xn:n和XN:N的随机比较结论.令v=F(t)，根据式(5)和式(6)，则Xn:n和XN:N的分布函数分别为

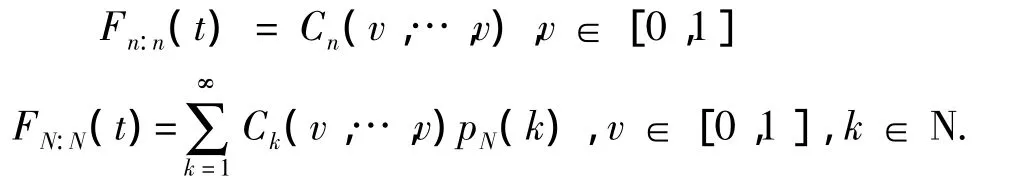
因此对于随机和非随机部件组成的并联系统，其寿命随机变量Xn:n和XN:N有如下的随机比较.

定理2 若正整数随机变量的期望值满足条件E(n)≤n，那么XN:N≤stXn:n.

【证】 令Ck(v，…，v)=a(k)

类似定理1的证明，a(k)是离散凸函数，且关于k递减.

另外，根据詹森不等式和E(N)≤n，可得

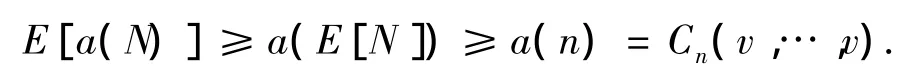
因为FN:N(t)=E［a(N)］和Fn:n(t)=a(n)，

故FN:N(t)≥Fn:n(t).

即XN:N≤stXn:n.

由定理2可知，E(N)=n时，有XN:N≤stXn:n.下例可验证这一结论.

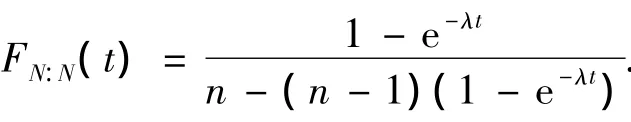
本研究结论可用于不同系统可靠性研究的随机比较.如目前政府和企业部门采取一票否决制决策时，设置投票成员的数量，其可能是固定数字，如n人;也可要求数量在一个区间浮动，即为满足一定条件的随机变量.所以这两种设置成员数量的方案对项目投票结果的影响以及该选择何种方案，本研究在一定条件下可给出答案.

结 语

本文研究当随机部件和非随机部件的寿命是相依同分布时，由其构成的串并联系统寿命的随机比较.结论表明，在串联系统中，当随机数与非随机部件个数间满足E(N)≤n时，随机部件系统的寿命以一般随机序优于非随机部件系统;在并联系统中，当E(N)≤n时，非随机部件系统的寿命以一般随机序优于随机部件系统的寿命.

/References:

［1］Raghunandanan K，Patil S A.On order statistics for random sample size ［J］.Statistica Neerlandica，1972，26(4):121-126.

［2］Gupta D，Gupta R C.On the distribution of order statistics for a random sample size ［J］.Statistica Neerlandica，1984，38(1):13-19.

［3］Rohatgi V K.Distribution of order statistics with random sample size［J］.Communications in Statistics-Theory and Methods，1987，16(12):3739-3743.

［4］Consul P C.On the distributions of orders statistics for a random sample size ［J］.Statistica Neerlandica，1984，38(4):249-256.

［5］Shaked M，Wong T.Stochastic orders based on ratios of Laplace transforms［J］.Journal of Applied Probability，1997，34(2):404-419.

［6］Bartiszewucz J.Stochastic comparisons of random minima and maxima from life distributions［J］.Statistics＆ Probability Letters，2001，55(1):107-112.

［7］Shaked M，Wong T.Stochastic comparisons of random minima and maxima ［J］.Journal of Applied Probability，1997，34(2):420-425.

［8］Li Songchen，Li Yupeng，ChenYingyun.Comparisons of series and parallel systems with random and non-random components［C］//International Conference on Quality，Reliability，Risk，Maintenance，and Safety Engineering.Chengdu(China):2013:388-390.

［9］Nelsen R B.An introduction to copulas Lecture Notes in Statistics［M］.New York(USA):Springer-Verlag Press，2006:18-19.

［10］Jorge N，Fabio S.On the relationships between copulas of order statistics and marginal distributions［J］.Statistics and Probability Letters，2010，80(5/6):473-479.

［11］Qi Feng，Guo Baini.Monotonicity of sequences involving convex function and sequence［J］.Mathematical Inequalities and Applications，2006，9(2):247-254.

2013-06-29;Revised:2013-11-11;

2014-01-05

Comparisons of series and parallel systems with random and non-random dependent components

Li Songchen，Li Yupeng，Chen Yingyun，and Wei Zhenghong†

College of Mathematics and Computational Science，Shenzhen University，Shenzhen 518060，P.R.China

Stochastic comparisons of series and parallel systems composed of random N and non-random n components were studied by implementing an exchangeable copula function.This copula function measures the dependence among the lifetime of each component in the series and parallel systems.By the use of the convexity of discrete functions and the Jensen inequality，when the random variable N satisfies E(N)≤n，we show that the lifetime of a series system composed of random N components is better than that of the system composed of non-random n components under the usual stochastic order;meanwhile，the lifetime of a parallel system composed of non-random n components is better than that of the system composed of random N components under the usual stochastic order.

application of statistical mathematics;reliability theory;order statistics;exchangeable copula;series and parallel system;usual stochastic order;Jensen inequality;discrete convexity

O 211.9

A

10.3724/SP.J.1249.2014.03312

Foundation:National Natural Science Foundation of China(71101095)

†

Professor Wei Zhenghong.E-mail:zhhwei@szu.edu.cn

:Li Songchen，Li Yupeng，Chen Yingyun，et al.Comparisons of series and parallel systems with random and non-random dependent components［J］.Journal of Shenzhen University Science and Engineering，2014，31(3):312-316.(in Chinese)

国家自然科学基金资助项目 (71101095)

李松臣 (1978—)，男 (汉族)，湖北省洪湖市人，深圳大学讲师、博士.E-mail:lisongchen@szu.edu.cn

引 文:李松臣，李育鹏，陈迎运，等.随机和非随机部件组成的串并联系统寿命比较［J］.深圳大学学报理工版，2014，31(3):312-316.

【中文责编:方 圆;英文责编:海 潮】