基于分层阿基米德Copula的金融时间序列的相关性分析
2014-05-12张连增
张连增,胡 祥
(南开大学 经济学院,天津 300071)
基于分层阿基米德Copula的金融时间序列的相关性分析
张连增,胡 祥
(南开大学 经济学院,天津 300071)
与阿基米德copula相比,分层阿基米德copula(HAC)的结构更具一般性,而相比于椭圆型copula它的待估参数个数更少。用两阶段极大似然法来估计HAC函数,主要的步骤是先估计出每个分量的边际分布,以此为基础再估计copula函数。实证分析中,采取Clayton和Gumbel型的HAC分析四只股票价格序列之间的相关性。在得出HAC的结构和估计其参数之前,运用ARMA-GARCH过程消除了序列的自相关性和条件异方差。通过比较赤迟信息准则,认为完全嵌套的Gumbel型HAC能更好地刻画这种相关性。
分层阿基米德copula;两阶段极大似然法;ARMA-GARCH过程;金融时间序列
一、引 言
在量化风险管理中,如何有效地刻画多个金融资产之间的关系始终是研究的热点问题。copula作为分析多个随机变量之间相关性的有效工具,在该领域有着广泛的应用,引起了广泛的关注。
Jondeau等利用t-copula分析了4个股票市场价格指数之间的相关性[1];针对17个国家交易所交易指数基金数据,Serban等分别用多维BEEK和copula模型分析了该组数据的特征,认为copula模型更能描述数据之间的相关性[2];Sun等研究了基于copula-ARMA-GARCH模型的多只股票价格的尾部相关性[3];Patton则提出用时变copula分析时间序列之间的动态关系[4]。基于copula的时间序列的专著,可以参考Patton的研究[5]。
以上研究中,学者们使用的copula函数类主要有椭圆型copula、阿基米德copula。这两种copula函数类在数学上具备很多优良的性质,但现实的情况是,这些良好的性质往往会限制它们的应用。例如:对于k维的椭圆型copula,其待估参数的个数有k(k+1)/2个并且边际分布通常限定为椭圆型分布;对于任意维数的阿基米德copula,它满足交换律并且通常只需要估计一个生成元即可,因为各个分量之间的相关性是完全相同的[6]1-269。
本文引入一类更适用的copula函数类,即分层阿基米德copula。一方面,与椭圆型copula相比较,其待估参数的个数较少,并且边际分布的选取更广泛;另一方面,较之阿基米德copula,分层阿基米德copula的各个分量之间的相关性可以不同,两两之间的相依结构可以是不同的。
二、分层阿基米德copula
分别用 AC(Archimedean copula)和 HAC(hierarchical Archimedean copula)表示阿基米德copula和分层阿基米德copula。在引入HAC之前,先给出copula函数和AC的定义。
对于k维连续联合分布函数F,其相应的copula函数C:[0,1]k→[0,1]可表示为:

图1给出了4维AC、全嵌套HAC和部分嵌套HAC的结构图及相应的参数,需要说明的是在该图中并没有指定生成元的函数的类型。


33图1 AC与HAC结构图
理论上,对于维数为k的HAC,需要确定其最优的结构,但是随着k的增加,可能的结构有2k-k-1个,筛选的过程将很复杂[8]。在实际应用中,通常以完全嵌套的HAC作为备选的结构并且假定其生成元的函数类型是相同的,其原因是:(1)完全嵌套的HAC的结构最具一般性,任何一个部分嵌套的HAC都可以视为其特例,见图1;(2)在金融时间序列建模时,如果提高估计的精度,在生成元函数相同的情况下,那么多个资产两两之间的相关性参数可以认为是完全不同的。鉴于此,本文用完全嵌套的HAC来研究金融时间序列之间的相关性。
三、分层阿基米德copula的估计
关于copula理论的一个重要的研究内容是关于其估计的问题。copula函数的估计方法有很多,如广义矩方法和极大似然法。在理论上,与广义矩方法相比,极大似然法得出的估计量具备有效性和相合性的特征,应用会更加广泛,因此本文只讨论基于极大似然法的完全嵌套 HAC的估计[9]1-111。
极大似然法的基本步骤是,首先构建对数似然函数,然后通过极大化该函数得出相应的参数的估计值。由于copula函数的估计问题既涉及到每个随机变量的边际分布又要考虑其联合分布,因此极大似然法又可以分为一阶段极大似然法和两阶段极大似然法。前者的主要思路是通过一步极大化的过程,同时估计出边际分布的参数和copula函数的参数;而两阶段极大似然法是先估计出每个变量边际分布的参数,然后将其代入copula函数,再估计相应的copula的参数。本文只讨论两阶段极大似然法。

需要指出的是,在上述方法中,第一阶段是通过参数的方法来估计边际分布Fi(xi;αi),当然也通过非参数的方法估计Fi,随后在已知边际分布的基础上,估计出copula的参数θi,i=1,2,…,k。按照这里所说的边际分布估计方法的不同,一般称前者为copula函数的参数估计方法,后者为copula函数的半参数估计方法。
四、实证分析
现用HAC分析A股市场四只股票:贵州茅台、海通证券、建设银行和中国人寿的相关性,股票的选取完全是随机的。价格样本取值于2010年4月9日至2013年4月8日每个交易日的收盘价,数据来自于锐思数据库。考虑到股票交易时,某些股票会在一段时间出现停盘的情况,为保证这四只股票的样本容量的一致,将在某一天至少有一只股票停盘时的数据删除,这样共获取了693个交易日数据。另外,需要指出的是,本文实证分析部分所得出的结果,都是通过R软件的fGarch包、copula包和HAC包实现的。
(一)ARMA-GARCH模型
在分析这四只股票收益率之前,先引入ARMA-GARCH模型。研究表明,ARMA-GARCH模型能够很好地消除序列相关性并且能描述序列的异方差特征[10]183-191。

由于金融时间序列往往存在尖峰厚尾的特征,在式(9)中,νt的分布函数类型并不仅仅局限为正态分布。更一般地,νt可以服从t分布、有偏的t分布或者广义误差分布(GED),这三个分布都具有比正态分布更厚的尾部。事实上,只有准确地拟合了νt的分布才能得出Rt的分布。正如在前文所介绍,拟合νt的分布可以看作两阶段极大似然法的第一阶段。


图2 四只股票价格和对数化收益率的趋势图
选取Series 1作为研究对象,首先确定ARMA过程的阶数以消除序列的自相关性,其次确定GARCH的阶数以克服残差序列的异方差性,最后得到νt的分布。至于Series 2、Series 3和Series 4的分析过程是类似的,本文只给出估计的结果。
图3是{R1,t}的自相关图和偏自相关图。从图3可以看出,该系列存在自相关。同时,在表1中计算了{R1,t}的滞后多期的Ljung-Box统计量的值和相应的p值。Ljung-Box统计量可以作为判断序列自相关的依据。表1的结果显示,各个Ljung-Box统计量的p值较小,可以拒绝原假设,即认为{R 1 ,t}存在自相关。

图3 {R1,t}的自相关图和偏自相关图

表1 {R 1,t}的Ljung-Box检验结果表
用ARMA过程来消除{R1,t}的自相关性时,主要的问题是如何确定ARMA的阶数。本文是通过比较不同阶数的ARMA过程的赤迟信息准则(AIC)和贝叶斯信息准则(BIC)来确定的,见表2。AIC和BIC的值越小,表明ARMA过程拟合的效果越好[5]。表2的结果显示,相比之下,ARMA(1,1)过程效果最好。
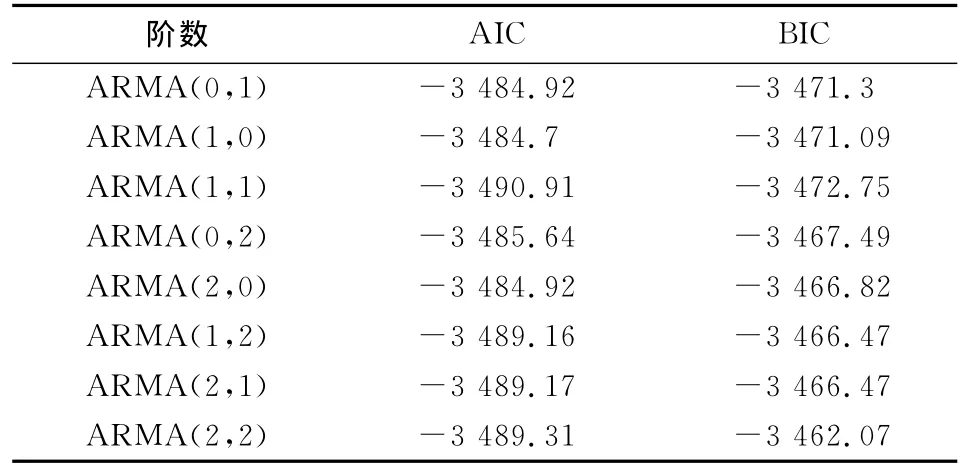
表2 不同阶数ARMA过程的AIC和BIC的值
以ARMA(1,1)模型消除序列{R1,t}的自相关性后,在图4给出{ε1,t}的自相关系数和偏自相关系数图,从图中可以看出{ε1,t}是不相关的。

图4 {ε1,t}的自相关图和偏自相关图

表3 用四种不同分布拟合ν1,t时AIC和BIC的值
基于以上的分析,可以完全确定关于Series 1的ARMA-GARCH模型。类似的方法,可以得出关于Series 2~4的ARMA-GARCH模型。具体的估计结果见表4。在表4中,第一列最后一行的参数η表示t分布的自由度参数;每一行括号内的数值表示相应参数估计的标准差。

表4 用ARMA-GARCH过程估计Series1~4的结果
(二)HAC模型
通过ARMA-GARCH模型估计出四个时间序列的有关参数后,可以进一步得到Ri,t的条件分布Fi:

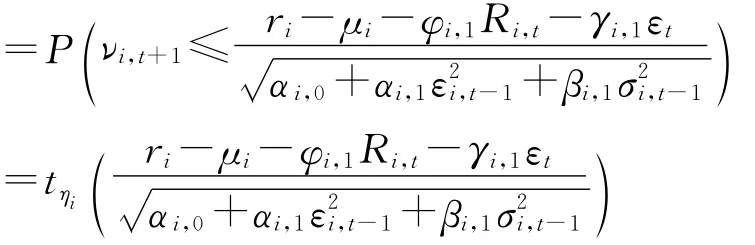
其中i=1,2,3,4,tηi(·)表示自由度为ηi的t分布函数,Fi,t=σ(Ri,s,s≤t)为所有的Ri,s,s≤t所生成的σ代数。这就完成了两阶段极大似然估计的第一阶段。两阶段极大似然法的第二阶段是估计copula函数。鉴于这四个序列两两之间的相关性可能不同(见图2),这里选用完全嵌套的HAC而不是一般的AC进行分析。
将生成元类型固定为Clayton或Gumbel型,那么四元完全嵌套HAC将有三个待估参数,并且这些参数随着HAC层数的递进依次减小,即在HAC的最低层是相关性最强的两个序列构成一个二元AC,依次类推,算法的基本步骤为:

第四步:得出不同生产元的HAC的结构之后,通过AIC的比较,选取AIC的值最小的那个生成元即为最优。
由上述的算法对X1,X2,X3,X4的相关性进行分析,在图5中给出了生成元为Clayton和Gumbel型的完全嵌套HAC的结构。从图中可以看出,无论选取哪一种类型的生产元,HAC的结构是不变的,即中国人寿和海通证券的相关性最强,其次是与建设银行,最后是与贵州茅台。这与我们对图1的观察结果一致,中国人寿、海通证券和建设银行的走势趋同,而贵州茅台的走势呈现不同特征;另外,考虑到中国人寿、海通证券和建设银行同属于金融板块,而贵州茅台来自酿酒板块,因此本文得出的结论符合实情。

图5 完全嵌套HAC的估计结果图
表5给出了生成元为Clayton和Gumbel型的完全嵌套HAC的每一层参数的估计结果和AIC的值,括号内的数值表示参数估计的标准差。表中的^θ(1),^θ(2)和^θ(3)分别表示 HAC 在从最低层到最高层的参数估计值,数值依次减小,通过这些数值可以计算有关的相依系数[6]。最后,通过比较AIC的值判定完全嵌套的Gumbel copula更优。
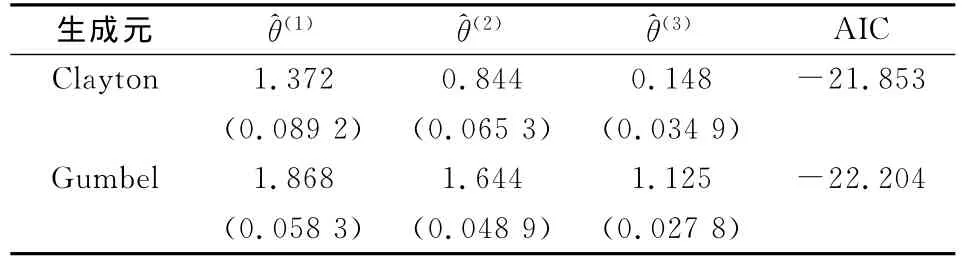
表5 Clayton和Gumbel型的完全嵌套HAC的参数估计结果
五、总结与展望
在描述多个金融资产相关性时,如果选取阿基米德copula或者椭圆型copula,那么就默许了多个资产两两之间的相关性是一样的,这有时与实际情况并不吻合。在本文的实证分析中,就可以看出这种差异性。分层阿基米德copula特别是完全嵌套的分层阿基米德copula能很好地克服这个问题,一方面它能够按照相关性的强弱依次选取变量构成不同的层,另一方面它的结构十分清楚,每一层都构成一个二元的阿基米德copula,并且相关性依次递减。
准确地描述资产之间的关系对决策人确定最优投资组合策略和控制风险具有重要的意义[4]。基于本文所得出的结果,完全确定了每只股票对数化收益率的分布以及它们的联合分布,这样就可以计算相关的风险度量指标,如VaR和TVaR等。
需要指出的是,本文在研究方面存在一定的局限性,以下的后续工作有待研究:一是在更加广泛的函数类里面选取生成元函数,分析分层阿基米德copula的结构并估计有关参数。因为不同的生成元决定了不同类型的copula函数,而不同类型的copula函数刻画着不同的相依结构。二是需要考虑分层阿基米德copula估计方法的稳健性。本文采取两阶段极大似然法估计copula函数,每一阶段的估计效果都对最终结果产生影响。如果在某个阶段估计出现偏差,例如对于本文的实证分析,在第一阶段错误地认为白噪声序列服从的是正态分布而不是t分布,那么基于这样的结论,分层阿基米德copula的结构和参数估计是否会出现偏差?三是准确地度量尾部的风险。本文分析了金融序列整体的相关性,但是对决策者而言,有时候多个金融资产的尾部风险的关系更加重要,然而尾部的数据通常较少,这就需要更有效的方法来捕捉这种尾部相关性。
[1] Jondeau E,Rockinger M.The Copula-garch Model of Conditional Dependencies:An International Stock Market Application[J].Journal of International Money and Finance,2006,25(5).
[2] Serban M,Brockwell A,et al.Modelling the Dynamic Dependence Structure in Multivariate Financial Time Series[J].Journal of time Series Analysis,2007,28(5).
[3] Sun W,Rachev S,et al.A New Approach to Modeling Co-movement of International Equity Markets:Evidence of Unconditional Copula-based Simulation of Tail Dependence[J].Empirical Economics,2009,36(1).
[4] Patton A J.A Review of Copula Models for Economic Time Series[J].Journal of Multivariate Analysis,2012,110(3).
[5] Patton A J.Copula-based Models for Financial Time Series[C].Handbook of Financial Time Series.Berlin Heidelberg:Springer,2009.
[6] Nelsen R B.An Introduction to Copulas[M].2nd ed.New York:Springer,2006.
[7] Savu C,Trede M.Hierarchies of Archimedean Copulas[J].Quantitative Finance,2010,10(3).
[8] Okhrin O,Okhrin Y,Schmid W.On the Structure and Estimation of Hierarchical Archimedean Copulas[J].Journal of Econometrics,2013,173(2).
[9] Trivedi P K,Zimmer D M.Copula Modelling:An Introduction for Practitioners[M].Boston:Now Publishers Inc,2007.
[10]Taylor S J.Modelling Financial Time Series[M].2nd ed.Singapore:World Scientific Publishing,2008.
Dependence Analysis of Financial Time Series Based on Hierarchical Archimedean Copula
ZHANG Lian-zeng,HU Xiang
(School of Economics,Nankai University,Tianjin 300071,China)
In this paper,we introduce the hierarchical Archimedean Copula (HAC)which is more flexible compared with the simple Archimedean Copula,and require a smaller number of parameters compared to elliptical copula.The 2-step maximum likelihood method is discussed which estimates the marginal distribution functions and Copula function,separately.For empirical study,we apply HAC with Clayton and Gumbel generators for modelling the dependence of four stocks,respectively.The ARMAGARCH process is used to model the series correlation and the conditional heteroscadesticity in each financial time series.The best structure and the estimation of the parameters of HAC are also
.In summary,based on Akaike information criterion,we conclude that the fully nested HAC with Gumbel generator exhibits better performance in this case.
hierarchical Archimedean Copula;2-step maximum likelihood method;ARMA-GARCH process;financial time series
F224.0∶O212.1
A
1007-3116(2014)06-0034-07
2013-12-06
中央高校基本科研业务费专项资金《金融工程与精算学中的定量风险管理统计模型与方法》(NKZXTD1101);国家自然科学基金面上项目《非寿险定价与索赔准备金评估的分层模型研究》(71271121)
张连增,男,山东莱芜人,理学博士,教授,博士生导师,研究方向:风险管理与精算;
胡 祥,男,安徽安庆人,博士生,研究方向:风险管理与精算。
(责任编辑:崔国平)
