ADF模式中漂移项和趋势项检验量分布与Bootstrap检验研究
2014-05-12江海峰陶长琪陈启明
江海峰,陶长琪,陈启明
(1.安徽工业大学 商学院,安徽 马鞍山 243002;2.江西财经大学 信息管理学院,江西 南昌 330013)
ADF模式中漂移项和趋势项检验量分布与Bootstrap检验研究
江海峰1,陶长琪2,陈启明1
(1.安徽工业大学 商学院,安徽 马鞍山 243002;2.江西财经大学 信息管理学院,江西 南昌 330013)
在推导ADF检验模式下趋势项和漂移项伪t检验量极限分布基础上,提出修正的系数检验量。研究表明,它们与DF检验模式下检验量具有相同的极限分布;构造漂移项和趋势项检验的Bootstrap实现方法并证明了有效性。将蒙特卡洛模拟技术与临界值检验方法进行对比,结果表明Bootstrap方法能够明显降低检验的水平扭曲,在检验功效方面也有一定优势。模拟也显示临界值检验的局限性和Bootstrap方法的稳健性。
单位根检验;漂移项;趋势项;Bootstrap检验;蒙特卡洛模拟
一、引 言
单位根检验是现代非经典时间序列分析的基础,自Dickey 1976年提出DF检验以来,单位根检验理论不断得到完善和发展,先后提出了30余种检验,其中有6种检验被Eviews软件所采纳[1]。这6种检验的共同特点是在检验前首先要确定数据生成过程(Data Generating Process,DGP),且检验量分布与临界值和DGP一一对应,白仲林等研究表明,确定DGP中是否包括漂移项或者趋势项至关重要[2-3]。为此Compbell等都提出了单位根检验一般过程[4-5]:先从包括漂移项和趋势项的一般模型出发检验单位根,同时对漂移项和趋势项进行联合检验,实际上也可以对漂移项和趋势项直接进行检验。鉴于软件对这两个单参数检验只给出了基于传统t分布①在单位根过程中,除第三种检验,漂移项和趋势项伪t检验量不具有t分布形式,因此检验概率不可用。临界值对应的检验概率,张晓峒等以DF检验为对象按有无漂移项的DGP分别推导了漂移项和趋势项的极限分布,并给出了响应面函数[6];肖燕婷等则以无漂移项DGP估计有漂移项和趋势项模型,并给出了相应的分布②这种DGP情况下检验量的分布与有漂移项DGP情况下在消除共线性后检验量的分布相同。,这无疑丰富了单位根检验理论[7]。然而与单位根检验相关的检验量只在大样本下才有极限分布,Leybourne等对单位根项检验的模拟研究表明,使用有限样本下临界值方法对单位根项进行检验,会产生较大的水平扭曲,并引发功效损失[8]。为了解决这个问题,Basawa等将Bootstrap方法应用到单位根项检验中,取得了较好的检验效果[9-14]。但就漂移项和趋势项的检验而言,仍有以下问题值得进一步思考:
第一:不像单位根项检验那样,既可以使用伪t检验量,也可以采用系数或修正系数检验量③在ADF和PP检验模式下,单位根项系数检验量需分别采用参数和非参数方式进行调整。,张晓峒和攸频的研究以及下文研究都表明,漂移项和趋势项系数检验量不能用于检验,只能采用伪t检验量[6]。那么,是否存在类似可行的修正系数检验量呢?
第二:由于ADF检验允许在数据生成过程中添加差分因变量的滞后期,以降低扰动项可能存在的自相关性,从而更符合实际要求并被广泛使用,但目前尚没有文献研究ADF检验模式中漂移项、趋势项检验量的分布。另外,聂巧平等的研究表明,DF检验模式与ADF检验模式下的联合F检验量有相同的分布[15]。那么,这种等价关系对漂移项与趋势项检验量是否存在呢?
第三:由于模拟次数不同,不同文献给出的相同样本容量和显著性水平下的临界值有明显差异,这表明蒙特卡洛模拟得到的临界值缺乏稳健性。那么,是否存在一种不依赖临界值的检验方法呢?
第四:张晓峒等的研究以及下文都表明,检验水平扭曲和功效损失问题也存在于漂移项和趋势项检验中[6]。那么,能否也使用合适的Bootstrap方法来适当降低检验水平扭曲程度呢?
第五:在蒙特卡洛模拟获取临界值的时候,都毫无例外地假设扰动项服从标准正态分布。那么,由此得到的临界值对扰动项服从其它分布是否具有稳健性呢?
因此,本文将对以上5个问题进行研究。本文创新在于:推导了ADF检验模式下漂移项和趋势项在3种估计情况下伪t检验量的分布,提出了基于Bootstrap方法下修正的系数检验量,拓展了Ferretti等的Bootstrap方法,模拟证实了标准正态分布扰动项对其它分布类型缺乏稳健性,从而为单位根检验理论和Bootstrap方法做了有益的补充。
二、ADF检验模式下伪t检验量与修正系数检验量



提取所要研究的两个估计量可得到式(4)成立。
类似可以提取两个估计量方差的极限分布,进而计算伪t检验量得到式(5)和式(6)。
在式(4)中,由于两个系数检验量都含有未知参数σ,不能直接用于检验,因此本文采用参数σ的一致估计量s1T进行修正。显然,修正后检验量为渐进Pivotal①Pivotal通常被译为轴枢,笔者认为这种译法没有体现出真正含义,因此保留其英文表示,渐进Pivotal检验量表示该检验量的分布在大样本下不含有任何未知的参数。检验量,可用Bootstrap方法进行检验,本文称之为修正系数检验量。
类似地,可以假设无漂移项数据生成过程为:
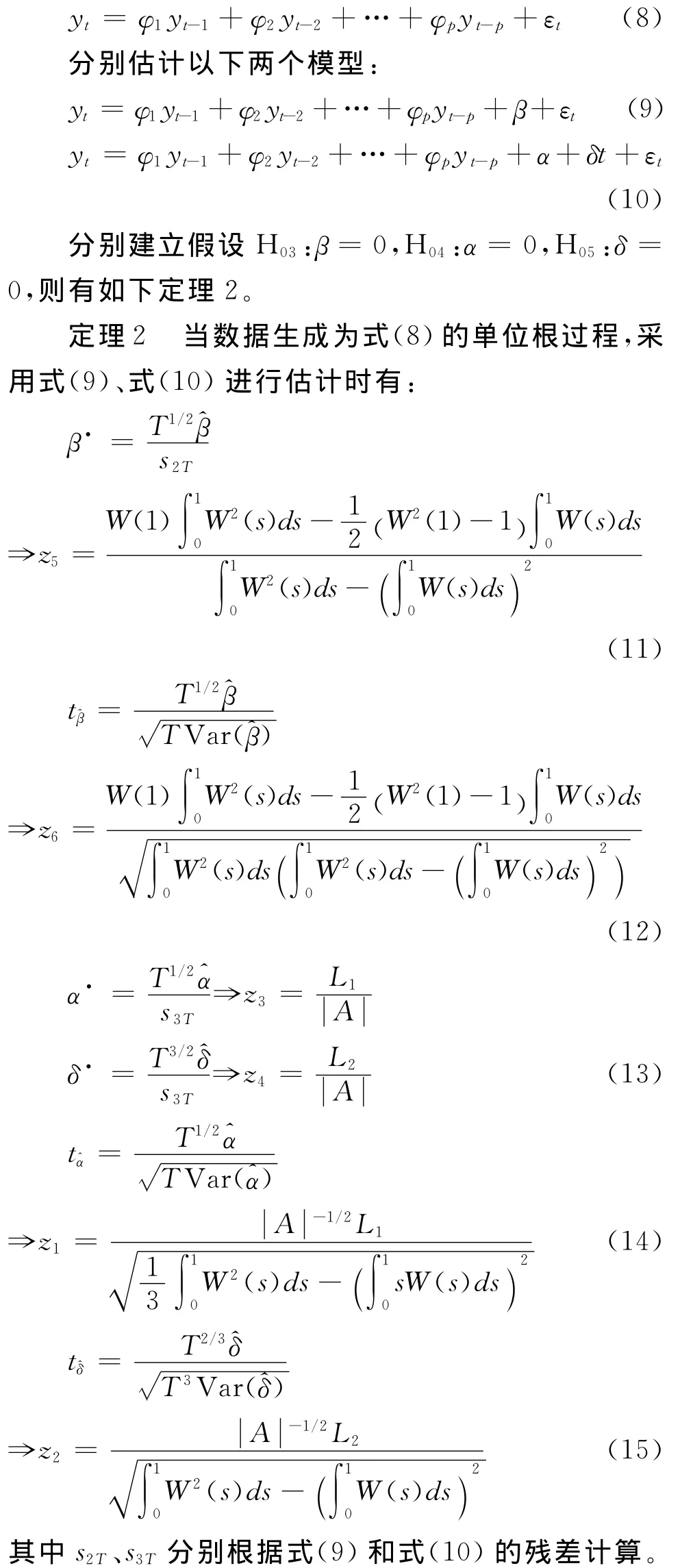
定理2证明过程与定理1类似,限于篇幅略去。
上述式(11)和式(13)就是修正的系数检验量,而式(12)、式(14)和式(15)分别与张晓峒等研究中DF检验模式对应检验量的极限分布相同,因此定理1和定理2不但回答了本文提出的第一个和第二个问题,也为下文的Bootstrap检验提供了方便。
三、Bootstrap检验研究
定理1和定理2表明,两种检验模式下漂移项和趋势项检验量的极限分布完全相同,不失一般性,下面仅以DF检验模式为研究对象,使用Bootstrap方法对漂移项和趋势项进行检验,对于ADF检验模式,只要相应修改本文的Bootstrap方法即可完成检验。根据数据生成过程是否含漂移项分两种情况进行研究。
(一)数据生成无漂移项的Bootstrap检验
设数据生成过程为:

为了说明Bootstrap方法的有效性,就必须从理论上证明基于Bootstrap样本下的检验量与原始样本对应的检验量具有相同的极限分布,证明过程中将使用大数定律、中心极限定理、连续映射定理、Bootstrap不变原理以及Slutsky定理。首先构造如下部分和序列:

① 的表达式参见文献[11],引理2的证明也参考该文献。② 为方便起见,Bootstrap样本下各个检验量都省略了下标b,例如简记为,其它也是如此。

(二)数据生成有漂移项的Bootstrap检验
设数据生成过程为:
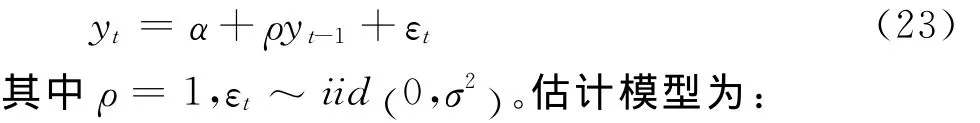

① 实际进行检验时,为了消除共线性需要对模型作处理,可参考文献[6]中的做法,在Bootstrap样本下消除共线性需要使用估计量^α来进行。
再根据引理1、引理2、连续映射定理、大数定律和Slutsky定理有:
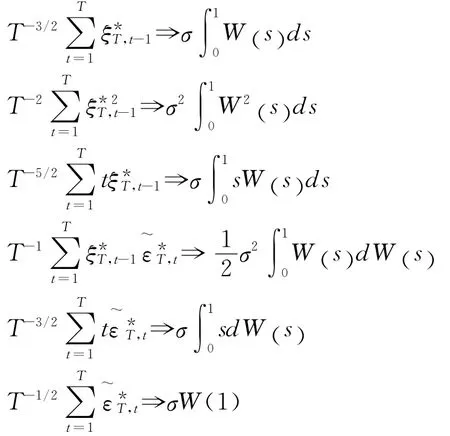
利用OLS估计式(25)并结合上述分布有①在DF检验模式下,式(26)、(27)中的λ=σ。:

因此,定理3和定理4从理论上证实了可以使用Bootstrap方法根据自身样本来提取临界值进行检验,而不必使用扰动项基于标准正态分布强假定下得到的临界值,这就回答了本文的第三个问题,也部分回答了第四个问题。
四、蒙特卡洛模拟研究
为了进一步回答本文的第四个问题并考察第五个问题,现进行蒙特卡洛模拟分析。为了考察误差项分布的不同对临界值检验是否有影响,选取标准正态分布、均匀分布U(0,1)和自由度为5的卡方分布,分别记为类型1、类型2、类型3,对于后两种分布的期望需要进行中心化处理;为了考察样本因素,选取了4种样本,分别为15、25、40和60,临界值分别来自张晓峒和肖燕婷等的研究,取显著性水平为0.05;在式(23)中取α=1,设定Bootstrap样本构造次数和蒙特卡洛模拟次数均为15 000。首先分析在数据生成过程为单位根下的结果,检验结果如表1和表2所示。

表1 无漂移项数据生成模型下的检验水平结果 单位:%

表2 有漂移项数据生成模型下的检验水平结果 单位:%
可以从两个角度来评价两种检验方法的优劣:首先,比较两种检验方法与显著性水平的吻合程度,即可靠性。根据Godfrey和Orme提供的实际显著性水平区间估计公式,取概率度为1.96得到实际显著性水平的区间估计为(4.65%,5.35%)[17]。按此标准,在表1中使用临界值进行检验时,有11个检验落在区间之外(表1中用加粗表示,表2也相同),实际覆盖率为69.44%;而使用Bootstrap方法进行检验时,所有检验都落在区间内,具有100%的覆盖率,显示出该方法较临界值方法的优越性。以上11种情况的样本分布为3:2:1:5,这表明即使增大样本,水平扭曲程度并没有呈现降低趋势;在三种误差类型中的分布为4:5:2,分布的不均匀性表明了基于标准正态分布得到的临界值对其它分布误差类型缺乏稳健性,或者说其代表性较差,这就回答了第五个问题。其次,可以考察实际检验水平与名义显著性水平的接近程度,即精确性。表1中显示临界值检验下有21个较Bootstrap方法占优(表1中用下划线表示,表2也相同),剩下的51个检验是Bootstrap方法占优。因此从精确性角度来说,Bootstrap方法总体上也显示出较强的优势。更为重要的是:表1显示在Bootstrap方法下,本文提出的修正系数检验量取得了和伪t检验量相近结果,表明了该检验量的可行性。同样,表2也有上述类似结论,这里不再详细说明。
接下来比较两种方法的检验功效,为此取ρ=0.95来考察两种方法的效果,仍然使用基于单位根下的临界值,且Bootstrap样本的构造也保持不变,此时原假设不成立,因此理想的结果是较高的拒绝率。表3给出了无漂移项数据生成过程下的模拟结果。
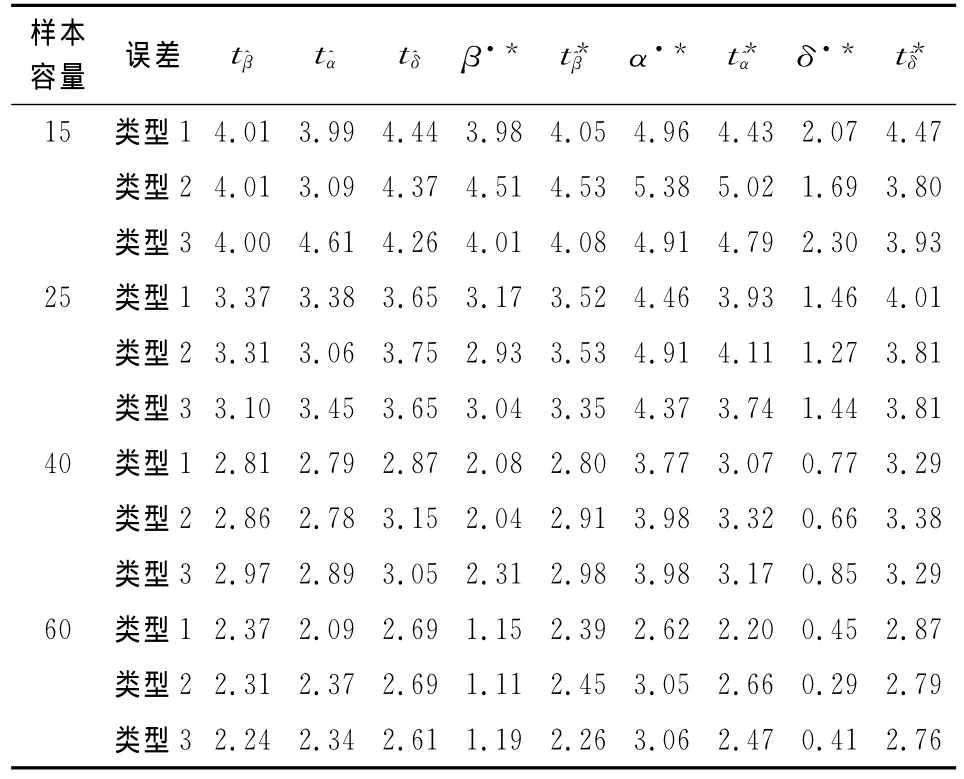
表3 无漂移项数据生成模型下的实际拒绝率 单位:%

表4 有漂移项数据生成模型下的实际拒绝率单位:%
五、结 论
综上研究,本文得到了以下四点结论:
第一,就修正的系数检验量而言,当数据生成为单位根过程时,修正系数检验量的实际检验水平与名义显著性水平相吻合,具有满意的检验效果;在近单位根过程的检验中,虽然趋势项的修正系数检验量在绝大多数场合下有较低的拒绝率,但漂移项的修正系数检验量具有较高的拒绝率,因此修正系数检验量也可以用于检验。
第二,就检验量分布而言,基于ADF检验模式下漂移项和趋势项检验量的极限分布与DF检验模式下对应检验量的极限分布相同,因此实证分析中可以使用已有文献给出的临界值。
第三,就检验的可靠性和精确性而言,蒙特卡洛模拟研究表明,两个指标都显示出Bootstrap方法较临界值方法有优越性,具有更低的水平扭曲;在检验功效方面,临界值方法与Bootstrap方法各有优势,因此Bootstrap方法可代替临界值方法进行检验。
第四,就误差类型对检验的影响而言,模拟研究表明,基于标准正态分布扰动项假设下得到的临界值缺乏稳健性,因此当实证分析中的数据不满足假设条件时,临界值检验得到的结论需谨慎对待,此时需要借助Bootstrap方法进一步检验。
最后需要指出的是,不像平稳时间序列那样,可以借助Edgeworth展开式从理论上证明有限样本下Bootstrap方法优于渐进分布的临界值方法。由于单位根检验所涉及的检验量是维纳过程的泛函,很难获得Edgeworth展开式所需要高阶矩结果,因此目前还不能从理论上给出明确的证明,但已有文献和本文的模拟结果都表明了Bootstrap方法较临界值方法有优越性。
[1] Dickey D A.Estimation and Hypothesis Testing in Nonstationary Time Series[D].Ames,IA,Ph.D.Thesis of Iowa State University,1976.
[2] 白仲林,赵嫣.检验式设定错误对时间序列单位根检验小样本性质的影响[J].统计与信息论坛,2008(4).
[3] 陶长琪,江海峰.二次趋势模型的误设检验与仿真分析[J].统计与信息论坛,2012(3).
[4] Campbell J Y,Perron P.Pitfalls and Opportunities:What Macroeconomists Should Know about Unit Roots[J].NBER Macroeconomics Annual,1991(6).
[5] Doldado Juan,Tim Jenkinson,Simon Sosvilla-Rivero.Cointegration and Unit Roots[J].Journal of Economic Surveys,1990,4(3).
[6] 张晓峒,攸频.DF检验式中漂移项和趋势项的t统计量研究[J].数量经济技术经济研究,2006(2).
[7] 肖燕婷,魏峰.单位根DF检验中漂移项、趋势项的分布特征[J].重庆工学院学报:自然科学版,2008(7).
[8] Leybourne S,Newbold P.On the Size Properties of Phillips-Perron Tests[J].Journal of Time Series Analysis,1999(1).
[9] Basawa I V,Mallik A K,McCornick W P,et al.Bootstrapping Unstable First-order Autoregressive Processes[J].Annals of Statistics,1991,19(2).
[10]Basawa I V,Mallik A K,McCornick W P,et al.Bootstrap Test of Significance and Sequential Bootstrap Estimation for Unstable First Order Autoregressive Processes[J].Communications in Statistics-Theory and Methods,1991,20(3).
[11]Ferretti N,Romo J.Unit Root Bootstrap Tests for AR(1)Models[J].Biometrika,1996,83(4).
[12]Richard P.Modified Fast Double Sieve Bootstraps for ADF Tests [J].Computational Statistics and Data Analysis,2009(12).
[13]刘汉中.残差块形自助法在非对称单位根检验中的适用性[J].统计与信息论坛,2010(2).
[14]Mantalos,Karagrigoriou A.Bootstrapping the Augmented Dickey-Fuller Test for Unit Root Using the MDIC[J].Journal of Statistical Computation and Simulation,2012,3(82).
[15]聂巧平,张晓峒.ADF单位根检验中联合检验统计量研究[J].统计研究,2007(2).
[16]陆懋祖.高等时间序列经济计量学[M].上海:上海人民出版社,1999.
[17]Godfrey L G,Orme C D.Controlling the Significance Levels of Prediction Error Tests for Linear Regression Models[J].Econometrics Journal,2000,3(1).
Distribution of Statistics of Drift and Time Trend under ADF Mode and Bootstrap Test
JIANG Hai-feng1,TAO Chang-qi2,CHEN Qi-ming1
(1.School of Business,Anhui University of Technology,Ma'anshan 243002,China;2.School of Information and Management,Jiangxi University of Finance and Economics,Nanchang 330013,China)
The paper first derives the limit distribution of pseudo t test for drift and trend based on ADF test mode,and brings forward the modified coefficient test.Results show these tests share the same limit distribution with the DF test mode.Then the Bootstrap test and its validity for drift and trend is given and testified.Results from Monte Carlo Simulation indicate that the Bootstrap method can significantly reduce the size distortion and also has certain advantages in test power over critic value method.Simulation also shows the limitation of the critic value method and the robustness of the Bootstrap method.
unit root test;drift;trend;Bootstrap test;Monte Carlo simulation
O221.6∶F224.0
A
1007-3116(2014)06-0003-08
2013-11-18
国家社会科学基金项目《基于Bootstrap方法下单位根检验研究》(13BJY011)
江海峰,男,安徽巢湖人,博士生,副教授,研究方向:数量理论及应用;
陶长琪,男,江西临川人,经济学博士,教授,博士生导师,研究方向:数量经济学;
陈启明,男,安徽宿松人,管理学硕士,讲师,研究方向:预测与决策,运筹与管理。
(责任编辑:崔国平)
