基于C-W节约算法的物流配送车辆路径问题的研究

赵春阁，徐 群

(1.兰州商学院 信息工程学院;2.兰州商学院工商管理学院，甘肃兰州 730020)

物流配送车辆路径问题(Vehicle Routing Problem，VRP)最早是由Dantzing和Ramser［1］于1959年首次提出的，是近年来各学者研究的重点.其基本定义可以描述为下:有客户若干，他们各自有不同数量的货物需求，由配送中心提供货物，由一个车队负责分配货物，组织适当的行车路线，目标是使客户的需求得到满足，并能在一定的约束条件下，达到目标(路程最短、使用车辆数尽量少、费用最少、耗费时间最少等).

VRP属于NP难题［2］，目前解决VRP的算法主要集中于启发式算法.而启发式算法包括节约算法、模拟退火法、确定性退火法、禁忌搜索法、遗传算法等.每一种算法都存在一定的缺陷，相比其他启发式算法，Clarke和Wright［3］提出的节约算法及其改进算法［4］较为简单清晰明了，对解决日常生活中的简单物流配送路径问题比较适用，国内学者也做了一系列研究，刘诚［5］等研究了具有区间参数的VRP及其改进的C-W节约算法，对费用参数进行排序，并应用了可能度的区间排序方法;孙焰［6］等提出了一种改进的节约算法用来解决配送规划问题，将AK算法与传统的C-W节约算法相结合，避免了某些情况下C-W算法求解结果与最优解相差较大的问题;张建勇［7］等提出了一种具有模糊费用系数的VSP的修正C-W节约算法，在对具有模糊费用系数的车辆调度问题进行简单描述的基础上，构建了模糊车辆调度的数学模型并结合节约算法来解决问题;朱晓兰［8］等提出C-W节约算法在装配企业采购物流中的应用，针对装配企业采购物流中所运输产品的特点，在线路规划中插入车辆载重量和容积的双重约束条件，并验证了C-W节约算法对此问题的适用性.以上研究多证明节约算法的优势，未考虑其局限性.本文针对以上研究存在的问题及物流配送领域的现状，提出一种改良的、简单适用的C-W节约算法，建立了数学模型，并且通过案例分析来优化物流配送路径.

1 VRP问题概述

1.1 问题描述

VRP问题可以描述如下:有一定数量的客户配送中心，负责向各客户运输货物，假设配送中心的编号为0，有N个客户，编号分别为1，2，3，……，N.第i个客户的货物需求量为qi，卸货时间为UTi，客户允许到达的最早时间、最迟时间分别为ETi、LTi.中心与客户、客户与客户两两之间的运输费用Cij，运输时间为 Tij(i=1，2，3，…，n).已知每辆车的载重量都有 Q 的限制(Q 〉 qi，i=1，2，3，…，n)，每辆车不允许超载，而且必须在规定的时间内把货物送到.如果每辆车有工作时限WTk(k=1，2，3，…，k，k表示配送车辆总数).要求指派车并确定每辆车的配送路线，使总的运输费用最低或是运输路径最短.

1.2 问题假设

(1)每辆车必须从配送中心出发，对客户进行配送服务最后再返回配送中心;

(2)要求所有的顾客都被服务，每位顾客一次配送完成;

(3)若在某条配送线路上，i是j前面并且相邻的节点，RTi、RTj分别是到达节点的时间，则它们之间的关系如下:

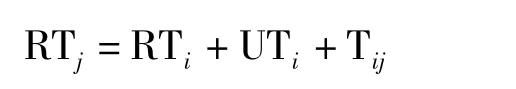
2 建立VRP数学模型

为了建立模型，需要定义如下决策变量:

带工作时限和时间窗约束的模型如下:

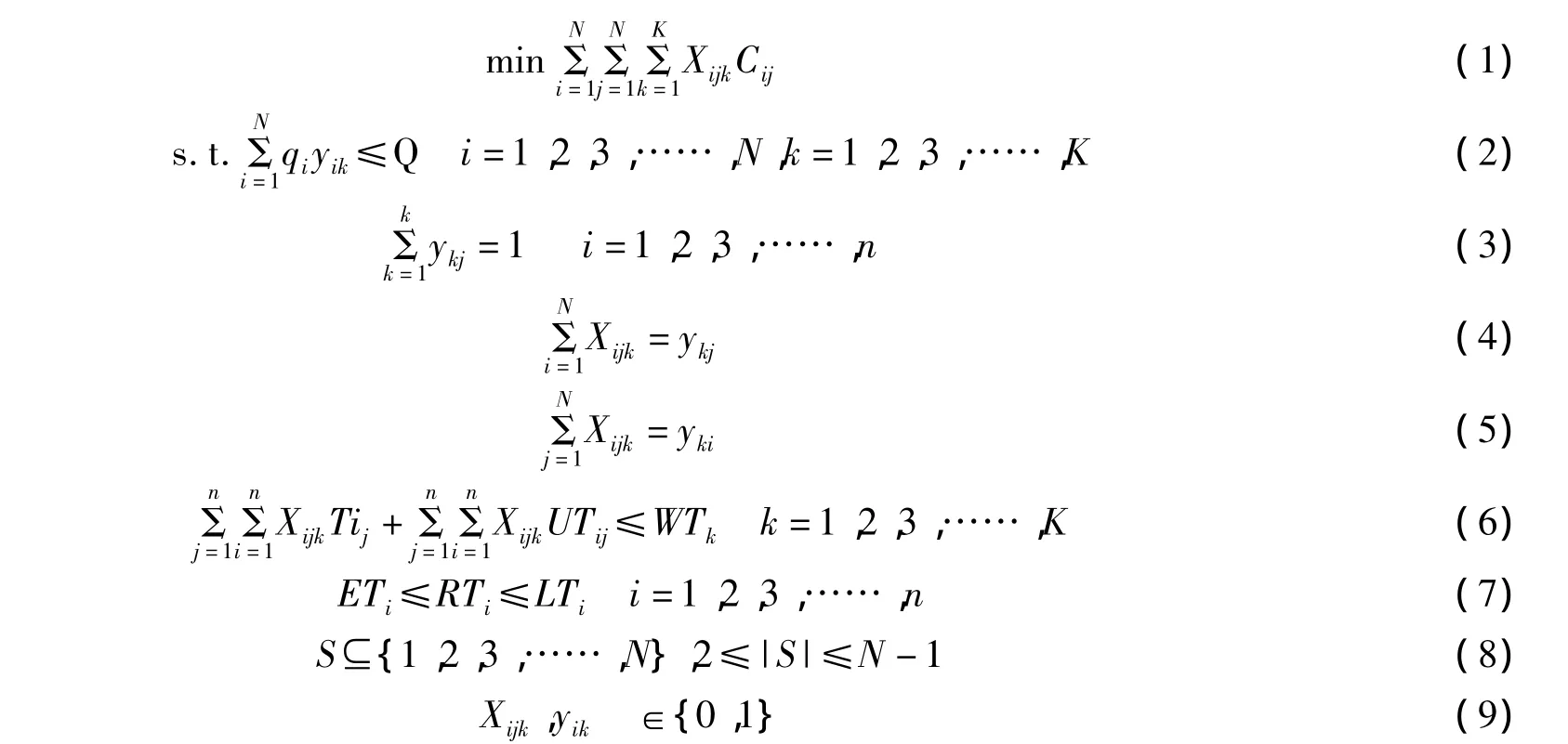
目标函数(1)表示费用最低;约束条件(2)表示每辆车的装载货物不能超过车容量;约束条件(3)表示每个客户点的任务只能由一辆车来完成;约束条件(4)、(5)表示到达和离开某以客户的车辆有且仅有一辆;约束条件(6)表示每辆车的工作时间不能超过最大工作时限;约束条件(7)要求所有车辆都必须在规定的时间内到达，同时还需要保证运输网络必须是联通的;约束条件(8)是用来表示消除之路，以避免出现孤立圈;约束条件(9)是变量取值约束.

3 VRP模型求解

3.1 C-W节约算法

文章将采用C-W节约算法及其改进的算法来求解模型.C-W节约算法的基本思想是:假设首先每辆车从配送中心出发抵达某一个客户，车辆卸货后直接返回配送中心，即构成了n条“0-i-0”(i=1，2，3，……，n)的初始配送路线，第i条路线的运输费用可记为:

然后把客户 i和客户 j连接，形成线路“0-i-j-0”(i，j=1，2，3，…，n)，计算线路连接后到达客户的运输费用的“节约值”:

Y(i，j)越大.说明把客户i和客户j连接在一起用同一条运输路线进行送货时的费用的节约值就越多，因此应该优先连接y(i，j)值较大的i和j点.

3.2 改进的C-W节约算法

由于Clarke-Wright的节约启发式算法简单、交互特性好.在实际应用中非常广泛，但并不是所有的问题都可以简单调用.本文在对C-W算法深入研究的基础上，对其进行改进［9-10］，并在下文中通过实例具体应用了此节约算法.改进的C-W节约算法的步骤如下:

(1)计算 y(i，j)，令 M={y(i，j)|y(i，j)〉0，i，j=1，2，3，…，n}，并把集合 M 的元素按从大到小的顺序排序，转(2);

(2)选择集合M的第一个元素y(i，j)，考察点i和j，如果满足点i和j均在初始化线路上，或者是点i和点j有一个在已构成线路上且与配送中心相连，另一个在初始化线路上，或者点i和点j位于不同的已构成线路上，但都与配送中心相连，则转(3)，否则转(8);

(3)计算连接点i和j后车辆的货运量NQ，若NQ≤Q，转(4)，否则转(8);

(4)计算连接点i和j后线路总的工作时间NW，若NWT〈WT，转(5)，否则转(8);

(5)根据式(1)计算连接i和j后到达m点(m点为连接前包含j的线路上的个点)的时刻RTm，若ETm≤RTm≤LTm，则转(6)，否则转(8);

(6)连接点i和j，计算车辆到达各个客户的时间，转(7);

(7)如果本线路与其他任何一条线路连接后，若货运量都大于车的载重量或车的工作时间都大于工作时限，则转(9)，否则转(8);

(8)在集合M中消去这个最大元素y(i，j)，转(10);

(9)在集合M中消去所有包含本线路上任一点的元素，转(10);

(10)如果M=Ø算法结束，否则回到(2);

4 实例验证

为了使模型和算法体现的较为明了，本文给出一个简单易懂的实例介绍.假设某配送中心有一定配送任务，现有5个客户，各任务货运量为Ri(见表1，图1)，配送中心0有5辆载重量为4t的货车.最大运输距离为40km.车辆由配送中心0出发.各客户之间的距离可由表2给出.

表1 配送中心配送任务表

表2 各项任务点之间的距离

(1)计算各个用户连接之间的费用“节约值”，y(i，j)=C0j+Cj0-Cij.比如连接用户1和用户2，y(1，2)=C01+C20-C12=10+13-5=18.类似的，连接其他各用户，可以得到相应的“节约值”，按照“节约值”从大到小的顺序排序，见表3.

表3 节约里程排序表

(2)构造线路

①从最大的里程“节约值”y(i，j)开始考虑各用户.由表3可知，y(3，4)最大，连接用户3和用户4，得到线路0-3-4-0，此时线路上的任务量为1.9+1.8=3.7〈4.下一个大的里程“节约值”是y(2，4)，若连入，则任务量为3.7+2〉4，故不能连接，同理也不能与其他用户连接，此时得到了第一条线路，里程“节约值”为23.

②由表3可知，接下来考虑y(1，2)，得到线路0-1-2-0，此时线路上的任务量为1+1〈4.下一个被配送客户的里程“节约值”大的是y(1，5)，线路上的任务量为2+1.5〈4，则可连入，得到第二条线路，里程“节约值”为18+1=19.

至此，所有用户均被包围在线路中，共两条线路，分别是0-3-4-0，0-5-1-2-0，共用两辆车.总的里程为10+7+20+10+5+13+2×6=77km，节约里程为23+19=42km.可见若采用此种方法，可以大大提高物流效率，大幅度降低业务成本.

为了进一步分析此算法的适用性，将客户规模增至8，货车数量也增至为8辆，其他保持不变，客户6、7、8 的货运量依次为0.9、1.5、2.各客户点分布图如图 2.

图1 各客户点分布图

图2 各客户点分布图

根据 C-W 节约算法计算，最终得0-3-4-0，0-1-2-0，0-6-7-0，0-5-0，0-8-0，共5 条线路，用5辆车，从计算结果可以看出，此次优化结果并不理想，客户5、客户8并没有被优化，而是单独配送的.此算例表明随着解的空间的增加，解的精确度也逐渐下降，出现了不理想的情况.从而证明，此改良的C-W算法对解决客户数量较少的物流配送问题有较高的适用性.但是随着客户规模的增加，此算法则有一定的局限性.

5 结语

本文深入研究了基于C-W节约算法的物流配送车辆路径问题，通过一种改良的节约算法得到优化配送路线，并通过具体实例验证了该算法的适用性及局限性.C-W节约算法求解速度快、通用性强、限制条件易于加入，优先考虑一些配送中心较远的需求点是一种相当实用的启发式算法，为该领域的进一步发展奠定了一定的基础.但是，对于一些客户规模大的问题，此算法则没有优越性，需要考虑其他的启发式算法.

［1］DANTZIG G，RAMSER J.The truck dispatching problem［J］.Management Science，1959(6):80-91.

［2］Garey M R，Johnson D S.Computers and Intractability:A Guide to Theory of NP-Completeness［M］.San Franciscon:W.H.Freeman and company，1979.

［3］Clarke G，Wright J.Scheduling of vehicles from central depot to a number of delivery points［J］.Operations Research，1964(12):568-581.

［4］林晓宁，李金铭，纪寿文.车辆路径问题Clarke-Wright算法的改进与实现［J］.交通与计算机，2004，22(6):72-75.

［5］刘诚，顾坤坤.具有区间参数的VRP及其改进的C-W节约算法［J］.武汉理工大学学报，2010，32(2):182-185.

［6］孙焰，张喆.一种解决配送规划问题的改进节约算法［J］.物流科技，2009，29(9):29-31.

［7］张建勇，郭耀煌，李军.一种具有模糊费用系数的 VSP的修正C-W节约算法［J］.西南交通大学学报，2004，39(3):281-284.

［8］朱晓兰，赵一飞.C-W节约算法在装配企业采购物流中的应用［J］.上海交通大学学报，2007，41(9):1420-1424.

［9］Ballou Ronald H.Business logistics Mangement:Planning，Organizing，and Controlling the Supply Chain(4th Edition)［M］.Upper Saddle River，NJ:Prentice-Hall，1999.

［10］刘志强，丁鹏，盛焕烨.物流配送系统设计［M］.北京:清华大学出版社，2004.