中心对称量子态的量子失协
2014-05-11
(上饶师范学院,江西 上饶 334001)
引言
量子失协是比量子纠缠更广泛的一类量子关联。在量子信息、量子计量、凝聚态物理等学科中有重要应用[1,2]。计算量子失协是一个比较困难的问题,即使一个一般的两比特量子系统也没有一个完整的解析公式。已有的结果包括诸如限制在著名的“Χ”态等。“Χ”态是一个4×4的只有对角线和反对角线上存在非零值的密度矩阵。文[3,4]介绍了它的代数性质和关于量子失协解析公式的相关结果。“Χ”态密度矩阵包含了许多有名的量子态,诸如Bell对角态,Werner态,Isotropic态等等。n×n中心对称态密度矩阵满足:aij=an-i+1,n-j+1。在本文中我们通过局域正交变换建立中心对称态和“Χ”态之间的联系,得到了中心对称态密度矩阵的量子失协的解析公式。
1 中心对称态和“Χ”态密度算子
量子力学中密度算子必须是厄米、非负并且迹为1的一个方阵。一个一般的4×4中心对称态记为
(1)
其中p1,…,p7为参数。对双量子比特“Χ”态,我们有
(2)
其中q1,…,q7为实参数,考虑如下双Hadamard变换
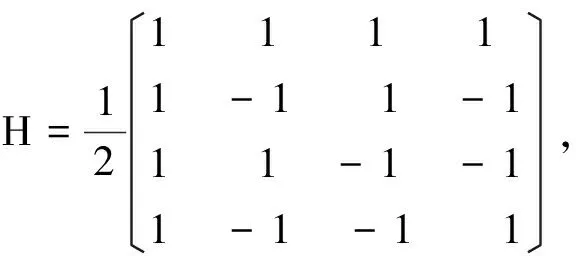
(3)
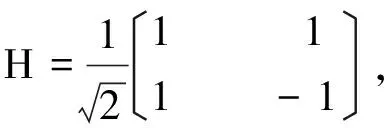
(4)
为Hadamard变换。矩阵R为实对称正交阵。
由(1)-(3)我们有如下关系:
H⊗HρcH⊗H=ρx
(5)
且
H⊗HρxH⊗H=ρc
(6)
这里它们之间的矩阵元素有如下关系
Imp14=-Imp41=q5=-p3-p5,
Imp23=-Imp32=q7=-p3-p5
(7)
反之,
(8)
将ρc用Pauli矩阵展开可得
(9)
对ρc实行Hadamard变换可得
(10)
事实上,由ρx的Bloch表示,我们有
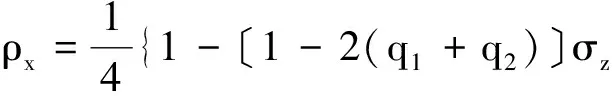
〔1-2(q2+q3)〕σz⊗σz-2(q5-q7)σx⊗σx-2(q5+q7)σy⊗σx}
(11)
因此,我们有中心对称态的量子失协可以转化为Χ态的量子失协
Q(ρc)=Q(ρx)
(12)
2 物理解释
考虑各向异性Dzyaloshinsky-Moriya 相互作用XXZ模型。当Dzyaloshinsky向量D为X方向时,双量子比特的哈密顿量为
(13)
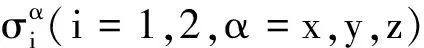
(14)
由(14)知矩阵为中心对称矩阵,注意到,中心对称矩阵的和与积还是中心对称矩阵,因此,相应的吉布斯密度矩阵也是中心对称的。即该模型量子失协是可计算的。
考虑NMR(核磁共振,nuclear magnetic resonance)自旋分子或者原子对量子关联的演化。相应的密度算子为:
(15)
这是一个中心对称矩阵,其中
(16)
这里N为粒子数,a为耦合常数,β为转换温度。文[7]计算了该模型当p=u=0和q=r时的量子失协,应用这个方法执行Hadamard变换,则矩阵有如下Χ态的结构
(17)
写成Bloch形式为:
(18)
对上式施行局域酉变换消除‘xy’交叉项,使得密度矩阵化简为实Χ型。即

(19)
(20)
由Χ态量子失协的计算方法,我们得到Q=min{Q1,Q2}
(21)
这里
(22)
Q2=Sr-S-D1log2D1-D2log2D2,
(23)
(24)
在方程(22)和(23)中,S,Sr分别表示密度矩阵的熵,其中
(25)
这里λj为密度矩阵的本征值
(26)
(27)
考虑如下(PP)态
(28)
这里|Ψ〉为任意2量子比特纯态,I为密度算子,且概率α∈〔0,1〕这个态在(NMR)核磁共振量子计算中作为一个可能的资源,容易验证
〈Ψ|=α(|00〉+|11〉)+b(|01〉+|10〉)
(29)
(|a|2+|b|2=1/2,且{|00〉,|01〉,|10〉,|11〉为计算标准正交基}),这个态ppp满足中心对称态的条件,因此可以利用上面的性质计算量子失协。
3 结论
我们通过局域正交变换建立了中心对称态和Χ型矩阵的联系。由此推出了中心对称态可计算的量子失协计算公式和方法,并且讨论了中心对称态在各种物理系统中的应用。
参考文献:
[1] K.Modi,A.Brodutch,H.Cable,T.Paterik,and V.Vedral.The classical-quantum boundary for correlations;discord and related measures[J].Rev.Mod.Phys,2012,84:1655-1707.
[2] T.Yu and J.H.Eberly.Evolution from Entanglement to Decoherence of Bipartite Mixed “Χ”States[J] .Quantum lnf.Comput,2007,7:459-468.
[3] A.R.P.Rau.Algebraic characterization of Χ-states in quantum information[J].J.Phys.A:Math.Theor,2009,42:0412002.
[4] M.Ali,A.R.P.Rau.and G.Alber.Quantum discord for two-qubit Χ-states[J].Phys.Rev.A,2010,81:042105.
[5] Q.Chen,C.Zhang,S.Yu,X.X.Yi,and C.H.Oh.Quantum discord of two-qubit X-states[J].Phys.Rev.A,2011,84:042313.
[6] Y.-Y.Chen and Y.Zhi.Thermal quantum discord in the anisotropic Heisenberg XXZ model with the Dzyaloshindkii-Moriya interaction[J].Commun.Theor.Phys,2010,54:02536102.
[7] E.B.Fel'dman,E.I.Kuznersova,and M.A.Yurishchev.Quantum correlations in a system of nuclear s=1/2 spins in a srtong magnetic field[J].J.Phys.A:Math.Theor,2012,45:475304.
[8] F.F.Fanchini,T.Werlang,C.A.Brasil,L.G.E.Arrusa,and A.O.Caldeira. Non-Markovian Dynamics of Quanrnm Discord[J].Phys.Rev.A,2010,81:052107.
[9] J.Maziero,R.Auccaise,L.C.C'eleri,D.O.Soares-Pinto,E.R.deAzevedo,T.J.Bonagamba,R.S.Sarthour,I.S.Oliveira,and R.M.Serra.Quantum discord in nuclear magnetic resonance systems at room temperature[J].Braz.J.Phys,2013,43:86-93.
[10] 郭艳芬,等.高职数学教学中的若干策略与方法探析[J].职教论坛,2013(14):49-50.
