脉冲雷达优化设计与资源分配问题
2014-05-11万龙龙邹庆化
万龙龙,邹庆化
(武汉纺织大学 机械与自动化学院,湖北 武汉430073)
在信号探测过程中,脉冲雷达[1]利用发射机对目标进行跟踪测距、方位角、信号接收等操作,该过程对信号作用距离、分辨率、损耗、抗干扰等因素有着很高的要求。因此,需要结合现有资源和成本,对雷达探测资源进行优化组合[2]。本文运用价值工程[3](价值系数等于功能系数比成本系数,强调功能量化)和运筹学中匈牙利算法[4]实现脉冲雷达优化组合,并针对在求解过程需要解决的问题进行讨论,最后实现脉冲雷达优化设计与资源分配。
1 脉冲雷达与其功能最优问题
1.1 脉冲雷达的基本原理
现以典型的单基地脉冲雷达[5]为例来说明雷达测量的基本工作原理,图1示出这种雷达的简化框图。
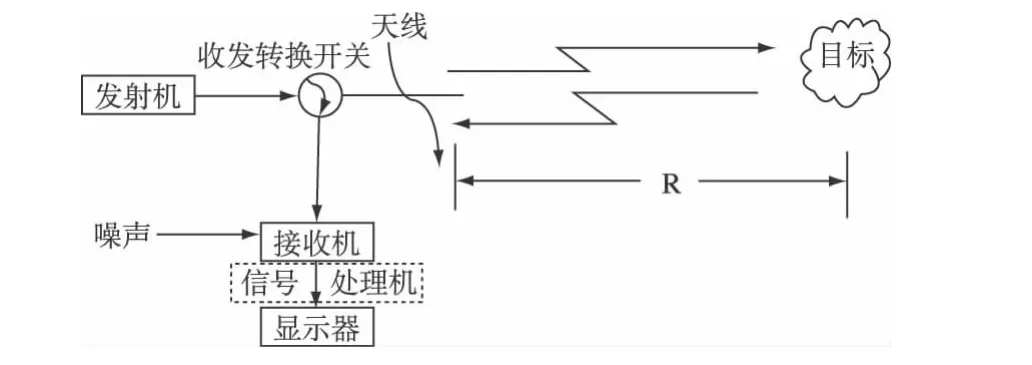
图1 脉冲雷达原理及基本组成
由雷达发射机产生的电磁能,经收发开关后传输给天线,再由天线将此电磁能定向辐射于大气中。电磁能在大气中以光速(约3×108m/s)传播,一部分电磁能被定向天线截获,经传输线收发开关反馈给接收机。接收机将微弱的信号放大并经信号处理送至终端。
1.2 脉冲雷达功能最优问题
能测量目标距离是脉冲雷达的一个突出优点,测距的精度和分辨率与发射信号带宽(或处理后的脉冲宽度)有关。脉冲越窄,性能越好,但是如何既能在保证距离的情况下又能分辨率达到最优?脉冲雷达方案最优决策是基于降低雷达成本,取得产品最佳功能,使其综合工作效率参量达到最大化的一种方法。脉冲雷达方案最优资源分配是以设计具有最大价值(系数)作为标准进行的。价值系数(V)=功能系数(F)/成本系数(C)。即围绕价值标准和功能的分析,以满足本课题的脉冲雷达输出指标为例,其最优设计步骤如下:
(1)制定雷达的设计方案,对方案中的各种功能进行必要的重要性分类和严格功能评分,以使各工艺功能具有确定的功能系数量化值。
(2)对各种方案中的电路成本,进行必要的重要性分类和严格的成本评分,以使其各电路成本具有确定的成本系数量化值。
(3)在单项价值系数最优的设计基础上,优化出综合功能最优设计。
(4)用软件系统,借助VC++系统对脉冲雷达的优化决策进行评定,直观验证了系统的脉冲雷达资源分配方案的最优性。
2 功能重要度系数评定
脉冲雷达工艺路线主要由五个部分组成:信号输入、脉冲法测距、脉冲法测角、匹配滤波(信号处理)和信号输出。目前脉冲雷达的实现技术很多,每一个电路单元可以有多种不同的技术方案,因此有大量的工艺路线组合方案[6]。本研究对象选用一些常用的能够满足从信号输入到信号输出的工艺路线和参量,其雷达工艺路线网络图如图2。

图2 雷达工艺路线网络图
图2中,节点①为发射机,②-④为3种脉冲信号,⑤-⑦为3种测距工艺方案,⑧-⑩为3种测角方案,11-13表示3匹配滤波工艺方案。
就以上的雷达工艺路线网络图可以得到,可供选择的脉冲雷达方案有n=3×3×3×3=81种,因此要对这些方案进行一定的运筹选择,才能根据实际要求选择满足技术和管理上的工艺方案。
首先,要对所有的工艺方案进行对应的量化和重要度的评定。目前评价功能重要性程度有很多种方法,用强制确定法评价出功能的重要度系数就是其中最常用的一种方法[7]。假设图1中的雷达工艺路线要满足雷达输出的作用距离远、分辨率高、抗干扰强、损耗低功能,将其中一种功能依次和其他功能逐一进行比较,相比更重要的功能记为2分,不重要的记为0分,同样重要的记为1分,则各种功能重要度系数的评价过程和结果见表1。

表1 用强制确定法评功能重要度系数
3 单项最优的设计
图2所示的各工艺方案分成不同的子工艺,将这些子工艺列成表2的形式,并逐一对各子工艺的四种功能进行分析,给出其评分和得分。表2集中列出有代表性的子工艺。其分类根据实际情况确定,具体见表2说明。
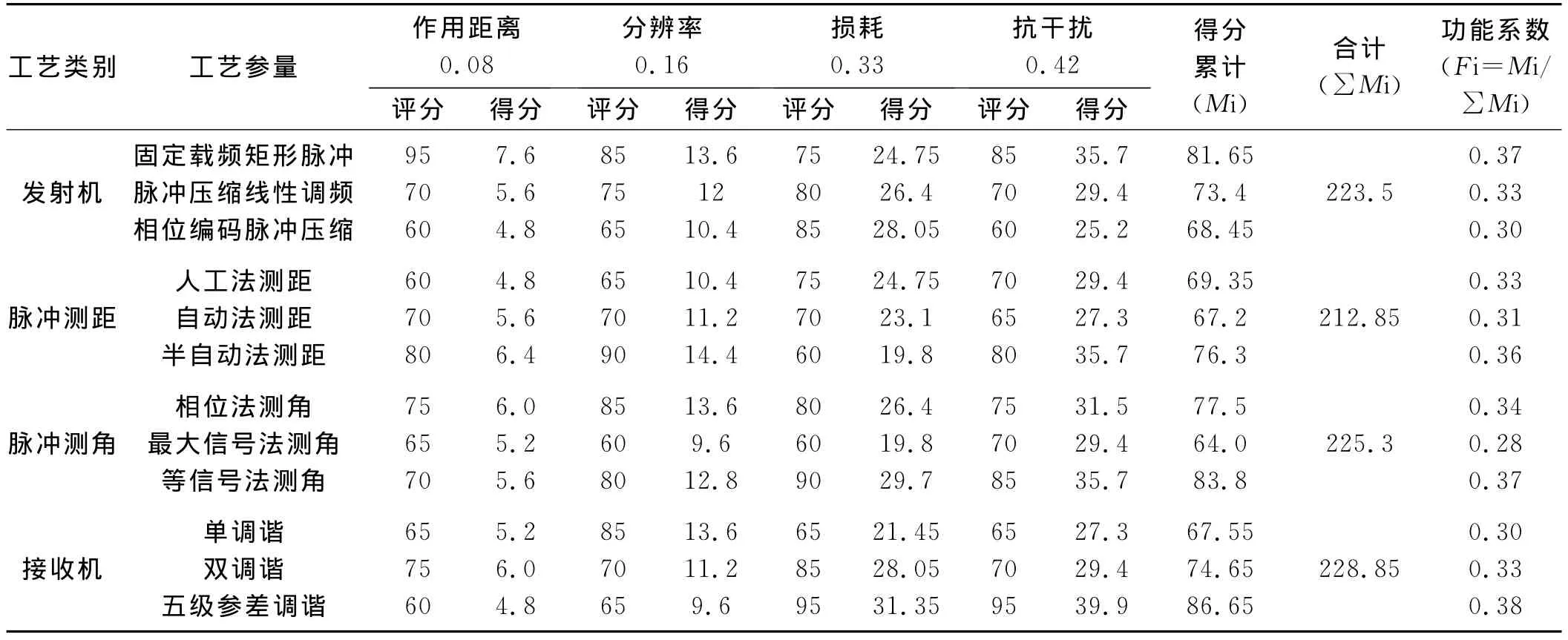
表2 各工艺参量的评分和得分
表2采用百分制直接评分的方法。例如,假如共有4人参与评分,将脉冲压缩线性调频和发射机其它方案比较后该方案的作用距离评分为:(80+65+70+65)/4=70分。
3.1 单项功能最优功能优化分析
在表2中,根据各工艺的功能评分结果,用网络法或表2直接给出的数据分析出单项功能最优工艺。例如用A、B、C、D等表示工艺单项功能最优工艺,则有:
工艺A(作用距离最远):固定载频矩形脉冲—自动法测距—相位法测角—双调谐;工艺B(分辨率最高):固定载频矩形脉冲—自动法测距—相位法测角—单调谐;工艺C(损耗最低):相位编码脉冲压缩—人工法测距—等信号法测角—多级参差调谐;工艺D(抗干扰最强):固定载频矩形脉冲—自动法测距—等信号法测角—五级参差调谐。
以上是图2脉冲雷达资源优化工艺单项功能最佳分析的全过程。
3.2 单项功能最优工艺的成本与价值分析
在求得上述单项功能的最优工艺后,就可以进一步计算出它们的成本和价值系数。假设各个子工艺的成本均由生产费用再加上其他的耗费(按20%生产费用计)组成,在表2的基础上即可得到表3。

表3 各工艺参量的成本与成本系数
表2和表3可以分别查出图2脉冲雷达方案的各子工艺的功能和成本系数,进而可计算出各个子工艺的价值系数,价值系数=功能系数/成本系数[1]。各子工艺的价值系数如表4所示。

表4 各工艺参量的价值系数
最后将表4所示的各子工艺价值系数分别与A、B、C、D四个工艺方案中的子工艺进行相应的配对,就可以得到表5。例如:工艺A(作用距离最远)的价值系数V(A)=0.37/0.35=1.06,于是得到该数值的配对位置应该在该表4中的第一行、第一列处。
由表3和表4知道,工艺A的总价值系数V(A)应由以下部分组成,即V(A)=V(固定载频矩形脉冲)+V(自动法测距)+V(相位法测角)+V(双调谐)=1.06。
工艺B、C、D的总价值系数也同理按照以上的方法求得。选取的角度不同所得到的的单项最优方案也不同,例如作用距离最远,可以选用工艺A,抗干扰最强则选用工艺B。具体情况由实际情况决定。以上就是单项功能最优工艺的成本与价值分析的全过程。这里也充分利用了价值工程理论。
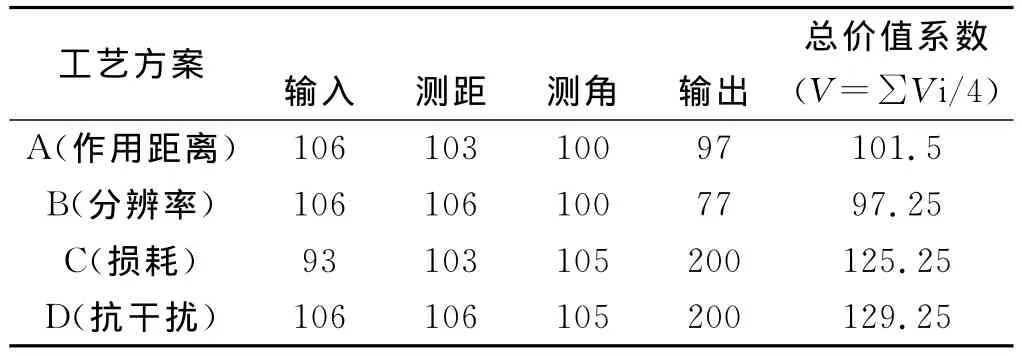
表5 工艺参量单项功能最优工艺及各工艺的价值系数
4 综合指标最优
在实际生产中,往往希望工艺方案各方面的功能都非常好,并不是某一单项功能最优,这就必须要综合考虑已经确定出的全部四种单项功能最优工艺。具体看一看那几个子工艺的价值系数(并非一定是最大系数)加在一起后,能使得所形成的整体工艺方案具有最大的综合价值系数,而这个最大价值系数就是综合功能最优的工艺价值系数,它所对应的工艺即为综合最优工艺[9]。
得到的综合最优工艺价值系数的四种子工艺的价值系数应能满足如下条件:
得到的四种工艺方案中任一种方案,有且只能有一个最佳的子工艺价值系数(不一定是最大)被选出来,并参加方案综合功能最优的工艺价值系数组合。
以上四种工艺方案中选出来的四个最佳的子工艺价值系数,相加起来以后所组成的综合功能最优工艺价值系数须具有最大值。
运筹学理论中解决分配问题的方法可以用来分析上述的两个问题,具体的解决步骤如下:
第一步:将指派问题的系数矩阵变换后,使其在各行各列中都出现0元素。将系数矩阵每一行的元素减去该行最小元素。再将所得到的系数矩阵每一列的元素减去该列最小元素。如果某行(列)已经有0元素,那就无需再减了。
第二步:通过试指派以寻求最优解。步骤如下:
在经过第一步变换以后,系数矩阵中的每行每列元素均已有了0元素;但还需要找出n个独立的0元素。如果能找出,再以这些独立的0元素对应求解矩阵(xij)中的元素为1,而其余元素为0,这便得到最优解。当n比较小时,可以直接用观察法或者是试探法去找出n个独立0元素。如果n比较大时,只能通过一定的步骤去找,如若某行(列)只有一个0元素,则从该行(列)开始,给这个0元素加圈,记为◎。这表示对该行(列)所代表的点,存在一种任务可以指派。然后再划去◎所在行(列)的其它0元素,记作φ。这表示对这行(列)所代表的任务已经指派完,不必再考虑该点了。如果某行(列)只有一个0元素,给该元素加圈,记为◎;然后再划掉◎所在行的0元素,记为φ。
反复进行前面两步,如果所有0元素都被圈出和划掉则停止。
如果仍然有没有划圈的0元素,并且同行(列)0元素至少有两个(表示可以从两项任务中指派其一),这时可采用不同的方案去试探。从余下有0元素最少的行(列)开始,比较这行(列)各0元素所在列(行)中0元素的数目,选择0元素较少的那列(行)的这个0元素加圈(这表示选择性多的要“礼让”选择性少的),将同行同列的其他0元素划掉。该步可反复进行,如果所有0元素都已圈出和划掉则停止。
如果标记◎元素的数目m等于该矩阵的阶数n,即可得到这一指派问题的最优解。如果m<n,则继续转入下一步。
第三步:用最少的直线覆盖所有的0元素,以便确定在该系数矩阵中能够找到最多的独立元素数,步骤如下:
对没有记◎的行打√号;
对已经打√号的行中含φ元素的列均打√号;
对打√号的列中含◎元素的行再打√号;
重复第二、三步直到不能得到新的打√号的行、列为止;
将没有打√号的行画一条横线,对有打√号的列画一条纵线,于是就可以得到覆盖所有0元素的最少直线数。
令这些直线数为l。如果l<n,则说明须再变换当前的系数矩阵,以便能找到n个独立的0元素,若可以则转第四步,否则如果l=n而m<n,则回到第二步(4),另作试探。
第四步:矩阵变换的最终目的是为了增加0元素。为了达到这个目的,先在没有被直线覆盖的部分中找出最小的元素,然后在打√行的各元素中都减去这个最小元素,但将打√列的各元素都加上这个最小元素,保证原来的0元素不变。这样得到一个新的系数矩阵(它的最优解和原矩阵最优解相同)。如果能得到n个独立0元素,则说明已经得到最优解,否则就回到第三步重复进行[10]。
为了计算方便将表5所列的单项功能最优工艺的各项子工艺价值系数扩大100倍使之成为整数形式,再将它们写成价值系数的矩阵(Cij)形式。欲求上述综合功能最优工艺的价值系数,亦即求出Cij的最大分配值。求最大分配值之前,需要对矩阵Cij进行预先处理,即将各矩阵元素用矩阵中的最大值减去自身值,通过这一步的转换就把指派问题求最小值问题转化为求最大值问题。
求解最优解矩阵(Xij)的实际意义为:将某个工艺方案取矩阵(Xij)中每行数字1所对应的子工艺价值系数组合起来,即获得最优综合价值系数(即综合功能最优的工艺价值系数)。子工艺的价值系数分别对应于表5,是由前面具体子工艺的单项最优工艺求解得到的。
所以,综合最优方案的价值系数具体值为:Zmax=(0.93+1.06+1.05+1.03)/4=1.02。
相对应的综合功能的最优工艺方案具体表述为:输入:固定载频矩形脉冲---测距:自动法测距---测角:等信号法测角---匹配滤波:双调谐。
5 结束语
本研究结合价值工程、运筹学、脉冲雷达原理设计了一个小型的脉冲雷达设计工艺参量最优控制的软件,目的是为了解决实际脉冲雷达生产工艺中存在的问题。
本文依托VC++6.0用价值工程和运筹学匈牙利算法实现了脉冲雷达优化资源的分配,得到比较好的分配方案和整体优化效益。脉冲雷达资源优化设计与决策分析是灵活、综合运用雷达原理与实践的重要环节,在具体的脉冲雷达资源分配过程中,必须结合相关的参数与本文所述的方法相结合,以达到具体应用的目的。
[1]沈胜白.价值工程的发展和应用[M].上海:知识出版社,1981.
[2]林同善.运筹学[M].北京:机械工业出版社,1986.
[3]丁鹭飞 ,耿富录.雷达原理[M].西安:西安电子科技大学出版社,2004.
[4]《雷达接收设备》编写组.雷达接收设备(上、下册)[M].北京:国防工业出版社,1979.
[5]M.I.斯科尔尼克主编.雷达手册(第二、三分册)[M].北京:国防工业出版社,1974.
[6]张明友 ,汪学刚.雷达系统[M].北京:电子工业出版社,2005.
[7]邹庆化.金工工艺优化设计[J].机械设计,1996,(7):31-35.
[8]陈 丽,邹庆化.一种低压DC/DC电路的实现[J].机电产品开发与创新,2010,(5):158-160.
[9]Zou Qinghua,ChenLi.Prediction and key computer programming ofmechanical properties of hot rolled plate based on Bp neural network[Z].EI,2009,967-971.
[10]Zou Qinghua,ChenLi.Computer Calculation and plotting on Dynamical Phase Diagrams of Carbon Steel,EI[Z].2009,1055-1064.
