LLC谐振变换器电感电流初值估算
2014-05-11赵升
赵 升
(西南交通大学 电气工程学院,四川 成都610031)
0 引 言
随着效率、功率密度逐渐成为开关电源领域的主要关注点,谐振变换器越来越受到人们的关注[1]。LLC谐振变换器具有原边开关管易实现全负载范围内的ZVS,次级二极管易实现ZCS,谐振电感和变压器易实现磁性元件的集成,以及输入电压范围宽等优点,得到了广泛的应用[2]。
文献[3]采用基波近似法对LLC变换器进行分析。基波近似法是基于一定的近似条件,通过频域分析对LLC变换器进行化简计算,从而获得电压增益等一系列结果。应用基波近似法对LLC变换器进行设计时,由于这种近似计算不可避免的会导致一些误差,不仅给变换器的设计带来一些麻烦,而且无法从理论上对进一步分析LLC谐振变换器的电流控制、前馈控制等控制方式给予准确地数学描述。文献[4]采用时域分析法对LLC变换器进行分析,与基波近似法相比,时域分析法能够准确描述LLC变换器各时刻的工作状态,但文献[4]并未对LLC谐振变换器工作在ZVS区域2[5]的状态进行分析。
本文采用时域分析法,通过求解非线性方程组,推导出LLC谐振变换器工作在ZVS区域2状态下,每周期初始时刻谐振电感电流的表达式。结果表明谐振电感电流初始值与LLC谐振变换器的结构和输出电压有关。与基波近似法相比,所求表达式相对简洁,这不仅为LLC谐振变换器的初期设计提供了帮助,而且对其电流控制、前馈控制提供了一些理论基础。最后,通过搭建160 W的样机验证了理论分析的正确性。
1 LLC谐振变换器工作原理
图1所示为LLC谐振变换器拓扑,谐振电感L、谐振电容C以及励磁电感Lm组成谐振网络。Ug为输入电压,Uo为输出电压,n为变压器的匝数比,R为负载电阻,fs为开关频率,开关周期Ts=1/fs。
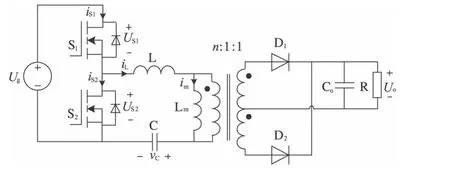
图1 LLC谐振变换器
设LLC变换器的直流增益M为

谐振频率fr为

谐振网络等效阻抗Rac为

由基波近似分析法可以得到LLC谐振变换器的直流增益表达式
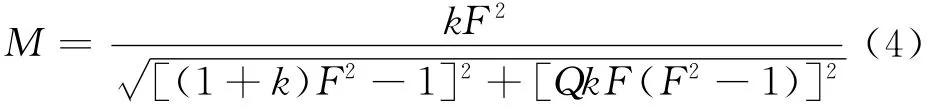
其中
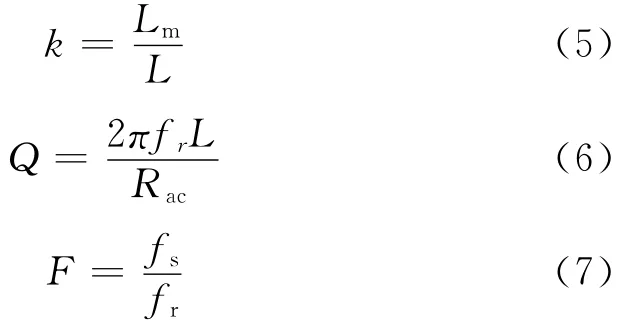
图2所示为L=110μH,Lm=440μH,C=33 nF的电路参数条件下,LLC谐振变换器直流增益M在不同的Q值下随F变化的特性。图2分为三个不同的工作区域,ZCS区域、ZVS区域1和ZVS区域2,分别对应LLC谐振变换器的开关管S1、S2工作在ZCS状态和ZVS状态[5],其中ZVS区域1和ZVS区域2为LLC变换器主要的工作区域。
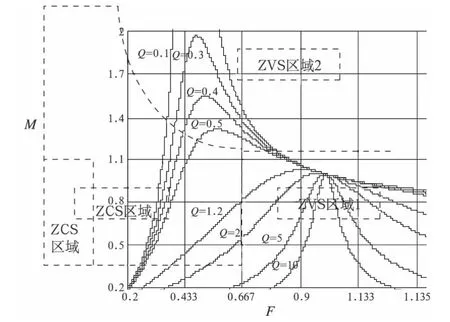
图2 LLC谐振变换器直流增益
图3所示为LLC谐振变换器工作在ZVS区域1和ZVS区域2的波形,其中Us1为开关管S1两端电压,is1为流过开关管S1的电流,iL为流过谐振电感L的电流,im为流过励磁电感的电流,UC为谐振电容C两端的电压,iL(0)为谐振电感电流初值,UC(0)为谐振电容电压初值。文献[4]采用时域分析法列写LLC谐振变换器工作在ZVS区域1的线性方程组,并对电感电流初值iL(0)进行求解,但LLC变换器工作在ZVS区域2为一非线性方程组,文献[4]并未对这一区域进行分析。
2 基于时域分析的电感电流初值估算
为了简化分析过程和结果,需要对一些变量和等式进行归一化。首先定义一些基本量:
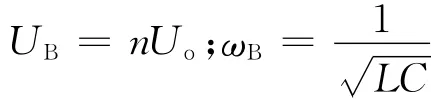
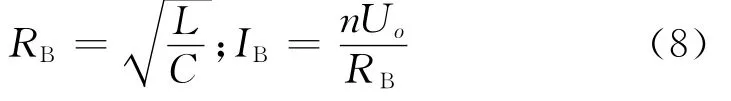

图3 LLC变换器工作波形
定义谐振电感与励磁电感的比值l为

定义归一化开关频率F

定义归一化时间变量θ

定义归一化半周期时长γ
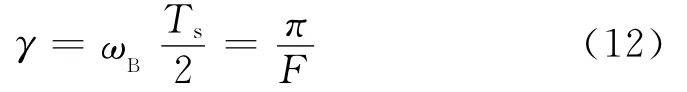
定义归一化电压mx(θ)
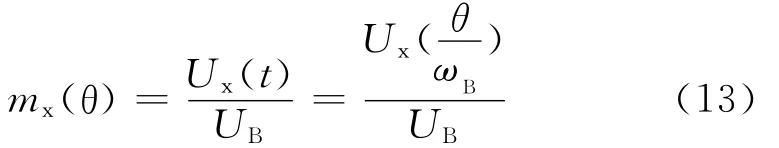
定义归一化电流jx(θ)
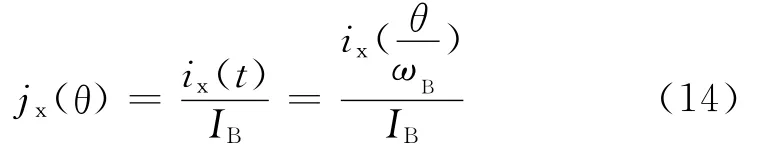
如图4所示为LLC谐振变换器工作在ZVS区域2的归一化谐振电感电流jL(θ)、归一化励磁电感电流jm(θ)以及归一化谐振电容电压 mC(θ)的波形,jL(0)为归一化电感电流初值,mC(0)为归一化电容电压初值,θ1为归一化的时间变量,γ为归一化的半周期时长。LLC谐振变换器工作在稳态时每周期的波形都是对称的[5],因此可仅对半个周期的谐振电感电流、谐振电容电压以及励磁电感电流进行分析。
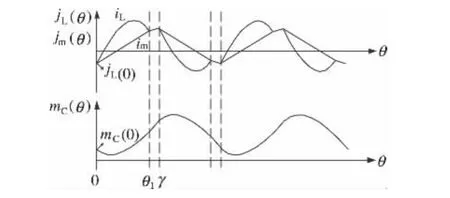
图4 归一化LLC谐振变换器工作波形
由图4分析可知,当LLC谐振变换器工作在0<θ<θ1阶段仅L与C谐振,二极管D1导通、D2关断,励磁电感被输出电压钳位,此时变换器的等效电路如图5所示。
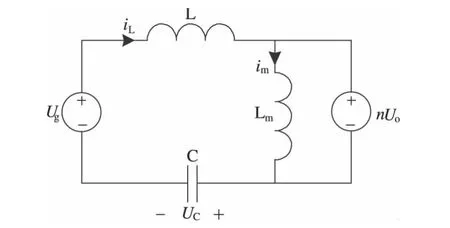
图5 0<θ<θ1阶段等效电路
当LLC谐振变换器工作在θ1<θ<γ阶段,L、C与Lm三者共同谐振,二极管D1、D2均关断,此时变换器的等效电路如图6所示。
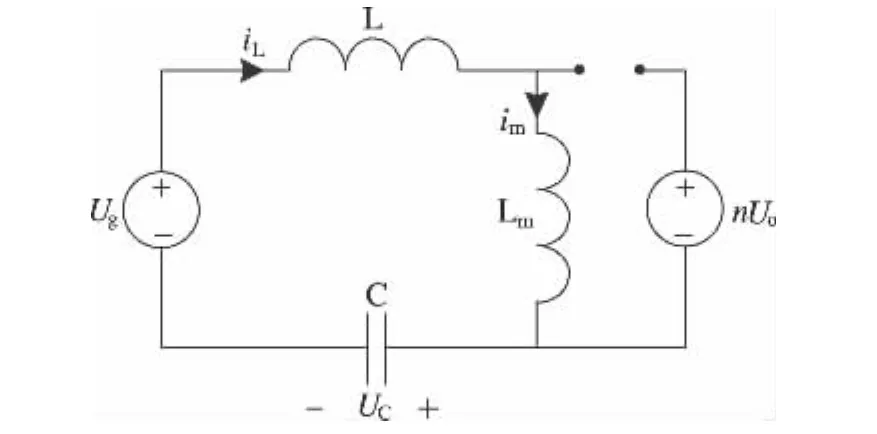
图6 θ1<θ<γ阶段的等效电路
由前述分析可知,θ1<θ<γ阶段为L、C与Lm三者共同谐振,所以列写电路方程会非常复杂,有必要对图6所示的等效电路进行化简。假设L、C与Lm三者的谐振频率远小于L与C的谐振频率,且θ1<θ<γ阶段相对于0<θ<θ1阶段的时长较小,所以可以假设此阶段电感电流值不变。即L与Lm等效为电流源,电流源的值为θ1时刻谐振电感电流值jL(θ1),与电流源串联的电压源Ug可以省略,于是可以得到θ1<θ<γ阶段简化的等效电路,如图7所示。
根据图5所示等效电路列写出0<θ<θ1阶段的时域方程组

图7 工作在θ1<θ<γ阶段简化的等效电路
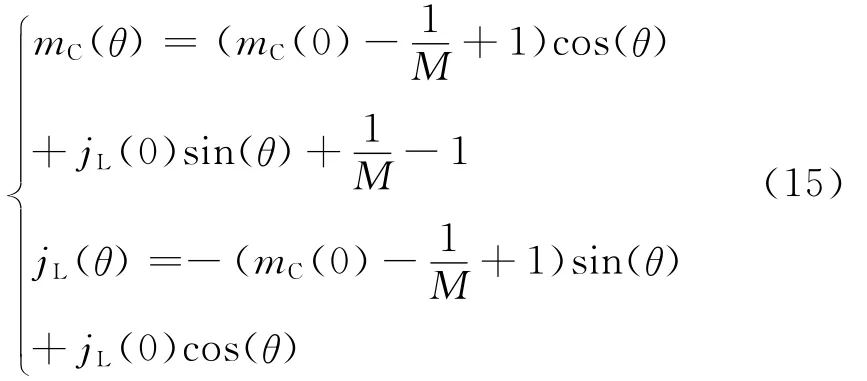
根据图7所示化简的等效电路列写出θ1<θ<γ阶段的时域方程组
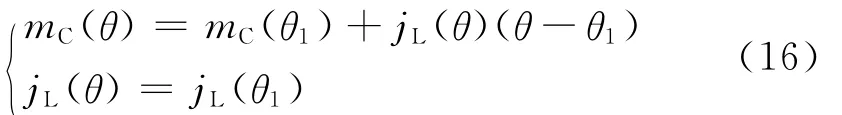
方程组(15)和(16)中,jL(0)、mC(0)、θ1是未知量,M是已知量。
根据励磁电感电流jm(θ)的性质[5]以及前述θ1<θ<γ阶段谐振电感电流不变的假定,可以推导出θ1时刻励磁电感电流的值jm(θ1)
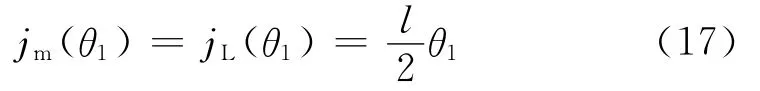
由谐振电感电流和谐振电容电压对称性条件,可以推导出
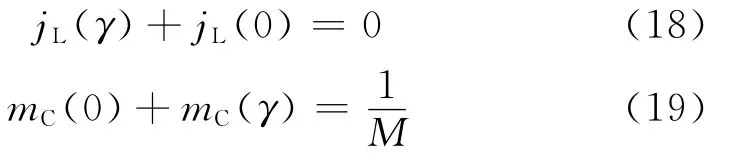
将等式(17)、(18)、(19)代入方程组(15)、(16)中,可以推导出关于未知量θ1的非线性方程
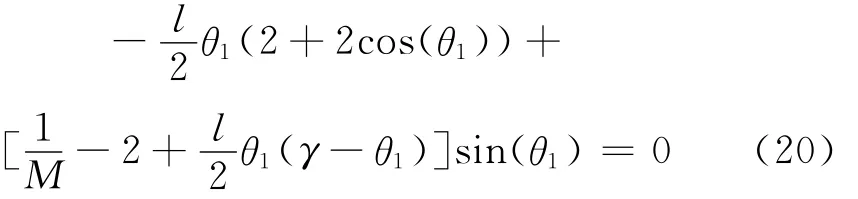
代入不同的已知量M、l、γ,应用迭代法求解非线性方程(20),可以推导出

(注:θ1解的范围为0<θ1<γ,且将π代入非线性方程(20)的左边亦为零)。
将等式(21)代入等式(17)、(18)可推导出归一化的谐振电感电流初值近似表达式

将等式(8)、(14)代入等式(22)可推导出谐振电感电流的初值近似表达式
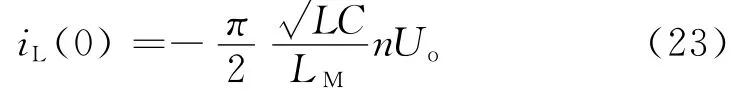
由等式(23)可知LLC谐振变换器工作在ZVS区域2的谐振电感电流初值只与变换器的结构和输出电压有关。
3 仿真及实验验证
为验证理论分析的正确性,本文设计了一个额定输出功率160 W的LLC谐振变换器,其主要参数:L=105μH,Lm=630μH,C=22 nF,n=9,R=3Ω。
假定输出电压Uo=22 V,LLC变换器工作在ZVS区域2状态,根据等式(23),可推导出谐振电感电流的初值iL(0)=-0.741 A。
图8为LLC谐振变换器工作在输入电压为Ug=370 V,开关频率fs=92 kHz,电路参数与前述相同的实验波形。Us1为开关管S1两端电压波形,iL为流过谐振电感电流波形,Uo为输出电压波形。由图可知LLC谐振变换器工作在ZVS区域2,输出电压Uo约为22 V时,谐振电感电流的初值iL(0)约为-0.75 A,与前述理论的计算结果基本相符。
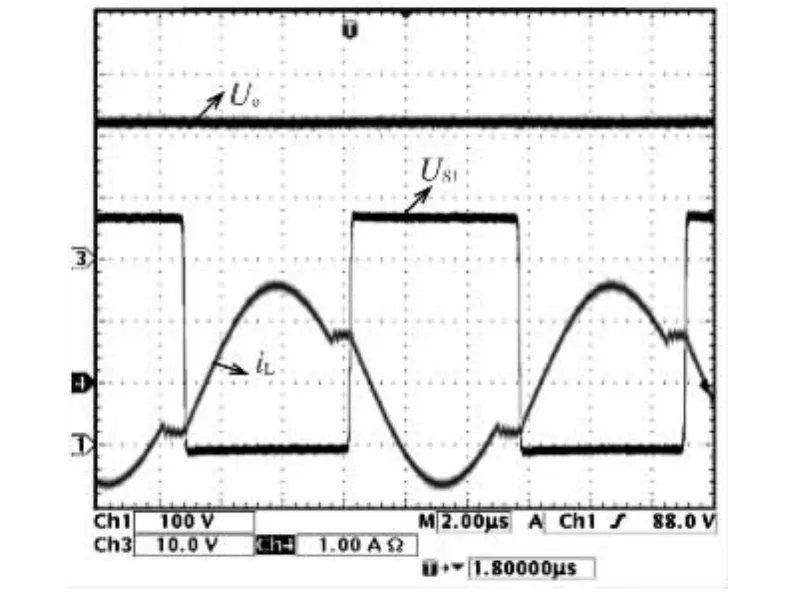
图8 实验波形
4 结 论
本文分析了LLC谐振变换器的工作原理,并采用时域法,通过化简等效电路、求解非线性方程组推导出LLC变换器工作于ZVS区域2的谐振电感电流初值,结果表明谐振电感电流初值大小只与变换器的结构和输出电压Uo有关,并在SABER软件中对工作于ZVS区域2的LLC谐振变换器进行仿真验证,最后实验验证了理论的正确性。
[1]Bo yang,Lee F C,Zhang A J,Guisong Huang.LLC resonant converter for front end DC/DC conversion[C].Applied Power Electronics Conference and Expositon(APEC),2002:1108-1112.
[2]Jee-hoon Jun,Joong-gi Kwon.Theoretical Analysis and Optimal Design of LLC Resonant Converter[C].In the Conference of Power Electronics and Applications,2007:1-10.
[3]Ivensky G,Kats A,Ben-Yaakov S.An RC Load Model of Parallel and Series-Parallel Resonant DC-DC Converters with Capacitive Output Filter[J].IEEE transactions on Power Electronic Systems,2001,14(3):515-521.
[4]Lazar J F,Martinelli R.Steady-State analysis of the LLC Series Resonant Converter[C].Applied Power Electronics Conference and Expositon(APEC),2001:728-735.
[5]Bo Yang.Topology Investigation for Front End DC/DC Power Conversion for Distributed Power System[D].Virgina Blacksburg,VA,2003.
