摆动伺服气缸定位控制策略与实验研究

柏宗春，李小宁

(南京理工大学机械工程学院，江苏南京210094)

0 前言

目前在工业自动化中应用的气动系统主要是顺序动作的控制系统，大多数执行元件只能在始末端定位。随着工业自动化的广泛应用和制造业降低成本，增加利润的需求，人们提出了用低成本的具备行程中任意位置定位功能的气动执行元件代替电气伺服执行元件的新要求。摆动气缸是一种在小于360°范围内作往复摆动转动的气动执行元件，常与气爪，真空吸盘等配合使用用于工件的翻转、夹紧、搬运等作业，工业用途十分广泛。目前工业应用中还主要依靠在其外部设立机械挡块实现定位，本质上仍然是“两点式”的定位方式，无法解决在工业现场中位置不能提前预知的定位问题，且不能实现定位保持，定位刚度仍然较低，基于普通摆动气缸的位置伺服系统在实验室状态下取得良好定位精度也以牺牲气动系统高速特性为代价，且定位刚度低，容易受外界干扰不能实现工业应用。因此研究一种新型的摆动气缸使其依靠自身装置实现在行程中任意位置的快速、高精度定位对于气动技术在位置控制领域的研究有着重要意义［1-5］。

1 摆动伺服气缸结构

气体介质的低阻尼特性实现了气压传动高速特性的同时也是造成气动伺服难以精确控制的原因之一，要想既保持气动系统的高速特性又能实现精确的位置定位，变阻尼力矩控制是实现上述目的的优选途径，因此研究给摆动气动执行器施加主动阻尼，根据运行过程中的不同阶段采取变阻尼的策略满足快速驱动和精确位置定位的双重要求。

作者在对气压驱动和阻尼技术方案进行深入研究的基础上经过反复设计，提出叶片式气压驱动装置、圆盘式磁流变液旋转阻尼器、编码器集成的摆动伺服气缸总体结构方案。图1 为内嵌磁流变阻尼器的摆动伺服气缸结构原理图。

图1 内嵌磁流变阻尼器的摆动伺服气缸

2 摆动伺服气缸控制子系统及定位控制策略

2.1 控制子系统

为了实现摆动伺服气缸在不同工况下的良好定位，需要对驱动气压和阻尼力矩进行协调控制，因此构建了摆动伺服气缸的控制子系统，其组成原理如图2所示。

图2 摆动伺服气缸控制子系统组成原理图

虚线表示系统气动回路，实线表示电回路。由摆动伺服气缸带动负载转台摆动，为了满足应用中不同摆动速度的需求，采用比例流量阀对两腔进排气进行节流控制。用压力传感器测量两腔压力，压力传感器与计数器的输出信号经数据采集卡输入到计算机，计算机输出的控制信号经数据采集卡和阻尼器驱动电源调节阻尼器线圈电流以获得相应阻尼力矩，经数据采集卡和功率放大器驱动比例流量阀以控制摆动伺服气缸两腔的不同节流的进排气。图3 为摆动伺服气缸定位研究实验台照片。

图3 实验台照片

2.2 定位控制策略

2.2.1 阻尼角度

摆动伺服气缸实现即快又准的定位其过程分为小阻尼驱动和大阻尼定位，在摆动伺服气缸运行过程中，通过编码器测量主轴转动角度，当到达目标角度后发出定位信号，关闭进气阀口，磁流变液阻尼器通电工作，此时由于磁流变液阻尼器响应延时以及减速过程固有行程的影响，使得摆动伺服气缸主轴会在设定目标位置之后的位置停止，因此产生超程量，我们称该超程量为阻尼角度。如果可以根据补偿原理，使系统在到达设定位置之前发出定位信号，使补偿量等于阻尼角度就可以大大提高定位精度，因此对定位信号发出后的阻尼角度进行分析。

在阻尼定位过程中主轴所受的力矩如图4所示，设阻尼起始时刻为t0，主轴停止时刻为tm，且起始时刻的系统状态为:角位移θ0、转速ω0、两腔压力p10和p20。

图4 阻尼过程中主轴受力矩示意图

依据运动学原理，在阻尼过程中存在如式(1)描述的运动学关系

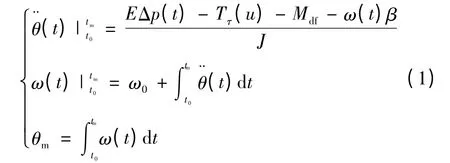
式中:θm为阻尼角度，rad;

E为摆动伺服气缸叶片面积，m2;

Tτ(u)为阻尼器磁致阻尼力矩，N·m;

Mdf为库仑摩擦力矩，N·m;

ω 为角速度，rad/s;

β 为黏性摩擦系数，N·m /(rad/s);

Δp(t)为阻尼定位过程中两腔压力差，Pa;

J为惯性负载，kg·m2。

在定位信号发出后，气缸两腔压力不能立即降为大气压力，两腔均有放气过程，此时两腔压力差形成的力矩仍作用在主轴上，依据气压传动动力学模型［6］，阻尼定位过程中两腔的压力变化可以表示为式(2)的函数形式

则两腔压力差

联立式(1)和式(2)，阻尼角度为变量θ0，ω0，p10，p20，J，u的函数，即

即阻尼角度只与系统状态、转动惯量及阻尼器控制电压有关，但之间的关系涉及高阶微分方程及气体流动模型的求解，函数f很难解析表示，因此要直接解析求出θm是不行的，只能用该公式对阻尼角度的影响因素做定性分析。由于摆动气缸主要用于固定负载的搬运，因此该研究仅针对固定负载下的工况，因此关系式(4)简化为

研究结果表明，BP 型神经网络能够很好地逼近任意连续函数［7］，鉴于神经网络的对非线性函数良好的逼近性能，因此构建了BP 神经网络实现对阻尼角度的预测。

目前关于神经网络结构设计还没有一个统一、完备和确定型的理论框架，一般依据经验或者试凑法对比确立。文中按神经网络结构设计经验［8］确立网络结构，构建基于公式(5)的神经网络非线性模型，确定该网络以p10、p20、ω0、θ0、u为输入，以θm为输出，输入神经元有5 个，隐含层内有11 个神经元，激活函数F1采用logsig 函数，输出层内有1 个神经元，对应的激活函数F2采用purelin 函数，其拓扑结构如图5所示。

图5 用于阻尼角度预测神经网络结构

在系统的工作区域内，选取足够丰富的激励信号作为系统的输入，获取系统的动静态特性。在初始化后，按选取的比例阀电压驱动摆缸转动，当主轴到达设定角度时，发出定位信号，以设定阻尼控制电压u进行阻尼定位，采集阻尼定位起始时刻系统状态参数ω0、θ0、p10、p20，并记录定位信号发出后主轴转动的角度作为阻尼角度θm。重复上述过程，测量多组输入输出数据获得样本数据用来训练神经网络。

2.2.2 阻尼角度动态补偿定位控制策略

在补偿控制原理下，理论上只要依据预测的阻尼角度与当前位置和目标位置的关系确立准确的阻尼起始点达到对阻尼角度的补偿即能实现精确的位置控制，但是阻尼角度的固定补偿方式本质上是阻尼定位过程的开环控制，不能有效地抑制扰动，在实际应用中定位误差较大，研究结合非线性PID 控制策略［9］利用阻尼器输出力矩连续可调的优点实现阻尼角度的动态补偿，以达到良好的控制效果。

在阻尼定位过程中以给定的某参考阻尼控制电压为网络输入，再依据实时状态预测阻尼角度作为阻尼定位过程中的目标模型，通过离目标角度θτ的距离(即剩余行程)与目标模型输出的差值来调节阻尼器控制电压，以使剩余行程与参考阻尼角度一致。

阻尼器控制电压的调节范围为u∈［0，4］V，折中考虑，系统以uref=2 V 作为神经网络预测参考阻尼角度的控制电压输入，即

其中，非线性映射f即为训练好的神经网络。

基于阻尼角度动态补偿定位控制策略的摆动伺服气缸定位系统控制框图如图6所示。

图6 阻尼角度动态补偿的定位控制策略

摆动伺服气缸定位系统的运行过程如下:

(1)气压驱动

根据实际运行速度要求，选取合理比例阀驱动电压对摆动伺服气缸气压驱动。需要说明的是，选取越大的比例阀驱动电压可以实现更快的气压驱动速度，但由于气缸启动行程和阻尼行程的固有存在，对于在较小行程下的定位，对比例阀驱动电压的选择不宜过大，对比例阀最大驱动电压vmax的选取可以通过实验确定。

(2)运行阶段切换

在气压驱动阶段，在每个运行周期采集系统的状态参数，根据阻尼角度的预测结果，当θτ-θ ≥θref时进入阻尼定位阶段。

(3)阻尼定位控制

在系统进入阻尼定位后，外界任何有界的扰动都反映在系统的状态参数上，神经网络依据实时状态参数更新当前工况下的阻尼角度，对剩余行程与当前工况下的网络预测的阻尼角度进行比较，依据差值利用非线性PID 控制器对阻尼器的控制电压进行调整，可表示为

阻尼器控制电压为

(4)定位保持

为了提高系统的定位刚度，防止系统定位后扰动造成主轴的偏移，在定位完成后给阻尼器一控制电压对主轴起到定位保持作用，定位保持电压的值根据扰动量界确定。

3 实验研究

为了检验摆动伺服气缸试验样机的性能，对摆动伺服气缸样机进行了试验，检验其在提出的阻尼角度动态补偿定位控制策略下在行程中任意位置的定位效果。

3.1 阻尼动态过程

摆动伺服气缸完成一次位置定位分为驱动阶段和阻尼阶段，其中驱动阶段仅根据工况进行开关控制，对主动阻尼的控制是实现快速、精确定位的关键，图7 为在控制器比例系数kp为14 V/rad 下阻尼定位过程中摆动伺服气缸内部状态的动态过程，包括参考阻尼角度、系统剩余行程、速度及控制信号。

图7 摆动伺服气缸阻尼定位动态过程

由图7 可以看出，摆动伺服气缸在阻尼定位过程中，速度无突变平滑下降，通过非线性PID 控制器调节阻尼控制电压，剩余行程能较好地跟踪神经网络的预测阻尼角度，获得较高定位精度。

3.2 多点定位

在供气压力0.42 MPa，比例阀驱动电压v=3.2 V，目标定位点为:40°—140°—240°—140°—40°下，图8 为多点定位实验曲线，由图可以看出，对于不同的设定位置都可以达到良好的控制效果，稳态误差在±1.0°范围内，无超调和震荡，调节时间小于0.5 s。在定位完成后给阻尼器施加一定的保持电压，产生的阻尼力矩能够有效地抑制了在普通气动伺服中出现的黏滑震荡及漂移现象，较大地提高了定位刚度。

图8 多点定位实验曲线

3.3 定位精度和时间

表1 列出了部分工况下，摆动伺服气缸在阻尼角度动态补偿定位控制策略下的定位误差和定位时间。

摆动伺服气缸完成一次运行的时间包含驱动运行时间和阻尼定位时间，驱动阶段运行时间受行程、气源压力、比例阀驱动电压等影响。由表1 可以看出，阻尼定位阶段时间都在150 ms 以内，以比例阀驱动电压v=3.34 V，气源压力0.45 MPa，目标位置θτ=180°为例，摆动伺服气缸完成一次运行定位的总时间为0.45 s，保持了气动系统高速特性。配合提出的控制策略，摆动伺服气缸的定位精度均在±1.0°范围内。

表1 定位误差和定位时间

4 结论

(1)构建了摆动伺服气缸控制子系统，对摆动伺服气缸控制特性进行了理论分析，得到了阻尼角度与状态变量之间的非解析函数关系，并利用神经网络对该函数关系进行逼近。

(2)针对阻尼角度固定补偿下开环控制精度差的缺点，采用非线性PID 控制器调节阻尼器控制电压，以实现阻尼定位过程中的闭环控制，提出阻尼角度动态补偿的定位控制策略。

(3)在阻尼角度动态补偿的定位控制策略下摆动伺服气缸既保持气压传动高速特性又实现行程范围内任意位置的快速、精确定位，实验表明阻尼定位时间都在150 ms 以内，且过程平稳无速度突变，实际位移无超调和震荡，定位误差在±1.0°以内，表明在快速驱动与精确定位方面取得了较大的进展，具有良好的应用前景。在研究的基础上，对所研发的摆动伺服气缸申请了国家发明专利并获得授权，专利号为201010211192.2。

［1］路甬祥，阮健，陈行.气动技术的发展方向［J］.气压与气动，1991(2):2-3.

［2］李小宁.气动技术发展的趋势［J］.机械制造与自动化，2003(2):1-4.

［3］Technology:Current Practice and New Developments［J］.IEE Colloquium，1996(2):311-316.

［4］王祖温，杨庆俊.气压位置控制系统研究现状及展望［J］.机械工程学报，2003(12):10-16.

［5］陈启复.对我国气动工业现状与未来发展的思考——气动行业“十二五”发展规划建议［J］.液压气动与密封，2012(1):16-22.

［6］李建藩.气压传动系统动力学［M］.广州:华南理工大学出版社，1991.

［7］Sandhya Samarasinghe.神经网络在应用科学和工程中的应用——从基本原理到复杂的模式识别［M］.史晓霞，等译.北京:机械工业出版社，2010.

［8］MATLAB 中文论坛.MATLAB 神经网络30 个案例分析［M］.北京:北京航空航天大学出版社，2010.

［9］郭彦青，姚竹亭，王楠.非线性PID 控制器研究［J］.中北大学学报，2006，27(5):423-425.