UCM流体的最小二乘有限元解法

周少玲

(河北工程大学 理学院，河北 邯郸 056038)

非牛顿流体力学是一门新兴的学科，它起源于高聚物加工的需要，涉及广泛的工业领域，是力学、现代数学、化学和各工程科学的交叉与综合，特别是与材料科学有着十分密切的联系[1-3]。它是现代流体力学的重要分支，也是现代流变学的重要组成部分。近几十年来，由于人们认识到一些复杂的流体(例如聚合物溶液、血液、油漆等等)不能用Navier-Stokes方程来描述，因此对非牛顿流体模型方程的研究越来越受到学者们的重视[4]。非牛顿流体的运动方程要比Navier-Stokes方程阶数更高，并且具有更强的非线性性质。UCM模型[5]能够很好地描述某些二阶流体(例如具有高Deborah数的弹性流体)的流变特征，本文主要讨论该模型的数值解法。

1 预备知识

设Hs(Ω)(s≥0)为Soblev空间，其内积和范数分别为(.,.)和‖ · ‖s。当s=0时，Hs(Ω)空间即为L2(Ω)空间，相应的范数、内积分别为(.,.)和‖ · ‖。引入下面两个函数空间

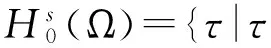
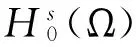
(1)

2 本构方程线性化

考虑稳定的不可压缩UCM蠕动流体

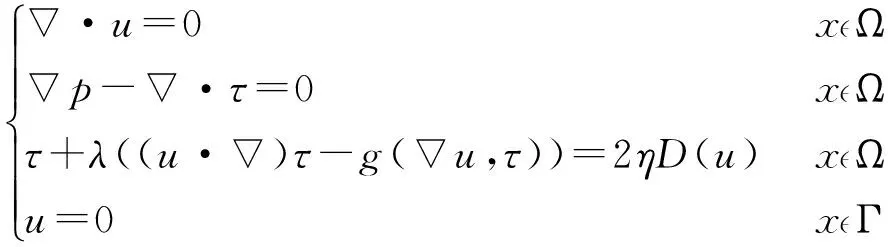
(2)

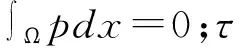
首先引入下面的函数空间

V={v|vH1(Ω)d,v|Γ=0}

Q={q|q

Ts={τ|τL2(Ω)d×d,τij=τji}

T={τ|τTs,‖u1·τ‖<∞}

这里u1是速度u的近似值，L2(Ω)d×d是由d×d维矩阵函数构成的空间，且矩阵中每个元素都是平方可积的，记Φ=V×Q×T。

由于UCM流体的本构方程(即(2)中的第3个方程)是非线性的，所以其数值求解比较困难，考虑将本构方程进行线性化处理。设τ1为τ的近似值，且u1和τ1满足

(3)

max{ ‖u1‖∞, ‖u1‖∞, ‖τ1‖∞, ‖τ1‖∞}≤M<∞

(4)

对本构方程中的非线性项进行线性化近似

u·τ≈u1·τ+u·τ1-u1·τ1

(5)

g(u,τ)≈g(u1,τ)+g(u,τ1)-g(u,τ1)

(6)

非线性问题(2)转化为

(7)

其中B(u,τ)=λ(u·τ1-g(u1,τ)-g(u,τ1),F=λ(u1·τ1-g(u1,τ1)。定义如下的最小二乘泛函

J(u,p,τ;F)=‖p-·u‖2+‖τ+λ(u1·τ)+B(u,τ)-2ηD(u)-F‖2

(8)

对于(u,p,τ)，给出下面的范数

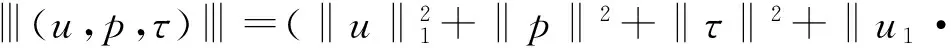
(9)

定理1 假设(u,p,τ)Φ，则存在正的常数c和C，使得对于足够小的M和λ有

c‖ |(u,p,τ)| ‖≤J(u,p,τ;0)≤C‖ |(u,p,τ)| ‖

(10)

证明：显然，右面的不等式可以由范数的三角不等式和 (4) 式推导出来，下面只需证明左边的不等式。记

H=‖p-·u‖2+‖τ+

λ(u1·τ)+B(u,τ)-2ηD(u)‖2

任取φ由格林公式和柯西-施瓦兹不等式得

设φ≠0，则

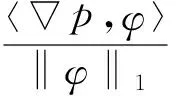
由H-1(Ω)空间范数的定义，得

(11)

根据文献[6]中的引理2.1，有‖p‖0≤

C‖p‖-1成立，得到下面的不等式

‖p‖0≤C(‖p-·τ‖-1+‖τ‖)≤

(12)

利用文献[7]中的定理2.1，可得

‖u‖1≤C1‖u‖≤C2‖D(u)‖

(13)

‖u·τ‖≤

(14)

‖D(u)‖2+‖τ‖2≤CH

(15)

J(u,p,τ;0)≥‖p-τ)-2ηD(u)‖2-‖B(u,τ)‖2≥p-·u‖2+‖τ+

λ(u1·τ)-2ηD(u)‖2)-‖B(u,τ)‖2=

又因为

‖B(u,τ)2=λ‖u·τ1-g(u1,τ)-g(u,τ1)‖2≤λ(‖u·τ1‖2+‖g(u1,τ)‖2+

‖g(u,τ1‖2)≤CM2λ(‖u‖2+‖τ‖2+

得到

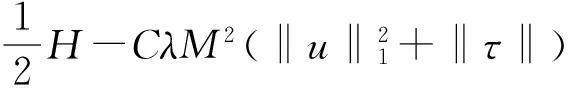
C‖ |(u,p,τ)| ‖ 证毕

3 有限元求解

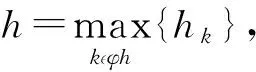
上面的定理证明了泛函J(u,p,τ;0)的椭圆性，但是因为其中包含了范数‖·‖-1，所以并不实用。考虑将范数‖·‖-1用‖·‖代替，但对于各项需要乘以适当的权。建立如下新的泛函

Jh(u,p,τ;F)=‖p-·τ‖2+h-2

2ηD(u)-F‖2

(16)

问题的求解就转化为最小二乘问题：求(u,p,τ)Φh，使得

(17)

将式(16)记为

Jh(v,q,σ;F)=‖L1(σ,q)‖2+

h-2‖L2(v)‖2+h-2‖L3(σ,v)-F‖2

(18)

4 结语

UCM流体模型能够较好地描述一类非牛顿流体，但是由于其非线性的特点，其数值求解往往比较困难。本文在算子水平将非线性项线性化，并使用最小二乘有限元方法和迭代方法求解，算法的实用性较强。

参考文献：

[1] HOU L, NASSEHI V. Evaluation of stress affects flow in rubber mixing[J]. Nonlinear Analysis, 2001, 47(3): 1809-1820.

[2] HOU L, CAI L. Nonlinear property of the visco-elastic-plastic material in the impact problem[J]. Journal of Shanghai University: English Edition, 2009, 13(1): 23-28.

[3] 李本军,来永伟.Q-S曲线判定及问题探讨[J].中国煤炭地质,2012,24(9):41-43.

[4] ABBAS Z, SAJID M, HAYAT T. MHD boundary-layer flow of an upper-convected Maxwell fluid in a porous channel[J]. Theoretical and Computational Fluid Dynamics, 2006(20): 229-238.

[5] 林 群， 严宁宁. 关于Maxwell方程混合元方法的超收敛[J]. 工程数学学报, 1996, 13(12): 1-10.

[6] CAI Z, MANTEUFEEL T A, MCCORMIC S F. First-order system least-squares for velocity-vorticity-pressure form of the Stokes equations, with application to linear elastically[J]. Electronic Transactions on Numerical Analysis, 1995( 3)：150-159.

[7] CAI Z, WESTPHAL C R. An adaptive mixed least-squares finite element method for viscoelastic fluids of Oldroyd type[J]. Journal of Non-Newtonian fluid mechanics，2009(159)： 72-80.

[8] 杨 春. 基于最小二乘支持向量机岩土本构模型的有限元分析[J]. 河北工程大学学报: 自然科学版, 2013, 30(3)： 26-29.