基于SWMM的节制闸影响研究

2014-05-10姜新佩

河北工程大学学报(自然科学版) 2014年1期

李晨，姜新佩

(河北工程大学水电学院，河北邯郸 056038)

南水北调中线工程是一个特大型跨流域调水工程，从丹江口水库引水，沿唐白河平原及黄淮海平原西部跨江、淮、黄、海四大流域，自流输水到北京、天津、输水线路全长约1 432 km，总干渠以明渠输水为主，北京、天津段采用涵管输水。总干渠输水由61个节制闸控制,沿线布置有分水口门90个,退水闸51个。主要供水目标为京、津、华北地区，供水范围分属京、津、冀、豫、鄂5省市[1]。

中线调水工程调水量沿线变化不均匀，自然状态下的水流无法满足输水要求。无论渠道流量大或小，都保持渠道水位在一定的范围内，也只能通过节制闸来实现。节制闸是实现渠道系统控制的重要建筑物。为了实现对渠道水位和流量的调控，渠道系统中必须设足够多的节制闸，节制闸使渠道保持较高水位，有利于保护渠道衬砌安全[2]，本文对闸门启闭时间和节制闸的不同开度引起的水位波动的影响进行了研究，采用SWMM模型模拟，给出不同闸门开度变幅下对水位变动的影响。

1 数学模型

SWMM[3](Storm Water Management Model)是一个动态的降水-径流模型，可以对研究区域输入的数据进行编辑、模拟水文、水力和水质情况。其水力学模块除了能模拟自然河道中的水流，还可以模拟各种形状的封闭管道和明渠管道中的水流。

SWMM模型中水力学模块中描述非恒定流的基本控制方程为圣维南方程组，由动量方程和运动方程构成。

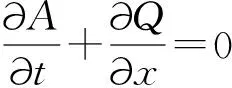
(1)

(2)

SWMM模型通过结点把管道或渠段连接在一起进行水力求解分析，结点处水头求解表达式为

(3)

式中Astore—节点表面积；ΣAs—连接节点的管段中水的表面积；ΣQ—节点的入流总和。

SWMM模型求解方程(1)(2)(3)把他们转换成显示的有限差分公式集，由已知t时刻的值来计算t+Δt时刻管段流量和节点水深。流量公式如下

(4)

水头计算公式为

(5)

式中△Vol-通过结点的净流量体积；ΔVol=0.5[(ΣQ)t+(ΣQ)t+Δt]Δt。

SWMM模型对方程(4)(5)采用欧拉修正算法求解，方程(4)用时刻t的值求解下一时间步长t+△t的渠段流量，同理方程(5)求解结点水头值。

2 算例及结果分析

假设渠道首尾水位恒定，其中任一渠段的闸门开度改变时，渠道将从恒定流转变为非恒定流。渠道的非恒定流特性用圣维南方程组描述。

取简单模型，每个渠段类似小水库，选取其中某一渠段，渠段首尾设有节制闸进行调节，如图1，渠段长度25 000 m，横截面为梯形，底宽b为7 m，边坡系数m=20，纵坡i=1/25 000，糙率n=0.015。初始条件为闸门调节前初始状态计算节点处流量和水位的初始值。可根据初始流量及水流条件，通过恒定流水面线计算得出。渠中为均匀流时，上游闸门开度为2.5 m。不同工况采取不同闸门调控，计算各断面在瞬变过程中各时刻的水深、流量等水力参数。

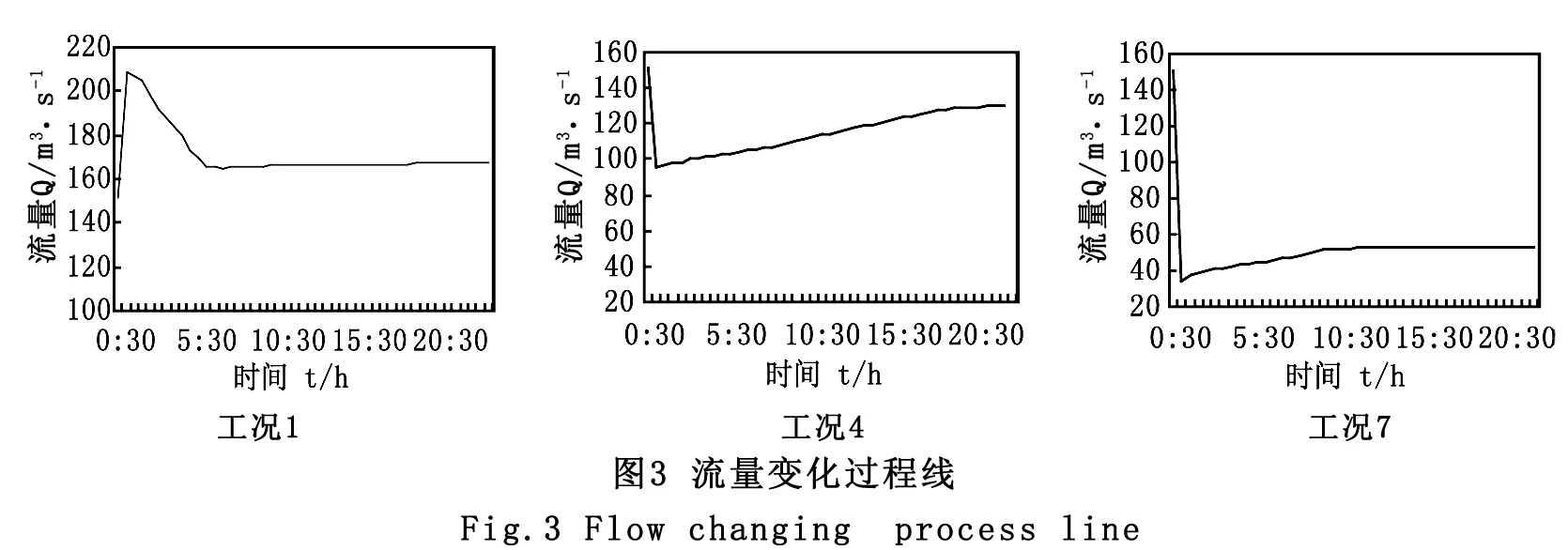
本次计算模拟工况为闸前正常水位运行方式[4]下研究闸门调节速度和闸门开度变幅，研究了9种计算工况如表1，表1中闸门开度变化幅度正为增加，反之减小。工况1、工况4、工况7模拟结果如图2和图3。

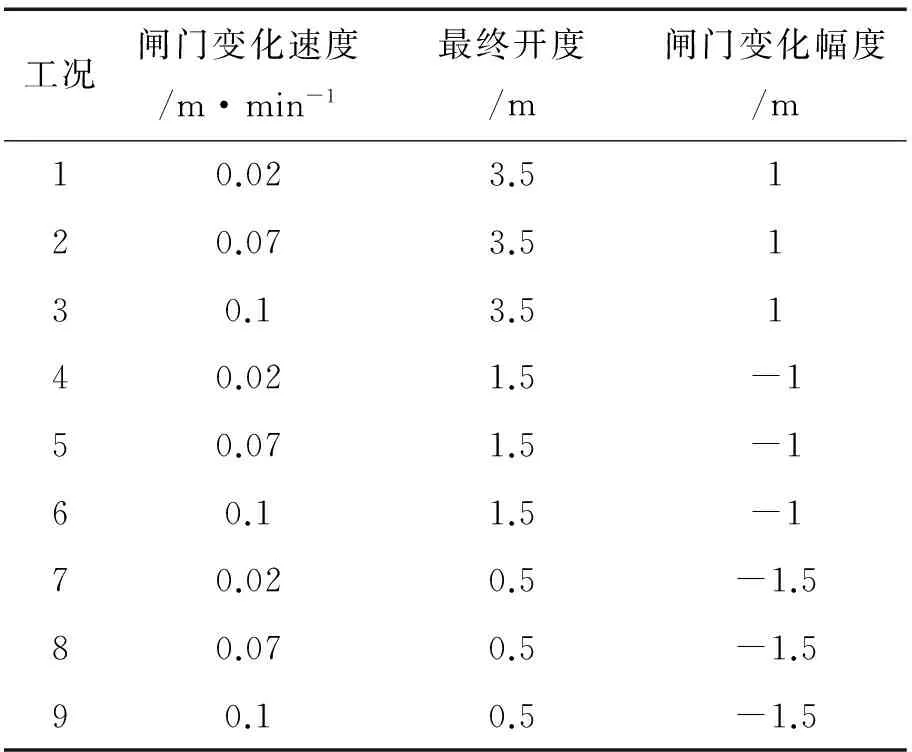
表1 节制闸开度变化模拟工况

图2是闸后水位变化过程线，图3是闸下流量过程线。由上图可知:闸门开度增大或减小，闸门调节完后，闸后水位和闸下出流量过程线有明显的转折点；转折点以后的曲线形态都有所改变，或者按原来趋势变化，或者按相反趋势变化，因为转折点前主要是由闸门调节产生的干扰波所引起，闸门调节完以后(即转折点后)水位及流量的变化主要是由渠道自身调节最终趋于稳定；由三种工况图对比可得闸门开度变化幅度越大，水位波动影响越明显，对渠道的衬砌安全也越不利。

闸门的不同调节速度(闸门开度相同)变化规律[5]，如图4、5。

开始一个时段，闸门调节速度越快，流量和水位变化也越快，此时段之后，各过程线变化幅度取决于闸门开度变化，跟闸门调节速度无关。不同闸门调节速度对水位波动影响符合丁志良研究结果[6]：闸门调节速度越大时，流量及水位的变率也越大，水位也越早出现波动情况，对渠道的衬砌安全也越不利，但是渠道的响应时间会缩短，且最终都能过渡到相同的平衡状态。