鄂东气田韩城矿区煤层横波时差测井曲线的构建方法

杨秀春, 张继坤, 周科

(中国石油煤层气有限责任公司, 北京 100028)

0 引 言

横波也称剪切波,其质点振动的方向与传播的方向垂直[1]。以前在硬地层测井中用长源距声波获取声波,但在像煤层这样的软地层需要进行偶极子横波测井[2],如5700测井系列的MAC。偶极子横波测井是专门针对软地层而设计的一种获得横波信息的测井方法[3]。研究区煤层气井中,大多数井尚没有进行多极阵列声波测井,因而无法获得横波测井资料,这给岩石力学参数计算及压裂高度预测带来不便[2]。现有横波时差估算方法研究成果集中在常规砂泥岩地层[4-6],针对煤储层的横波时差构建方法尚不多见。由于煤储层地质条件、声学特性与常规砂泥岩地层截然不同,现有的横波时差计算方法是否能够移植到煤储层上,需要开展研究工作佐证。本文在吸收借鉴常规砂泥岩地层横波时差估算方法的基础上,充分挖掘与煤岩地层横波时差测井曲线较为敏感的测井参数,给出3种方法构建煤层的横波时差计算模型,开展实例计算分析,优选出适合于煤层的横波时差曲线构造方法。

1 基于常规测井资料构造横波时差

1.1 经验公式法

不同的岩石,其纵横波时差不同[7],对于某一固定的岩石其骨架声波时差值是一定的,而且对某一特性的流体其声波时差值也是固定的[8]。根据不同的岩石,经验公式为

(1)

式中,Δts为拟合的横波时差,μs/m;Δtc为纵波时差,μs/m;Δtmas、Δtmac分别为地层骨架的横波时差与纵波时差,μs/m;Δtfs、Δtfc分别为地层流体的横波时差与纵波时差,μs/m。

1.2 利用纵波和密度测井资料拟合横波时差

已有研究表明[9-11],砂泥岩的横波时差与纵波时差、密度测井都有较好的相关性。本文为了揭示煤岩的纵横波时差及密度测井之间内在相关性,利用测有横波时差的井作了煤岩扩径等环境影响校正,提取了煤岩段纵横波时差和密度测井数据,采用数理统计分析技术构建了图1、图2所示的横波时差与纵波、密度测井的交会图。由此交会图易知,煤岩的纵波时差、密度与横波时差均具有较好的相关性。本文拟采用纵波时差、密度构建2个测井参数的横波时差拟合方程。

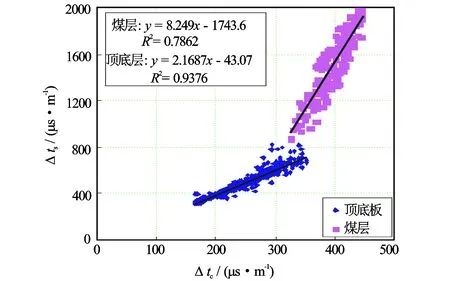
图1 纵波时差—横波时差交会图

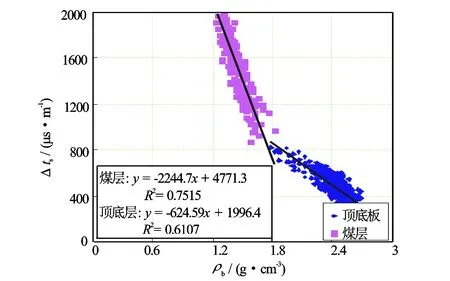
图2 密度—横波时差交会图

煤田测井长期经验认为[5],煤岩的横波时差与纵波时差、密度测井存在非线性关系

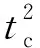
(2)

式中,ρb为密度测井值,g/cm3;x、y、z为拟合系数。

本文采用多元线性拟合和多元非线性拟合对纵波时差、密度及横波时差进行了拟合,构建了横波时差测井解释模型(见表1)。

表1 煤岩横波时差测井解释模型

利用该拟合方程对横波时差进行了误差检验分析。表2是利用表1所示方程拟合的煤层横波时差的部分误差分析数据。采用多元线性公式(方程1)计算的横波时差相对误差介于0.37～12.04,平均相对误差3.17。利用多元非线性公式(方程2)拟合计算的横波时差相对误差介于0.07～10.39,平均相对误差1.26。从2个回归方程的检验结果可知,方程2计算精度较方程1高,因此在实际生产中建议使用非线性拟合方程模型。

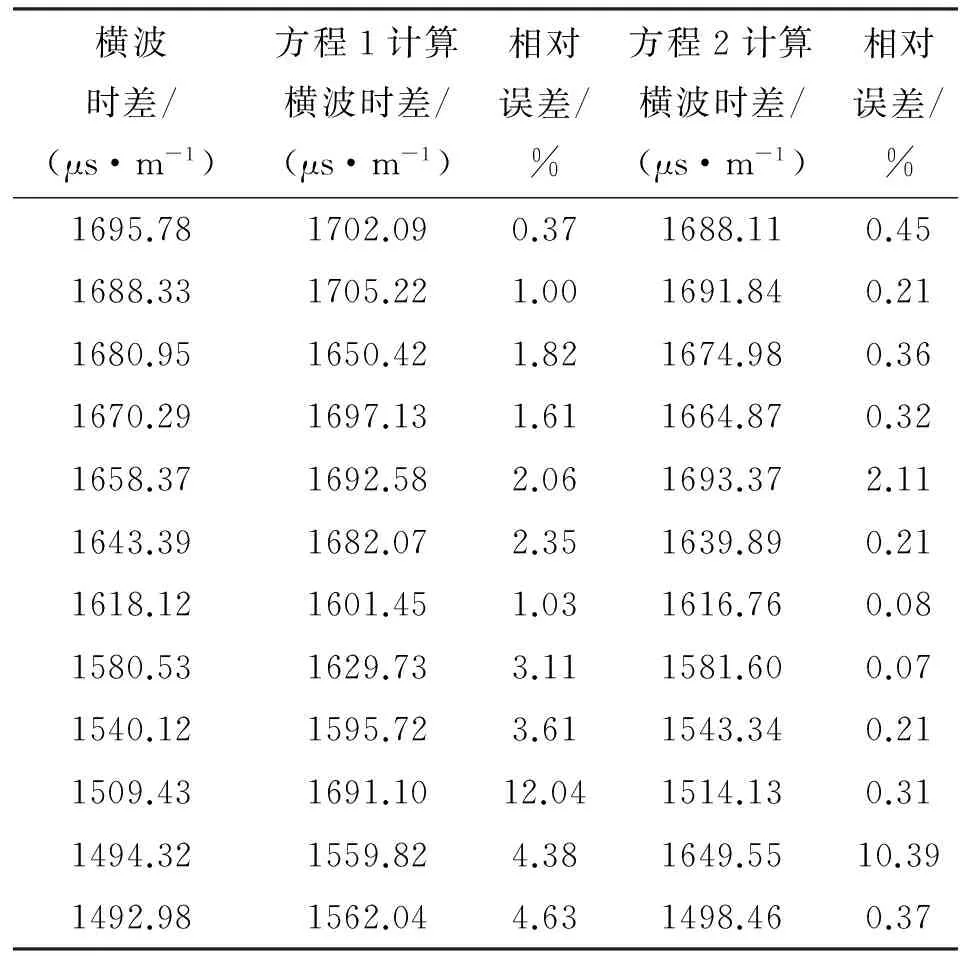
表2 煤层横波时差计算结果误差分析数据表

2 基于岩性指示曲线构造横波时差

2.1 理论基础

研究地下岩石速度的模型有很多,其中Biot-Gassman较为经典,其数学表达式为[12]

(3)

(4)

式中,vP、vs分别为纵波速度和横波速度,m/s;ρc为干岩石骨架体积模量,g/cm3;Ks、Kf分别为固体矿物和流体体积模量,GPa;φ为岩石孔隙度,小数;Kd、μd分别为干岩石骨架体积模量和剪切模量,GPa。

由式(4)可见,求取纵、横波速度的关键在于对岩石骨架弹性模量的准确计算,即获取不同岩石类型、不同流体性质条件下的岩石有效弹性模量,其Biot-Gassman可改写为

(5)

式中,Ke为岩石等效体积模量,GPa。

通常,φ-Ks/Kf远远大于1-φ-Kd/Ks,因此可忽略1-φ-Kd/Ks,式(5)可简化为

Ke=Kd+(Kf/φ)(1-Kd/Ks)2

(6)

式(6)中第1项反映了岩石骨架的影响,第2项反映了孔隙流体的影响。当一个地区孔隙度相差不大且岩性相对致密时,横波时差主要受岩性的影响,由此,为建立以岩性变化特征为基础的横波时差计算模型奠定了理论基础。

2.2 建立岩性指示曲线

通过系统分析研究发现,研究区煤岩地层中,中子、密度及电阻率测井曲线对岩性较为敏感。本文利用这3条曲线之间的关系构建岩性指示曲线[13-14]Lc,其数学表达式为

(7)

该指示曲线反映了岩性的相对变化,CNL、ρb、Rt分别为补偿中子、补偿密度和深电阻率测井响应值。

2.3 建立横波时差拟合公式

研究偶极声波资料井提取的横波时差测井数据发现,该区横波时差与岩性指示曲线具有较好的相关性,据此建立基于岩性变化的横波时差拟合模型

Δts=1300.3·e3E-06·Lc

(8)

式中,Δts为拟合的横波时差值(见图3)。

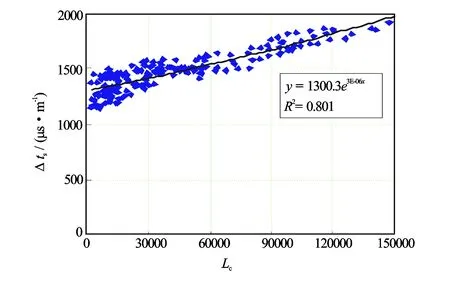
图3 岩性指示曲线与横波时差关系图

2.4 误差分析

利用横波时差拟合公式(8)进行煤岩的横波时差计算,取得了较为满意的效果(见表3)。该模型构建简单,具有较强的实用性和针对性,便于现场操作和应用。在实际应用时,应对测井曲线进行环境校正处理,以期提高横波时差拟合精度。

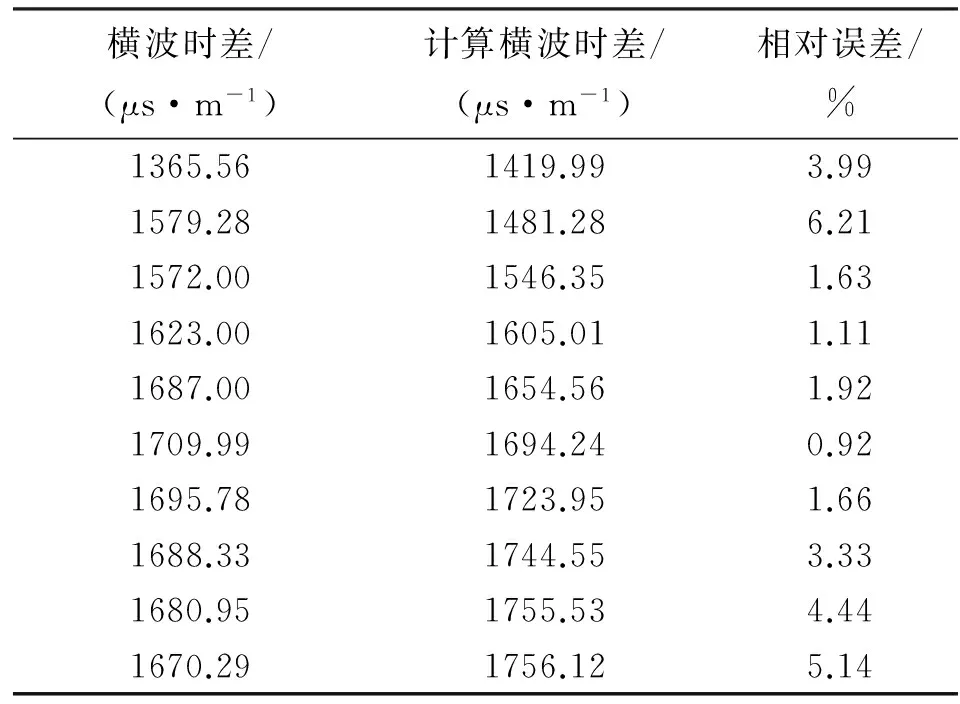
表3 煤层横波时差拟合模型误差分析数据表

续表3

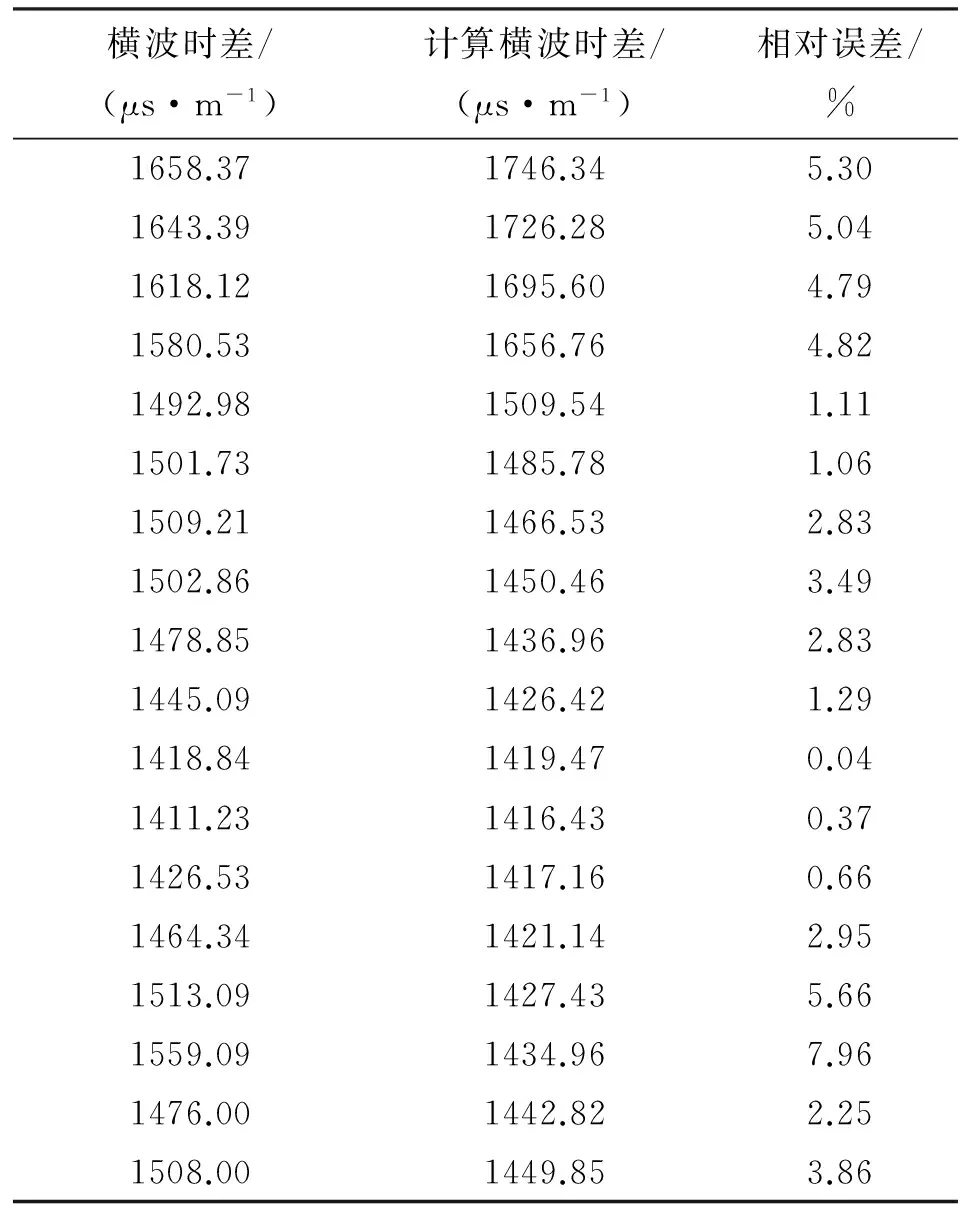
横波时差/(μs·m-1)计算横波时差/(μs·m-1)相对误差/%1658.371746.345.301643.391726.285.041618.121695.604.791580.531656.764.821492.981509.541.111501.731485.781.061509.211466.532.831502.861450.463.491478.851436.962.831445.091426.421.291418.841419.470.041411.231416.430.371426.531417.160.661464.341421.142.951513.091427.435.661559.091434.967.961476.001442.822.251508.001449.853.86

3 基于煤岩多矿物岩石体积物理反演横波时差

3.1 煤岩地层的多矿物组分体积物理模型

煤层组成成分复杂,如果忽略相对体积小于1%的成分(如二氧化硅、硝酸盐、菱铁矿、硫以及一些稀散元素等),那么可以把煤层粗略地看成是由固定碳、灰分、挥发分和水分4部分所组成。灰分包括泥质和矿物杂质,水分包括内在水分和外在水分。

多矿物组分地层体积模型的实际地层是由多种矿物和流体组成的混合物,利用常规测井资料采用复杂岩性分析程序,除挥发分外,还可求解2种主要矿物组分(固定碳和灰分)。

将煤层视为由固定碳(带有吸附的气体)、灰分、挥发分组成的饱含流体的介质模型,且固体骨架为弹性固体、流体可压缩且没有黏性,则地层模型如表4所示。其中固体包括固定碳、灰分和挥发分,流体为孔隙和割理中的水分,于是煤层的体积模型为

Vc+Va+Vv+Vw=1

(9)

式中,Va、Vc、Vw、Vv分别是灰分、固定碳、水分、挥发分的体积百分数。

3.2 横波速度反演算法步骤

第1步:首先根据表4中煤岩的多矿物地层组分体积模型,利用测井资料计算煤岩的组分。

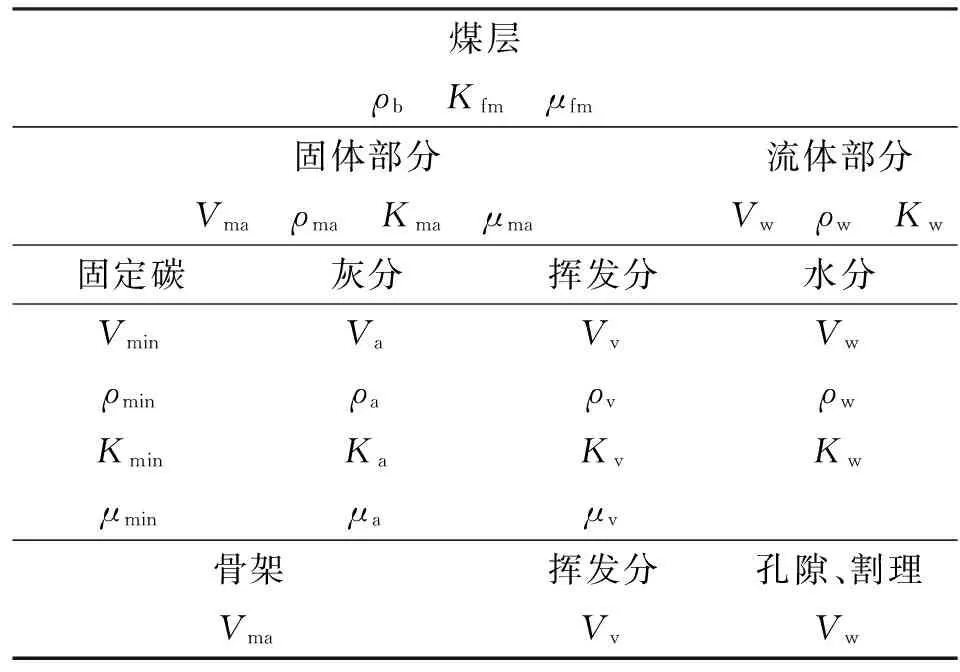
表4 煤岩多矿物地层组分体积模型

注:Kfm、μfm分别为煤层的体积模量、剪切模量。

(1) 输入中子、密度及纵波时差测井资料。通过交会图分析,确定煤层的固定碳、灰分参数及用于矿物交会分析的测井曲线校正量。

(2) 根据表4输入固定碳、灰分、挥发分和水分的体积模量、剪切模量、密度参数。

(3) 采用复杂岩性地层组分计算方法,计算固定碳、水分、灰分和挥发分等参数。

根据测井体积模型的基本思想,可得到煤层测井响应方程。

时差 Δt=VaΔta+VcΔtc+VwΔtw+VvΔtv

(10)

密度ρ=Vaρa+Vcρc+Vwρw+Vvρv

(11)

中子φN=Vaφa+Vcφc+Vwφw+Vvφv

(12)

式中,ρa、ρc、ρw、ρv分别是灰分、固定碳、水分、挥发分的密度值;Δta、Δtc、Δtw、Δtv分别是灰分、固定碳、水分、挥发分的声波时差值;φa、φc、φw、φv分别是灰分、固定碳、水分、挥发分的补偿中子值。

根据式(9),结合密度、声波及中子测井资料即可求取煤层中各组分的含量。

第2步:根据煤岩地层组分,利用Voight-Ruess-Hill模型[15]计算灰分、固定碳和挥发分的等效弹性模量Kma、μma。

(13)

(14)

式(13)、式(14)中,体积模量KV和剪切模量μV可由Voight等应变模型[15]求取;岩石体积模量KR和剪切模量μR可由Ruess等应力模型[16]计算。

第3步:以纵波为约束条件估算横波速度。

利用纵波速度Vp作为约束估算β系数。依据Biot-Gassmann理论[17]可以推导出

(15)

将式(15)化成一元二次方程或略去二次项即可算出β。

利用β、μma、ρb根据式(16)计算横波速度Vs,其中ρb可根据Vma和Vw的密度进行加权得出或直接采用密度测井值。

(16)

3.3 横波时差反演实例分析

利用上述方法对研究区煤层进行了横波时差反演处理。图4是研究区内×1井煤岩段横波时差反演实例。由图4可见,700～702 m煤层段反演的横波时差基本与测量横波时差一致,说明该方法在煤岩地层中的适用性和有效性;而704～707 m煤层段误差较大,分析其原因是由于该井段扩径较为严重,密度和纵波时差尽管作了扩径影响校正,但未必能还原真实的密度和纵波时差特性,致使利用密度和纵波时差反演的横波时差有一定的误差。

4 结论与建议

(1) 给出了3种构建煤岩横波时差测井曲线的方法,纵波和密度测井构建法较为简单、直观,但误差偏大;岩性指示曲线法和多矿物组分体积模型法均能较好地对煤层横波时差曲线进行估算,但多矿物组分体积模型中的参数求取相对较难。

(2) 针对煤储层测井曲线易受扩径等诸多环境因素的影响,建议在构建煤层横波时差预测模型前作好测井环境影响校正的同时,对其建模数据进行筛选,以提高横波时差的估算精度。

参考文献:

[1] Franklyn K Levin. 由纵波和转换波资料估计横波速度 [J]. 张仪宁译. 石油物探译丛, 1999, 5: 47-49.

[2] 赵靖舟, 刘之的, 时保宏, 等. 鄂东气田煤层气储层综合评价报告 [R]. 西安: 西安石油大学, 2012.

[3] 徐佳, 庞巨丰, 张茜. 从声波全波列测井曲线提取横波时差的计算方法分析 [J]. 计量与测试技术, 2010, 37(9): 47-51.

[4] 王玉梅, 苗永康, 孟宪军, 等. 岩石物理横波速度曲线计算技术 [J]. 油气地质与采收率, 2006, 13(4): 94-96.

[5] 李敬功. 利用常规测井资料计算气藏横波速度 [J]. 岩性油气藏, 2007, 19(2): 67-70.

[6] 郭栋, 印兴耀, 吴国忱. 横波速度计算方法与应用 [J]. 石油地球物理勘探, 2007, 42(5): 535-538.

[7] 云美厚, 管志宁. 储层条件下砂岩纵波和横波速度的理论计算 [J]. 石油物探, 2002, 41(3): 289-292.

[8] 张小庆, 桂志先. 岩石中纵横波速度关系研究 [J]. 石油天然气学报: 江汉石油学院学报, 2006, 28(4): 255-257.

[9] 马中高, 解吉高. 岩石的纵、横波速度与密度的规律研究 [J]. 地球物理学进展, 2005, 20(4): 905-910.

[10] 杨青山, 卢艳, 梁兵. 横波速度测井曲线重构方法 [J]. 大庆石油地质与开发, 2011, 30(5): 163-166.

[11] 姜传金, 马学辉, 周恩红. 拟合声波曲线构建的意义及应用 [J]. 大庆石油地质与开发, 2004, 23(1): 12-14.

[12] Biot M A. Theory of Propagation of Elastic Waves in a Fluid Saturated Porous Solid Frequency Range [J]. The Journal of the Acoustical Society of America, 1956, 28: 168-178.

[13] 郑雷清. 横波参数构建技术在岩性油气藏勘探中的应用 [J]. 新疆石油天然气, 2011, 7(4): 7-10.

[14] 孙玉凯, 郑雷清. 基于常规测井资料的横波时差估算方法及应用 [J]. 新疆石油地质, 2009, 30(4): 521-522.

[15] Voigt W. Lehrbuch der Kristallphysik [Z]. Teunber Verlag, Leipzig, 1990.

[16] Reuss A. Berechnung der Fliegrenze Von Misch Kristallen [J]. Angew Mathem U Mech, 1929, 9(1): 49-58.

[17] Gassmann F. Elastic Waves Through a Packing of Spheres [J]. Geophysics, 1951, 6: 673-682.