铸体薄片孔隙参数提取及其对饱和度指数的影响

范宜仁, 徐拥军, 范卓颖, 葛新民

(1.中国石油大学地球科学与技术学院, 山东 青岛 266555; 2.中国石油大学CNPC测井重点实验室, 山东 青岛 266555)

0 引 言

铸体薄片是将染色树脂或液态胶在真空状态下灌注到岩石的孔隙空间,在一定的温度和压力下使树脂或液态胶固结,然后磨制成岩石薄片,再在显微镜下观察孔隙、喉道及其相互连通、配合的二维空间结构的一种孔隙结构评价方法。铸体薄片对样品形状、尺寸要求低,且处理简单[1-5]。本文介绍了阈值分割、数学形态学滤波等算法在铸体薄片孔隙信息提取、图像增强等方面的应用,引入两点相关函数法对骨架-孔隙两相介质进行分析,得到了面孔隙度、比表面、平均孔隙半径、平均颗粒半径等孔隙参数,并将计算结果与其他方法进行比较。在此基础上,重点研究了面孔隙度、比表面、平均颗粒-孔隙半径比对饱和度指数的影响,得到与微观孔隙结构有关的饱和度指数模型。

1 铸体薄片处理及图像增强方法

根据铸体与矿物、黏土的颜色差异及其对光的吸收和敏感性,选择合适的放大倍数对铸体薄片进行成像分析即可得到样品的形貌照片。铸体薄片通常以RGB的格式保存,由红、绿、蓝三基色构成。由图像学的理论可知,对一副RGB格式的铸体薄片其灰度值可以表示为[6]

Ic=fc(x,y) 0≤fc(x,y)≤255

(1)

式中,c表示为R、G、B。

孔隙、骨架和黏土在铸体薄片中具有不同的灰度特征。国际上通用蓝色液态胶进行薄片的灌注和压制。如图1所示,孔隙部分被注入蓝色胶体后呈蓝色特征。采用阈值分割算法,可将特征明显的岩石组分从二维图像中提取出来,阈值分割的操作算子T可表示[6]为

T(tlow,thigh)fc(x,y)=

(2)

式中,tlow、thigh分别表示某岩石组分灰度下、上限值。

图1 孔隙、骨架及黏土在铸体薄片中的像素特征

对于孔隙参数的定量计算,只需将孔隙信息从铸体薄片中提取出来即可。通过阈值分割后,铸体薄片变成0或1的像素矩阵,其中0代表骨架,1代表孔隙。

阈值分割算法的缺陷在于,当目标被分割在不同的子块时会存在明显的块状效应,将孔隙与骨架信息模糊化。数字形态学滤波是一种很好的去除块效应的方法,其基本思想是将图像看成是点的集合,用结构元素对其进行移位、交、并等集合运算。它具有膨胀、腐蚀、开启和闭合等4种最基本的运算[7-8]。

设A为图像集合,B为结构元素,则结构元素B对图像集合A的膨胀算法为

A⊕B{B+x∶⊂A}

(3)

式(3)是将结构元素B对图像集合A的所有像素作平移,然后对平移得到的结果作并运算。膨胀运算保留了原图的基本形状,但填平了原图边界上不平滑的凹陷部分。当结构元素和像素值为1时,即结构元素击中图像,输出1,否则输出0。

腐蚀算法为

AΘB{x∶B+x⊂A}

(4)

腐蚀运算将结构元素B平移x,但仍然包含在图像集合A内的所有点x组成。结构元素在整个图像区域平移的过程中,结构元素的原点到所有可能的图像像素点检查图像,当结构元素与图像的前景部分完全匹配时,即结构元素适合图像,输出1,否则输出0。

开启算法可以表示为

AoB=(AΘB)A⊕B

(5)

A被B开启运算就是图像集合A被结构元素B腐蚀后的结果再被B膨胀。开启运算可去掉图像中的一些孤立子域、毛刺和凸出部分,使图像更加平滑。

闭合运算可以表示为

A.B=A⊕BΘB

(6)

A被B闭合运算就是图像集合A被结构元素B膨胀后的结果再被B腐蚀。闭合运算沿着图像的外边缘填充,去除了凸向图像内部的尖角,填平缝隙,弥合孔洞和裂缝,能去除图像上的小孔和凸部,使断线连接,而总的位置和形态不变。

一个完整的形态学滤波过程包括开启运算和闭合运算,铸体薄片从孔隙信息提取到形态学滤波的过程见图2。

图2 铸体薄片数字图像处理及形态学滤波流程

2 相关函数理论及孔隙参数提取

岩石可近似成由骨架和孔隙组成的两相介质,可以采用指示函数法进行骨架和孔隙表征。d维欧氏空间(d)的孔隙-骨架两相介质的指示函数可定义为[9-14]

(7)

式中,Vi∈d表示欧氏空间内介质为孔隙;Vi∉d表示欧氏空间内介质为骨架;x为d空间的坐标。

对于用指示函数表示的骨架-孔隙两相系统,采用相关函数表示某相同时存在于空间内不同点的概率,对于孔隙,其n点相关函数表达式为

Sn(x1,x2,…,xn)=

(8)

式中,< >表示为总体平均。

对于各向同性介质,n点相关函数与各点的绝对坐标无关,仅与各点之间的相对位移有关,则式(8)可转换为[9]

Sn(x1,x2,…,xn)=Sn(x12,…,x1n)

(9)

式中,xij=xj-xi。根据多点相关函数的定义可知,对于孔隙,若n=1,则有

S1==φ

(10)

式中,φ为孔隙度。若n=2,则有

S2(x1,x2)=S2(r)==

(11)

式中,r=x2-x1。

Berryman等[9,11]研究表明,当r=0时,有

S2(0)=S1=φ

(12)

当r→∞时,有

φ2

(13)

从两点相关函数中还可得到比表面积s、平均孔隙半径rc、平均颗粒半径rg等。其计算公式分别为

(14)

(15)

Stephen C Blair等[12]认为,相关函数值最小时所对应的相关长度为1.3rg。研究采用该方法确定平均颗粒半径。

3 实验分析

经阈值分割及数字形态学滤波后,铸体薄片的灰度值为0或1。两点相关函数的离散形式可写成

(16)

式中,M、N为灰度图像在x和y方向的点数。结合式(12)至式(15)即可得到样品的相关函数图及面孔隙度、比表面s、平均孔隙半径rc、平均颗粒半径rg等。

选取10块样品开展了孔隙度、岩电、铸体薄片及压汞实验。实验环境为常温常压(25 ℃,1 MPa),饱和溶液为NaCl,为降低附加导电对岩电参数的影响,其浓度配置为50 000 mg/L,孔隙度的测量采用氦气法,电阻率的测量采用二极法,采用高速冷冻离心机进行岩石失水。图3为1号样品的阈值分割、形态学滤波、两点相关函数计算的全过程。应用同样的流程对其他样品进行处理并进行孔隙参数提取。表1为实验样品的常规物性、岩电及孔隙参数处理结果。

图3 1号样品铸体薄片处理及两点相关函数计算结果

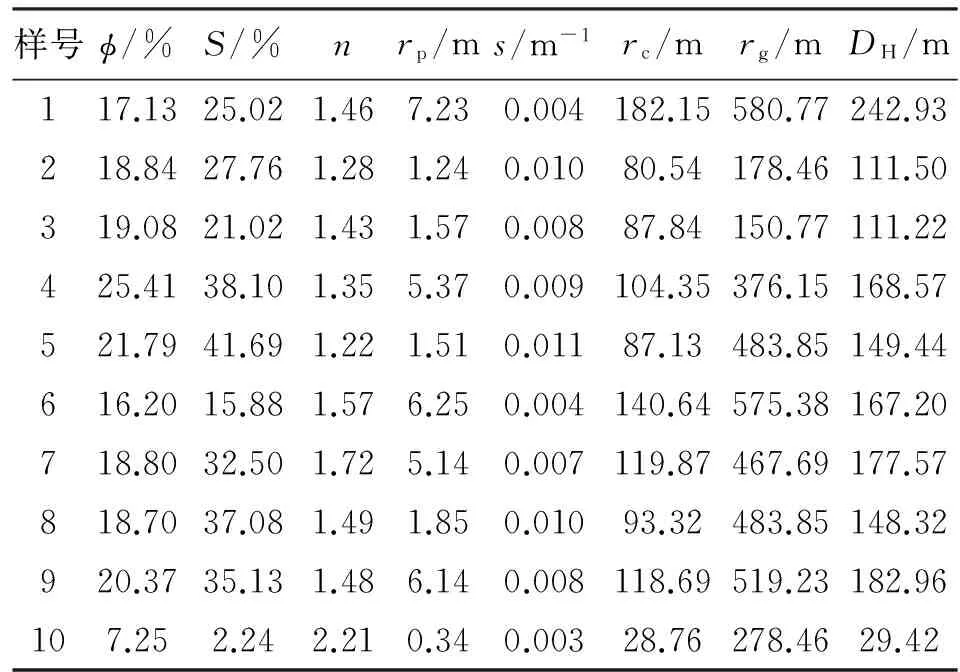
样号ϕ/%S/%nrp/ms/m-1rc/mrg/mDH/m117.1325.021.467.230.004182.15580.77242.93218.8427.761.281.240.01080.54178.46111.50319.0821.021.431.570.00887.84150.77111.22425.4138.101.355.370.009104.35376.15168.57521.7941.691.221.510.01187.13483.85149.44616.2015.881.576.250.004140.64575.38167.20718.8032.501.725.140.007119.87467.69177.57818.7037.081.491.850.01093.32483.85148.32920.3735.131.486.140.008118.69519.23182.96107.252.242.210.340.00328.76278.4629.42

图4为10块样品的铸体薄片处理孔隙度与气测孔隙度的对比。从图4可知,两者呈良好的线性关系,复相关系数为0.756,拟合公式为

φs=2.286φ-14.326

(17)

式中,φ为气测孔隙度,%;φs为薄片处理面孔率,%。

图4 铸体薄片处理孔隙度与气测孔隙度对比

图5 铸体薄片处理平均孔隙半径与压汞平均孔喉半径对比

图5是10块样品的铸体薄片处理的平均孔隙半径与压汞法得到的平均孔喉半径对比。从图5可知,两者的线性关系较好,其复相关系数为0.75。由于研究尺度的差别,铸体薄片处理的平均孔隙半径要远远大于压汞法平均孔喉半径。

rc=13.865×rmp+53.529

(18)

式中,rc为铸体薄片处理平均孔隙半径,μm;rmp为压汞法平均孔喉半径,μm。

以上分析表明,通过数字图像处理和两点相关函数法得到的孔隙参数与其他方法得到的孔隙参数具有一致性,可用表1的处理结果进行岩石的电学性质分析。图6是饱和度指数与比表面的相关关系图。从图6可知,饱和度指数随着比表面的增大而减小,两者呈良好的幂函数关系,其复相关系数为0.56,拟合公式为

n=0.38/s0.275

(19)

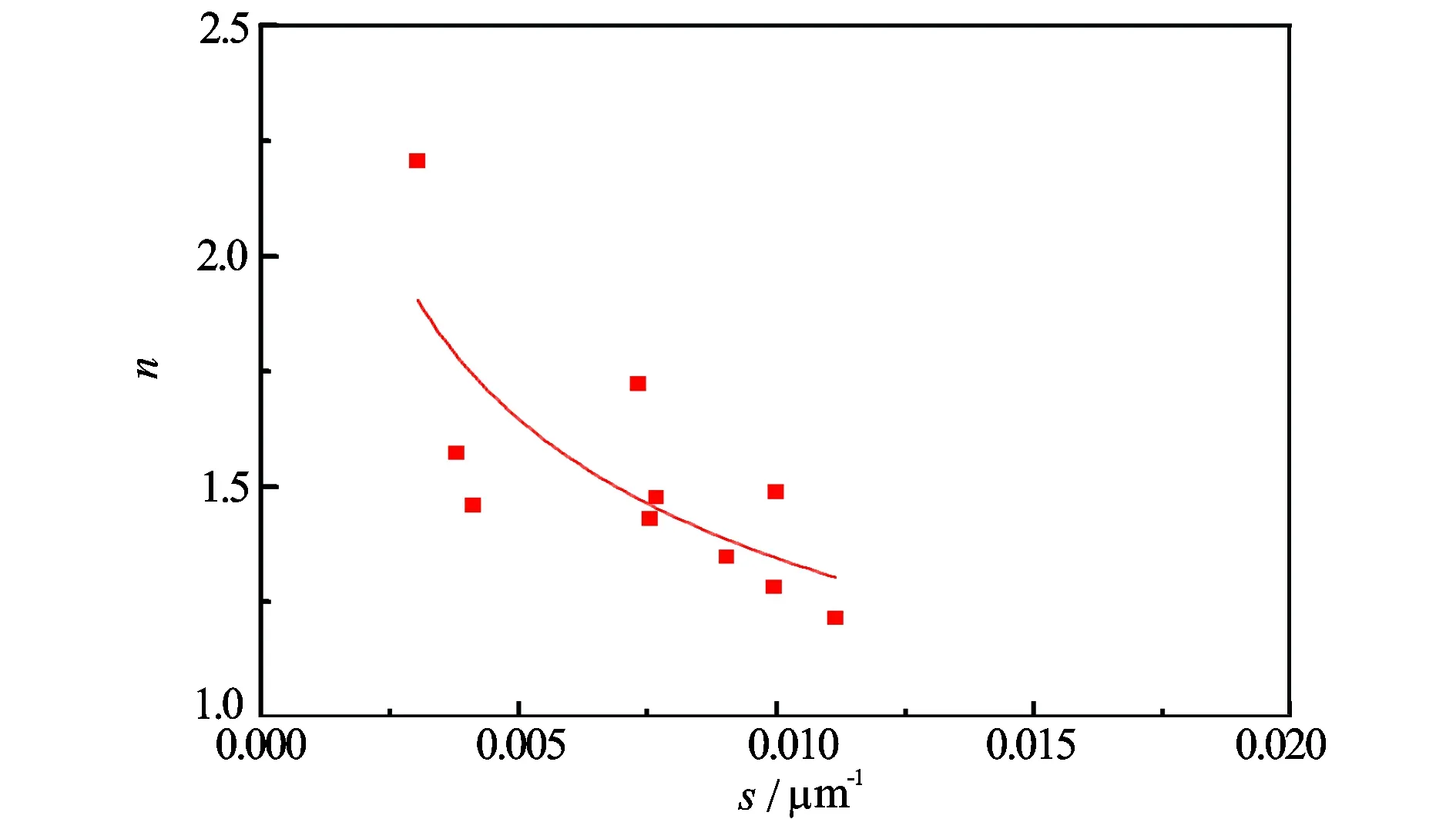
图6 饱和度指数与比表面相关关系

岩石的导电及渗流性质还受到孔隙半径、颗粒半径等因素的共同影响。为了综合考虑这些参数对饱和度指数的贡献,构造平均颗粒-孔隙半径比表征孔喉的连通程度。图7是饱和度指数与平均颗粒-孔隙半径比的关系图。从图7可知,饱和度指数随着平均颗粒-孔隙半径比的增大而减小,两者呈良好的线性关系,复相关系数为0.53。经拟合,饱和度指数与平均颗粒-孔隙半径比的关系为

(20)

图7 饱和度指数与平均颗粒-孔隙半径比关系

图8 饱和度指数与面孔隙度相关关系

图8是饱和度指数与面孔隙度的相关关系图。从图8可知,饱和度指数随着孔隙度的增大而减小。经拟合,得到饱和度指数与面孔隙度的关系为

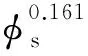
(21)

结合式(19)至式(21),将饱和度指数写为

(22)

式中,a、b、c、d均为拟合参数,无量纲,可用最小二乘拟合法得到。图9是根据式(22)拟合得到的饱和度指数与实验测量得到的饱和度指数对比图,两者分布在45 °线左右,经统计,其平均绝对误差为0.067,平均相对误差为4.7%,精度非常高。

图9 计算饱和度指数与实测饱和度指数对比

4 结 论

(1) 铸体薄片含有丰富的孔隙参数等信息,通过数字图像处理与两点相关函数理论得到的面孔隙度、平均孔隙半径等与其它方法所得的参数呈良好的线性正相关关系。

(2) 饱和度指数与面孔隙度、岩石比表面积、平均颗粒-孔隙半径比等密切相关,随着面孔隙度、岩石比表面积和平均颗粒-孔隙半径的增大而呈幂函数衰减。

(3) 通过引入面孔隙度、岩石比表面积及平均颗粒-孔隙半径比等微观参数建立的饱和度指数模型精度较高,计算的饱和度指数与实测饱和度指数基本相等。

参考文献:

[1] Shelley D. Optical Mineralogy [M]. 2nd ed. New Zealand: Elsevier Press, 1985.

[2] Barber D J. Demountable Polished Extra-thin Sections and Their Use in Transmission Electron Microscopy [J]. Mineralogical Magazine, 1981, 44: 357-359.

[3] Anderson A N, McBratney A B, FitzPatrick E A. Soil mass, Surface, and Spectral Fractal Dimensions Estimated from Thin Section Photographs [J]. Soil Sci Soc Am J, 1996, 60: 962-969.

[4] Grove C, Jerram D A. An ImageJ Macro to Quantify Total Optical Porosity from Blue-stained Thin Sections [J]. Journal of Computers and Geosciences, 2011, 37, jPOR: 1850-1859.

[5] 张丽霞. 高蒙皂石砂岩铸体薄片制片新方法 [J]. 新疆石油地质, 2009, 30(6): 709-780.

[6] 冈萨雷斯. 数字图像处理 [M]. 北京: 电子工业出版社, 2003.

[7] 崔屹. 图象处理与分析-数学形态学方法应用 [M]. 北京: 科学出版社, 2000.

[8] Serra J. Image Analysis and Mathematical Morphology [M]. London: Academic Press, 1982.

[9] Berryman J G. Measurement of Spatial Correlation Functions Using Image Processing Techniques [J]. J Appl Phys, 1985, 57: 2374-2384.

[10] Berryman J G, Blair S C. Use of Digital Image Analysis to Estimate Fluid Permeability of Porous Materials: Application of Two Point Correlation Functions [J]. J Appl Phys, 1986, 60: 1930-1938.

[11] Berryman J G. Relationship Between Specific Surface Area and Spatial Correlation Functions for Anisotropic Porous Media [J]. J Math Phys, 1987, 28: 244-245.

[12] Stephen C Blair, Patricia A Berge, James G Berryman. Using Two-point Correlation Functions to Characterize Microgeometry and Estimate Permeabilities of Sandstones and Porous Glass [J]. Journal of Geophysical Research, 1996, 101(B9): 20359-20375.

[13] Ridgway R, Irfanoglu O, Machiraju R, et al. Image Segmentation with Tensor-based Classification ofn-point Correlation Functions [C]∥ Proceedings of the Microscopic Image Analysis with Applications in Biology (MIAAB) Workshop in MICCAI, Dec 2006.

[14] Jiao Y, Stillinger F H, Torquato S. Modeling Heterogeneous Materials Via Two-point Correlation Functions: Basic Principles [J]. Physical Review E (Statistical, Nonlinear, and Soft Matter Physics), 2007, 76(3): 31110-31146.