高墩大跨连续刚构弯桥结构动力分析

肖勇刚，周泽箭

在众多桥型中，连续刚构桥以其跨径大、主墩与主梁固结、无支座及桥面连续且行车平顺等特点受到青睐［1］。到目前为止，尽管有很多学者针对高墩大跨桥梁做了大量的研究［2－6］，但绝大部分是针对直桥的静力特性进行分析的，对弯桥分析较少，且研究大多针对的是曲率半径的变化对弯扭耦合效应的影响［7－10］，对大曲率半径下桥梁结构的动力特性和稳定性分析得比较少。而在实际建设中，为了使弯扭耦合效应降低，所采用的曲率半径大多是较大的，且在实际施工中一些跨越地区为地形所限，往往采用高墩设计，有时墩高可达百米以上。因此，对大曲率半径大跨高墩连续刚构弯桥动力特性进行研究是十分有必要的，具有一定的现实意义。

西牛大桥桥长698.08m，桥墩最高74.029m。主桥采用70＋2×125＋70m预应力混凝土变截面连续刚构桥，主桥箱梁桥主墩和过渡墩为薄壁空心墩，桩基采用灌注桩基础，曲率半径为1 550m。主桥布置如图1所示。

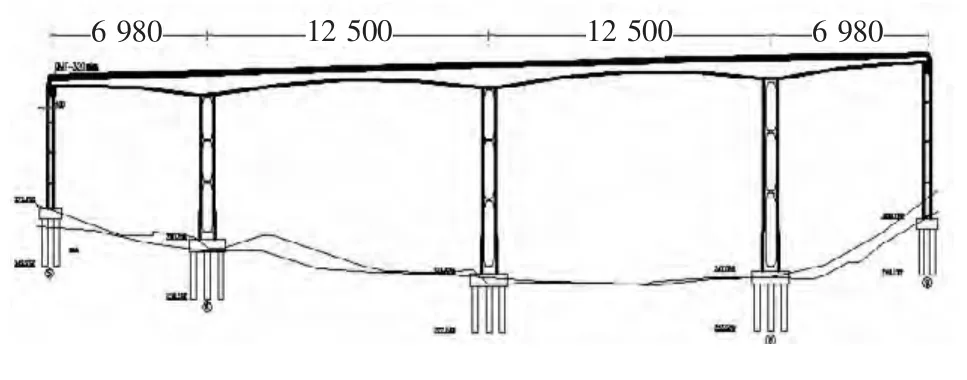
图1 大桥主跨布置（单位：cm）Fig.1 Main span of the bridge layout（unit：cm）

1 模型的建立

结构分析模型一定要能够反映实际结构的特点，能够正确反映各重要工况下结构的特性及荷载状况，因此，在建立全桥结构模型和最大悬臂状态模型时，其几何特性、边界条件及荷载状态必须与实际结构相对应。利用MIDAS Civil2010软件，建立全桥和最大悬臂状态有限元模型，曲率半径为1 550m。根据设计图纸，将西牛大桥划分为222个节点和212个单元，输入320束预应力刚束，定义自重、预应力、铺装、挂篮、湿重及时间函数6种静力荷载，2种车道移动荷载，21个施工阶段。西牛大桥的有限元模型如图2所示。

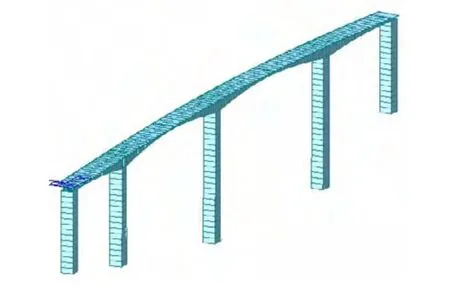
图2 西牛大桥计算模型Fig.2 The model of Xiniu Bridge

为了使研究有代表性，假想并增建了曲率半径为500，1 000和2 000m的弯梁桥，用4种不同曲率半径的桥梁进行结构动力分析。增建的弯梁桥除曲率半径与西牛大桥的不一样外，其余条件（如：跨径、材料及约束条件等）均与西牛大桥完全一致。运用有限元软件对不同曲率半径的弯梁桥进行动力分析，以期反映连续刚构桥在相同影响因素作用下曲率半径对其动力特性的影响。建立模型时，固定刚构桥的跨径不变，即跨径布置为75＋125＋125＋75m。通过建立4种不同曲率半径的有限元模型，来计算分析刚构弯桥结构的动力特性，它们的有限元模型如图3所示。

图3 不同曲率半径计算模型Fig.3 Different curvature radius calculation model

2 结构动力特性分析

由于曲率的存在，使得曲线梁桥产生一个主要受力特性：弯扭耦合（即在动力作用下，曲线梁桥中同时产生弯矩和扭矩，并且相互影响［3］）。与直线桥梁相比，曲线桥梁的动力特性有很大的不同。曲率半径是影响曲线桥梁动力特性的重要参数，因此，分析曲率半径的变化对曲线桥梁动力特性的影响是非常必要的。作者拟对结构的动力特性进行分析，得出不同曲率半径下结构最大悬臂状态和全桥状态的自振周期与振型，并采用反应谱分析方法，对不同曲率半径结构墩身关键点在顺桥向和横桥向地震作用下的变形进行分析。

2.1 全桥状态动力分析

全桥状态前5阶自振频率变化曲线如图4所示，第1阶振型如图5所示。

由全桥状态动力特性分析可知：

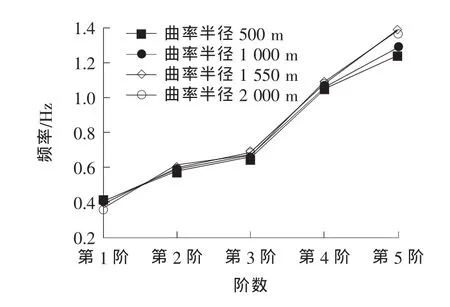
图4 全桥状态频率变化曲线Fig.4 Full bridge state frequency curve

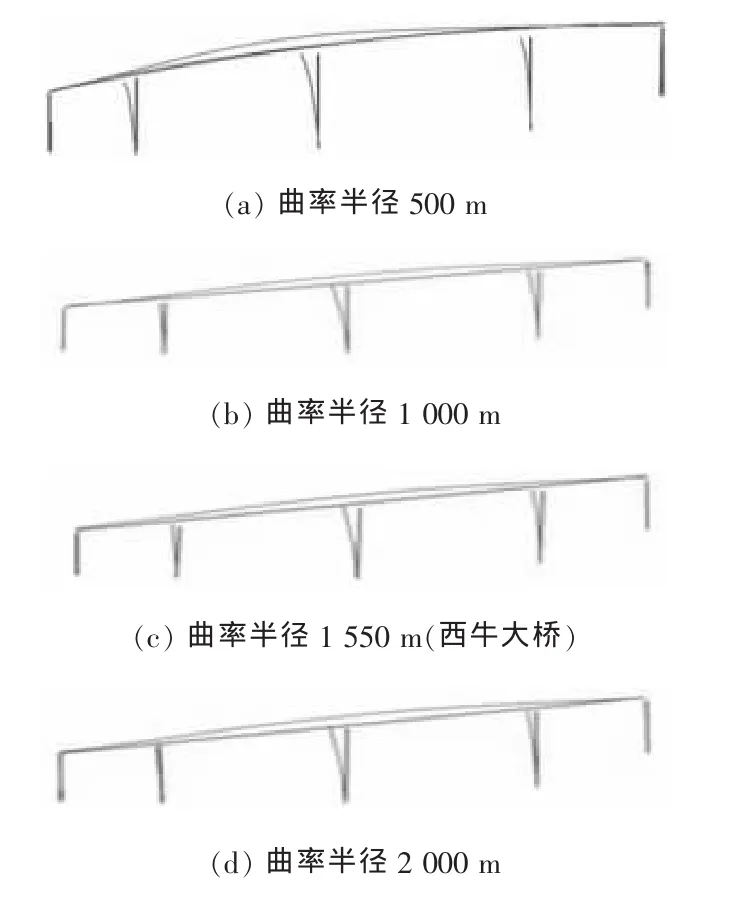
图5 全桥状态第1阶振型Fig.5 The first order vibration type with full bridge state

1）随着曲率半径的增大，结构的基频逐渐减小，从图4，5中可以看出，第1阶振型以横向振动为主，振型相差不大。随着曲率半径的增加，墩身横向弯曲的程度有所增加。基频减小的原因是：曲梁的横向振动类似于拱的面内弯曲振动，增大了梁的横向振动刚度，使结构变得更刚。随着曲率半径的增大，这种拱的作用逐渐减弱［5］。分析振型可以看出，第2，4和5阶振型均以纵向振动为主。随着曲率半径的增加，墩身纵向弯曲的程度略有所减小。这两种情况说明，随着曲率半径的增大，桥梁横向刚度减少，但纵向刚度增大。随着曲率半径的增大，结构的频率呈现增大的趋势。这说明随着曲率半径的增大，结构的稳定性有所增强。

2）对曲线连续刚构桥而言，纯粹某一方向的振型是不存在的，只是某一方向的分量所占比重相对大而已［4］。查看结构的振型参与质量可知，随着曲率半径的增大，结构第1阶振型对X方向的振型贡献率增大，对Y方向的振型贡献率随之减小。当第40阶时，X方向上振型参与质量与Y方向上振型参与质量均超过90%，满足规范要求。这种变化趋势说明，当曲率半径变小时，振型耦合影响越来越大，故对曲线梁桥的地震响应考虑水平双向地震动的耦合是必要的［4］。

2.2 最大悬臂状态动力分析

在刚构桥的施工阶段，由于存在结构的刚度较小、动力响应大及稳定性差等不利因素的影响，会使施工状态出现比成桥状态更为不利的状况，因此，对刚构桥的施工过程尤其是对最大悬臂施工状态进行动力分析，在安全施工和安全运营方面有着重要的意义。为使研究有代表性，选取最高墩7号墩最大悬臂状态进行动力分析，观察在高墩影响下，不同曲率半径结构的动力特性。前5阶自振频率变化曲线和第1阶振型分别如图6，7所示。

图6 最大悬臂状态频率变化曲线Fig.6 The maximum cantilever state frequency curve

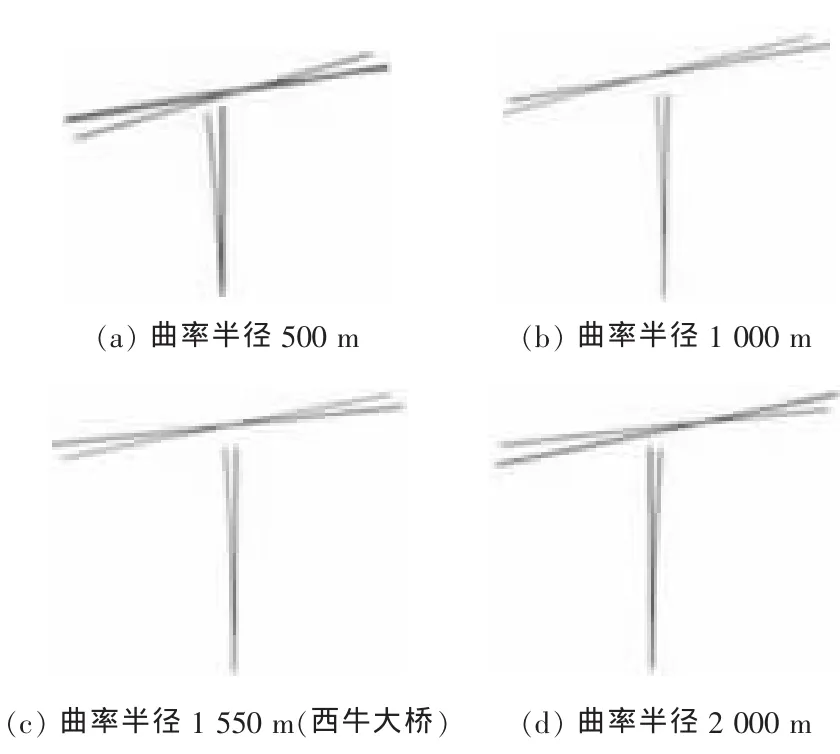
图7 最大悬臂状态第1阶振型Fig.7 The first order vibration type with the maximum cantilever state

由最大悬臂状态动力特性分析可知：

1）在最大悬臂工况时，不同曲率半径的第1阶振型都是墩身沿着桥纵向的弯曲且有主梁绕桥横轴旋转摆动。分析前几个工况可以看出，从主梁施工开始到最大悬臂状态为止，此模态一直保持这种变化规律，4种曲率半径下结构基本模态相差不大。随着曲率半径的增加，主梁的横向摆动也变得更加明显。但是，墩身纵向弯曲的程度有所减小。这说明随着曲率半径的增加，横向振动刚度逐渐减少，纵向刚度逐渐增大。

2）随着曲率半径的增大，结构基频频率逐渐增大，与全桥状态结果相反。这是因为最大悬臂状态结构悬臂端没有受到约束，基频的振动形态为纵向振动，这样曲率半径形成的类似拱的作用就不明显。而随着曲率半径的增加，最大悬臂结构的稳定性得到加强，使得基频逐渐增大。与全桥状态结构基频相比，最大悬臂状态下结构自振频率较低（基频分别为0.229，0.237，0.255和0.288Hz）。这说明最大悬臂状态结构体系较柔。这样，当在风荷载或地震荷载作用下，易引起较大的变形，也易引起结构的共振。因此，在最大悬臂状态下施工时，应该采取一定的措施，对结构做好防风、抗震工作。

2.3 反应谱分析

采用CQC法，叠加各振型结构的地震响应［7］。根据西牛大桥设计图纸，按地震动峰值加速度0.05g，地震基本烈度Ⅵ度，抗震设防按Ⅶ度设防，环境类别二类场地，建立反应谱函数。考虑弹性状态，则4种曲率半径桥梁结构的水平地震加速度曲线如图8所示。按《公路桥梁抗震设计细则》（JTGT B02－01－2008），广西桂林荔浦县所属设计地震分组为第一组，特征周期为0.35s。

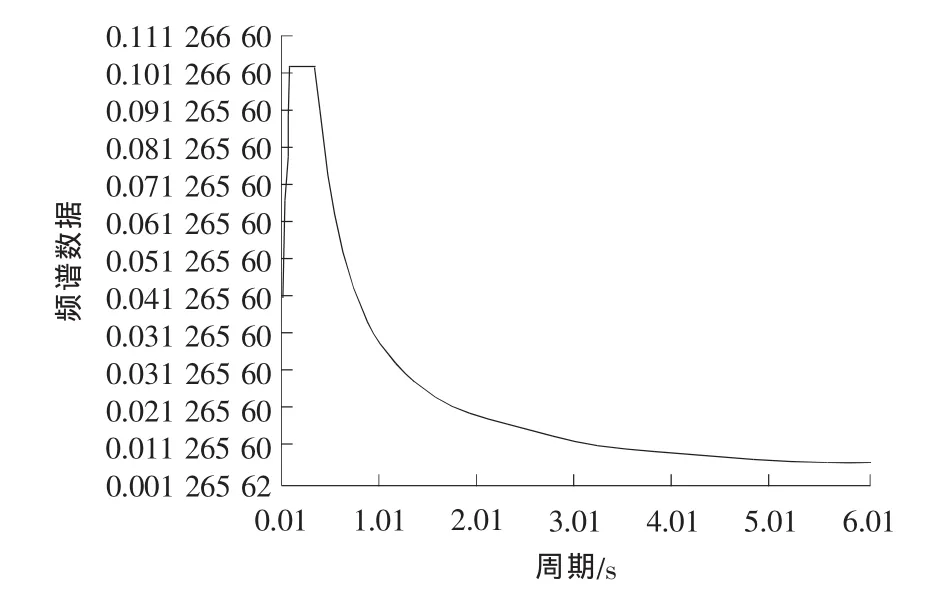
图8 水平地震加速度曲线Fig.8 Horizontal earthquake acceleration curve

在抗震分析中，不采用子空间迭代法，而用多重Ritz向量法。其原因是多重Ritz向量法认可结构动态响应是空间荷载分布的函数，考虑动力荷载的空间分布，能避免漏掉可能激起的振型和引入不可能激起的振型，能够显著提高计算效率。故采用多重Ritz向量法进行分析，分别考虑X，Y方向上20阶模态，定义顺桥向和横桥向两个反应谱工况进行求解。4种曲率半径的基本模态相似，选取西牛大桥（R＝1 550m）变形作为示例，其变形如图9所示。考虑到高墩对动力特性具有扩大作用，选取最高墩7号墩进行分析，使得分析具有代表意义。纵、横向墩身变形曲线分别如图10，11所示。

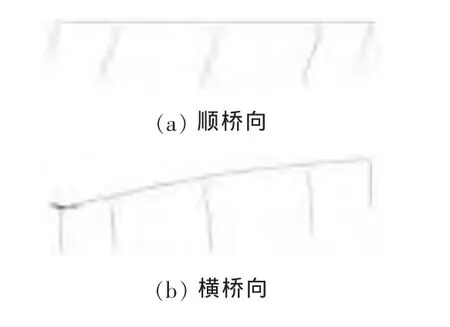
图9 纵、横向地震单向激励下桥梁变形Fig.9 Vertical and horizontal seismic excitation deformation bridge

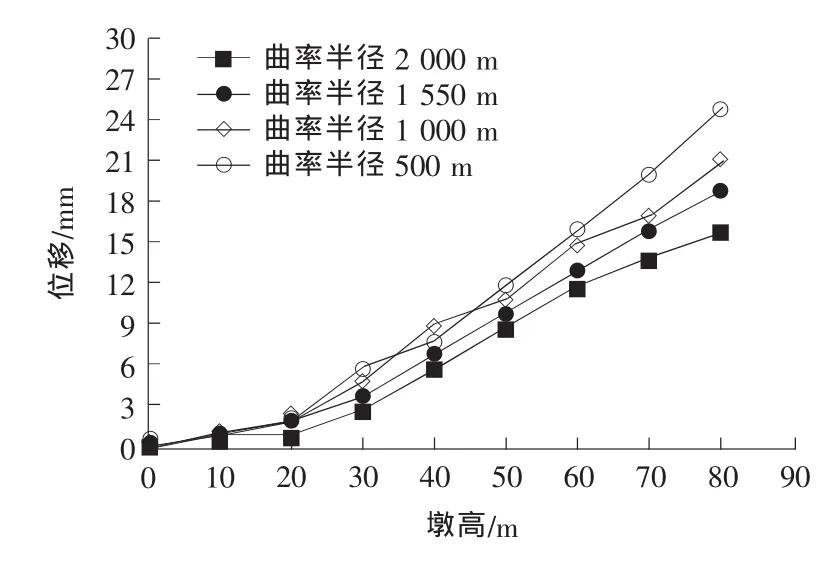
图10 顺桥向地震激励下7号墩墩身变形Fig.10 The longitudinal deformation under earthquake excitation of pier No.7

由墩身变形图可知：在纵向单向激励下，随着曲率半径的增大，墩身位移均不同程度的减小。在横向单向激励下，随着曲率半径的增大，墩身位移均不同程度的增大。分析数值可知，横向激励下墩身位移大于纵向激励下墩身位移，说明横向刚度较纵向刚度小。在不考虑弯矩扭转的前提下，曲线桥的曲率半径越小，抗震性能越强。

图11 横桥向地震激励下7号墩墩身变形Fig.11 Transverse seismic excitation deformation of pier No.7

3 结论

通过对不同曲率半径下全桥动力特性和最大悬臂状态动力特性进行分析发现：在全桥状态下，随着曲率半径的增大，桥梁横向刚度减少，但纵向刚度增大，第1阶频率逐渐减小，但频率随着曲率半径的增大而增大。最大悬臂状态下，随着曲率半径的增大，基频也随之增大，频率也是呈现增大的趋势。由反应谱分析可知，随着曲率半径的减小，在不考虑弯扭耦合效应的前提下，即桥梁越弯曲，抗震性能越强。但是，在设计中需要考虑桥梁曲率半径。曲率半径越小，会引起弯扭耦合效应越大。同时，高墩对弯扭耦合还有一定的放大作用。因此，对由曲率半径引起的耦合效应也应该予以考虑，综合各因素比较，西牛大桥采用曲率半径1 550m是一个合理的选择。

（

）：

［1］ 王钧利，贺栓海.大跨径连续刚构桥高墩设计与稳定性［J］.长安大学学报：自然科学版，2006，26（5）：35－39.（WANG Jun－li，HE Shuan－hai.Design and stability of large span continuous rigid frame bridge with high piers［J］.Journal of Chang’an University：Natural Science Edition，2006，26（5）：35－39.（in Chinese））

［2］ 孟会英，陈秀云，雷世发.预应力混凝土连续弯箱梁桥动力特性分析与试验研究［J］.世界地震工程，2008，24（1）：128－131.（MENG Hui－ying，CHEN Xiu－yun，LEI Shi－fa.Dynamic analyses and experimental studies on the prestressed concrete continuous curved box－girders［J］.Word Earthquake Engineering，2008，24（1）：128－131.（in Chinese））

［3］ 魏利军.基于梁格法的曲线箱梁桥弯扭耦合效应研究［D］.长安：长安大学，2011.（WEI Li－jun.Study on lateral torsional coupling effect of curved box girder bridges based on the grillage method［D］.Chang’an：Chang’an University，2011.（in Chinese））

［4］ 代攀，杨涛，胡大琳.高墩大跨曲线连续刚构地震响应分析［J］.世界地震工程，2009，25（4）：181－187.（DAI Pan，YANG Tao，HU Da－lin.The seismic response analysis of curved continuous rigid frame bridges with high piers and long span［J］.World Earthquake Engineering，2009，25（4）：181－187.（in Chinese））

［5］ 彭大文，罗朝专，林志平.整体式桥台曲线箱梁桥的动力特性研究［J］.公路交通科技，2010.27（2）：54－59.（PENG Da－wen，LUO Chao－zhuan，LIN Zhi－ping.Research on dynamic characteristics of integral abutment curved box girder bridge［J］.Journal of Highway and Transportation Research and Development，2010，27（2）：54－59.（in Chinese））

［6］ 牛俊武，郭楠楠，马文涛.不同曲率半径对高墩大跨径连续刚构桥抗震性能影响分析［J］.公路，2011（9）：137－141.（NIU Jun－wu，GUO Nan－nan，MA Wentao.Analysis of different curvature radius on the high pier and long－span continuous rigid frame bridge seismic performance［J］.Highway，2011（9）：137－141.（in Chinese））

［7］ 余报楚，谢斌.广东金马大桥多点非平稳随机激励下地震响应研究［J］.土木工程，2013（2）：89－95.（YU Bao－chu，XIE Bing.Non－stationary random excitation seismic response of Jinma Bridge in Guangdong［J］.Journal of Civil Engineering，2013（2）：89－95.（in Chinese））

［8］ 邓鲲.高墩大跨连续刚构桥的动力特性分析［J］.交通科技，2008（6）：10－12.（DENG Kun.Analysis of dynamic characteristics for high pier－long span continual rigid frame bridge［J］.Transportation Science ＆Technology，2008（6）：10－12.（in Chinese））

［9］ Abdel－salam M N，Heins C P.Seismic response of curved steel box girder bridges［J］.Journal of Structural Engineering，1988，114（12）：2790－2800.

［10］ Samaan M，Kennedy J B，Sennah K.Dynamic analysis of curved continuous multiple－box girder bridges［J］.Journal of Bridge Engineering，2007，12（2）：184－193.