基于网络最短路径的铁路购票智能推荐算法研究
2014-05-08刘胜来李瑞敏
刘胜来,李瑞敏
(清华大学 土木工程系,北京 100084)
2013年春运期间,全国铁路部门共发送2.4亿人次[1],如此庞大的出行量也让买票成了一个难题。自网上售票以来,车站买票排队问题已经大为缓解,但是无票可买的问题仍然大量存在。而另一方面,部分铁路路段却出现了大量空座现象。由此,可以考虑通过换乘的方式,变直达为换乘,实现相应的出行。
事实上,目前已有个别出行者针对春运期间一票难求的问题,通过换乘来解决长途出行,而最终可能在多支付一定费用的情况下,不仅解决了出行的问题,而且还可能缩短行程时间[2]。在当前我国高速铁路网基本覆盖主要干线的情况下,部分二、三线城市之间的出行通过普速铁路与高速铁路的结合,可能实现更短的出行时间。
通过换乘实现出行并可能减少出行时间的实施需要有合理计算方法的支持。本文基于铁路网络的路径优化问题,根据已有铁路列车时刻表,给出了一种行之有效的最优路径求解的解决方案。
本方案基于现行铁道部门实际拥有的线路信息,通过计算优化,提供给用户智能化的线路推荐服务。可以自动生成两地间到达速度最快和花费费用最少的两种方案,帮助用户达到省钱和省时的目的。
1 研究现状
为用户提供换乘策略并给出旅行路线指导方案,这个功能已经有不少网站正在尝试,但却能发现不少可改进的地方。
1.1 12306网站
铁道部门购票唯一官方网站12306提供了一项铁路旅程规划功能,如图1所示,但却没有达到相应的旅程规划的实用性。

图1 12306网站铁路旅程规划功能界面截图(2013.7.10)
从输入界面中可以看到,它需要用户手动输入换乘城市,甚至需要换乘日期,而且只能换乘一次。其实质仅相当于在余票查询窗口的两次搜索功能放在一个窗口显示,并没有实现真正的旅途规划,更不可能设计出多次换乘的乘车路线。除了它能及时根据网站数据查出现在是否有票外,没有太多实际参考价值。
1.2 火车网(www.huoche.com.cn)
火车网的车次查询功能通过输入起始与终止站点即可查询到需要的车次,对没有直达车次的则提供一系列中转方案。
在提供的多种方案中,给出了一个总用时的指标,但根据12306网站提供的列车信息核查,这个总时间实际指的是两列列车运行时间的和,换乘中间的时间差并没有考虑。因此该网站给出的推荐出行方案参考价值不大。另外,该网站与12306网站还存在数据误差,其实用性有限。
针对上述不足,本文结合网络最短路径算法,研究开发了一种更为合理、实用并且准确的路线规划方法,并通过计算机程序予以实现。
2 核心算法
2.1 站点与列车线路网络化
以城市站点为网络中的节点,列车为两站间的线段,每条线属性包含车次名称、出发及到达时间、运行时间和票价,这样便形成了基本的网络。
2.2 不同座位等级区分
硬座票、硬卧票分别对应动车的二等座和一等座,在选择票价最优时需先选择座位等级,即硬座(二等座)级或硬卧(一等座)级,其他如软卧等座位级别本文暂不考虑。根据每条线路的票价属性,座位等级用于票价最低的线路优化。
2.3 得到票价最低线路或票价最低排名前N的路线
根据每条线路赋给的票价属性,根据选择的座位等级,直接使用网络最短路径算法(Dijkstra算法[3])可立即得到票价最低的路线图。另外,考虑到实际要求,通过对Dijkstra算法改进,用一个数组记录算法过程中每一个节点所得的“权重和”最低的N个数字。这样计算得到排名前N的最低票价及对应的列车线路。
Dijkstra 算法的伪代码如下[4~5,7]:
算法 Dijkstra(G,s)
//单起点最短路径的Dijkstra算法
//输入:具有非负权重的加权图G=
//输出:对于V中的每个顶点v来说,从s到v的最短路径长度dv以及路径上的各顶点
Initialize(Q) //将顶点优先队列初始化为空
for V中每一个顶点v do
dv←0;pv←null //pv是最短路径上倒数第2个顶点
Insert(Q,v,dv) //初始化优先队列中顶点的优先级
ds←0;Decrease(Q,s,ds) //将s的优先级更新为ds
VT←Ø
for i←0 to |V|-1 do
u*←DeleteMin(Q) //删除优先级最小的元素

改进的Dijkstra算法可以得到前N名的最短路径,此时需要建一个副表,将每次提取出来的前N名最短路径ds用数组保存下来,得到需要的路径长度后反推该长度对应的路径。
2.4 得到用时最短线路
用时最短路线与最少费用计算稍有不同,转车换乘中间环节的用时必须考虑,需要在上述列车线路网络基础上,考虑在换乘时间的处理。因此需要单独对每个车站进行网络赋权优化处理。
2.4.1 考虑换乘衔接时间的中转方案
在基本网络中,两城市之间使用的车次信息完全与12306官网显示的信息一致。对于一列列车同时穿过多个城市的,只是将连接的站点两两之间建立互通的所有列车信息,每条线赋给车次属性(票价、出发时间、到达时间、运行时间)。
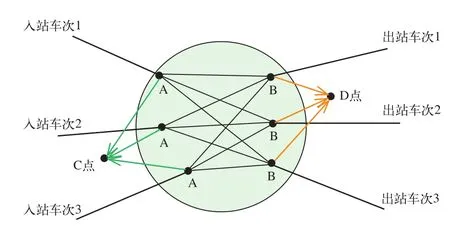
图2 某中转火车站点
与票价最优比选不同的是,时间最短的优化需将网络中每个节点(即车站)做相应的处理。如图2中所示,每个站点到达的列车与在其到站后从该站出发的所有列车之间增加一条“中转时差线”,它的属性为到达列车转到另一辆出发列车的时间差。对于某个站点,到达的列车终点记作该站的A特性点,出站的列车起点记作B特性点。所有A特性点再汇总至一个虚拟结点C,代表作为终点时的该站,A、C之间线段赋值为0;所有B特性点汇总至另一虚拟结点D,代表作为起点时的该站,B、D之间线段赋值为0。当选中站点1和站点2为起止点时,实际是站点1的D点到站点2的C点之间的最短路径问题,此时再用Dijkstra算法或改进的Dijkstra算法获得最短路径或排名前N的最短路径结果。这就充分考虑了中转带来的时间延误。这样得到的用时最短路径也是最合理的。
2.4.2 考虑同城多站的情况
以北京为例,北京市区内有北京站、北京南站、北京西站以及北京北站共4个客运车站,车站之间的换乘就必须考虑一个最小换乘时间,处理方法就是连接4站之间的C属性点到D属性点,并且按照城市内部交通方式附上一个值(此数据可以很容易地在百度地图上获取),同时将此4站汇总到一个公共点O点作为北京的代表,连接线权重赋为0,如图3所示。

图3 同城多站点连接处理示意图
通过以上对站点的简化处理,采用改进的Dijkstra算法[3~6]即可计算出用时最短路径和排名前N的最短路径。当路径选择确定后,只需按选中的车次信息购票。
2.5 路线可靠性评价
不仅是中转换乘,列车晚点导致的延误损失也值得关注。为此,方案中可以开辟空间,根据统计数据对路线进行可靠性评价,计算出线路晚点时间期望值与方差,同时可以通过网络连接调出该线路最近一周的晚点分布图。
3 算法实现
本算法主要提供旅程规划与列车中转方案推荐,面向的出行工具是列车,采用Java语言编写。通过采集铁路系统的相关数据,再根据用户的出行需求,为用户提供最合适的旅行路线。
推荐的旅行路线会根据用户不同需求而不同。比如,用户可以根据自己的需要,选择最短时间为目的、或者最少花费为目的,或者在春运等比较繁忙时,一些路线会比较拥挤甚至无票,可以选择拥挤程度较低而且有票的路线。
算法实现流程如图4所示。
核心程序通过获取用户提出的需求和限制条件,依据铁路系统数据进行计算,给出智能购票推荐方案。使用方法如下。
由用户确定自己的需求:出发地、目的地以及限制条件,限制条件是指希望的票价等级、花费的时间、是否需要在出发地与目的地之间途径某个地方、希望绕开的某条路线等,完成需求输入后,程序自动把规划好的旅途路线反馈给用户,如果用户不满意,还可以更改限制条件重新计算。程序在处理后显示方案时,既用高亮线画出线路图,又给出文字注解,包含车次、用时和车票价格等信息。

图4 推荐算法实现流程
4 计算实例
以2013年9月4日的数据为例。
4.1 有直达车的两站点通行
延安去太原两列车时间和价格如表1。

表1 两列车时间和价格表
这是典型的价格一致时间不同的。在同时能购到两种票的前提下本算法会自动选择前者。
4.2 需要中转换乘的两站点通行
唐山到胶州,有K704(03:56-14:09,历时10:13)和 K1394(19:01-06:29,历时 11:28),硬座票价均为105元,硬卧中铺为190元,如果在铁路官网12306上查询也只能得到这一个结果。但通过本文方案计算,可以发现另一条更加优越的线路——唐山到天津再到胶州,从唐山乘坐T238到天津(05:50-07:04,历时01:14)转D331到达胶州(07:46-11:42),总历时05:52(含中转延误时间),票价合计硬座(二等座)213.5元,硬卧中铺(一等座)324.5元。如果赶时间,无疑后面的方案更有价值。
5 结束语
上述方案利用高效算法,同时考虑换乘时间、晚点、同城多站等因素,能够为用户提供切实可行的铁路出行购票策略。
基于网络分析的铁路路径优化及购票推荐算法,可以为出行者提供更智能更方便的铁路出行选择。目前,各种交通工具相对独立,不能及时有效调配资源,造成资源的浪费,建立综合交通运输体系的协调机制很有必要。基于本文所提出的方法,可以将铁路、公路乃至航空进行整合,形成覆盖全方式的出行路径选择及优化系统。本文提供的方案有助于综合智能交通协同机制的建立,并辅助用户快捷地挑选最优出行方案。
[1] 2013年春运落幕,全国出行人次突破34亿[EB/OL].http://news.xinhuanet.com/local/2013-03/06/c_114917679.htm,2013-03-06.
[2]上海到德阳8张票换乘7次‘换乘哥’[EB/OL].http://china.cnr.cn/yaowen/201302/t20130206_511931498.shtml,2013-02-06.
[3] 胡运全. 运筹学教程[M]. 4版. 北京:清华大学出版社,2012,11:242-245.
[4] 柴登峰,张登荣. 前N条最短路径问题的算法及应用[J].浙江大学学报:工学版,2002,36(5).
[5] 王 峰,游志胜,曼丽春,等. Dijkstra及基于 Dijkstra的前 N条最短路径算法在智能交通系统中的应用[J]. 计算机应用研究,2006(9).
[6] Steven M.LaValle. 规划算法[M]. 张庆雅,孙 东,译.北京:清华大学出版社,2011,1:37-38.
[7] Anany Levitin. 算法设计与分析基础[M]. 潘 彦,译. 北京:清华大学出版社,2007,1:246-249.
