基于星间距离测量的高精度自主导航*

熊 凯，魏春岭，刘良栋

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

0 引言

实现卫星自主导航有助于降低卫星对地面测控的依赖程度，增强卫星系统在紧急情况下的自主生存能力.但是，以目前的技术水平，中高轨卫星缺乏高精度自主绝对导航手段.传统的卫星自主导航方法包括基于光学敏感器的天文导航方法和基于星间链路伪距测量的方法等［1-4］.其中，基于光学敏感器的天文导航受到地心方向测量精度的限制，难以满足卫星高精度自主导航的要求;基于星间链路伪距测量进行导航时存在“亏秩”问题，即仅距离测量情况下不能对星座的整体旋转形成有效的几何约束，造成星座卫星的绝对定位误差随时间增长而逐步积累.

以往研究表明，将卫星轨道动力学方程简化为二体问题处理时，基于星间测距的卫星导航系统是不可观的.如果考虑卫星轨道运动的三体问题，即同时考虑地球和月球引力影响，那么星间测距导航系统是可观的［5-6］.但是，对于参与导航的两颗卫星均为地球卫星的情况，由于月球引力对地球卫星动力学的影响较小，导航系统的可观度较弱，事实上仍然难以实现高精度导航.

为了解决这一问题，可以在地球卫星和月球卫星之间建立星间链路进行导航，此时，两颗卫星的动力学方程分别受到地球和月球引力的显著影响.在这种情况下，导航系统不仅具有可观性，而且具有较高的可观度.此时，基于地球卫星和月球卫星之间的距离测量信息以及三体轨道动力学方程，通过设计适当的扩展卡尔曼滤波(EKF)算法，可以同时估计出地球卫星和月球卫星的绝对位置，实现仅依赖星间测距信息的高精度自主导航.

本文首先介绍基于地-月卫星星间测距的自主导航方法;其次，针对初始位置误差影响导航精度的问题，提出基于“星间测距+紫外导航敏感器”的组合导航方法;最后，通过计算 Cramer-Rao下界(CRLB)和数学仿真分析了所提导航方法的精度.

1 基于星间测距的自主导航

本节介绍星间测距自主导航的基本方法.首先从直观上说明选择1颗地球卫星和1颗月球卫星参与导航的原因.如果选择两颗地球卫星参与导航，可能出现卫星位置不断变化而星间距离不变的情况，此时，卫星位置变化不改变观测量，仅依赖星间测距信息显然无法实现自主导航.相反，如果选择1颗地球卫星和1颗月球卫星参与导航，此时，星间测距示意图如图1所示.

由图1可知，随着卫星位置变化，导航系统能够获得一组独特的星间距离观测量序列.对于处在不同位置上的卫星，所得到的星间距离观测量序列是不同的.星间距离观测量序列中同时包含了地球卫星和月球卫星的绝对位置信息.在获得观测量的基础上，结合卫星三体轨道动力学模型进行滤波处理，能够估计出参与导航的卫星位置.本文将利用CRLB对该方法的可行性作进一步分析.

应当说明，卫星在轨运动符合轨道动力学规律，其位置变化可通过轨道动力学方程来描述.对基于星间测距的自主导航系统而言，除观测量以外，动力学方程也能够提供部分导航信息.采用复杂的动力学方程有助于改善系统的可观性，因此，要求在动力学方程中考虑三体摄动(如月球摄动)的影响.此外，当三体摄动的影响较弱时，其影响会淹没在其他摄动中，不会对导航性能的改善起到实质性作用.因此，如果仅依赖星间测距信息进行自主导航，要求参与导航的卫星中至少有一颗卫星受到三体摄动的显著影响.

下面给出导航方法的数学描述.为了设计导航滤波算法，要求选择适当的状态变量，并建立描述状态变量时间递推关系的状态方程，以及描述状态变量与观测量关系的观测方程.选择参与导航卫星的位置矢量和速度矢量在地心惯性系的3个分量作为状态变量，即

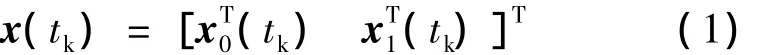
式中，

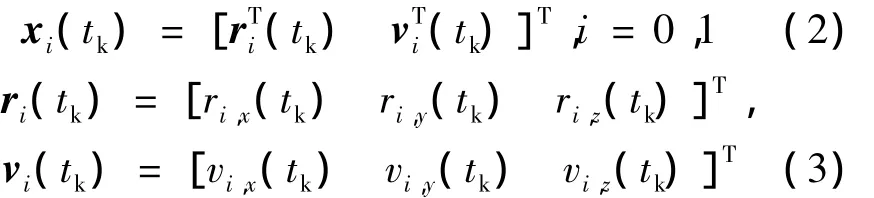
r0(tk)和v0(tk)表示地球卫星的位置矢量和速度矢量，r1(tk)和v1(tk)表示月球卫星的位置矢量和速度矢量，下标i用于区分地球卫星和月球卫星，tk表示时间.

考虑地球的非球形引力摄动和作为三体摄动的月球引力摄动，作为状态方程的卫星轨道动力学方程如下所示:

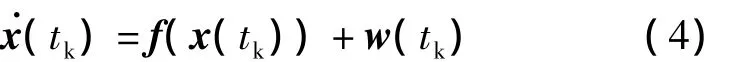
其中，

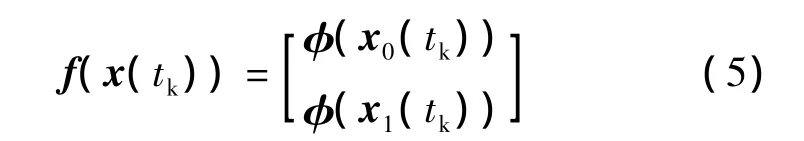
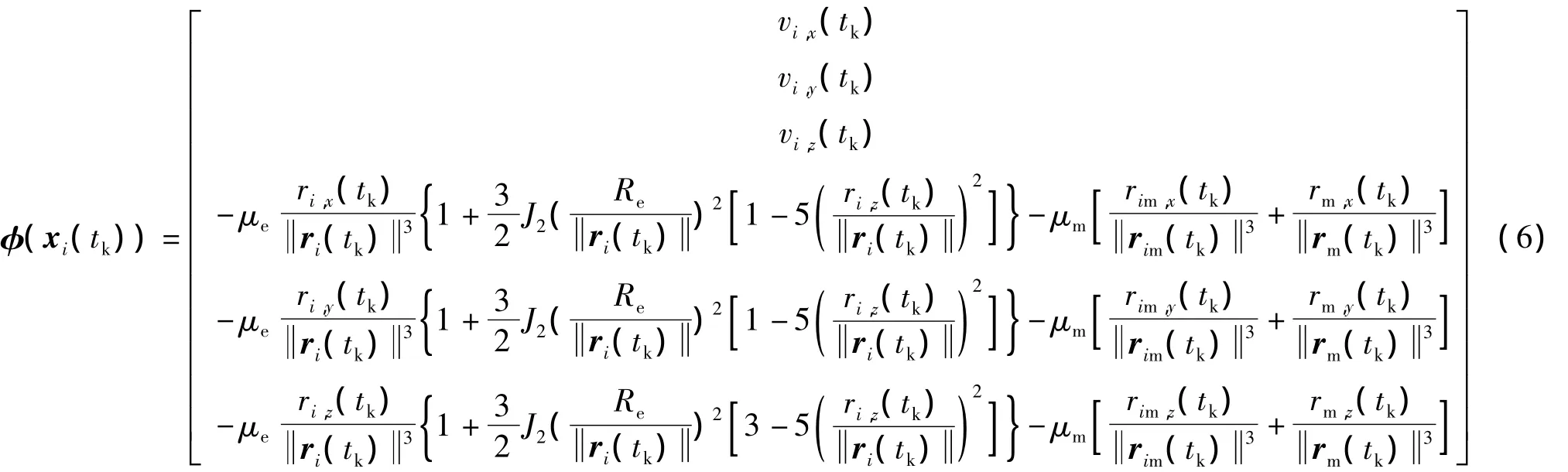
其中，μe是地球引力常数，Re是地球半径，J2是二阶带谐项系数，表示范数，即是月球相对于地心的位置矢量，即rim(tk)=ri(tk)-rm(tk)，μm是月球引力常数，rm(tk)可通过月球星历计算得到.w(tk)表示系统噪声，用来描述未建模的误差项.应当说明，上述简化的轨道动力学模型主要用于EKF算法中雅克比矩阵的推导，实际应用过程中，应采用高精度轨道动力学模型实现地球卫星和月球卫星的轨道外推.

基于星间测距的导航系统测量模型如下所示:

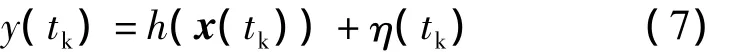
其中，

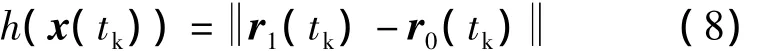
y(tk)是tk时刻地球卫星和月球卫星之间的距离观测量，η(tk)表示测量噪声.

本文采用EKF算法处理星间测距信息，对参与导航的卫星位置和速度进行估计;EKF算法根据状态变量(1)、状态方程(4)和观测方程(7)进行设计.EKF方程可参阅文献［7］.

文献［5］研究了基于星间测距的自主绝对导航方法，要求参与导航的卫星中至少1颗位于地月系拉格朗日L2点，需要通过位置保持控制维持卫星在L2点附近的晕轨道运行.与文献［5］不同，本文所选取的参与导航的卫星分别为地球卫星和月球卫星，采取这一方案的优势在于不需要频繁的对卫星进行位置保持控制.

2 “星间测距+紫外导航敏感器”组合导航

考虑到星间测距信息不直接反映地球卫星和月球卫星的绝对位置，对状态变量的修正作用较弱，较大的初始位置误差导致滤波收敛速度较慢.另外，自主导航系统的状态方程和观测方程都是非线性的，较大的初始位置误差会造成较大的线性化误差，该误差如果得不到及时修正，会随着滤波迭代过程不断积累，从而持续影响估计精度.因此，基于星间测距的自主导航系统易受初始位置误差影响.上述分析与数学仿真结果是一致的.

为了克服初始位置误差的影响，本文提出，融合星间测距信息和紫外导航敏感器的测量信息，建立“星间测距+紫外导航敏感器”组合导航系统.地球圆盘无论在白天或夜间均存在适应于探测的紫外临边辐射的特征，且辐射信号稳定，随经纬度和季节变化很小，随观测方位角变化也很小.这一特征为紫外导航敏感器地心方向测量提供了良好的信号基础.正在研制的紫外导航敏感器采用光机电一体化结构，能同时对地球和恒星成像，集成了地球敏感器和星敏感器的功能［8］.采用紫外导航敏感器可以直接从成像信息中提取导航所需的星光角距观测量，避免导航精度受姿态误差或敏感器安装误差影响.

通过地球卫星上的紫外导航敏感器获得的星光角距观测量是地心方向矢量和恒星方向矢量的夹角，如图2所示.

图2 星光角距观测量Fig.2 Star-Earth angle measurement

图2中，us1是恒星方向矢量是地心方向矢量.紫外导航的主要问题是定位精度受地心方向测量精度的限制，并且，以目前的技术水平，地心方向测量精度很难得到大幅度提升.

将星光角距测量信息引入自主导航系统，能够增强测量信息的修正作用，相当于为星间测距导航提供了中等精度的先验位置信息;在此基础上，基于高精度的星间测距信息，可以实现卫星高精度自主导航.所建立的组合导航系统观测方程可写为如下形式:

式中，

y1(tk)表示组合导航系统的观测量，v1(tk)表示测量噪声，αsj(tk)是星光角距，usj(tk)(j=1，2，…，N)是恒星方向矢量，下标j用于区分不同的恒星.

3 导航系统性能分析

本节利用CRLB分析导航系统的性能.CRLB是根据给定的系统模型、先验信息以及噪声统计特性计算得到的状态估计误差均方差的最小值，CRLB的取值直接反映了一个导航系统的本质特性，可以作为衡量系统可观度大小的指标.如果用于计算CRLB的模型与实际系统相符，那么任何一种滤波算法都不能超越CRLB所规定的估计精度.相对于一般的可观性分析方法，CRLB的优势体现在以下几个方面:首先，借助CRLB不仅能够对线性系统的可观性进行分析，还能对非线性系统的可观性进行分析;其次，利用CRLB不仅能够判断系统是否可观，在系统不可观的情况下，还能辨别出哪些状态变量是不可观的;再次，CRLB不仅能够对可观性进行定性分析，还能进行定量分析，即针对每个状态变量，给出状态估计所能达到的最高精度.关于CRLB的具体计算方法可参阅文献［9］.

考虑两颗卫星参与导航的情况，其中1颗在半长轴为12 275 km，轨道倾角为109.8°的圆轨道上环绕地球运动，另外1颗在半长轴为1 995 km，轨道倾角为90°的圆轨道上环绕月球运动.采用高精度轨道仿真软件模拟产生真实轨道数据，用于计算CRLB，并在下一节用于模拟产生观测数据和评估滤波精度.

首先，对比基于地-月卫星星间测距的自主导航系统和基于“星间测距+紫外导航敏感器”的组合导航系统的性能.假定星间距离测量精度为10 m，星光角距测量精度为0.02°，仿真时间为地球卫星的5个轨道周期，观测数据每1秒更新1次.初始位置误差在1～20 km之间变化时，对应星间测距导航系统和组合导航系统定位误差的CRLB如图3所示.

图3 对应不同初始误差的定位误差方差下界Fig.3 Lower bounds of the position error with different initial errors

显然，星间测距导航系统的性能受到初始位置误差的显著影响，而组合导航系统受初始位置误差的影响不大.如果再考虑初始误差对线性化误差的放大作用，初始误差对星间测距导航性能的影响更严重.

下面对比基于紫外导航敏感器的自主导航系统和基于“星间测距+紫外导航敏感器”的组合导航系统的性能.假定初始位置误差为1 km，星光角距测量精度在 0.01°～0.1°之间变化时，对应紫外导航系统和组合导航系统定位误差的CRLB如图4所示.不难看出，紫外导航精度取决于星光角距测量精度，而组合导航的稳态精度主要取决于星间测距导航的精度.将地-月卫星星间测距与地球卫星上的紫外导航敏感器相结合，所得到的组合导航系统定位精度较高，且受初始误差影响较小.

图4 对应不同测量精度的定位误差方差下界Fig.4 Lower bounds of the position error with different measurement accuracy

4 仿真结果

仿真过程中，采用EKF算法处理根据轨道数据模拟产生的测量数据，同时估计地球卫星和月球卫星的位置速度.假定星间距离测量精度为10 m，星光角距测量精度为0.02°.EKF算法的系统噪声方差阵和测量噪声方差阵分别根据动力学建模误差和测量噪声的幅度选取，初始误差方差阵取为仿真中设置的实际初始误差方差的2倍.假定初始位置误差为10 km，星间测距导航系统和组合导航系统的位置估计误差曲线如图5所示.

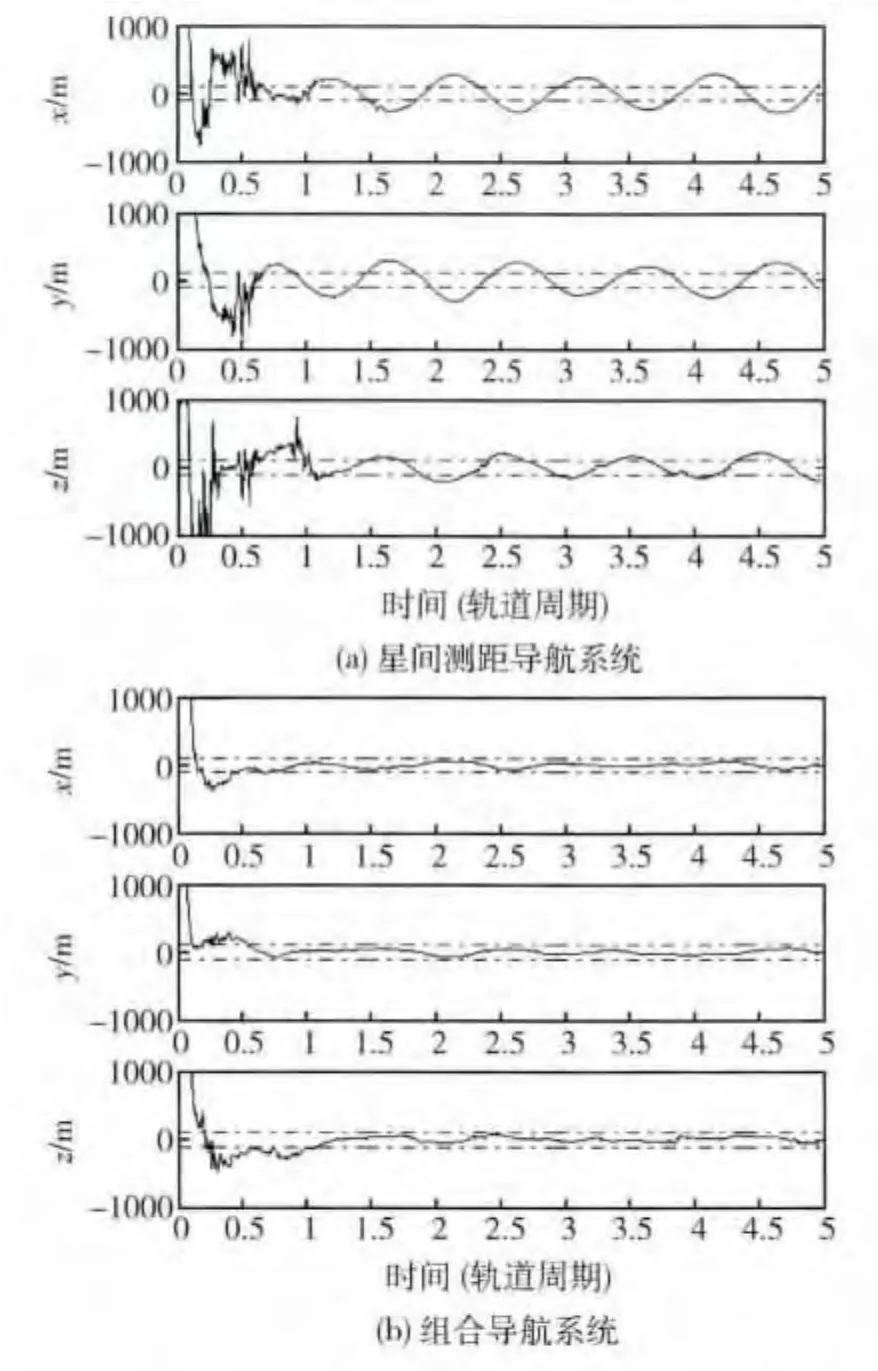
图5 导航系统位置估计误差曲线Fig.5 Position estimation error curves of navigation systems

图5中实线表示位置估计误差曲线，虚线表示100 m的期望定位精度.从图中可以看出，本文所提组合导航方法对初始位置误差不敏感，能够大幅度提高导航精度.应当说明，初始位置误差较小的情况下(1 km)，仅采用地-月卫星星间测距信息也能达到类似的导航精度，这说明星间测距导航性能易受初始位置误差影响的判断是正确的.在相同的条件下，经过蒙特卡罗仿真，星间测距导航、紫外导航和组合导航定位误差均方根的统计值分别为290 m、136 m和64 m.应当说明，月球和地球卫星之间的相对距离测量会存在地球和月球遮挡导致信号中断的问题，并且，远距离测距会导致信号延迟，天体遮挡和信号延迟对滤波器收敛时间和精度的影响还需要进一步仿真分析.

5 结论

本文研究基于地球卫星和月球卫星的星间测距信息同时确定地球卫星和月球卫星绝对位置的自主导航方法.该方法存在导航性能易受初始位置误差影响的问题，在卫星初始位置误差较大的情况下，滤波收敛速度较慢，在卫星的几个轨道周期内难以得到理想的导航精度.针对这一问题，本文将光学导航信息引入卫星自主导航系统，提出“星间测距+紫外导航敏感器”的组合导航方法，紫外导航敏感器的主要作用是提供中等精度的初始位置信息;该方法的优势在于能够显著改善导航滤波器的收敛性，在卫星初始位置误差和星光角距测量误差较大的情况下实现快速导航，取得优于100 m的定位精度.

［1］CHRISTIAN J A，LIGHTSEY E G.Review of options for autonomous cislunar navigation ［J］.Journal of Spacecraft and Rockets，2009，46(5):1023-1036.

［2］FANG J，NING X.Installation direction analysis of star sensors by hybrid condition number［J］.IEEE Transactions on Instrumentation and Measurement，2009，58:3576-3582.

［3］PSIAKI M L.Absolute orbit and gravity determination using relative position measurements between two satellites［J］.Journal of Guidance，Control，and Dynamics，2011，34(5):1285-1297.

［4］苏晓丹.一种通过观测两颗恒星确定飞行器姿态的算法［J］.导航与控制，2009，8(2):22-25.SU X D.An algorithm to determine aircraft attitude through observation of two stars［J］.Navigation and Control，2009，8(2):22-25.

［5］HILL K，BORN G H.Autonomous interplanetary orbit determination using satellite-to-satellite tracking ［J］.Journal of Guidance，Control and Dynamics，2007，30(3):679-686.

［6］HILL K，BORN G H.Autonomous orbit determination from lunar halo orbits using crosslink range［J］.Journal of Spacecraft and Rockets，2008，45(3):548-553.

［7］秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998:185-187.

［8］尉志军，刘晓军.三轴紫外光学成像敏感器［J］.光电工程，2008，35(11):86-90.WEI Z J，LIU X J.Three-axis ultraviolet optical sensor［J］.Opto-Electronic Engineering，2008，35(11):86-90.

［9］ZHANG X，WILLETT P，BAR-SHALOM Y.Dynamic Cramer-Rao bound for target tracking in clutter［J］.IEEE Transactions on Aerospace and Electronic Systems，2005，41(4):1154-1167.