中亚地震目录震级转换及其完整性分析1
2014-05-05冉洪流
吴 果 周 庆 冉洪流
(中国地震局地质研究所,北京 100029)
中亚地震目录震级转换及其完整性分析1
吴 果 周 庆 冉洪流
(中国地震局地质研究所,北京 100029)
为编制能够应用于地震危险性分析的中亚地区统一震级标度为矩震级的地震目录,从国际地震中心(ISC)下载得到该地区1907—2012年的地震数据,该数据包含众多机构不同震级标度的地震记录。以MW,GCMT为参考机构震级标度,并用最小二乘法拟合了其他机构震级标度与MW,GCMT之间的转换关系。在挑选某次地震事件的唯一震级记录时,以对应转换关系的相关系数大且剩余标准差小为准则进行筛选。对于少量没有震级转换关系或者拟合优度过差的地震记录,使用间接转换关系或者全球转换关系予以补充转换。震级转换后,用时空窗法删除前余震,并考虑构造环境和地震活动水平的空间差异性将研究区划分成5个子区域。采用地震记录时间累积曲线法、最大曲率法(MAXC)和拟合优度检验法(GFT)综合分析各个分区的最小完整震级(MC),并在此基础上用极大似然法拟合相应的地震活动性参数。结果表明,每种完整性分析方法各具一定的优缺点,但采用综合分析的方法能够得出最佳的MC。地震记录时间累积曲线法能分析出高质量地震目录的起始时间,以作为后两种方法的基础,但容易受到地震活动水平随时间波动的影响。由于研究区目录质量较差,最大曲率法误差过大以至于只能作为其他方法的补充,拟合优度检验法的GFT参数也普遍只能达到80%左右。GFT最大值点可能并不对应MC,但是MC通常都在GFT极大值点取得。5个分区1964—2012年的MC普遍在MW4.8左右,b值在1.136—1.514之间波动。
矩震级 震级转换 最小完整震级 最大曲率法 拟合优度检验法 极大似然法
引言
地震危险性分析直接为国家重大工程项目提供抗震设计参数,意义十分重大,而地震目录是地震危险性分析的重要基础资料。然而,地震目录往往包含多种震级标度的地震记录,相互之间存在一定的差异,这为地震目录的研究和应用带来了诸多不便(刘瑞丰,2003;陈运泰等,2004;张宏志等,2007)。近年来,国内专家学者根据中国数字地震台网观测报告提供的数据,拟合了我国常用的面波震级(MS)和近震震级(ML)之间的转换关系(张宏志等,2007;汪素云等,2009;2010)。
由于矩震级(MW)具有与地震震源的物理过程直接关联、不会饱和等优点,成为当今国际地震学界推荐优先使用的震级标度(陈运泰等,2004)。国际上最新的衰减关系模型大都以矩震级为震级标度(Power等,2008),同时,美国地震区划图编制过程中用到的空间光滑模型和背景地震模型也是建立在统一震级标度为矩震级的地震目录的基础上(Frankel等,1995;1996;Petersen等,2008;张力方等,2008;潘华等,2009)。因此,对一个地区进行地震活动性和地震危险性研究时,往往需要优先编制该区域统一震级标度为矩震级的地震目录。然而,从国际权威的地震网站上下载得到的地震目录往往包含不同机构的多种震级标度的地震记录,这些震级标度在测定公式和技术规范等方面都存在较大的差异。对此,国际上的学者多通过回归分析,拟合其他震级标度与矩震级之间的经验关系,进而经过震级转换得到统一震级标度为矩震级的地震目录。主体思路分为两种:一种是基于某个区域的地震数据进行回归分析(Johnston,1996;Papazachos等,1997;2002;Baba等,2000;Burton等,2004;Grünthal等,2009;Yadav等,2009;2011;Akkar等,2010;Leptokaropoulos等,2013);另一种是采用全球地震数据进行回归分析(Ekström等,1988;Scordilis,2006;Bormann等,2008)。由于各个地区的震级测定公式和台站的台基响应以及构造背景等存在差异,往往优先采用区域拟合关系。
很多学者在进行震级转换时,往往只简单的拟合一些国际上有影响力的机构震级标度之间的转换关系,而没有考虑某些机构震级标度与选择的参考机构震级标度之间缺少样本或者拟合参数过差等复杂情况(Yadav等,2009;2011)。当同一条地震记录有多个机构的震级标度可供选择时,也缺少挑选准则的论述。本文在这些方面进行了有益的探索,在数据缺乏的情况下较好地实现了地震目录的震级转换。
在完成震级转换的基础上,可以进一步分析地震目录的完整性。考虑到研究区内构造背景以及地震活动性的空间差异性,需要对其进行分区研究。单一的地震目录完整性分析方法往往存在一定的局限性(Wossner等,2005),所以本文采用地震记录时间累积曲线法(Mulargia等,1985;Frankel等,1996;Yadav等,2009;徐伟进等,2012)、最大曲率法和拟合优度检验法(Wiemer等,2000;Woessner等,2005;冯建刚等,2012;郭秋娜等,2012;谢卓娟等,2012)共三种方法综合分析地震目录完整性,并对各种方法的结果进行对比分析。在完整性分析的基础上,采用国际上通用的极大似然法拟合b值(Aki,1965;Weichert,1980;Bender,1983;Marzocchi等,2003),最终得到了可以直接用于地震危险性计算的地震目录和相关地震活动性参数。
1 研究区域简介
本研究源于横跨中亚数国的一条天然气管线的地震区划(图1)。该管线起自土库曼斯坦和乌兹别克斯坦两国交界处,途经乌兹别克斯坦东南角、塔吉克斯坦中西部、吉尔吉斯斯坦西南部,止于中国新疆的乌恰县,线路全长约1000km。一般工程项目需要考虑场点周围150km范围内的地震活动性,而空间光滑模型中的相关距离c一般取50km,3c范围内的点需要参与光滑计算,为了使最外围的点得到合理有效的光滑值,故选取了管线周围300km的范围作为研究区,具体范围为:东经63.06º—78.72º;北纬34.67º—42.53º。
研究区在大地构造上位于印度板块与欧亚板块碰撞形成的西帕米尔构造节及其附属区域,向北延伸至费尔干纳盆地,西北至图兰台地,西南为阿富汗块体东北角,东至塔里木盆地,东北角为东天山(图1)。由于研究区空间跨度大,地震活动性差异明显,本文在拟合地震活动性参数时,根据构造环境的差异、主要活动断层的分布以及地震活动水平的均一性,对研究区进行了简单的分区(图1中Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ共5个子区域)。
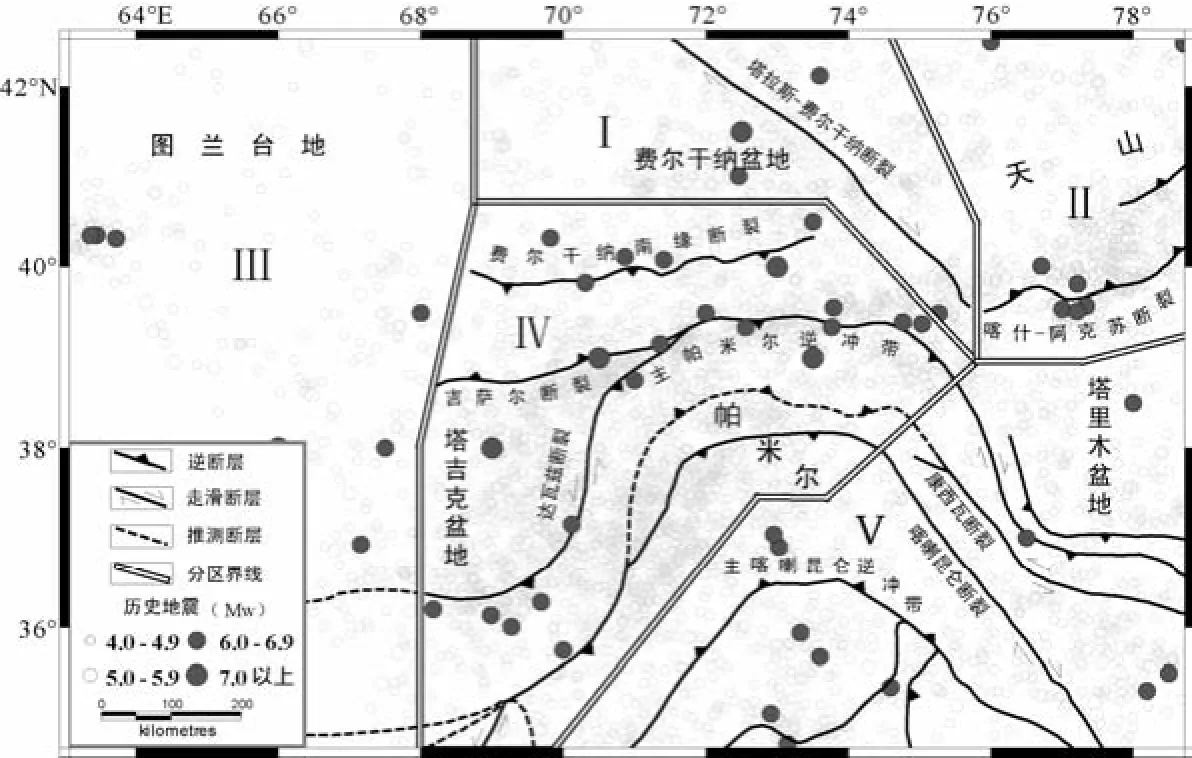
图1 研究区主要活动构造和1907—2012年除丛后MW≥4.0地震分布(根据Robinson等,2007;刘栋梁等,2011;Reiter等,2011编绘)Fig. 1 Map showing major active structures and MW≥4.0 events during period 1907—2012 after de-clustering in the study area (after Robinson et al., 2007; Liu Dongliang et al., 2011; Reiter et al., 2011)
分区Ⅰ对应费尔干纳盆地与东天山之间的走滑断层及其附属区域;分区Ⅱ对应塔里木盆地与东天山之间的逆冲断层及其附属区域;分区Ⅲ以图兰台地为主体,包括阿富汗块体东北角,区内地震活动性较弱;分区Ⅳ位于西帕米尔高原北缘,在印度板块与欧亚板块的碰撞挤压作用下,区内发育一系列大型逆冲断裂带,是研究区内地震活动性最强的区域;分区Ⅴ以西帕米尔高原南缘为主体,包括塔里木盆地西南角部分,区内逆断层和走滑断层都广泛发育,但是地震活动性明显弱于分区Ⅳ。
2 震级转换
2.1 目录来源
本研究所用的地震目录资料来自国际地震中心(International Seismological Centre,简称ISC,United Kingdom,http://www.isc.ac.uk/iscbulletin/search/catalogue/)。国际地震中心的地震目录包含多个国家数十家机构的不同震级标度的地震记录,是目前世界上覆盖面最广、收集最全的地震记录,在地震学家进行地震目录分析时得到了广泛的应用(Burton等,2004;Scordilis,2006;Grünthal等,2009;Yadav等,2009;2011;Leptokaropoulos等,2013)。本文收集到研究区从1907年10月到2013年8月共计53231条地震记录,考虑到震源深度过大的地震对于地面的影响能力极其有限,并且为了避免不同深度的地震在震级转换和完整性分析上可能存在的差异带来的影响,我们只保留了深度小于等于70km的39501条浅源地震记录。目录中各种机构震级标度共有167种,数量排前25位的如表1所示。
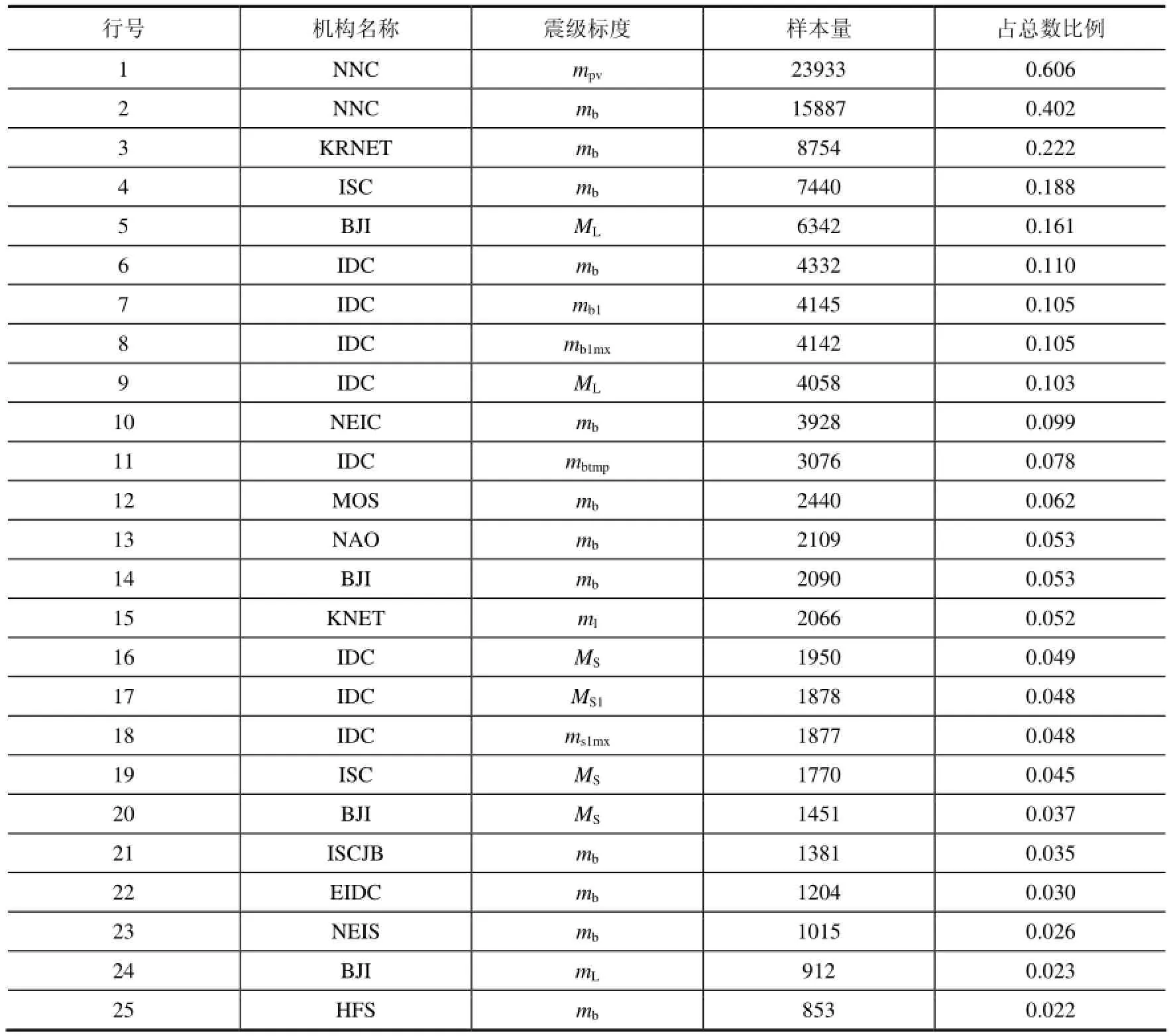
表1 地震目录中样本量前25位的机构震级标度Table 1 Magnitude scales of different institutions with number of recording in the top 25
2.2 参考震级标度
目录中矩震级记录具权威性并且数量最多的为MW,GCMT(Global Centroid Moment Tensor,U.S.A.),所以本研究决定选择MW,GCMT作为参考震级标度。Scordilis(2006)研究发现MW,NEIC(National Earthquake Information Center,U.S.A.)与MW,GCMT接近相同,可以当作同一种数据来使用。所以本文借鉴Leptokaropoulos等(2013)的做法,选择目录中MW,NEIC作为MW,GCMT的补充,进一步加大了参考震级标度的样本量,为了叙述方便,后文一律称为MW,GCMT。

表2 震级转换关系参数表Table 2 Parameters of regression relations between different magnitude scales

续表
2.3 震级转换关系拟合
用最小二乘法分别拟合出其他机构震级标度与MW,GCMT之间的转换关系:

式中,M为原机构震级标度;MW*为参考机构震级标度;a,b为拟合参数。
拟合得到的转换关系参数如表2所示,其中应用次数大于500的拟合图如图2所示。笔者实际拟合的转换关系远多于表2中展示的,但是其中很多关系式在具体转换过程中没有用到,即应用次数为0,这里不予展示。mb,KRNET和ml,KNET数量众多,但是缺少与MW,GCMT存在于相同地震记录的样本,不足以拟合直接转换关系。所以先拟合出二者与ML,BJI之间的转换关系(表2最后两行,图2 h,i),进一步转化为MW,GCMT。
观察表2和图2,可以对各个机构震级标度与参考机构震级标度之间的震级转换关系有一个较为清晰的认识:mpv,NNC(National Nuclear Center,Kazakhstan)与MW,GCMT之间的转换关系应用次数最多,高达20047次,其相关系数为0.757,样本量为69,震级范围为4.3—6.7。该转换关系的相关性水平和样本量在表2所列的所有转换关系中并不算优越,但是由于本研究区包括哈萨克斯坦部分地区,很多中小震数据只在该国有记录,所以在没有更好的选择时只得选用该转换关系。

图2 应用次数≥500的震级转换关系拟合图Fig. 2 Regression relations between different magnitude scales which have been used more than 500 times
ML,BJI(China Earthquake Networks Center,China)与MW,GCMT之间的转换关系应用次数高达11060次,对应的相关系数为0.871,样本量为73,震级范围为4.3—6.9,各方面参数都优于mpv,NNC与MW,GCMT之间的转换关系。该转换关系的大量使用同样是因为本研究区涉及我国西部部分地区,所以中国地震台网中心的地震数据贡献量较大。来自中国地震台网中心的另外几种震级标度,如MS,BJI、MSZ,BJI、mB,BJI、MS7,BJI,与MW,GCMT的转换关系的相关系数都在0.9以上,只有mb,BJI对应的转换关系的相关系数较差,为0.75。观察表2的最后两行可以发现,mb,KRNET(Institute of Seismology,Academy of Sciences of Kyrgyz Republic,Kyrgyzstan)和ml,KNET(Kyrgyz Seismic Network,Kyrgyzstan)与ML,BJI的转换关系的线性程度也非常高,相关系数分别为0.943和0.955。通过以上分析可知,在本研究区内,中国地震台网中心的各种地震记录与MW,GCMT之间存在相当优良的线性关系,这为本文的处理方法在我国境内的适用性提供了一个有力的支撑。

图3 震级转换流程图Fig. 3 The procedure of converting different magnitude scales to a common magnitude scale
2.4 震级转换关系应用准则
目录中一次地震事件往往有多家机构的不同震级标度的震级记录,如何选出其中一种作为该次地震事件的唯一震级记录是震级转换工作必须面对的关键性问题。但是地震学家往往对这一问题不予说明或者缺少论述(Yadav等,2009;2011;Leptokaropoulos等,2013)。为了得到更为精确的震级转换结果,考虑整个转换过程的科学合理性,笔者决定按照一定的准则进行转换工作。如图3所示,优先选择相关系数大并且剩余标准差小的直接震级转换关系,即与MW,GCMT之间的转换关系,这可以减少多次转换带来的不确定性因素的影响。目录中84.3%的地震记录在该过程得以转换。第一步无法如期进行时,拟合研究区的间接震级转换关系,同样优先选择其中相关系数大并且剩余标准差小的关系式。第二步中,14.9%的地震记录得到转换。剩余0.8%的地震记录用全球震级转换关系(Scordilis,2006)予以补充转换。本文拟合的所有转换关系要求满足回归参数下限:相关系数≥0.65,样本量≥25,这可以通过α=0.001的双侧t统计量检验。
经过上述多步处理,我们得到一个属于本研究区的震级全部转化为矩震级,且深度小于等于70km的浅源地震目录。
3 地震目录完整性分析
3.1 完整性分析方法
当人们不了解台站的分布和精度时,往往要通过地震目录来分析最小完整震级(Magnitude of completeness,简称为MC)。MC通常被定义为在一定的时空范围内能够被100%记录到的最低震级(Woessner等,2005)。基于目录的MC分析方法有两类:第一类,夜间噪音干扰减少,台站对低震级地震的记录能力也相应提高,通过对比昼夜间地震发生频度得到MC(Rydelek等,1989;Taylor等,1990);第二类,假设地震发生过程符合自相似假设,那么震级-频度关系(FMD)应当符合G-R关系式(Gutenberg等,1944)。本文使用第二类中应用最普遍的最大曲率法(Maximum curvature,简称为MAXC)和拟合优度检验法(Goodness of fit text,简称为GFT)(Wiemer等,2000;Woessner等,2005)。
由于本文所使用的完整性分析方法是基于地震的主震目录,是一个稳态随机泊松过程的假设,所以在完整性分析之前需要剔除余震(刘杰等,1996;冯建刚等,2012;郭秋娜等,2012;谢卓娟等,2012)。本文所用除丛方法为时空窗法(Utsu,1969;Gardner等,1974;Reasenberg,1985;Uhrhammer,1986)。
最大曲率法是将累积震级-频度关系曲线的曲率最大值点对应的震级作为MC,其对应非累积震级-频度关系曲线的最大频度所在的震级间距(Magnitude bin)。对于渐变型震级-频度关系曲线,最大曲率法求得的MC往往偏低,所以Woessner等(2005)引进了一个修正量,即MC=MC(MAXC)+0.2。
拟合优度检验法最早由Wiemer等(2000)提出,其原理是计算实际观测数据与拟合震级-频度关系之间的差异,以此来衡量理论直线的拟合优度,计算公式如下:

式中,a、b为用极大似然法对假设的最小完整震级Mi以上的数据进行拟合得到的G-R关系中的参数;Bi为实际观测数据的每个震级间距内的地震数;Si为用拟合G-R关系求得的每个震级间距内的地震数。拟合优度参数GFT随Mi的取值而变化,当Mi接近MC时,GFT相应增大。
常用的b值拟合方法有极大似然法(Aki,1965;Weichert,1980;Bender,1983;Utsu,1999;Marzocchi等,2003;Daniel,2007)和最小二乘法。由于最小二乘法在拟合b值过程中缺乏统计稳定性(Page,1968;Bender,1983),国际上学者多使用极大似然法(Wiemer等,2000;Marzocchi等,2003;Woessner等,2005;Yadav等,2009;2011;Leptokaropoulos等,2013),计算公式如下:
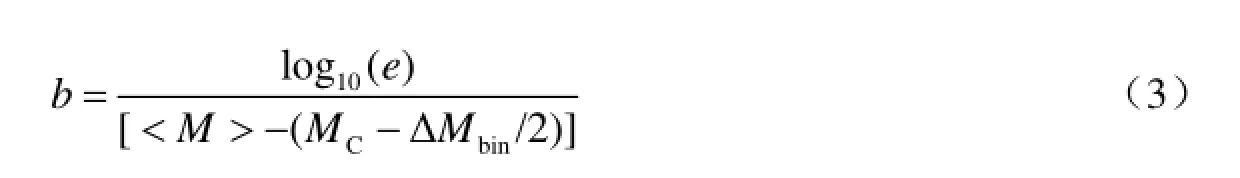
式中,MC为最小完整震级;

由于地震目录的MC是随着时空尺度变化的,我们先做出某个分区的地震记录时间累积曲线(Mulargia等,1985;Frankel等,1996;Yadav等,2009;徐伟进等,2012)。当某时间点出现稳定斜率时,说明该时间点以来某震级以上的地震记录基本是完整的,再用最大曲率法和拟合优度检验法进行详细分析,进而得出某时间段对应的MC。由于不同起始震级的累计地震数相差很大,很难同比例展示在一副图中,所以本文将数量大的累计地震数除以一个系数,这相当于对图中y轴进行一定比例的伸缩,不会影响对曲线线性程度的判断。
为了保证地震危险性分析的合理性和可靠性,最后应用在空间光滑模型和背景地震模型中的地震目录应当包含尽量多的地震记录(Frankel,2007)。所以虽然各个分区不同时间段的MC会有变化,但是本研究倾向于以质量较高的、时间段尽可能长的目录为分析对象。
3.2 分区完整性讨论
分区Ⅰ内的地震目录质量在1965年以后明显提高(图4a),所以选择区内1965—2012年的目录作为完整性分析对象。最大曲率点对应的震级为MW3.3(图4b),而GFT参数最大值在MW4.7处取得(图4c),观察图4a发现,MW3.3以上的地震记录时间累积曲线明显偏离线性,而MW4.7以上的地震记录时间累积曲线具有良好的线性。图4b也显示FMD曲线在MW4.7以上才显示出较好的线性。由以上分析可以确定分区Ⅰ内1965—2012年的地震目录的MC为MW4.7。

图4 分区Ⅰ完整性分析图Fig. 4 Identification of completeness magnitude of zone I
分区Ⅱ内地震目录质量从1964年以来明显提高(图5a),GFT参数存在两个极大值点MW3.5和MW4.7(图5c),同时最大曲率点对应的震级也为MW3.5(图5b)。观察图5a发现,MW3.5对应的地震记录时间累积曲线明显偏离线性,而MW4.7对应的地震记录时间累积曲线具有良好的线性(图5a),结合图5b,可以确定分区Ⅱ内1964—2012年的地震目录的MC为MW4.7。
分区Ⅲ和分区Ⅳ的地震目录质量从1964年以来显著提高(图6a、d),最大曲率点对应的震级分别为MW3.7和MW3.8(图6b、e),但是相应的地震记录时间累积曲线的线性都很差,不能作为完整震级。两个分区的GFT参数分别在MW4.7和MW4.8处取得最大值(图6c、f),其对应的地震记录时间累计曲线和FMD曲线都显示出良好的线性。由此可以确定1964年以来分区Ⅲ和分区Ⅳ的MC分别为MW4.7和MW4.8。
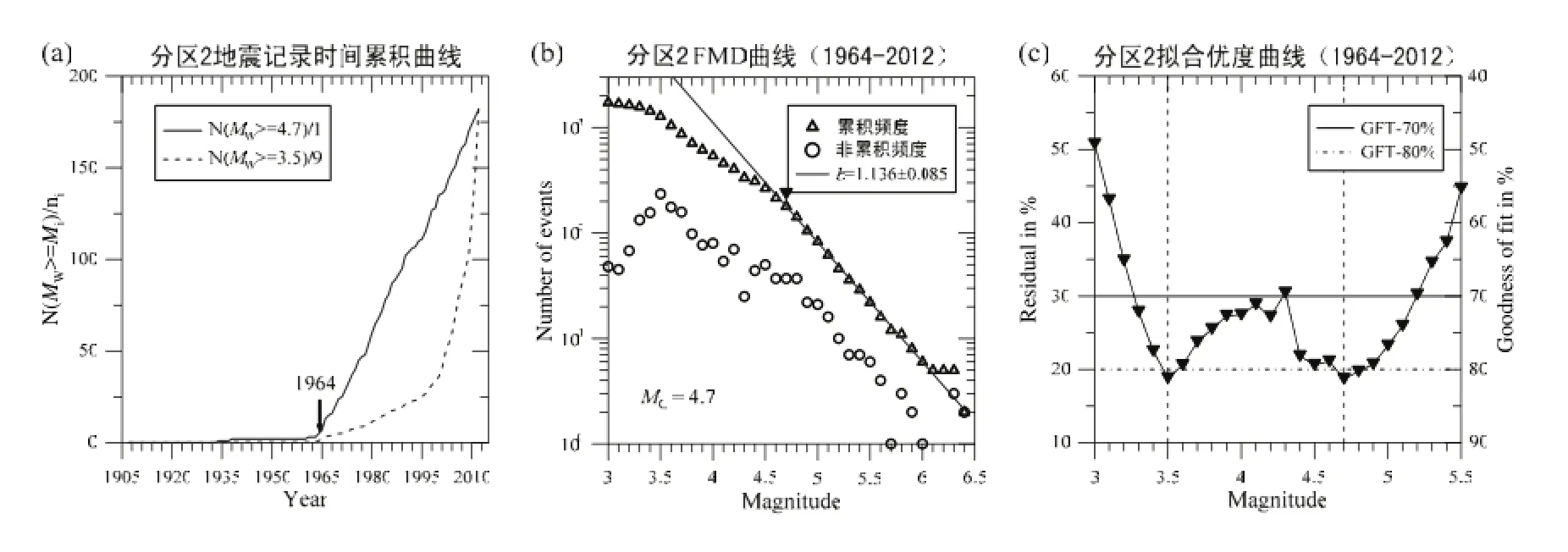
图5 分区Ⅱ完整性分析图Fig. 5 Identification of completeness magnitude of zone II

图6 分区Ⅲ、Ⅳ完整性分析图Fig. 6 Identification of completeness magnitude of zone III and zone IV
分区Ⅴ的地震目录质量同样从1964年以来显著提高(图7a),最大曲率点和GFT参数最大值点对应的震级都为MW4.0(图7b、c),但是MW4.0对应的地震记录时间累积曲线明显缺乏线性(图7a),不能作为完整震级。GFT参数的另一个极大值点在MW4.8处取得(图7c),其对应的地震记录时间累计曲线和FMD曲线都显示出良好的线性,故可确定1964年以来分区Ⅴ的MC为MW4.8。

图7 分区Ⅴ完整性分析图Fig. 7 Identification of completeness magnitude of zone V
根据在完整性分析过程中得到的各个分区的MC,即可用极大似然法求出相应的b值及其标准差,同时笔者也列出了最大曲率点(MAXC)和GFT参数最大值点(MAXG)对应的震级,以便对比分析,结果如表3所示。

表3 分区地震活动性参数Table 3 Seismicity parameters in 5 zones
4 讨论
本文所用的通过回归分析拟合震级转换关系的方法,并没有考虑台站分布、台基响应、震级测定公式等复杂因素,本身存在一定的局限性。但是,为了满足地震区划和工程场地地震安全性评价的需要,这种方法被国际上的学者广泛采用。随着人类积累的地震资料日渐丰富,地震事件的矩震级记录也会增多,这种方法的可靠性也会随之提高。
通过对表2和图2的分析可知,中国地震台网中心(BJI)的多种地震记录与参考震级标度MW,GCMT之间的转换关系都具有很好的线性,相关系数普遍在0.9以上,这说明本文的震级转换方法在我国境内具有很好的应用前景。
观察图4a、图5a和图6d的MW4.7或者MW4.8以上地震记录时间累积曲线发现,这些曲线的斜率都有随时间增加而缓慢减小的趋势,这与整个研究区随着时间向后推移,MW4.8以上的地震减少,而小震增多有关。统计发现,研究区内1965—1988年MW4.8以上地震记录为623条,而1989—2012年MW4.8以上地震记录只有535条,这种地震活动水平随时间的波动性在各个分区不同程度的体现,即会出现上述情况。这也说明,如果采用单一的地震记录时间累积曲线法判断地震目录的完整性,容易受到地震活动水平随时间波动的影响,求得的完整震级和完整年限都有可能出现一定的偏差。
通过观察地震记录时间累积曲线,可以对地震目录质量随时间的变化有清晰的认识,从而得到高质量地震目录的起始年限。而最大曲率法和拟合优度检验法是建立在假设已经知道高质量地震目录起始年限的基础上(Wiemer等,2000),每次都只能选择一个时间段的目录进行分析。所以笔者认为地震记录时间累积曲线法可以作为后两种方法的基础和前提。
在本研究中,最大曲率法求得的MC(MAXC)都明显偏小,以至于失去适用性。分区Ⅰ和分区Ⅱ的FMD曲线呈现出明显的分段性,前后两段都接近线性,但是斜率存在较大的差异,笔者将其称之为“折线型”(图4b、图5b)。“折线型”FMD曲线中,MC(MAXC)偏低1.2至1.4个震级单位(表3),对应的非累积震级-频度关系曲线也呈现出相应的分段性。分区Ⅲ和分区Ⅳ的FMD曲线属于Woessner等(2005)所描述的“渐变型”(图b、e),MC(MAXC)偏低1.0个震级单位(表3)。“渐变型”FMD曲线对应的非累积震级-频度关系曲线没有明显的单峰(频度最大值点),而是呈“大圆弧型”。分区Ⅴ的FMD曲线存在较为明显的曲率最大值点,对应的非累积震级-频度关系曲线也存在较明显的“小圆弧型”单峰(图7b),但是与欧美国家的地震数据拟合的结果相比仍然有较大差距(Wiemer等,2000;Woessner等,2005;Leptokaropoulos等,2013)。分区Ⅴ的MC(MAXC)比真实MC小0.8个震级单位(表3),如果附上Woessner等(2005)所提出的0.2个震级单位的校正,仍然相差0.6个震级单位。同时可以发现,随着累积震级-频度曲线的最大曲率点的明显程度不断增高,对应的MC(MAXC)与真实MC之间的偏差在不断的缩小。
分析最大曲率法误差过大的原因:第一,本研究区域的台网密度和地震记录水平与欧美国家相比存在较大差距,中小震记录缺失尤为严重;第二,研究区内地震活动水平随时间的波动性,进一步放大了最大曲率法的不稳定性;第三,本研究为了考虑分析结果在地震危险性分析中的适用性,在保证地震目录质量具有较高水平的前提下,选择了时间段尽可能长的地震目录作为分析对象;第四,最大曲率法本身的适用条件比较苛刻,只有当FMD曲线有非常明显的最大曲率点时才能得出较为准确的MC。
拟合优度检验法自身存在一定的缺陷,真实目录的GFT参数很难达到90%或者95%的标准(Wiemer等,2000)。其次,选择不同的GFT标准则会求得不同的MC(Leptokaropoulos等,2013)。由于本研究区内地震目录质量较差、地震活动水平随时间具有一定波动性等复杂原因,GFT普遍只能达到80%左右,并且GFT最大值点可能并不对应最佳的MC(表3),需要借助其他方法的配合才能得到准确的结论。但是MC通常都在GFT极大值点取得。
5 结论
本文的研究分前后两个部分,首先通过震级转换得到统一震级标度为矩震级的地震目录,然后在此基础上分析地震目录的完整性,进而拟合出相应的地震活动性参数。这两步工作是地震活动性研究的基础性工作,同时也为地震危险性分析提供基本数据资料,意义十分重大。
在震级转换过程中,由于研究区地跨中亚多国,地震目录的质量与北美和欧洲相比存在较大差距,在拟合震级转换关系时多存在数据不足或者回归参数较差等复杂情况。在挑选某次地震事件的唯一震级记录时,本研究用程序自动对比各个震级记录对应转换关系的拟合优度,以相关系数大并且剩余标准差小为准则进行筛选,再用间接转换关系或者全球转换关系予以补充,很好地完成了震级转换工作。
本文采用的震级转换方法未考虑震级测定公式、台基响应等复杂因素的影响,本身具有一定局限性。但该方法能为地震危险性分析提供必要的数据资料,因此在国际上被广为采用,对于我国的地震安评工作也具有一定的借鉴意义。
完成震级转换后,用时空窗法除丛得到主震目录。进一步对研究区进行分区,在各个子区域上采用地震记录时间累积曲线法、最大曲率法和拟合优度检验法共三种方法综合分析地震目录完整性,并对各种方法的结果进行对比分析。研究发现:
(1)地震记录时间累积曲线法能够分析出高质量地震目录的起始年限,这为使用最大曲率法和拟合优度检验法做进一步的分析提供了基础,但是其自身容易受到地震活动水平随时间波动的影响。
(2)由于地震目录质量较差、地震活动水平随时间波动等复杂原因,最大曲率法求得的最小完整震级明显偏小,误差远超过Woessner等(2005)所提出的0.2个震级单位的修正量。笔者建议只有当震级-频度曲线具有明显的最大曲率点时再使用该方法。
(3)在本研究区,拟合优度检验法的GFT参数普遍只能达到80%左右,并且最大值点可能并不对应最小完整震级,但是最小完整震级通常在GFT参数极大值点取得。
(4)采用多种方法综合分析地震目录完整性的策略,可以弥补单一方法的不足,得到相对合理的最小完整震级。
最后,在完整性分析的基础上用国际上通用的极大似然法求取b值,得到了可以直接用于地震危险性计算的地震目录和相关地震活动性参数。
陈运泰,刘瑞丰,2004.地震的震级.地震地磁观测与研究,25(6):1—12.
冯建刚,蒋长胜,韩立波,陈继峰,2012.甘肃测震台网监测能力及地震目录完整性分析.地震学报,34(5):646—658.
郭秋娜,吕晓健,高战武,2012.汾渭地震带区域地震目录最小完整震级分析.震灾防御技术,7(1):54—63.
刘杰,陈棋福,陈顒,1996.华北地区地震目录完全性分析.地震,16(1):59—67.
刘瑞丰,2003.地震参数.北京:地震出版社,7—15.
刘栋梁,李海兵,潘家伟,Luce C.M.,裴军令,孙知明,司家亮,许伟,2011.帕米尔东北缘—西昆仑的构造地貌及其构造意义.岩石学报,27(11):3499—3512.
潘华,高孟潭,李金臣,2009.新版美国地震区划图源及其参数模型的分析与评述.震灾防御技术,4(2):131—140.
徐伟进,高孟潭,2012.以空间光滑的地震活动性模型为空间分布函数的地震危险性分析方法.地震学报,34(4):526—536.
谢卓娟,吕悦军,彭艳菊,张力方,2012.东北地震区小震资料完整性分析及其对地震活动性参数的影响研究.中国地震,28(3):256—265.
汪素云,俞言祥,2009.震级转换关系及其对地震活动性参数的影响研究.震灾防御技术,4(2):141—149.
汪素云,王健,俞言祥,吴清,高阿甲,高孟潭,2010.基于中国地震台网观测报告的ML与MS经验关系.中国地震,26(1):14—22.
张宏志,刁桂苓,赵明淳,王勤彩,张骁,黄媛,2007.不同标度震级关系和台基影响问题探讨.中国地震,23(2):141—146.
张力方,吕悦军,彭艳菊,谢桌娟,2008.用空间光滑方法评估弱地震活动区的地震活动性参数.震灾防御技术,3(1):27—36.
Aki K.,1965.Maximum likelihood estimate of b in the formula logN=a−bM and its confidence limits. Bull. Earthq. Res.Inst.Tokyo Univ.,43(2):237—239.
Akkar S.,Çağnan Z.,Yenier E.,Erdoğan Ö.,Sandikkaya M.A.,Gülkan P.,2010.The recently compiled Turkish strong motion database:Preliminary investigation for seismological parameters.J.Seism.,14(3):457—479.
Bender B.,1983.Maximum likelihood estimation of b-values for magnitude grouped data.Bull.Seism.Soc.Amer.,73(3):831—851.
Baba A.B.,Papadimitiou E.E.,Papazachos B.C.,Papaioannou C.A.,Karakostas B.G..,2000.Unified local magnitude scale for earthquakes of south Balkan area.Pure Appl.Geophys,157(5):765—783.
Burton P.W,Xu Y.,Qin C.,Tselentis G.,Sokos E.,2004.A catalogue of seismicity in Greece and the adjacent areas for the twentieth century.Tectonophysics,390(1-4):117—127.
Bormann P.,Saul J.,2008.The new IASPEI standard broadband magnitude mB.Seism.Res.Lett.,79(5):698—705.
Daniel A.,2007.Applying a change-point detection method on frequency-magnitude distributions. Bull. Seism. Soc. Amer.,97(5):1742—1749.
Ekström G.,Dziewonski A.M.,1988.Evidence of bias in estimation of earthquake size.Nature,332:319—323.
Frankel A.D.,1995.Mapping seismic hazard in the Central and Eastern United States.Seism.Res.Lett.,66(4):8—21.
Frankel A.D.,Mueller C.,Barnhard T.,Perkins D.,Leyendecker E.,Dickman N.,Hanson S.,Hopper M.,1996.National Seismic Hazard Maps Documentation June 1996.Denver:US Geol.Surv.Open-File Rept.,96—532.
Frankel A.D.,2007.Preliminary documentation for the 2007 update of the United States National Seismic Hazard Maps.Denver:US Geol.Surv.Open-File Rept.,02–420:2—110.
Gardner J.K.,Knopoff L.,1974.Is the sequence of earthquakes in southern California,with aftershocks removed,Poissonian.Bull.Seism.Soc.Amer.,64(5):1363—1367.
Gutenberg R.,Richter C.F.,1944.Frequency of earthquakes in California.Bull.Seism.Soc.Amer.,34(4):185—188.
Grünthal G.,Wahlström R.,Stromeyer D.,2009.The unified catalog of earthquakes in central,northern,and northwestern Europe(CENEC)—updated and expanded to the last millennium.J.Seism.,13(4):517—541.
Johnston A.C.,1996.Seismic moment assessment of earthquakes in stable continental regions—I.Instrumental seismology.Geophys J.Int.,124(2):381—414.
Leptokaropoulos K.M.,Karakostas V.G.,Papadimitriou E.E.,Adamaki A.K.,Tan O.,İnan S.,2013.A homogeneous earthquake catalog for western Turkey and magnitude of completeness determination.Bull.Seism.Soc.Amer.,103(5):2739—2751.
Mulargia F.,Tinti S.,1985.Seismic sample areas defined from incomplete catalogs:An application to the Italian territory.Physics of the Earth and Planetary Interiors,40(4):273—300.
Marzocchi W.,Sandri L.,2003.A review and new insights on the estimation of the b-value and its uncertainty.Annals of Geophysics,46(6):1271—1282.
Page R.,1968.Aftershocks and microaftershocks of the Great Alaska earthquake of 1964,Bull.Seism.Soc.Amer.,58(3):1131—1168.
Papazachos B.C.,Kiratzi A.A.,Karakostas B.G.,1997.Toward a homogeneous moment-magnitude determination for earthquakes in Greece and surrounding area.Bull.Seism.Soc.Amer.,87(2):474—483.
Papazachos B.C.,Karakostas V.G.,Kiratzi A.A.,Margaris B.N.,Papazachos C.B.,Scordilis E.M.,2002.Uncertainties in the estimation of earthquake magnitudes in Greece.J.Seism.,6(4):557—570.
Power M.,Chiou B.,Abrahamson N.,Bozorgnia Y.,Shantz T.,Roblee C.,2008.An overview of the NGA project.Earthquake Spectra,24(1):3—21.
Petersen M.D.,Frankel A.D.,Harmsen S.C.,Mueller C.S.,Hailer K.M.,Wheeler R.L.,Wesson R.L.,Zeng Y.H.,Boyd O.S.,Perkins D.M.,Luco N.,Field E.H.,Wills C.J.,Rukstales K.S.,2008.Documentation for the 2008 Update of the United States National Seismic Hazard Maps.Denver:US Geol.Surv.Open-File Rept 2008-1128,4—39.
Reasenberg,1985.Sencond-order moment of Califonia seismicity,1969-1982.Journal of Geophysical Research,90(B7):5479—5495.
Rydelek P.A.,Sacks I.S.,1989.Testing the completeness of earthquake catalogs and the hypothesis of self-similarity.Nature,337:251—253.
Robinson A.C.,Yin A.,Manning C.E.,Harrison T.M.,Shuan-Hong Z.and Xiao-Feng W.,2007.Cenozoic evolution of the eastern Pamir:Implications for strain-accommodation mechanisms at the western end of the Himalayan-Tibetan orogen.Geological Society of America Bulletin,119(7-8):882—896.
Reiter K.,Kukowski N.,Ratschbacher L.,2011.The interaction of two indenters in analogue experiments and implications for curved fold-and-thrust belts.Earth and Planetary Science Letters,302(2011):132—146.
Scordilis E.M.,2006.Empirical global relations converting MSand mb to moment magnitude.J.Seism.,10(2):225—236.
Taylor D.W.A.,Snoke J.A.,Sacks I.S.,Takanami T.,1990.Non-linear frequency-magnitude relationship for the Hokkaido corner,Japan.Bull.Seism.Soc.Amer.,80(2):340—353.
Utsu T.,1969.Aftershocks and earthquake statistics(I)—some parameters which characterize an aftershock sequence and their interrelations.Journal of the Faculty of Science,Hokkaido University.Series 7,Geophysics,3(3):129—195.
Uhrhammer R.A.,1986.Characteristics of northern and central California seismicity.Earthquake Notes,57(1),21(abstract).
Utsu T.,1999.Representation and analysis of the earthquake size distribution:a historical review and some new approaches.Pure Appl.Geophys,155:509—535.
Weichert D.H.,1980.Estimation of the earthquake recurrence parameters for unequal observation periods for different magnitudes.Bull.Seism.Soc.Amer.,70(4):1337—1346.
Wiemer S.,Wyss M.,2000.Minimum magnitude of complete reporting in earthquake catalogs:Examples from Alaska,the western United States,and Japan.Bull.Seism.Soc.Amer.,90(4):859—869.
Woessner J.,Wiemer S.,2005.Assessing the quality of earthquake catalogs:Estimating the magnitude of completeness and its uncertainty.Bull.Seism.Soc.Amer.,95(2):684—698.
Yadav R.B.S.,Bormann P.,Rastogi B.K.,Das M.C.,Chopra S.,2009.A homogeneous and complete earthquakecatalog for northeast India and the adjoining region.Seismol.Res.Lett.,80(4):609—627.
Yadav R.B.S.,Bayrak Y.,Tripathi J.N.,Chopra S.,Singh A.P.,Bayrak E.,2011.A probabilistic assessment of earthquake hazard parameters in NW Himalaya and the Adjoing Regions.Pure Appl.Geophys,169(9):1619—1639.
Magnitude Conversion of Earthquake Catalog in Central Asia and the Completeness Analysis
Wu Guo, Zhou Qing and Ran Hongliu
(Institute of Geology, China Earthquake Administration, Beijing 100029, China)
In order to compile a homogeneous catalog in moment magnitude for central Asia which can be used in seismic hazard analysis, we downloaded the seismic data during period 1907—2012 from the International Seismological Center (ISC). The earthquake magnitudes of the data are reported in different scales and come from a variety of sources.In this study we take MW,GCMTas the reference magnitude, then derive a host of empirical relationships between magnitude scales from other institutions with MW,GCMTthrough least squares technique. The process, for choosing magnitude scale to a seismic event, follows a rule that giving priority to the one with larger correlation coefficient and smaller residual standard deviation in relevant regression relationship. Indirect conversion relationships and relationships derived from global seismic data serve as supplement when lack of direct conversion relations or the level of goodness of fit is too poor. A spatial and temporal windowing method is applied to remove pre-aftershocks, then the study area is divided into 5 smaller zones on the basis of spatial difference in structural setting and seismic activity. The identification of completeness magnitude (MC) for each zone is done by the combination of three kinds of methods: cumulative number of earthquakes plotted against time, maximum curvature (MAXC) and goodness of fit text (GFT). The seismicity parameters of zones are calculated with maximum likelihood method on the basis of completeness analysis of catalog at last. Results indicate that though each method has its own advantage and drawbacks, we can acquire optimum MCwhen used in combination with other methods. Graph between time and cumulative number of earthquakes can be used to identify the starting time of high-quality catalog, which is the basis of the MAXC and GFT, but it could be easily affected by seismicity fluctuations over time. Because of poor data quality in the study region, the error of MAXC is so big that it can only be used as supplement for two other methods and the fit-level of GFT can only be as large as approximately 80% in zones. Although the maximum of GFT may not correspond to MC, it can be always obtained from extreme point of GFT. The MCof 5 zones during the period of 1964—2012 generally occurs around MW4.8, and the b value varies from 1.136 to 1.514.
Moment magnitude; Magnitude scales transformation; Completeness magnitude; Maximum curvature; Goodness of fit text; Maximum likelihood
吴果,周庆,冉洪流,2014.中亚地震目录震级转换及其完整性分析.震灾防御技术,9(3):368—383.
10.11899/zzfy20140304
国家科技支撑计划课题“特大地震危险区识别及危险性评价方法研究(2010BAK15B01)”;地震行业科研专项“地震安全性评价分类、关键技术指标确定及国家标准修订研究(201408002)”
2014-02-15
吴果,男,生于1988年。2011年毕业于合肥工业大学,现在中国地震局地质研究所攻读硕士学位,现已转为博士阶段。主要研究方向为地震危险性分析。E-mail:wgfirst@foxmail.com
