多模型方法下的地区常住人口规模预测分析——以湖南省株洲市为例

宋汉杰

（湖南师范大学资源与环境科学学院，湖南长沙410081）

多模型方法下的地区常住人口规模预测分析
——以湖南省株洲市为例

宋汉杰

（湖南师范大学资源与环境科学学院，湖南长沙410081）

以1993—2012年湖南省株洲市的常住人口数量为样本数据，对株洲市常住人口数据变化情况进行分析，并分别采用一元线性回归法、二次指数平滑法、GM（1,1）模型预测法，对2013—2020年株洲市的常住人口数据进行预测，得出了株洲市未来8年的常住人口增长预测数据。根据预测结果，为株洲市未来应对常住人口增长的问题提出相关建议。

株洲市常住人口；人口规模预测；一元线性回归法；二次指数平滑法；GM（1,1）模型法

0 引言

人口是一个地区发展最重要的基础，人口的多少与质量直接关系到所在地区的经济水平、生活质量以及未来的发展潜力[1]。人口、资源、环境三者相互影响、相互制约，人口规模的增减会直接影响地区的资源消耗与环境保护这两项指标水平的高低[2]。湖南省株洲市是长株潭“两型示范区”的重要组成部分，准确把握人口增长的规模，可以有效地指导株洲市的资源节约、环境保护等工作。到目前为止，还没有人通过数学模型对整个株洲市的人口发展做出全面科学的预测。因此，依托数学模型对株洲地区的人口的预测，对指导株洲市未来的发展、建设具有重要意义。

地区的人口统计总量可分为：年末总人口、户籍人口、常住人口等。株洲市是中南地区重要的交通枢纽和中转中心，流动人口较多，为了能够准确地统计株洲地区的人口变化，采用排除了流动人口，以地区长期居住的人口为准的“常住人口”作为预测对象。

人口预测的方法有许多种，主要包括：马尔萨斯人口预测法、平均增长法、指数平滑法、自然增长法、一元线性回归预测法、Logistic 模型预测法、GM（1,1）灰色模型预测法等[3]。由于近年来株洲市人口增长速度较为平稳，但人口年均增长率不一致，导致人口增长略有波动。同时，为了提高预测结果的精度、综合应用多模型方法较为合适。因此，本文从株洲市实际出发，分别采用：一元线性回归法、二次指数平滑法以及灰色GM（1,1）模型法3种预测方法。利用1993—2012年的常住人口数据，对株洲市下一个规划期（2020年）之前的未来8年的常住人口规模作出科学的预测，并综合考虑这3种方法的结果，得出未来株洲市人口发展的预测数值，为株洲市在接下来的8年“两型社会”建设以及规划建设提供指导。

1 株洲市人口现状分析

1.1 区域概况

株洲市地处湖南省东北部，罗霄山脉以西，湘江下游，地理位置范围在26°03’～ 28°01’N，112°57’～ 114°07’E之间。整体地势东南高、西北低，地形以丘陵、山地为主，平原、谷地多沿河流分布。气候属亚热带季风性湿润气候，四季分明，年平均气温在18 ℃左右，年均降水量为1400～1700mm。株洲市包括：荷塘区、芦淞区、石峰区、天元区、云龙示范新区、醴陵市、株洲县、攸县、茶陵县、炎陵县共10个县市区。全市土地面积为11248km2。到2012年株洲市常住人口为390.66万，其中城镇人口230.88万，农村人口159.78万，城镇化率为59.1%。株洲市是湖南省“长株潭城市群”的重要组成部分。近几年来，随着国家“中部崛起”和湖南省“一带一部”战略的影响，作为铁路和公路交通枢纽的株洲市，其连接东西部的中转站优势开始凸显，区位的重要性进一步提升。

1.21993 —2012年株洲市常住人口变化分析

在20世纪90年代，株洲市是重要的工业城市，也是中南地区重要的铁路枢纽。进入新世纪后，逐步发展转型，同时，在这段时间内由于受到经济、政策、行政区划变动等因素的影响，株洲市常住人口总量稳步上升。根据《株洲市统计年鉴》1993—2012年人口资料数据，可得如图1所示的人口数量变化趋势图。

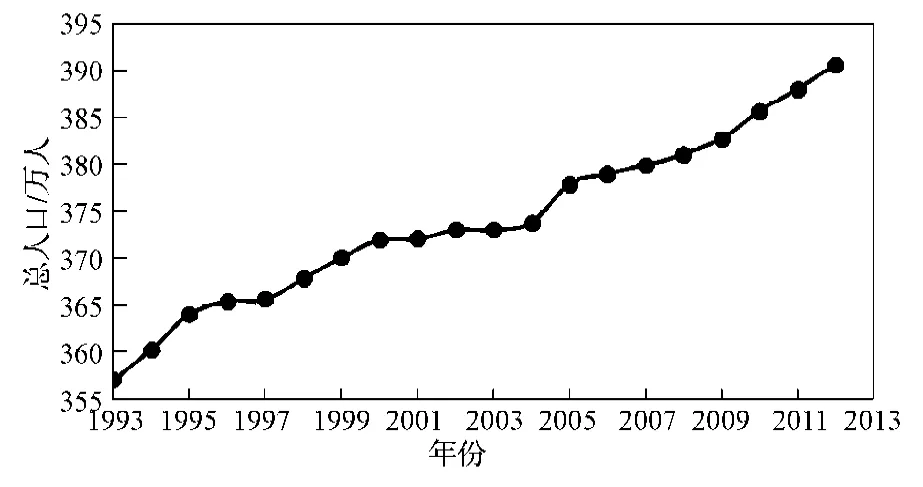
图11993 —2012年株洲市常住人口数量变化图Fig.1The permanent population variation from 1993—2012 in Zhuzhou City

由图1可知，株洲市常住人口在不断增长的大趋势下，大致经历了3个不同的发展阶段[4]。

1）1993—1997年，是株洲市常住人口总量增长的第一个阶段。在这个阶段内，由于受到河西新区的开发，行政区划调整，以及国企改制等经济政策调整的影响，4年里，株洲市常住人口数量显著上升。从1993年的357.05万人，到1995年的364.03万人，年平均增长3.49万人；从1995年之后增长速度下滑，年平均增长仅为0.81万人，至1997年达到了365.65万人。

2）1997—2004年，随着株洲市1997年的一次重大行政区划调整，株洲市的高新技术产业开发区和天元新区先后成立，市区面积进一步扩大，外来迁入人口进一步增长。株洲市常住人口总量从1997年的365.65万人，至2004年增长到373.84万人。

3）2004—2012年，这段时期由于受国家提出“中部崛起”大战略的影响，株洲市的经济建设、对外开放力度不断加强，吸引了更多外来人口的迁入，人口自然增长率也有了显著上升，导致株洲市常住人口总量快速增加。特别是在2007年“长株潭两型示范区”成立后，株洲市的居住环境得到改善，基础设施进一步完善，使株洲市的迁入人口和自然增长率都大幅上升，到2012年为止常住人口已经达到了390.66万人，市区常住人口更是突破了100万大关。

2 2013—2020年人口数据预测

2.1 一元线性回归法

一元线性回归法是一种较简易和方便的人口预测方法，它比较适应于人口增长呈平稳的上升或下降的情况。从图1中1993—2012年的常住人口增长情况来看，株洲市常住人口呈稳定上升的趋势，因此，可以使用一元线性回归方程来进行预测[5]。

2.1.1 一元线性回归方程的建立

本文收集了1993—2012年株洲市人口的具体数据，见表1。

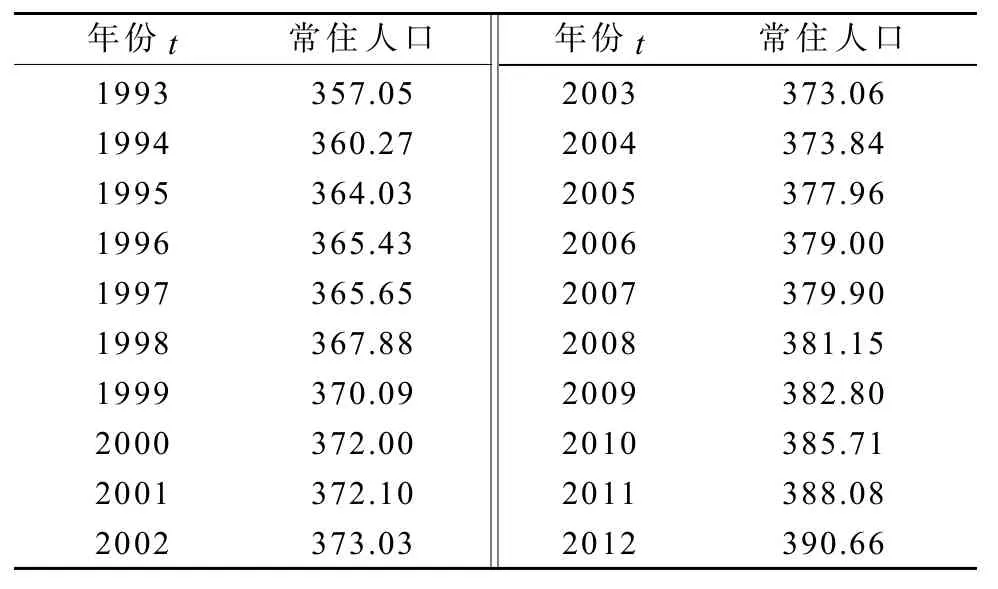
表1 株洲市1993—2012年常住人口实际数据Table1The actual data of permanent resident population in Zhuzhou City from 1993—2012万人

采用SPSS软件对表1中的数据进行Pearson计算，可得出年份与总人口的相关系数为0.989，双侧显著性为0，证明两组数据高度正相关。利用EXCEL软件作出常住人口与年份关系的散点图，并拟合出散点图的趋势线。散点图和拟合情况见图2，其中虚线为趋势线。

图21993 —2012年株洲市常住人口与年份关系散点图Fig.2The relationship scatter plot of the year and the permanent population in Zhuzhou City in 1993—2012

由图2可知，趋势线和人口数据散点的拟合程度很高，这说明年份与总人口呈明显的线性相关性。因此，可以通过构建一元线性回归模型对株洲市未来的人口进行预测，根据1993—2012年株洲市人口数据，构建一元线性回归模型：

式中：Y是常住人口；t是年份；a, b是待定系数。

通过最小二乘法（OLS）可以求得a, b的值：

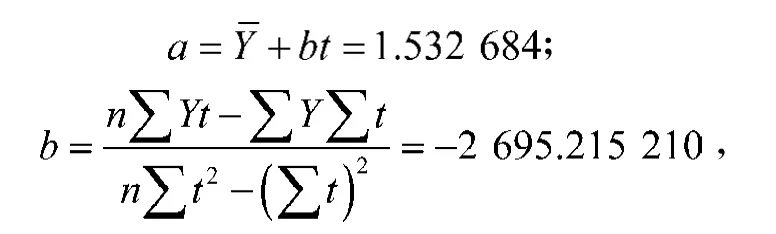
式中n为样本容量，且n=20。

将a, b的值代入式（1），可得一元线性预测模型的方程为

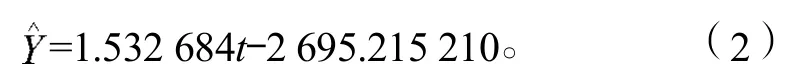
2.1.2 一元线性模型的检验及预测

为了验证模型（2）预测的可行性，必须对其进行检验。采用统计软件EXCEL对方程（2）进行回归分析，可以得出模型（2）的可决系数R2=0.9778，可见回归模型和实际数据的拟合程度相当高。同时，采用EXCEL对模型进行拟合，并对模型进行t检验和F检验，可得检验值t=28.185，|t|＞t0.02518=2.101，F=794.396大于其临界值4.410。对方程（2）的t, F检验表明，它是显著有效的，可以用于株洲市常住人口变化的预测。将年份t带入方程（2）可得2013—2020年株洲市的常住人口预测值，结果见表3。

2.2 二次指数平滑预测法

二次指数平滑法是对实际值进行2次加权平滑处理，结合平滑值建立预测模型的预测方法。该方法计算简单，需要的数据不多，可操作性强。此方法多用于时间序列数据的处理，而且对增长波动不大的数据较为有效。从前文的图1和图2来看，株洲市的人口数据基本满足这2点的要求，因此，利用1993—2012年株洲市常住人口的时间序列数据，来对未来人口进行短期预测是可行的。

2.2.1 二次指数平滑模型的公式及权数推导

二次指数平滑法模型公式为[6]

式中：T为从基期t到预测期的期数；

t+T为期预测值；

at, bt均为模型的参数，与平滑值相关。

为了求得模型的解，必须要先求出式（3）的第一、第二次平滑值St(1)和St(2)，其计算公式为

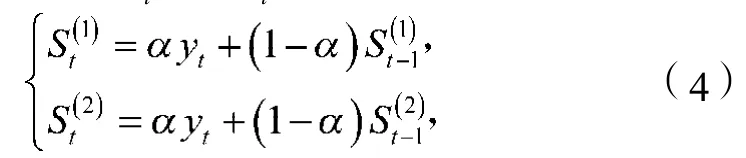
式中yt为t期的实际值。

表2 取不同值时的预测误差比较Table2The prediction error contrast for different values of

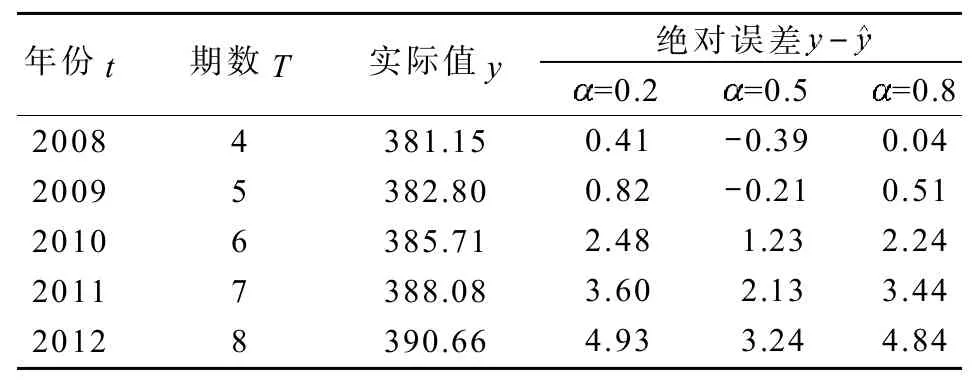
表2 取不同值时的预测误差比较Table2The prediction error contrast for different values of

年份t 2008 2009 2010 2011 2012期数T 绝对误差实际值y 381.15 382.80 385.71 388.08 390.66 4 5 6 7 8 =0.2 0.41 0.82 2.48 3.60 4.93 =0.5 -0.39 -0.21 1.23 2.13 3.24 =0.8 0.04 0.51 2.24 3.44 4.84

由表2可知，当=0.5时，二次指数平滑法的预测值与实际值的误差最小，因此，下面的预测就把=0.5作为加权系数的取值。

2.2.2 二次指数平滑模型的建立及预测结果

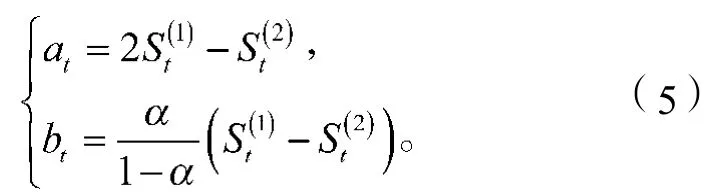
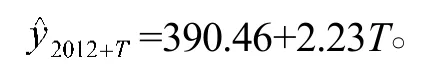
将2013年作为起始点，即T=1，就可以预测出2013—2020年的数据，预测结果见表3。

2.3 灰色GM（1, 1）模型预测法

GM（1, 1）模型预测法是灰色预测法中的一种主要方法，其预测对象主要是有时间序列的数列数据。由于该模型对于数据是否平稳的要求不高，且预测精度仅和样本容量相关，所以，运用该方法对样本充足、数据平稳度一般的株洲市常住人口的预测是可行的。

2.3.1 灰色GM（1, 1）模型的建立

灰色预测模型的建立具体步骤为：

1）数据的累加处理。在进行灰色预测分析之前，要先对数据进行累加处理，即将不平稳的原始数据平稳化。先设数列，x(0)(t)指t年的常住人口实际值，将1993年看做t的初始年份，则可得到，即原始数列。接下来套用累加公式[7]

将株洲市1993—2012年的常住人口实际值代入式（6），得到累加数列x(1)(t)，数列呈线性分布。

2）推导微分方程。由于累加数列x(1)(t)明显的呈现线性分布，所以可以利用微分方程对其进行描述。设微分方程为

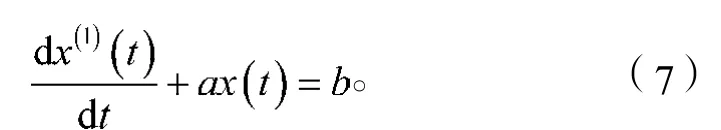
对于式（7）中的系数a和b可用如下的最小二乘法拟合得出：

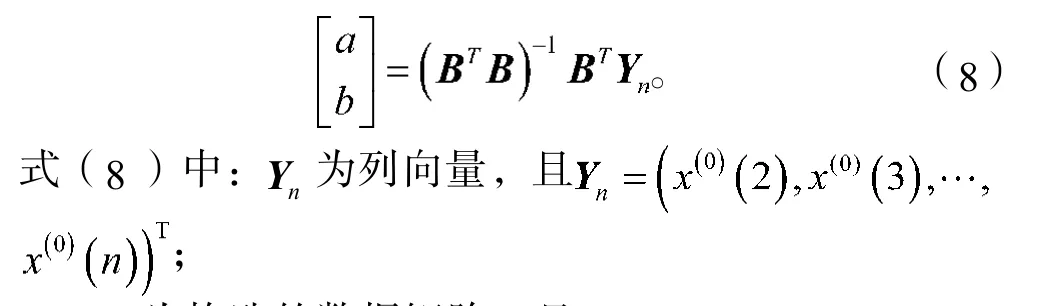
B为构造的数据矩阵，且

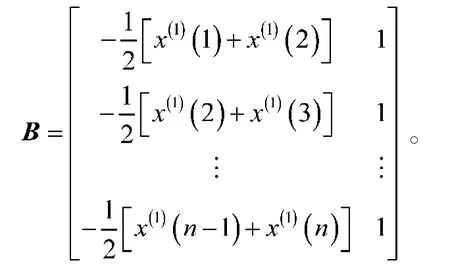
将式（6）求得的累加数列x(1)(t)的数据代入矩阵B，再将求出的矩阵B并代入式（8）运算可得

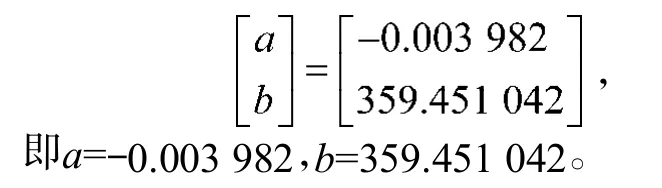
3）建立预测模型。微分方程（7）所对应的时间响应函数为

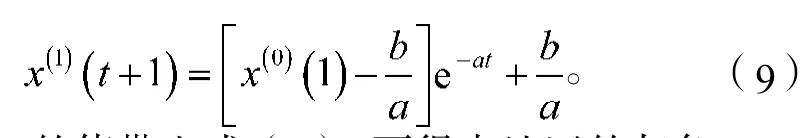
将a, b的值带入式（9），可得本地区的灰色GM（1, 1）预测模型公式为

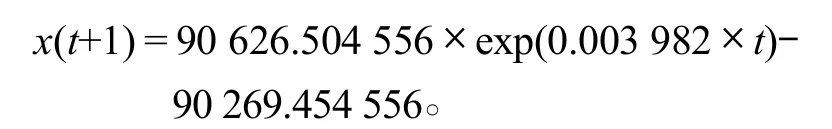
2.3.2 灰色GM（1, 1）模型的检验及预测结果

为了确定模型的预测精度和可靠程度，必须对模型进行检验。灰色GM(1, 1)模型的检验方法主要有2种：残差检验和后验差检验，它们分别用于检验模型的预测精度和预测结果的可靠程度。

1）残差检验

由于x(1)(t)的数据是累加数据，则可通过推导求出原始数据的还原值

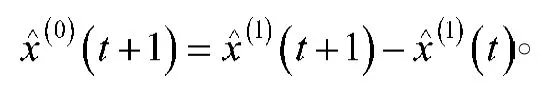
根据残差公式

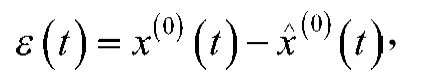
以及相对误差公式

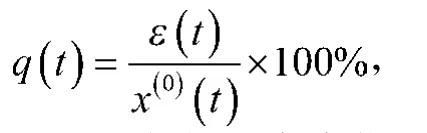
可以求得1993—2012年株洲市常住人口值的平均相对误差为0.00074%。可见模型精度较高，从而通过了残差检验。

2）后验差检验

在已知数据残差值和1933—2012年人口的实际值xt(0)的前提下，分别计算残差值的标准差S1和人口实际值的标准差，其值为：

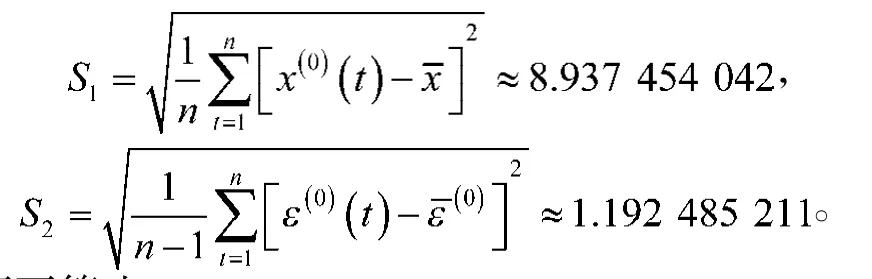
进而可算出

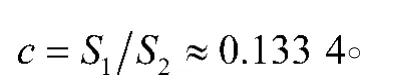
同时可算出小误差概率

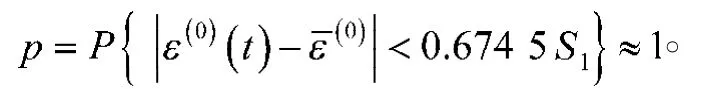
通过查等级标准表[8]可知，灰色GM（1, 1）预测模型公式的c, p两个值都在“好”的范围之内，模型预测精度和预测结果可靠程度都较高，可以用于对株洲市常住人口的预测。

将株洲市1993—2012年常住人口的实际数据代入灰色GM（1, 1）预测模型公式，可以得到2013—2020年的预测数据，详细预测结果见表3。

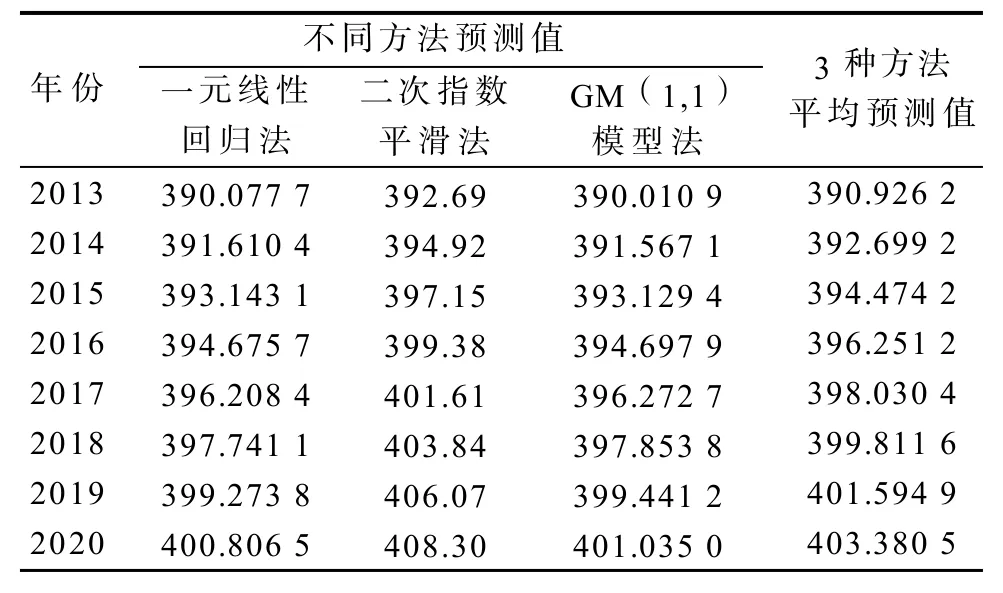
表32013 —2020年株洲市常住人口预测值Table3The predicted resident population of Zhuzhou City in 2013—2020万人

3 3种预测方法的比较分析

3.13 种预测方法的精度比较分析

对3种模型的检验和分析可知，3种方法的预测精度不同。选取2008—2012年株洲市的常住人口实际数据，与运用3种方法所求出的预测值进行比较，得出预测数据与实际数据的相对误差，见表4。

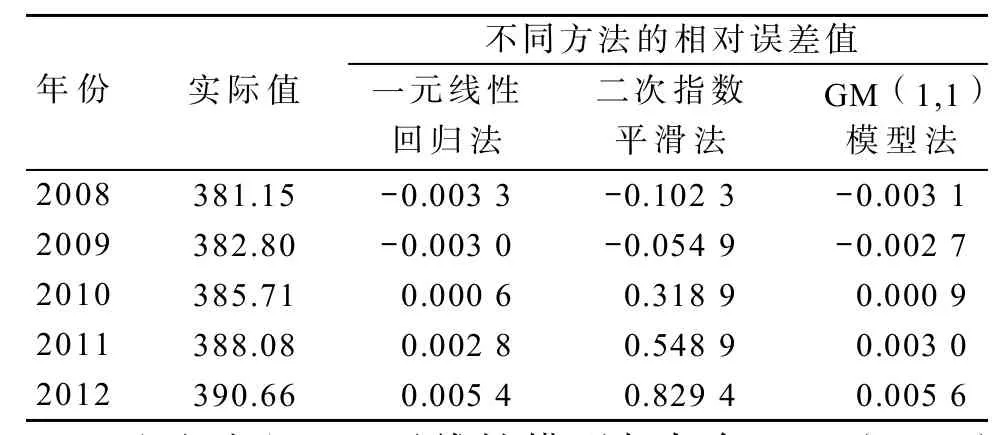
表42008 —2012年3种预测方法的精度对比Table4The prediction accuracy contrast of three forecast methods in 2008—2012

通过对比，一元线性模型与灰色GM（1, 1）模型的相对误差范围为-0.0033～0.0056，预测精度较高；二次指数平滑法模型的相对误差范围为-0.1023～0.8294，预测精度明显低于前2个模型。考虑到模型本身的适用性，灰色GM（1, 1）模型法，是基于添加了多种影响因素的前提下进行建模的，综合分析能力优秀。所以，灰色GM（1, 1）模型对株洲市常住人口的预测精度最高，一元线性回归法精度次之，二次指数平滑法精度最低。

3.23 种方法预测结果的综合分析

从一元线性回归法、二次指数平滑法以及灰色GM（1, 1）模型法的预测结果综合来看，3种方法预测的数据有一定差距，其中一元线性回归法和灰色GM（1, 1）模型法预测的结果相差较小，两者的平均绝对值差距量只有0.0898。而二次指数平滑法的结果与其他2种方法的结果差距较大，到预测结束的2020年，与其他2种方法的结果差距高达7.5。尽管3种预测方法的结果与精度各不相同，但综合考虑，将3种预测方法的结果相加求得的平均值作为本文最终的预测结果比较合适，结果见表3。

4 结论与建议

本文以1993—2012年株洲市的常住人口数据为基础，通过运用一元线性回归法、二次指数平滑法、灰色GM（1, 1）模型预测法，分别对2013—2020年株洲市的常住人口进行了短期预测，将3种方法预测结果的平均值作为最终的预测值。预测结果表明，到2020年株洲市的常住人口总量将达到403.3805万人。

《株洲城市总体规划（2006—2020）》中规定，到2020年常住人口控制在425万人以内。这表明预测数据较为合理，符合株洲市规划发展的预期目标，因此，本文所述的多模型预测的方法是可行的，对株洲市这种人口增长较稳定的地区的人口预测，具有较好的借鉴意义。

从预测结果可以看出，株洲市在本轮规划期（2020年）结束之前，常住人口还会增长10万人以上，地区常住人口很有可能达到或超过400万人的大关。这一结果将会对整个株洲地区产生多方面的影响。如基础设施建设和配套设施的规模要扩大，居住用地的面积将会进一步增长，“两型”建设的指标完成难度会增加等。对面这些问题与挑战株洲市应该早作准备，可以从以下几个方面着手：

1）在城市规划与管理方面，需要结合常住人口总量增加的趋势，合理调整原来的规划与设计，加快城市基础设施建设，搞好道路交通、水电气网络的扩展建设，有步骤地拓展城镇建设的区域，以适应株洲市常住人口增长的形势。同时，要发挥政府的积极作用，针对常住人口总量的增长，要推进“开源节流”措施。一方面，要做长远的规划，为将来的人口增长预留一定的空间，实现应对常住人口增长的“开源”；另一方面，要继续推进计划生育等人口政策，认真落实好户籍管理制度，严格控制人口的自然增长率以及人口机械增长量，达到常住人口“节流”的目的。

2）在经济发展方面，株洲市需顺应常住人口增长、人口流动速度加快的趋势，把握好人口红利门槛，结合国家的“中部崛起”战略，湖南省的“一带一部”定位以及株洲市自身的“打开湖南东大门”战略，同时，重点推进“动力谷”、“航空、轨道交通城”等其他高科技产业园区的建设与投资，把握发展机遇，实现株洲市的产业升级，打造株洲产业与经济发展的“升级版”，从而在2020年下一个规划期到来前，全面提升株洲市的整体经济水平。

3）在环境保护方面，一方面，可以充分利用好2007年以来“两型社会”和“国家园林城市”以及“国家卫生城市”的建设成果，完善已有的城镇环保和污染治理机制，夯实5年多的工作成果。另一方面，政府要加大宣传力度，动员更多市民群众加入到环保监督的行动中来，重点治理好湘江流域以及清水塘地区等污染较为严重的区域，在下一个规划期之前实现株洲市环境的大转变。

[1]黄荣清.关于人口预测问题的思考[J].人口研究，2004，28(1)：88-90. Huang Rongqing. Thinking About Population Prediction Problem[J]. Population Research，2004，28(1)：88-90.

[2]黄夏先.株洲“两型社会”建设中的人口均衡发展对策研究[J]. 经济研究导刊，2011(34)：161-163. Huang Xiaxian. Countermeasures to Population Balanced Development in Zhuzhou“Two-Oriented Society”Construction[J]. Economic Research Guide，2011(34)：161-163.

[3]胡科，石培基.区域研究中的常用人口预测模型[J].西北人口，2009，30(1)：94-98. Hu Ke，Shi Peiji. A Study on Prediction Models of Population in Region Study[J]. Northwest Population，2009，30(1)：94-98.

[4]张海峰，杨萍，李春花，等.基于多模型的西宁市人口规模预测[J].干旱区地理，2013，36(5)：955-962. Zhang Haifeng，Yang Ping，Li Chunhua, et al. Population Prediction of Xining City Based on Multi-Models[J]. Arid Land Geography，2013，36(5)：955-962.

[5]陈爱平，安和平.中国人口时间序列预测模型的探讨[J].人口与经济，2004(6)：63-67. Chen Aiping，An Heping. A Study on Chinese Population Forecast by Time Series Model[J]. Population & Economics，2004(6)：63-67.

[6]孟勤宪，黄涛.二次指数平滑法的成都市餐厨垃圾产量预测[J]. 四川环境，2010，29(4)：29-30. Meng Qinxian，Huang Tao. Quadratic Exponential Smoothing Forecast of Chengdu Food Waste Production[J]. Sichuan Environment，2010，29(4)：29-30.

[7]李凯.灰色预测模型及其应用[D]. 荆州：长江大学，2012. Li Kai. Gray Prediction Model and Its Application[D]. Jingzhou：Yangtze University，2012.

[8]徐建华.现代地理学中的数学方法[M]. 2版. 北京：高等教育出版社，2002：344-345. Xu Jianhua. Mathematical Methods in Contemporary Geography[M]. 2th ed. Beijing：Higher Education Press，2002：344-345.

（责任编辑：邓光辉）

Forecast Analysis of Area Resident Population Scale Under Multiple Model Method：Taking Zhuzhou City of Hunan Province as an Example

Song Hanjie
（School of Resources and Enviromental Science，Hunan Normal University，Changsha 410081，China）

With the permanent resident population of Zhuzhou City from 1993 to 2012 as sample data, analyzes the change of the resident population data in Zhuzhou City, and using the linear regression method, the quadratic exponential smoothing method and GM（1,1） model forecasting method, predicts Zhuzhou City's permanent population data of 2013—2020, and obtains the permanent population growth forecast data in Zhuzhou City in next 8 years. According to the prediction, puts forward the related proposals for dealing with the problems of the future resident population growth of Zhuzhou City.

Zhuzhou City resident population；population forecast；linear regression method；quadratic exponential smoothing method；GM（1,1） model method

C924.24

A

1673-9833(2014)06-0042-06

10.3969/j.issn.1673-9833.2014.06.009

2014-10-22

宋汉杰（1988-），男，湖南株洲人，湖南师范大学硕士生，主要研究方向为区域经济与区域发展，E-mail：910253056@qq.com