室内定位技术的多源数据融合算法研究
2014-05-04孙德辉
董 哲,吴 瑶,孙德辉
(北方工业大学 机电工程学院 现场总线及自动化重点实验室,北京100144)
0 引 言
随着物联网的广泛应用,移动定位技术成为了国内外热点研究课题之一。其中,由于GPS信号无法传播到室内、地下和隧道中,且易受到大树、山脉、城市内部高大建筑物的遮挡发生多路径效应,从而难以应用到室内[1]。在室内目标定位和跟踪等应用中,无线传感器网络正好可以弥补GPS定位性能的局限性,并且有效应用在智能家居、仓储管理以及安全防护等领域。因此对其技术的应用要求也越来越严格,主要体现于定位精度。
1 RSS和TOF定位技术研究
1.1 基于RSSI的距离测量
在信号传输过程中,移动节点接收到的信号强度会随着距离的变化而变化,利用理论和经验模型将传输损耗转化为节点间的距离。采用Log-normal Shadowing Model模型[2],公式如下

式中:d——固定节点到移动节点的距离,Pr(d)——固定节点接收到的信号强度,d0——参考距离,Pr(d0)——移动节点在距离d0时所接收到的信号强度。XdB——一个均值为0,方差为σdB的随机数,其中σdB为遮蔽方差,见表1。α为路径损耗指数,在不同的环境也会有很大的变化[3],见表1。

表1 不同环境下的路径损耗及遮蔽方差
由式 (1)可以看出,当α,σdB以及参考距离d0一定时,传播损耗10αlog(d/d0)和传播距离d呈线性关系,由于对数函数log(d/d0)在d的逐渐增大的变化过程中渐趋于平缓,传播损耗也随之趋于平缓。但是在实际情况下,随着距离d的增大,由于天线增益、反射、阻挡、多径传播等多种因素的影响,传播损耗和传播距离d之间的线性关系可能发生局部的剧烈变化,上述模型在这种情况下就会发生较大误差,定位精度会有所降低。即便如此,由于传感器节点本身具有无线通信的功能,相应硬件设备价格较低,且功率小,近年来仍被广泛应用于无线传感器网络基于距离的定位技术中。
1.2 基于TOF的距离测量
TOF测距技术也被称为飞行时差测距 (time of flight measurement)[4],主要靠两个射频设备之间传输数据包,根据数据包往返的时间差,来计算移动节点的距离。固定节点向移动节点发送一个数据包,当移动节点收到时立即向固定节点发送一个回复响应。
该模型公式如下

由dT=TTOF*C,其中C代表电磁波的速度,值为3*108m/s。可得

式中:dT——移动节点相对于固定节点的距离,TTOT——固定节点从发出数据包到接收确认的时间,TTAT——移动节点从收到数据包到回复确认的时间段,TRTT为数据包往返于两个节点间的飞行时间。φ(t)代表数据包在确认和应答过程中产生的干扰及延迟。
1.3 两种算法的对比
为准确了解两种测距算法的特性,本实验采集两组实测数据。通过使用无线射频模块CC2530在0~100米内采用RSSI和TOF算法分别进行测距分析。
由图1可知,采用RSSI算法测得的距离随着距离的增大,所受到的噪音等干扰也逐渐增大,与真实距离偏离也随之增大。在TOF算法测距中当距离近时,延迟时间有可能会大于飞行时间,即φ(t)>TRTT,在这种情况下测得的距离已经不可进行采用,作为死区。死区之外可看出随着距离增长,测得的距离呈现逐渐接近真实值的趋势。

图1 RSSI与TOF的测距对比
经过实验得知,在可视距传输LOS(line-of-sight)环境下,TOF测距方法能够弥补RSSI在距离估算上面的误差,但在近距离区域,TOF存在死区等干扰测量精确度会大大降低,而RSSI恰好能够弥补该区域的漏洞。
2 数据过滤
2.1 采集过滤
由上述式 (1)和式 (3)可看出,两种不同的测距方法均可得到移动节点到固定节点的距离,然而在采集数据的过程中,均会产生不同差值的噪音量,而多次测量的结果之间并没有必然联系。所以本文先采用R-EWMA算法,此算法由移动平均算法MA演变过来,它克服了移动平均算法高存储需求的缺陷,并通过对历史数据和加权指数进行线性结合,对距离测量值进行优化,是一种简单高效的评估算法[5]。k是一个字节窗口的最大值的可调节参数,即移动窗口。算法如下

前一时刻可表示为

其中,β=k/k+1,且0≤β<1。指数加权系数β就是对最近数据重视程度的权值,β越大,表示最近数据对于最终结果的影响越小,反之则越大。通过上式的计算可得到相应的
另外,异样噪声并不是唯一的不确定性测量问题。根据人的运动常规,事实上,在室内环境中,人的速度不会超过vmax=2m/s[6]。因此,可将超过此范围的变化量过滤掉

2.2 卡尔曼滤波
在无线通信中,设定两个无线节点在可视距环境下,根据运动学原理建立系统状态模型[7]

式中:s(t)——移动节点在t时刻的直线距离,v(t)——移动点在固定节点方向上的速度分量,也可称为径向速度,作为系统的输入,可通过v= [d(t)-d(t-1)]/Δt得到。d(t)作为系统的输出,输出移动节点到固定节点之间的距离。
将上述模型离散化,可表示为
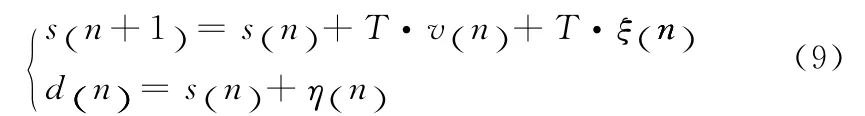
这里s(n)和v(n)分别表示移动节点接收到第n个数据包时的距离和径向速度,T为采样周期。ζ(n)和η(n)分别是系统的过程噪声和观测噪声,且满足ζ(n)∈(0,Qn),η(n)∈ (0,Rn),Qn,Rn是系统噪声ζ(n)和观测噪声η(n)的方差,取值取决于多种不确定条件的叠加,例如,天线的方位和存在的障碍物或墙壁。对于带有未知噪声分布的线性系统来说,卡尔曼滤波 (KF)是最优选的状态估计的方法。一般来说,对于典型的卡尔曼滤波算法,主要由预测阶段和更新阶段两部分组成。用上标*被来表示预测,根据文献[8]可由方程 (9)得到KF预测方程


3 融合算法
RSSI和TOF均可获取数据通过公式计算实现目标定位,不过在测距的过程中都夹杂着不小的噪音量,存在很大误差。其中一部分可通过卡尔曼滤波的方法滤掉,但还有一部分的噪音是无法测得也不容易去除掉的。由此,本文提出不同的融合算法来结合这两种测距算法以提高定位精度,并通过MATLAB仿真来观察融合效果。
3.1 平均法
经过同一运动轨迹的RSSI和TOF两种测距算法经过卡尔曼滤波后可得到和两条距离估计曲线。综合其两种测距方法,取其滤波曲线的平均值得到估计值。即

由图2可观察到,采用平均法融合后的曲线在大部分区域比单一算法更趋近于真实理想值,不过在死区及突变等区域受到的干扰较大,一概平均求值不够稳定且精度达不到理想值。

图2 平均法
3.2 加权法
此方法将两种不同测距技术性质特点作为融合因素引入实验,依照距离的变化分别对RSSI和TOF两种算法进行加权,使其均能发挥优势,避其短处,从而达到降低误差的效果。简单来说,可由下述方程来表示

其中可通过遍历算法获取ɑ的取值。
由图3可观察到,加权法很好的降低了:在距离近时TOF测距算法存在的死区等干扰对距离偏移的影响;以及距离远时RSSI测距算法存在的耗损和噪音产生误差的影响。但是对于临界值的选定,以及权值ɑ的取值都存在一定的不准确性,无法达到最优。由此本文提出神经网络法来解决此问题。
From the anisotropy coefficient of circular device γc =x1c/x2c and the oxidation depth of diamond device xd = (x1c +x2c)/2, we got:

图3 加权法
3.3 神经网络法
神经网络是由多个简单的处理单元 (也称为神经元)广泛地互相连接而形成的一个复杂网络系统,可以进行大规模的并行、分布式存储和处理、自组织、自适应和自学习。
3.3.1 建立神经网络
鉴于网络连接的拓扑结构和神经元的特性,本文构建前馈型BP网络进行训练,BP网络的算法[9,10]核心是误差反向传播来修正各个节点的权值和阈值。
图4即为所构建的网络结构,其中输入层有两个神经元xi,分别为RSSI和TOF经过卡尔曼滤波的距离值,隐含层选取3个节点yj,输出层有一个节点zk,输出真实状态T。输入层与隐含层之间的权值为wji,隐含层与输出层之间的阈值为wkj,阈值函数为θ。输入信号通过隐含层运算传给输出层,与输出层的预期结果进行比较,计算出误差,并将误差反向传播,从而不断更新权重缩小误差。
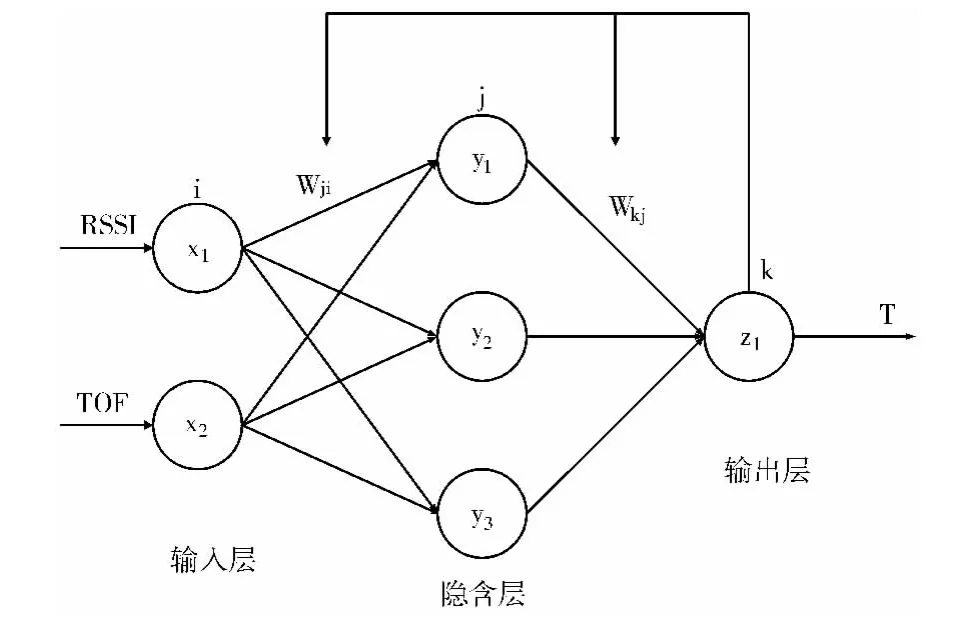
图4 BP神经网络结构
3.3.2 训练神经网络
用newff()函数创建一个前向型BP神经网络,然后直接调用train函数进行训练,传递函数为tansig(),设定训练目标误差为3e-3,最大训练次数为1000,采用标准的梯度下降算法进行训练。

图5 神经网络训练
3.3.3 神经网络仿真
由于newff()函数是具有随机性的,所以每一次的训练结果会有所不同,当训练达到期望值后可使用sim函数进行仿真。
由图6可以看出较于加权法,神经网络法与真实值的拟合程度更高,收敛的更快,且稳定性强。

图6 神经网络法
3.4 算法对比
为了更好的观察所提出各算法的优劣,本文将其进行对比分析。如图7所示。
由图7可以看到,RSSI在远距离时与真实值偏离较大,TOF在近距离时存在死区等问题影响定位精度。平均法在误差跳动大的区域也存在较大偏离。而加权法虽然明显地使噪音的波动幅度得到了收敛,但是精度较低,不够理想。通过神经网络训练后的距离估计值,与真实值的拟合程度最高,精度较大幅度提升。其中,为了可以更直观地对比误差大小,实验分别比较了测距算法所得到的估计值与真实值之间的欧式距离[11]。
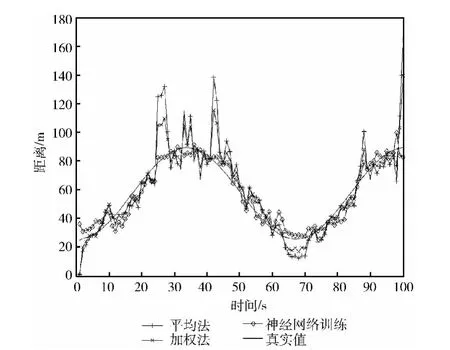
图7 融合算法对比
在表2中,通过对所列几种算法进行误差比较可以看出,神经网络算法的误差值最小。

表2 误差值对比
4 结束语
本文主要研究了一种融合RSSI和TOF的数据混合算法。首先分别对RSSI和TOF两种方法进行了详细的分析,并通过R-EWMA算法减少输入宽带噪声,消除了随机出现的突变量噪声,然后将RSSI和TOF的算法利用卡尔曼滤波进行算法融合,得到多个能够降低误差的方法,将其进行模拟仿真,经过对比分析,结果表明通过神经网络算法融合后的距离测量最为精准。
[1]WANG Xiaohui,WANG Yunjia,ZHANG Wei.Review of indoor positioning technology based on RFID [J].Transducer and Microsystem Technologies,2009,28 (2):1-3 (in Chinese).[王小辉,汪云甲,张伟.基于RFID的室内定位技术评述 [J].传感器与微系统,2009,28 (2):1-3.]
[2]ZHU Jian,ZHAO Hai,XU Jiuqiang,et al.Localization model in wireless sensor networks [J].Journal of Software,2011,22 (7):1612-1625 (in Chinese).[朱剑,赵海,徐久强,等.无线传感器网络中的定位模型 [J].软件学报,2011,22 (7):1612-1625.]
[3]Xu J,Liu W,Lang F,et al.Distance measurement model based on RSSI in WSN [J].Wireless Sensor Network,2010,2 (8):606-611.
[4]CHANG Huawei,WANG Fubao,YAN Guoqiang,et al.TOF ranging method for w ireless sensor networks [J].Modern Electronics Technique,2011,34 (1):35-38 (in Chinese).[常华伟,王福豹,严国强,等.无线传感器网络的TOF测距方法研究 [J].现代电子技术,2011,34 (1):35-38.]
[5]BI Weiwei.Research and implementation of anti-interference location algorithm based on RSSI [D].Shenyang:Northeastern University,2009 (in Chinese). [毕伟伟.基于 RSSI的WSN抗干扰定位算法研究与实现 [D].沈阳:东北大学,2009.]
[6]Karamouzas I,Overmars M.A velocity-based approach for simulating human collision avoidance [C]//Intelligent Virtual Agents.Springer Berlin Heidelberg,2010:180-186.
[7]Macii D,Trenti F,Pivato P.A robust wireless proximity detection technique based on RSS and ToF measurements [C]//IEEE International Workshop on Measurements and Networking Proceedings,2011:31-36.
[8]Grewal M S,Andrews A P.Kalman filtering:Theory and practice using MATLAB [M].Wiley,2011.
[9]Wu W,Wang J,Cheng M,et al.Convergence analysis of online gradient method for BP neural networks [J].Neural Networks,2011,24 (1):91-98.
[10]SHI Xiaowei,ZHANG Huiqing,DENG Guihua.Research on indoor location algorithm based on distance-loss model using back propagation neural network [J].Computer Measurement and Control,2012,20 (7):1944-1947 (in Chinese).[石晓伟,张会清,邓贵华.基于BP神经网络的距离损耗模型室内定位算法研究 [J].计算机测量与控制,2012,20(7):1944-1947.]
[11]JIA Zixi.A research on the localization and tracking method in wireless sensor network [D].Shenyang:Northeastern University,2009(in Chinese).[贾子熙.无线传感器网络定位与跟踪方法研究 [D].沈阳:东北大学,2009.]
