浅谈基于矩阵运算的碎纸片拼接问题

刘　令，刘　元，孟凡清

（1.吉林建筑大学，长春　130118；2.长春一汽实业建筑装饰工程有限责任公司，长春　130011）

浅谈基于矩阵运算的碎纸片拼接问题

刘令1，刘元2，孟凡清1

（1.吉林建筑大学，长春130118；2.长春一汽实业建筑装饰工程有限责任公司，长春130011）

摘要：随着科学技术的不断发展，碎片拼接技术在军事、医学、文物鉴定等各生活领域得到广泛的应用。碎片拼接复原其核心思想就是先将图像数字化，然后从图像边缘等概率提取子矩阵，根据计算机相应的程序对其进行拼接处理，最终实现全自动或是半自动的拼接复原。

关键词：矩阵分析法；角点检测算法；匹配测度模型

1　碎纸片纵切模型

是对于给定来自同一页印刷文字文件的碎纸机破碎纸片（仅纵切）进行拼接复原，我们采用MATLAB中imread函数将附件1中的19条图像信息转化为1980*72的像素矩阵，由于纵向文本信息过大，将其取逆矩阵，根据阈值分割方法［1]，我们给定阈值为127，即0～127像素值用0代替，128～255像素值用1代替。把8位灰度图像运用阈值方法转换为二值0—1图像。再将矩阵按列向量分割为52个子矩阵，再由聚类分析法取出两个子矩阵，用C语言编程将其最右侧列向量与其它图像信息对应子矩阵进行匹配，找到相似性最大的文本信息。以此类推，可将条状碎片拼接成完整的图像信息，比较时则需要人工干预。最后根据得到的一维数组的序号运用MATLAB把这些序号的图像拼接起来将纸条复原。

1.1灰度图像的读取

8位灰度：28=256种像素点，（黑到白）每像素对应一个值，取值为0～255，每值对应一灰度，读取完数据后8位灰度图像变成一个二维矩阵。

读取8位灰度图像：函数imread可以从MATLAB支持的图像文件格式.bmp中读取图像。格式为：I=imread（‘FILE’），其中，FILE为需要读入的图像文件名称。

I=imread（'C：UsersahuoDesktopB附件100.bmp'）；

1.2I'%矩阵的转置

把19个纸片的533～570和1483～1520两个子矩阵选取到两个二维数组中，运用C言的循环编程方法［2]得到了碎纸片的排列顺序，最后用MATLAB进行图像复原。

2　碎纸片横纵切模型

采用角点检测算法中的Harris角点检测算法，记录各角点的坐标向量从而更加准确的描述八位灰度图像的像素点位置。通过二元偏微分方程找出碎纸片纵向边沿到文字最上或最下端的距离，求其每两个纸条的距离进行期望运算匹配，将其连接成纵向纸条，若出现多个相似边缘距离，这就需要人工干预，将其上下连接。再用问题一的解决方法，将其碎纸片拼接复原。

该算法的基本原理是取以目标像素点为中心的一个小窗口，计算窗口沿任何方向移动后的灰度变化，并用解析函数形式表达。设以像素点（x，y）为中心的小窗口在X方向上移动u，y方向上移动v，Harris给出灰度变化度量的解析表达式［3]：

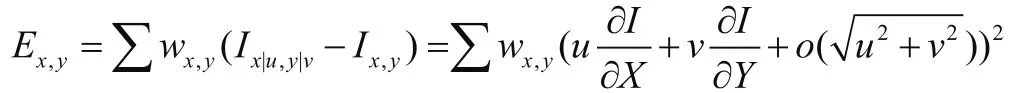
M为实对称矩阵，将其对角化处理最终得到：其中，R为旋转因子，对角化处理后并不改变以u，v为坐标参数空间曲面的形状，其特征值反应了两个主轴方向的图像表面曲率。当两个特征值均较小时，表明目标点附近区域为“平坦区域”；特征值一大一小时，表明特征点位于“边缘”上；只有当两个特征值均比较大时，沿任何方向的移动均将导致灰度的剧烈变化。

纸条进行Harris角点检测后，分别得到角点对应与该图像的坐标位置，以该坐标位置为中心，分别取其附近的8个像素值，然后进行与另一纸条进行匹配，找出距离最小的点作为匹配点。将纸条中的角点与另一纸条的所有角点进行相减，得到一个最小误差值，并记录下该位置，这样依次将纸条一中的角点都进行相减，即可得到最佳匹配的纸条。

3　正反面碎纸片横纵切模型

首先仍通过MATLAB程序编程将碎纸片转化为八位灰度图像，通过阈值分析并取子矩阵转为二元向量。分别抽取每个碎纸片所有行和列向量，运用向量相似度测量方法中的相似系数（SMC），比较每个纸片四个边上的匹配系数，找到与之相似系数最大的碎纸片，即为可能相邻纸片，最后通过MATLAB程序将图片复原。由于存在正反两面，可能出现多个相似度较大的碎纸片，此时需要人工干涉。

首先，读取图片到MATLAB中，并显示为矩阵，然后，运用第一问的阈值分析法转换为二元矩阵，对左侧图像上边、左边、下边、右边分别取出子矩阵，运用MATLAB编程将图片的子矩阵分别与下一张图片的对应子矩阵进行相似函数匹配，再进行相似系数运算当相似系数越接近1时，这两张纸片越可能复原，必要时加入人工干预。运用二元向量的相似函数［4]求解，相似性函数是用函数的方法表征两向量的相似程度，只有两个状态（0或1）的变量称为二元变量，由二元变量组成的向叫做二元向量。设x和y为二元向量，x=（x1，x2，x3…，xn）`，y=（y1，y2，y3…，yn）`，则这两个向量的匹配数目定义为：

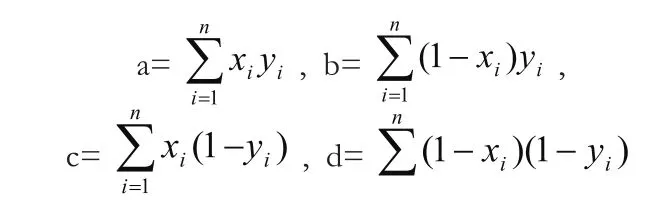
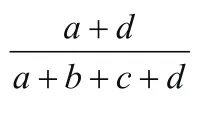
Sim（x，y）=当该系数越大两个向量越匹配。

模型的推广

以上碎片拼接模型模型是针对横切和纵切两种切法，现实生活中很难达到全是横纵切理想状态，因此，可以进一步扩展为其它形式的切法，例如倾斜切法，依然可以应用上述类似原理进行图片的拼接和复原，不过由于边界线是倾斜的，此时可考虑直线方程的拟合，这时线性模型y=ax+b也就建立起来了。再比如当碎纸片的轮廓线是不规则的，可考虑首先拟合成曲线方程y=a+bx+cx2+dX3+…….，通过曲线方程相似度的比较进行碎纸片的轮廓匹配。

参考文献：

［1]尚涛，谢龙汉，杜如虚.MATLAB工程计算及分析［M].北京：清华大学出版社.2011-03.

［2]谭浩强，C程序设计（第三版）［M].清华大学出版社.北京：2012.

［3]张宇，刘雨东，计钊.向量相似度测量方法［J].声学技术.第二十八卷第四期：533-536，2009.

［4]sunpea05，图像中角点（特征点）提取与匹配算法［Z]，http：//download.csdn.net/download/sunpea05/4291216，2012-05-12.

［5]张志涌.精通MATLAB［M].北京：北京航空航天大学出版社.2011.