基于工件形状特殊且存在大倒角及大过渡圆弧的加工
2014-05-03赵志彪天津市天重江天重工有限公司天津300402
赵志彪(天津市天重江天重工有限公司,天津300402)
基于工件形状特殊且存在大倒角及大过渡圆弧的加工
赵志彪(天津市天重江天重工有限公司,天津300402)
阐述了形状不规则的(不能在车床加工的工件)且存在大倒角孔或过渡圆弧的工件在SIEMENS840D数控落地镗铣床上的加工,利用SIEMENS840D系统中的R参数的功能,编写大倒角和大过渡圆弧加工程序时的加工思路、刀具的选择、数控程序的编制以及应注意的问题,该程序的加工使用既可以获得正确的R 圆弧轮廓形状和尺寸,又能极大的提高加工生产效率。
大倒角;倒圆弧;R参数;数学建模;加工程序
我公司是大型铸锻件生产及加工的企业,经常有压机的重要部件在我公司加工,而工件的设计中,往往存在大倒角及大过渡圆弧,而且所需要加工的大倒角及大过渡圆弧有较高的粗糙度要求Ra≤1.6。如果采用普通机床、传统刀具的加工方法,加工难度系数大,很难保证正确的尺寸、轮廓及粗糙度的要求,且生产效率低;采用数控编程的加工方法,可以实现准确的轮廓,加工后抛光打磨即可达到图纸要求的理想倒角或过渡圆弧。
我公司有一台齐二机床厂的TK6926数控落地镗铣,设备主要参数如下:
数控系统:SIEMENS840D数控系统
主轴直径:260mm
滑枕(W)行程:1500mm
主轴(Z)行程:1500mm
横向(X)轴行程:14000mm
纵向(Y)轴行程:6000mm
1 大倒角的加工方案研究
1.1 加工刀具的选择
我公司生产的上横梁,存在如“图一”所示的大倒角。
加工此倒角,理论上应该用可转位盘形铣刀,刀片是圆弧形状的,在切削过程中圆弧面与直面之间的切削,切削时接触面积大,可少次进刀即可达到理想的加工效果;刀具直径315mm,刀具圆弧为R8。
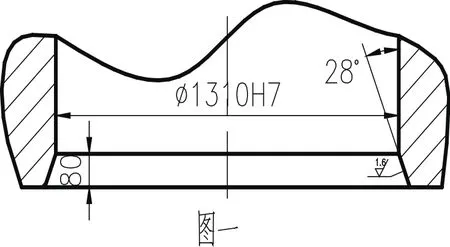
在我分厂现在没有可转位盘形铣刀故,在加工前可用普通合金切刀,刀具磨成如图二所示半圆弧形状,夹在刀盘上,实测刀体半径和刀具圆角半径,同样可以达到理想效果,只是加工效率偏低,现在以图二的刀具为准,确定工件加工方案。
该倒角的加工利用数控机床的三轴联动功能,编程的零点以及刀具的零点设置的是否合理直接影响着刀具在加工过程中的进刀、退刀的方便性。因此,孔端面为编程的XY 平面,X、Y零点为孔的中心位置,Z轴为加工深度为进给方向;在Z 轴方向对刀时,刀盘的刀片接触到孔端面设为Z轴坐标零点。
1.2 R参数的定义及数学建模
“图二”所示为编程零点及工件切入和切出位置。
1.2.1 R参数的设定及解释

R1 倒角的角度
R2 倒角的深度
R3 孔半径
R4 刀盘半径-刀片圆角半径
R5 刀片圆角半径
R6 X 轴方向上,刀具中心到编程零点的距离R7 Z 轴方向上,刀具中心到编程零点的距离R8 每次X向的进刀量
1.2.2 数学建模
本程序的编写方法是通过分析刀具在加工过程中的刀具中心的运动轨迹,计算分析找到“图三”中刀具中心点( A 点)的运动轨迹的规律,来加以编程;A 点为刀具中心点,是相对编程零点在X 和Z 轴上的坐标为( R6,R7)位置点。
其坐标为( R6,R7)位置点的数学模型如下:R6= R3+R2*TAN(R1)-R5*COS(R1)-R4-R8

R7=-R5+R5*SIN(R1)-R8/TAN(R1)
1.3 加工程序及部分程序解释
R1=28(倒角角度)
R2=80
R3=655(孔半径)
R4=137.5(除去刀具圆角的刀体半径)
R5=8(刀具半径)
R8=0(Z方向上每次进刀深度)
R6= R3+R2*TAN(R1)-R5*COS(R1)-R4-R8TAN(R1)
R7=-R5+R5*SIN(R1)-R8
N05 M31 M33 M35
N10 G00 G90 G54
N15 G00 X0 Y0 Z50
N20 M42 M3 S400 F2000
N25 G01 X=-R6 Y0 Z=R7(刀具走到倒角起始加工位置)
N30 G02 X=-R6 I=R6(沿着孔壁旋转一周加工)
N35 R8=R8+1(给R8赋值,每次加工完一整圈后Z轴方向上进给1mm)
N40 IF(R8<=80)GOTO N25(如果进给深度小于等于80mm时,程序跳转到N25程序段,继续执行循环程序,共执行81次)
N45 G00 X0 YO(加工完成返回编程零点)
N 50 Z50
N 55 M 30(程序结束)
2 大过渡圆弧的加工方案研究
大过渡圆角如“图四”所示,加工刀具仍为直径315mm,刀具圆弧为R8;编程零点如“图二”所示;工件切入和切出位置为圆弧与直线的切点。
2.1 数学建模
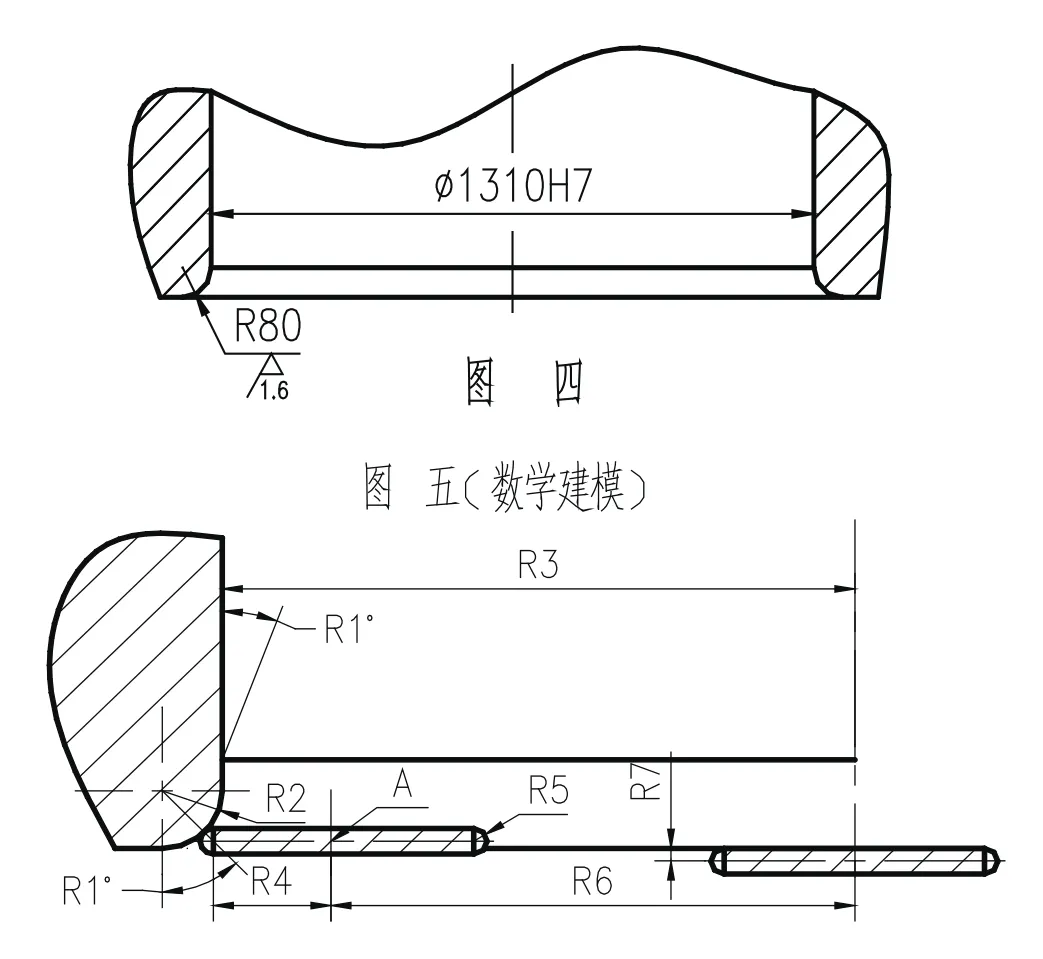
计算分析找到“图五”中刀具中心点( A 点)的运动轨迹的规律,来加以编程;A 点为刀具中心点,是相对编程零点在X 和Z 轴上的坐标为( R6,R7)位置点。
其坐标为( R6,R7)位置点的数学模型如下:
R6= R3+ R2-(R2+ R5)* SIN( R1)- R4
R7=(R5+R2)*COS(R1)-R2
2.2 加工程序及部分程序解释
R1=0(每次以角度的形式进刀)
R2=80(倒角半径)
R3=655(孔半径)
R4=137.5(除去刀具圆角的刀体半径)
R5=8(刀具半径)
R6=R3+ R2-(R2+ R5)* SIN( R1)- R4
R7=(R5+R2)*COS(R1)-R2
N05 M31 M33 M35
N10 G00 G90 G54
N15 G00 X0 Y0 Z50
N20 M42 M3 S400 F2000
N25 G01X=-R6 Y0 Z=R7(刀具走到倒角起始加工位置)
N30 G02X=-R6 I=R6(沿着孔壁旋转一周加工)
N35 R1=R1+1(给R1赋值,每次加工完一整圈后角度增加1°,控制进给)
N40 IF(R1<=90) GOTO N25(如果进给角度小于等于90°时,程序跳转到N25程序段,继续执行循环程序,共执行91次)
N45 G00 X0 YO(加工完成返回编程零点)
N50 Z50
N55 M30(程序结束)
3 总结
以上所介绍的大倒角及大过渡圆弧的加工思路以及数控加工的编写,使我分厂先进的数控机床得到了很好的应用,充分体现先进的数控机床和合理的数控刀具选择,所带来生产上的高效率,由于在实际加工过程中,没有理论刀具,可以根据实际加工需要,自制合理的刀具,同样可以达到理想的加工效果。
[1]梁炳文.机械加工工艺与诀窍精选[M]北京:机械工业出版社,2005.
[2]Sinumerik 840D基础编程手册[K].
[3]《机械加工工艺手册》[K].机械工业出版社;第1版(2003年1月1日).
赵志彪(1985—),男,本科,工程师,研究方向:数控机床大圆角及倒角的加工。
