FANUC系统椭圆程序编制中参数方程的应用
2014-04-29曹志文
曹志文
摘 要: 在数控加工中编制椭圆程序时,采用参数方程计算角度值、坐标值,按照参数方程五个步骤编制椭圆程序,方便、简单、易理解。
关键词: 椭圆 参数方程 坐标 变量 象限
在数控车削加工中,会遇到工件轮廓是椭圆方程曲线的情况,此时可采用宏程序完成椭圆方程曲线的加工。椭圆轮廓的程序可通过椭圆的一般标准方程和参数方程设计加工走刀路线,因为椭圆的参数方程比较方便。
椭圆的标准方程为:X2/a2+Y2/b2=1,参数方程:X=asinθ,Y=bcosθ,转换成工件坐标系中的参数方程:X=bsinθ,Z=acosθ,此方程中,不论a、b是长半轴还是短半轴,b指X方向的半轴,a指Z方向的半轴。参数方程椭圆程序编制简单分成五个步骤:
1.参数定义。用公共变量#100~#199、#500~#999中任一参数可定义方程中各变量,在这里我们用变量#101、#102、#103来编程,#101作为角度变量,#102作为X轴变量,#103作为Z轴变量。
2.计算点坐标。参数方程中初始角度的计算,根据公式X=bsinθ,Z=acosθ,a、b值已知,X、Z已知其中一个参数值,可得θ值和另一参数值。一般已知工件零点设在工件端面与中心线相交处。由于椭圆方程原点不在工件零点处,椭圆轮廓向X轴正方向平移了距离c,因此,在计算X坐标时,加上2倍的c距离,椭圆轮廓向Z轴负方向平移了距离d,因此,在计算Z坐标时,必须减去距离d。
3.插补。坐标插补用G01完成。
4.角度的递增或递减。参数#101角度的变化,以计算每个角度值对应的椭圆上X、Z的坐标值。
5.条件转移(IF语句)。程序变量增加一个增量,插补一个点,当插补过程还没有完成时,要重复以上过程,所以要使用循环判断判断是否到达终点,“否”继续循环,“是”结束循环,向下执行。这里,我们可以运用#101、#103来判断,角度和Z方向的值都是单调递增或递减,当椭圆没有过象限,#102单调递增或递减时,也可以用来循环判断,通常用#103判断比较方便。
椭圆轮廓程序格式如下:
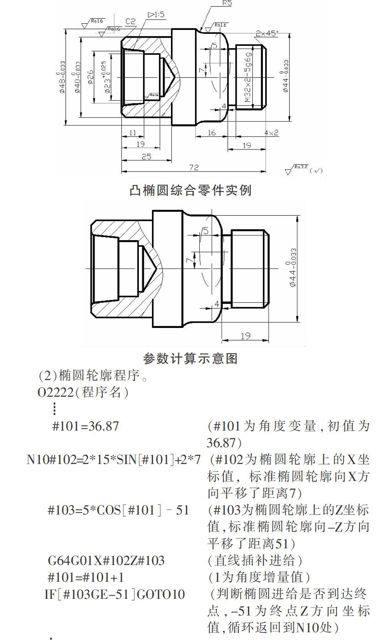
下面的零件图,椭圆轮廓的程序编制如下:
(1)相关计算。椭圆Z方向的半轴为5,X方向的半轴通过间接计算为44/2-7=15,椭圆起始点的Z值为4,代入椭圆参数方程Z=acosθ,可得θ=36.87。椭圆轮廓向Z轴负方向平移了19+4=23mm,椭圆轮廓向X偏移了7mm,椭圆轮廓终点Z方向的坐标值为-23。
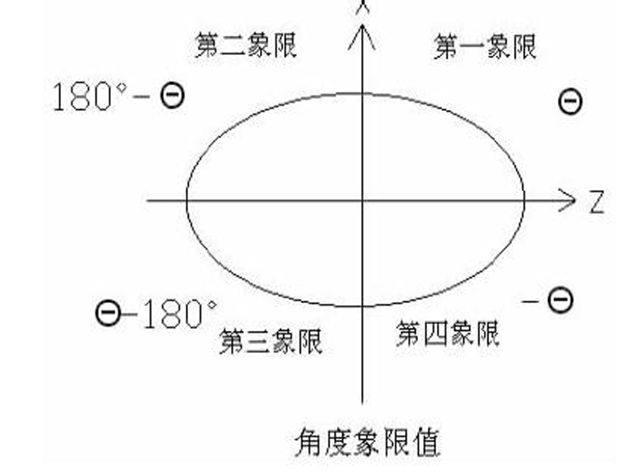
当椭圆轮廓是凹椭圆时,格式与以上基本相同,第1步和第4步稍稍发生了变化,用参数方程计算出的θ值,范围是0≤θ≤90,具体的取值从图形上部(即后置刀架)看,椭圆轮廓上该点在第几象限,第一象限为θ值,第二象限为180-θ,第三象限为θ-180,第,四象限为-θ。第4步变化是角度增量值变为角度递减值。
下面零件图中的凹椭圆轮廓程序编制如下:
(1)相关计算。X方向的半轴为12,椭圆Z方向的半轴为18,
椭圆起始点的X值通过间接计算为32/2+12-40/2=8,代入椭圆参数方程X=asinθ,可得θ=41.81,由于起点在第四象限,所以角度为-θ,即为-41.81,椭圆轮廓向Z方向平移了44mm,椭圆轮廓向X方向偏移了32/2+12=28mm,椭圆轮廓终点Z方向的值没有直接给出,X值与起始点值相同,θ为41.81,可以用角度循环判断,由于终点在第三象限,因此角度为θ-180=41.81-180=-138.19。
当遇到零件中有椭圆轮廓时,使用以上编程步骤即可,把椭圆编程的内容放在G73固定循环里,就可以完成粗精加工。