浅谈现代数学在小学数学中的渗透
2014-04-29黄玲侠
黄玲侠
【摘要】 现代数学与小学数学教育有着千丝万缕的关系. 本文从三个方面论述了在小学数学中渗透相关现代数学知识的方式及意义:一、渗透现代数学知识,丰富学生知识面;二、利用现代数学知识,解决小学数学中的一些疑难问题;三、巧用现代数学知识,体现数学的教育价值.
【关键词】 现代数学;小学数学;渗透
数学史上现代数学时期一般是指由19世纪20年代至今,这一时期产生的数学科学的分支主要包括:集合论、非欧几何、抽象代数、拓扑学、模糊数学等.
小学数学虽然简单,但它与现代数学基本上是特殊与一般的关系,因此小学数学中很多方面与现代数学有着密不可分的关系. 现代数学中蕴含了很多有趣的现象,比如绚烂多姿的分形图形、奇妙的莫比乌斯圈、荒诞而真实的非欧几何等. 在小学数学中适当渗透一些现代数学知识将会使小学数学课堂变得丰富多彩,有助于小学生数学情感价值观教育、数学美学教育,从而提高學生的数学素养.
(一)渗透现代数学知识,丰富学生知识面
在小学进行相应知识教学时,适当地介绍一些现代数学知识,有利于进一步拓展学生的视野,提升学生的素养.
比如,在小学,当“三角形内角和”单元教学完后,作为课堂延伸,或者第二课堂的内容,可以适当地介绍一下“罗氏几何”(罗巴切夫斯基几何),使学生了解三角形内角和为180度,是在欧几里得几何中成立的一个结论,而在“罗氏几何” 中三角形内角和是小于180度的;相应的,在“黎曼几何” 中,三角形内角和是大于180度的. 当然,这种知识,只能是给学生简单地介绍一下,让学生作为了解,使学生明白,数学的一些相应结论应对应于一定的体系,同时使学生体会到数学的神奇.
另外,《新课标》中要求学生“获得一定的数学思想方法”. 在给小学生进行“对应”思想的教学时,可以介绍“希尔伯特旅馆”的故事. 在这个故事里,一个有无穷个房间的旅馆住了无穷个客人,结果再来1个客人、再来100个客人、再来无数个客人,老板都可以用“一一对应的方法”让他们全部住下. 这种“一一对应”的方法,在小学中经常用到,而“希尔伯特旅馆”中,其实牵扯到了现代数学中无限集合中的可数集合的相关知识. 通过这个故事的介绍,一方面,可以加深学生对对应思想的理解,同时,可以使学生体会到数学的奇妙与有趣.
(二)利用现代数学知识,解决小学数学中的一些疑难问题
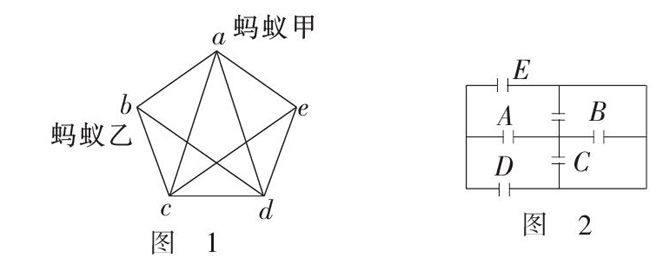
应用现代数学的相关知识有时可以使小学数学中的一些疑难问题得以轻松解决. 如图1所示,甲、乙两只蚂蚁分别处在图中顶点a,b处. 蚂蚁甲对蚂蚁乙说:“咱们俩比赛,看谁先把这个图的9 条边都爬过一遍后到达顶点e?”蚂蚁乙欣然同意. 假设两只蚂蚁的速度是一样的. 请问:最后的结果是怎样的呢?
再如,图2是某展览馆的平面图,一个参观者能否不重复地穿过每一扇门?如果不能,请说明理由;如果能,应从哪开始走?
像这样的小学数学问题,都可以转化为现代数学拓扑论中的一笔画问题,利用一个图形能一笔画的充要条件,从而使问题得到解决. 而图形能一笔画的充要条件——图形中奇点个数为0或2,小学生也完全可以理解,因为它只需要判断每个点发出的线段条数的奇偶性即可.
(三)巧用现代数学知识,体现数学的教育价值
义务教育新课标中,培养目标的三个维度之一即为“情感态度价值观”,借助于现代数学知识,可以对学生进行这方面的教育.
一方面,现代数学,在生活中无处不在,借此可以让学生体验到生活中处处有数学,以增强学生学习的兴趣.
如大自然中的分形现象:一棵大树是由树干和树干上的一些分叉长出来的树枝组成,如果把它的一个树枝锯下来后又会发现,该树枝是由树干和它的一些分叉长出来的更小的枝条组成,其构成形式与原来的大树相似. 像这种部分与整体具有的自相似性,就是现代数学中的分形现象. 生活中,树叶、弯弯曲曲的海岸线、起伏不平的地形外貌、人体组织的结构等,都具有分形的特点. 此外,在日常生活中随处都能碰到的条形码也是现代数学编码技术为我们带来便利的杰作. 这些都是小学生很熟悉的生活中的例子, 也比较容易为高年级的小学生所接受, 通过这些例子不难让学生感受到数学在生活中的威力.
另一方面,结合现代数学,可以对小学生开展美育教育. 例如, 通过荷兰著名艺术家埃舍尔的彩色木板画《圆的极限》 《魔鬼与天使》,让学生感悟艺术与现代数学中非欧几何相结合的曼妙奇异;通过瑞典科学家科赫用极其初等的办法构造的“科赫雪花”与自然界雪花的对比,可以满足小学生的审美特征, 还能唤起他们对数学的好奇,而这个例子只用到“等边三角形”这个概念, 只要教师在教学中应用合适的语言适时渗透, 小学生是能够理解的.
总之,在小学数学教学过程中,适当地渗透现代数学知识,有利于小学生数学素养的提升以及数学兴趣的培养.
【参考文献】
[1]课程教材研究所,数学课程教材研究开发中心.现代数学概论[M].北京:人民教育出版社,2003.
[2]易南轩,王芝平.多元视角下的数学文化[M].北京:科学出版社,2007.
