遗传算法在排课系统中的优化研究

叶碧虾

(漳州职业技术学院计算机工程系，福建 漳州 363000)

课程表针对高校教学计划进行了时间安排，是学校教学工作的指挥调度表，对学校其他工作的安排也有直接影响.对课表编排问题的数学模型、解的存在性以及计算机求解算法等问题国外研究人员是从20世纪50年代就开始进行了研究，但由于实际教学活动中各种复杂的约束条件而使相关算法无能为力［1］.对排课问题的研究国内始于上世纪90年代初期，当时的系统都是模拟手工排课过程，以“班”为单位，采用启发式函数来进行编排的，但是这些课表编排系统比较依赖于各个学校的教学体制，不宜于广泛推广［2］.

目前，国内解决排课问题的主要方案大体可分为:(1)基于传统数学和运筹学方法，但随着问题规模的扩大，这类方法就越难求解;(2)人—机交互方法，但这种半自动化的方式还是太过于耗时和耗工作量;(3)人工智能方法和基于启发式算法的方法，人工智能在各领域的应用已经很广泛，在解决排课问题中主要采用约束满足和专家系统，而启发式算法主要是采用模拟退火算法、遗传算法、禁忌搜索算法.由于遗传算法(Genetic Algorithm，简称GA)是一种适合求解带有多变量、多参数、多目标和多区域但连通性较差的智能优化算法，因此本文考虑用遗传算法来解决排课问题，但是遗传算法具有早熟现象，并且很快收敛到局部最优而非全局最优解，所以结合了局部搜索方法之一的禁忌搜索算法(Tabu Search，简称TS)，即用遗传算法结合禁忌搜索算法来解决大学排课问题.

1 排课问题的算法设计

1.1 排课问题的双目标分析

(1)班级课时日分布优度的计算

这个指标主要是均匀分布班级每日的课时，班级日分布优度为:

式中td表示Bi班级在d个工作日所上的课的节次数;n则表示一周内的工作总天数.全校课时分布均匀程度可以用全校所有班级的课时日分布优度平均值来评价.

(2)班级日组合优度的计算

该优度重点用来表示班级课程组合的优劣，可以用全校所有班级的所有非2学时的课程的日组合优度的平均值来衡量.

式中，ki表示日组合优度;非2学时课程总数用n表率;m则表示全校班级总数.

1.2 排课问题的GATS算法设计

(1)GA编码

本文采用混合式教师编码，将它设定为遗传算法的基因.基因由班级序号、教师号、课程号、课程特点组成.其中用六位表示教师号，用一位表示班级序号，指该教师教的第几个班级.用一位表示课程序号，表示教师教的第几门课程.用三位表示课程特点，用于表示课程的类型，通过这样的编码［4］，解决了特定时段教师课程安排和有效分配.系统如果想要得到完善的课程表，则只要按照算法对编码进行各类处理即可.染色体编码就是把25个时间片(一般大学的课程工作日从周一到周五，一天最多有十节课:上午4节，下午4节，晚上2节，上课方式为一个课次两个相邻小节，所以设定一个课次为一个时间片，一天就可划分为5个时间片.这样总共一周可划分为25个时间片)的基因串组成一个染色体.

我们可以构造一个三维矩阵，其中时间片用横坐标表示，纵坐标表示教师、课程和教室，而Z坐标表示的是班级，如图1所示.

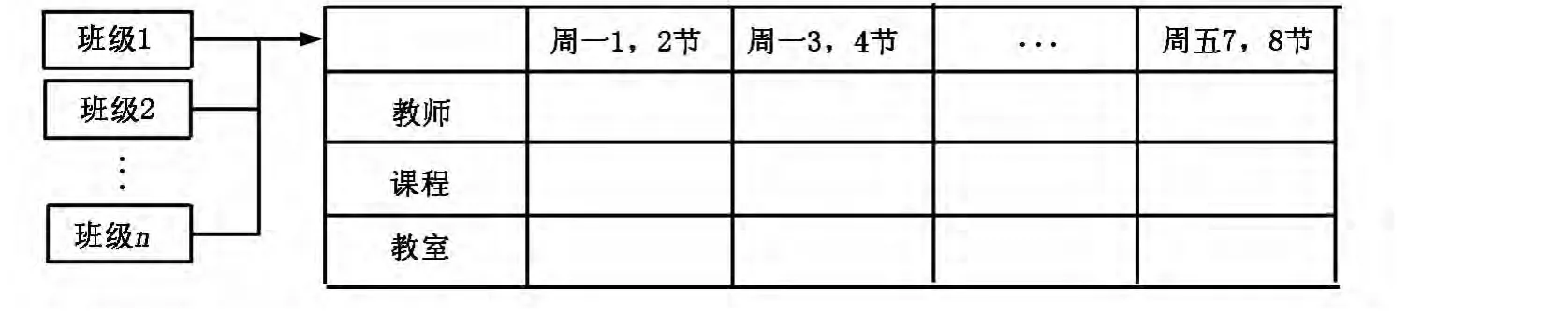
图1 染色体编码

(2)产生初始群体及消除冲突

本文采用的是对随机生成的初始群体进行调整，使它产生一组没有教室冲突的个体作为初始群体，同时，将教室利用率作为考查排课系统有效性的一个重要指标，通过教室利用率P扩大10倍转为适应度值参与进化计算.

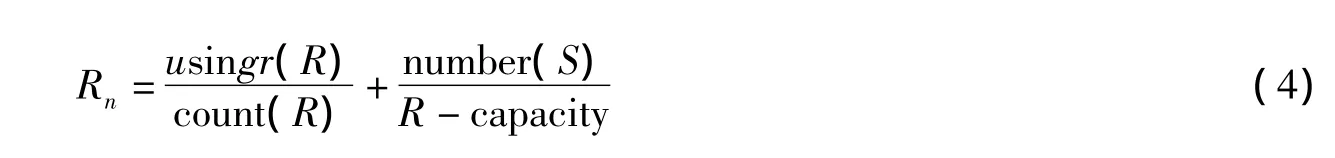
其中教室占用数量用usingr(R)表示，上课学生总数用number(S)表示.

在GA运行中，冲突在交叉和变异都可能产生，通过引入负的适应度值来降低冲突个体被选入的概率，还能将未消除的冲突记录下来，并在下次迭代中进行消除;对时间段冲突的两个个体，也可以用一个个体的冲突时间段与其空时间段互换来消除冲突［5］.

(3)定义和计算适应度函数

通过分析前面的双目标，采用如下的适应度函数

e为组合可行度，它只取0、1.管理人员自行定义K1、K2，代表目标的重要程度.当然，如果需要的话还可以再加入其他的目标.如何加快算法收敛的速度?运行中每一代产生的冲突将进行不完全消除，作为第三个条件，我们可以定义一个负的权值与其相对应.

(4)GA的运行

遗传算法主要分为选择、交叉、变异三个基本操作.

①选择操作

本文采用轮盘赌选择法种群下一代个体的选择.传统的遗传算法存在初始种群分布不均匀的现象，所以本文先把解空间划分n个区域，然后再分别对每个区域进行遗传的选择操作，最后再合并这些区域，从而实现种群的均匀分布.同时采用上一代和新生代最优个体类替换新生代的最差个体.这样便可以保证从遗传操作开始，新生代中都有目前为止最优的个体.

图2是轮盘赌选择示意图，其百分比表示的是被选中区域的概率.

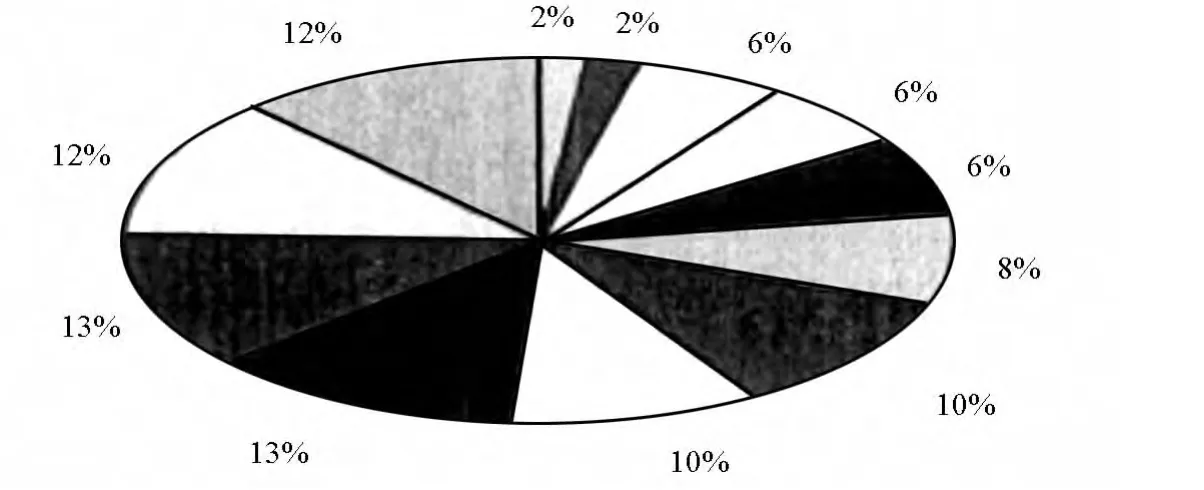
图2 轮盘赌选择

②交叉操作

交叉操作使用部分匹配交叉法，为了确定一个匹配段，它要求随机选择两个交叉点.即首先随机在两个父代个体中选择一个交配区域，如:

P1=123|456|7890 P2=674|321|5980

对两个父代交配区域进行交换，将无交配区不重复的保留，重复的用X记，得:

P1=＊＊＊|321|7890 P2=*7*|456|*980

根据交换位的对应关系用对应的值代替子代X的值，从而得到:

P1=654|321|7890 P2=173|456|2980

这种方法最大好处是可以满足染色体中没有重复基因编码的约束［6］.调整选课学生人数和教室座位人数间的冲突是交叉算子的首要作用.本文通过两个个体中对应班级的互换来完成交叉操作，首先按相同规则排序每个排课方案，接着对选择操作形成配对库，随机两两配对新复制产生的个体，最后对个体随机配对按预先设定的交叉概率来决定每对是否需要进行交叉操作，若需要，就进行交叉产生新位串.交叉算子操作如图3所示.

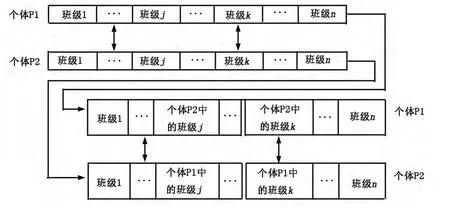
图3 交叉算子操作

③在变异阶段用传统GA进行排课的不足

GA变异操作以一定的变异概率随机找到某一行中的两个排课单元，交换它们的位置，判断它们是否满足教室与课程的冲突，如冲突则重新选择直到不冲突为止，这样不会违反与教室相关的硬约束［7］.变异形式如下:

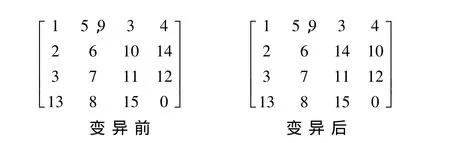
传统的GA会造成算法“局部收敛”而非得到全局最优解的原因是:GA具有“全局”搜索能力，如果进化世代中有个体适应度过高，使其被选择复制的概率变大，从而使其后代过多以及近亲繁殖.因此，对个体以变异概率进行变异操作成为必须，这在变异率的选择上就成了GA算法解决排课问题的关键.

④结合TS的变异操作

变异算子主要是使个体呈现多样性，而对于二进制编码，往往采用一个小的变异概率，通过随机翻转某些位来实现.由于TS算法有灵活的记忆功能和藐视准则，可以得到更优个体解，同时跳出局部最优［8］，因此我们用TS来代替变异算子.而对于排课问题，因为约束条件相互制约，是无法实现随机翻转的，所以本文在变异阶段用到禁忌搜索算法.

TS的领域定义为相邻两次课，我们把每个时间片的相邻时间片设为四，把每天的头尾两次课定义为相邻，把一周的头尾也定义为相邻.由此，从周一到周五进行1到25编号后，领域集可定义如下:

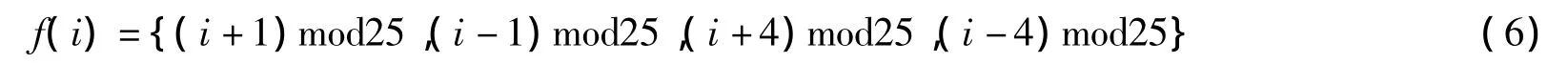
很明显每个班级课程数P的领域集为4P个，我们可以提取最佳的p个解做为候选解集.禁忌表长度设为6，算法结束条件为k次迭代.TS运行中也要一个概率.

⑤GA与TS相结合的流程

为了使群体中的个体分布在解空间的大部分区域，可先用GA进行全局搜索，把可能的排课情况都搜索出来，再用TS算法从群体中每个个体课表进行局部变异搜索，改善群体的质量.下面给出整体结合的算法流程:

步骤1:给定群体规模、最大迭代次数、交换概率、最熟识别等初始参数.

步骤2:确定编码方式，将t，c，k初始化为0.(t为当前迭代次数，c用来识别最熟现象，k为循环次数).

步骤3:随机产生初始群体，生成N个个体，令XB=第一个个体.

步骤4:将群体中每个个体适应值计算出来，设第一个个体为该代适应值最大的个体.

步骤5:若XB=第一个个体，则设c=c+1;否则将第一个个体值赋给XB，并设c=0.

步骤6:若c＞最熟识别参数，将个体按适应值从大到小排列，并按比例复制一部分个体到下一代，其余个体百分百变异，由此产生新一代个体，转到步骤8;否则转到步骤7.

步骤7:选择操作.

步骤8:交换操作.

步骤9:传统GA变异操作.

步骤10:若k=10，调用TS变异操作，改进群体点质量，并设k=0;否则转到步骤11.

步骤11:如果t＜T||当前时间未超时，设t=t+1，k=k+1，转到步骤4;否则进入步骤12.

步骤12:判断终止准则.

算法的终止准则:

(1)能接受的优秀个体被找到.

(2)达到了预定进化代数.

(3)在前后代数中适应值最高的个体适应度无改进.

(4)最适应个体占群体比例达到预定的比例.

(5)当运行时间达到我们指定的最大时间时［9］.

本文是采用终止优先级原则，对(2)、(5)取短时优先原则，即哪个快就哪个先停，然后再从中判断是否有优秀个体存在.

2 实例研究

作者以某高校信息技术与科学专业的排课系统建设为例，阐述了遗传算法与禁忌搜索算法相结合在排课系统研究中的应用.

2.1 排课问题的数学描述

课表编排将时间、教师、学生和教室四者进行组合规划.

在该专业的排课问题中，需要考虑到五个因素，分别为:

班级集合:C={C1，C2，C3，…，Cnc}

课程集合:L={L1，L2，L3，…，Lnl}

教师集合:T={T1，T2，T3，…，Tnt}

时间集合:P={P1，P2，P3，…，Pnp}

可排课的第i个时间段用Pi类表示，如P1表示周一1、2节、P10表示周三3、4节.

教室集合:R={R1，R2，R3，…，Rnr}

排课问题的解空间由笛卡尔积L×C×T×P×R的五个元素构成，排课问题也可以表示为映射:L→P×R，即为每门课找一个合适的时间和教室.

(1)排课中约束的描述

一个班级在同一时间只能安排一门课.

设 CLi表示 Li这门课的班级主体，设 f(Lm)=(Pxm，Rym)，f(Ln)=(Pxn，Ryn)且 m≠n，则当

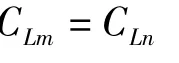
必有

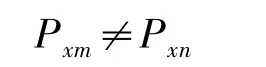
一个老师在同一时间也只能安排一门课，当然，一个教室在同一时间也是只能安排一门课程.表示方式均同上.

教室总数要求大于同一时间安排的课程总数.

设 f(Lm［i］)=(Pxm［i］，Rym［i］)，且 Pxm［1］=Pxm［1］=Pxm［n］，同时设 count(R)表示全校教室可用数，则count(R)≥n.

教室容量必须满足上课学生人数.用Ri－capacity表示Ri教室所能容纳的学生数.CLi－number表示Li这门课对应班级学生人数.如果 f(Lm)=(Pxm，Rym)，则 CLm－count≤Rym－capacity.

(2)排课中的优化解模型

在排课问题中，我们假设有n个决策变量参数、m个目标函数和p个约束条件，目标函数约束条件和决策变量间是函数关系，则排课最优化目标如下:

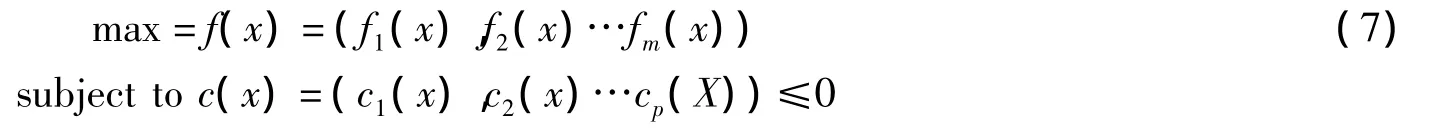
其中 x=(x1，x2，…，xn)∈X，y=(y1，y2，…，yn)∈Y

决策向量用x表示，优化目标向量用y表示，X，Y分别表示各自的目标空间，c(x)决定了决策向量的取值范围，反映了排课问题中的编排规则.

2.2 总体目标

本文通过对排课的目标要求和数学模型进行分析，认为应该分为两部分来求解.(1)我们把排课前已经定好把教师、班级、课程这三个因素绑定为一个整体，作为一个元组，并对这个元组随机分配时间和教室，生成可行课表;(2)运用遗传算法对排课问题进行编码，用基因和染色体方式表示排课中的各个变量，通过复制、交叉、变异的优化设计，计算出适应度函数.而TS主要用来代替遗传算法中的变异因子，从而得到比单纯用遗传算法更优的个体解，同时跑出局部最优，产生新的具有更优结构的个体，最终生成有效的课表.结果如图4所示:

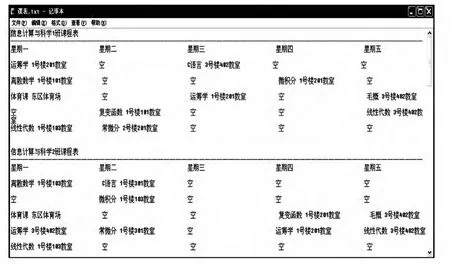
图4 生成课表

3 结束语

本文对遗传的染色体采用了一种较新的编码方式，针对排课问题的复杂性，本文提出了一种双目标的适应值计算方式，并有效地在初始种群的产生上进行了均匀化设计.由于遗传算法本身存在的一些不足:过早的局部收敛，因此采用禁忌搜索算法来代替遗传算法中的变异因子，设计了遗传禁忌搜索算法来解决排课问题.通过测验和使用，证实了在系统的操作性和搜索速率上，运用本算法有了明显的提高;数据分析也显示该算法能很好地完成预期要求，且结果令人满意.

由于课表问题具有规模大、约束条件复杂、需求不断变化等特征，本文在排课算法的完善方面还有很多需要努力的地方，如不规则周次课程的处理、异常状况突发的处理、排课结果的输出方式以及对算法复杂度的进一步缩小等.今后，在解决排课问题中，本人将更多地考虑研究多算法的融合，并将其定为一个主要的研究方向，继续努力.

［1］赵 辉，秦维佳.基于资源匹配的一种大学排课方法［J］.沈阳工业大学学报，2001，(4):342～344.

［2］李志强，赵卫东.排课问题的实现策略与模型［J］.泰山学院学报，2004，(6):61～64.

［3］王 璐，邱玉辉.基于协商的智能排课系统的研究［J］.计算机科学，2006，33(6):214～217.

［4］王 力.高校通用排课管理信息系统设计与实现［J］.贵州工业大学学报，1999，28(1):87～90.

［5］Alan Dix，蔡利栋，方思行译＞人机交互［M］.北京:电子工业出版社，2006.

［6］S.Daskalaki，T.Birbas.Efficient solutions for a university timetabling problem through integer programming［J］.European Journal of Operational Research，2005，160(1):106 ～120.

［7］D.Abramson.Constructing School Timetable using Simulated Annealing［J］.Sequence and Parallel Algorithm.Management Science.1991，37(1):98～113.

［8］清华大学计算机与信息管理中心.清华大学综合教务系统简介［R］.2005:96～98.

［9］王书振.改进遗传算法在调度领域中的应用［D］.西安:西安电子科技大学，2003.