Critical Length of Double-Walled Carbon Nanotubes Based Oscillators*
2014-04-24WangLifeng王立峰LiuRumeng刘汝盟
Wang Lifeng(王立峰),Liu Rumeng(刘汝盟)
State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University Aeronautics and Astronautics,210016,Nanjing,P.R.China
1 Introduction
Cumings and Zettl[1]created a system that one end of a multi-walled carbon nanotube(MWCNT)was opened and a core tube was pulled out from the outer shell.And they found that the core tube retracts into the outer shell when the core tube is set free.Zheng and Jiang[2]reported that the core tube would oscillate with gigahertz frequency if both ends of the outer shell are opened.They estimated the frequency of the oscillators through the restoring force obtained from the retraction potential.Since it is very hard to observe this interesting phenomenon through experiment,molecular dynamics(MD)simulations were carried out for these systems by several groups[3-7].
The van der Waals(vdW)potential energy between a carbon atom of inner tube and all the carbon atoms of outer tube depends on the relative position between this atom and the closest hexagonal unit of the outer tube[2].Charlier and Michenaud[8]calculated the potential barrier of a(5,5)/(10,10)double-walled carbon nanotube(DWCNT)using the local density approximation(LDA).They found that potential barrier per carbon atom for sliding motion is anisotropic.Satio et al[9]examined the adiabatic potential of a DWCNT for a variety of sets of inner and outer nanotube chiralities.Their results showed that the potential barrier for the relative displacement of the inner and outer tube layers depends significantly on the chirality difference of the pair.Guo and Gao[10]found that the energy dissipation related fluctuation of interlayer interaction forces can vary significantly with the chirality,length and diameter of the two tubes.The existence of potential barrier in sliding motion between inner and outer tube layers can give the reason that the inner tube cannot be pulled out from the outer tube with small force.Kimoto et al[11]calculated the force required to pull the inner tube out of the outer tube using MD method.They found the inner tube vibrates inside the outer tube instead of being pulled out,when the inner tube is subjected to a small constant force.These studies showed that the driving force due to the extrusion may be smaller than the force required to slide over the potential barrier of DWCNT-oscillators,if the coincidence length of inner and outer tubes is long enough.
In this paper,the critical lengths of the oscillators based on DWCNTs are studied by both theory and energy minimization simulation.The relationship between the vdW potential energy and lattice matching of the inner and outer tubes is gotten by pulling the inner tube under a constant step to determine the barrier force during sliding motion between inner and outer tube layers.The critical length can be obtained by setting the barrier force equal to the vdW restoring force.Then these results are compared with that calculated by the energy minimization simulations.The chirality matching effects and size effects are analyzed.Finally,the critical lengths of zigzag/zigzag oscillator system with different temperature are discussed using MD method.
2 Simulation models
2.1 Van der Waals restoring force
The restoring force resulting from asymmetry vdW interaction between inner and outer tubes due to the extrusion is the driving force for an oscillator based on MWCNT.
The excess vdW potential energy U due to extrusion is[12]

where a=0.142nm is the bond length between carbon atoms,Dis the diameter of the inner tube,LIand LOare the lengths of the inner and outer tubes respectively,ζis the separate distance between the centers of the inner and outer tubes.The vdW potential energy between a carbon atom of inner tube and all the carbon atoms of the outer tube is denoted by-Π.
The vdW restoring force can be obtained as follows[12]
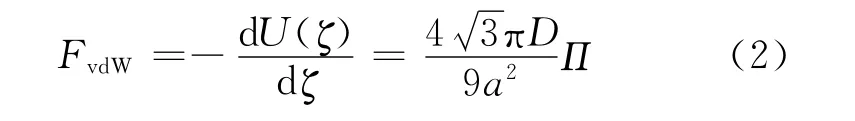
FvdWis a constant force if the separate distanceζ of a DWCNT-based oscillator is much larger than cutoff length of vdW potential.
2.2 Interatomic potential
In energy minimization simulations,the reliability of the results depends on the potential used in the carbon system.The Brenner′s secondgeneration reactive empirical bond order(REBO)potential[13],which has been widely used to describe mechanical properties of carbon nanotubes and graphene,is applied to describe the covalently bonded pair among atoms.
The following Lennard-Jones(LJ)potential is used to describe the vdW potential energy between atoms i and j belonging to different tubes

where well-depth energyε=4.748 3×10-22J and equilibrium distanceσ=0.34nm.In Eq.(3),rijis the distance between atoms i and j.
The vdW potential energy for the entire DWCNT is evaluated by summing Eijover all inter-tube i,j-pairs

2.3 Models for calculation of potential barrier
In order to determine the relationship between the vdW potential energy and lattice matching of the inner and outer tubes,a DWCNT model are constructed by placing two singlewalled nanotube models coaxially in xdirection as shown in Fig.1.The inner tube with periodic boundary condition is shifted 1×10-4nm every step along xdirection for 10 000steps,as shown in Fig.1.The total potential energy is monitored.(In order to neglect the edge-edge interaction,the distance between the inner and outer edges is taken to be larger than the cutoff length.)

Fig.1 DWCNT atomic model
2.4 Energy minimization simulation
In order to eliminate the influence of thermophoretic force,the simulations need to be conducted under very low temperature.However,a nonequilibrium finite temperature system is difficult to be treated by MD simulations.There have been no reliable simulation tools for such problems,so far.So energy minimization of this system with a damped dynamics method described by Bitzek et al[14]is adopted to simulate the inner tube retraction process.The velocity of each atom is initialized to be zero at the beginning of the minimization in this method.
A DWCNT with inner and outer tubes of the same length is modeled.The inner tube is pulled out from the outer one while the coincidence length of these two tubes is L1as shown in Fig.2.Then the potential energy of this system is minimized.

Fig.2 DWCNT for energy minimization
3 Results and Discussion
3.1 Zigzag/zigzag system
A(9,0)/(18,0)zigzag/zigzag system with the length LO=23.86nm is used to obtain the vdW potential energy barrier.The interlayer gap between inner tube and outer tube is 0.34nm.
For convenience,the vdW potential energy at the initial position is set to be zero.The relation-ship between the vdW potential and lattice matching of the inner and outer tubes are presented in Fig.3.It can be seen that vdW potential energy varies periodically with the relative position between the inner and outer tubes.The barrier force in Fig.4is obtained by the differential of the vdW potential energy with x.

Fig.3 Relationship between the vdW potential and lattice matching of inner and outer tubes for(9,0)/(18,0)zigzag/zigzag system

Fig.4 Barrier force of(9,0)/(18,0)zigzag/zigzag system obtained from the first-order derivative of the curve in Fig.3
Fig.4shows that the maximum value of the barrier force is Fmax=2.14nN.It means that at least 2.14nN is needed to move the inner tube if the coincidence length of(9,0)/(18,0)zigzag/zigzag system is 23.86nm.Same as the amplitude of total vdW potential energy shown in Fig.3,the barrier force is proportional to the coincidence length.Let the barrier force be equal to the restoring force in Eq.(2).

where k=Fmax/LOis the maximum barrier force per unit length.Then the critical oscillation length 10.48nm can be obtained from Eq.(5).
Energy minimization method is used to verify the result.As shown in Fig.5,the inner tube is pulled out from the outer tube.The initial coincidence length between inner tube and outer tube,i.e.L1,is 5nm.The vdW potential energy,which decreases with increasing of L1,is recorded during this process.The tendency of vdW potential energy in the minimization process is plotted in Fig.6,where the straight line represents the value of vdW potential when the inner and outer tubes coincide completely,and it is set to be zero for convenience.The vdW potential energydecreases during 0ns to 3ns generally.It stops at a certain value which is significantly larger than the value of vdW potential energy when the inner and outer tubes coincide completely.The inner tube retracts into the outer tube during the minimization process and stops when the coincidence length L2is 9.85nm.This critical oscillate length is close to the result predicted by Eq.(5).

Fig.5 Initial and equilibrium positions in the energy minimization for(9,0)/(18,0)zigzag/zigzag system
The critical oscillate lengths of zigzag/zigzag systems with different diameters obtained by theory and the energy minimization method are shown in Fig.7,where r is the diameters of the inner tubes.The interlayer gaps between inner tubes and outer tubes are kept 0.34nm.The critical oscillate lengths keep constant before the diameters of the inner tubes drop to 0.274nm.However,it will increase sharply if the diameter of carbon nanotube(CNT)is below 0.274nm.As shown in Fig.8,the cross section of a(n,0)CNT is a 2n-regular polygon which will no longer be close to a circular if nis not big enough.The smallest system we calculated is a(4,0)/(13,0)zigzag/zigzag system,and the cross section of the inner tube is nearly an octagon.The LJ potential energy distribution of this system is more complex than that of the circular case.The complex distribution of LJ potential energy leads to a sharp increasing trend in the small diameter region calculated by energy minimization method.The theory results are in good agreement with the energy minimization results if the diameter of the inner tube is big enough.The restoring force in Eq.(2)is obtained using an alternative approach by replacing the discrete distribution of atoms on the outer shell with a continuous distribution of the same atom density4a2[12],which will invalidate if the diameters of the system are small.So the deviation between the theory and the energy minimization method becomes larger when the diameters of the system are smaller.

Fig.7 Critical oscillate lengths of zigzag/zigzag systems with different diameters

Fig.8 Cross sections of CNTs with different diameters
3.2 Armchair/armchair system
Next a(5,5)/(10,10)armchair/armchair system is considered.Atomic model with coincidence length 30nm shown in Section 2.3is built.The vdW potential energy which is also set to be zero at the initial position is plotted in Fig.9.Fig.10shows that the maximum barrier force is 0.157nN when the coincidence length is 30nm.The critical length obtained by Eq.(5)is 175nm.
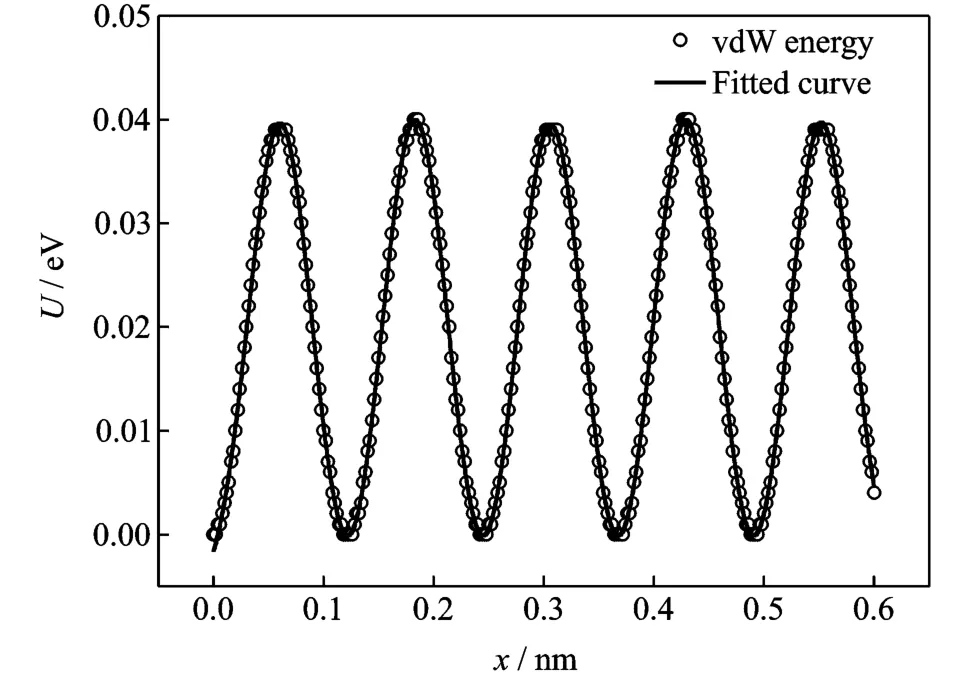
Fig.9 Relationship between the vdW potential and lattice matching of inner and outer tubes for(5,5)/(10,10)armchair/armchair system
A(5,5)/(10,10)armchair/armchair system being 200nm long with 48 900atoms is established to confirm the above result.As shown in Fig.11,the original coincidence length of inner and outer tubes is L1=160nm.The final coincidence length is 185nm after fully energy minimi-zation.

Fig.10 Barrier force of the(5,5)/(10,10)armchair/armchair system obtained by the firstorder derivative of the curve as shown in Fig.9

Fig.11 Initial and equilibrium positions in the energy minimization of(5,5)/(10,10)armchair/armchair system
These above two systems have similar diameters,which means the restoring force of these two systems is very near.But the vdW potential energy fluctuation of zigzag/zigzag system is much higher than that of armchair/armchair system.It is thus easier to slide over the barrier of the armchair/armchair system for the same restoring force.So the critical length of(5,5)/(10,10)armchair/armchair system is much larger than that of(9,0)/(18,0)zigzag/zigzag system.
3.3 Temperature effects
The effects of temperature for the critical oscillate length are studied by MD simulations with Nose-Hoover feedback thermostat[15-18].The velocity-Verlet algorithm with time step 1fs is used in the MD simulations.A(9,0)/(18,0)zigzag/zigzag oscillate system at different temperatures are simulated in the(N,V,T)ensembles by MD method.The inner tube is pulled out from the outer tube at the beginning of simulations.All the atoms are kept free during simulations.It is found that the inner tube retracted into the outer tube for a certain length.The inner tube may revolve around x axis during the retraction process.Fig.12shows that the critical lengths increase along with temperature.Atoms with higher temperature are far away from equilibrium.So their vdW energy is higher than those with lower temperature[19].And it is easier for atoms with higher temperature to slide over the vdW potential barrier.
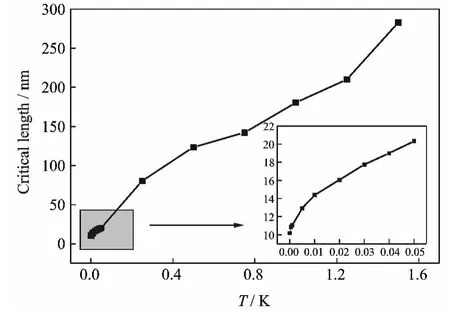
Fig.12 Critical oscillate lengths of(9,0)/(18,0)zigzag/zigzag systems at different temperatures
But the temperature discussed here is very low.We must simulate in a larger system for the higher temperature which is out of our computational ability.The MD method based on classical Newtonian mechanics does not allow for the description of quantum effects which may play a key role in high-frequency oscillations at such low temperatures.Some MD methods with quantum effects taken into consideration should be developed to give a better simulation to oscillators of DWCNT at such low temperature.
4 Conclusions
The critical length of a DWCNT-based oscillator is studied in this paper.The vdW potential energy changes periodically with the lattice matching of the inner and outer tubes.If the coinci-dence length is long enough,the restoring force is not big enough to slide over the vdW barrier.The inner tube cannot retract into the outer tube.The critical oscillate length is predicted,and then confirmed by energy minimization method.Moreover,the amplitude of vdW potential energy fluctuation of armchair/armchair system is smaller than that of zigzag/zigzag system.The critical length of armchair/armchair system is much larger than that of zigzag/zigzag system.The critical lengths of zigzag/zigzag DWCNT-based oscillator systems with different diameters are obtained both by theory and energy minimization method.The theoritical results agree with those of the energy minimization when the diameter of the inner tube is not very small.The vdW interaction between inner and outer tubes cannot be treated as homogeneous when the diameter of carbon nanotube is very small.So in such a case,the critical length strongly increases.Finally,the MD simulation is carried out to study the critical length of zigzag/zigzag system at different temperatures.Results show that the critical lengths of the DWCNT-based oscillator increase when temperatures rise.
[1] Cumings J,Zettl A.Low-friction nanoscale linear bearing realized from multiwall carbon nanotubes[J].Science,2000,289(5479):602-604.
[2] Zheng Q S,Jiang Q.Multiwalled carbon nanotubes as gigahertz oscillators[J].Physical Review Letters,2002,88(4):045503.
[3] Guo W L,Guo Y F,Gao H J,et al.Energy dissipation in gigahertz oscillators from multiwalled carbon nanotubes[J].Physical Review Letters,2003,91:125501.
[4] Legoas S B,Coluci V R,Braga S F,et al.Gigahertz nanomechanical oscillators based on carbon nanotubes[J].Nanotechnology,2004,15(4):S184-S189.
[5] Legoas S B,Coluci V R,Braga S F,et al.Molecular-dynamics simulations of carbon nanotubes as gigahertz oscillators[J].Physical Review Letters,2003,90:055504.
[6] Rivera J L,McCabe C,Cummings P T.Oscillatory behavior of double-walled nanotubes under extension:A simple nanoscale damped spring[J].Nano Letters,2003,3(8):1001-1005.
[7] Liu P,Zhang Y W,Lu C.Oscillatory behavior of gigahertz oscillators based on multiwalled carbon nanotubes[J].Journal of Applied Physics,2005,98(1):014301.
[8] Charlier J C,Michenaud J P.Energetics of multilayered carbon tubules[J].Physical Review Letters,1993,70(12):1858-1861.
[9] Saito R,Matsuo R,Kimura T,et al.Anomalous potential barrier of double-wall carbon nanotube[J].Chemical Physics Letters,2001,348(3/4):187-193.
[10]Guo W L,Gao H J.Optimized bearing and interlayer friction in multiwalled carbon nanotubes[J].CMES:Computer Modeling in Engineering and Sciences,2005,7(1):19-34.
[11]Kimoto Y,Mori H,Mikami T,et al.Molecular dynamics study of double-walled carbon nanotubes for nano-mechanical manipulation[J].Japanese Journal of Applied Physics,2005,44:1641-1647.
[12]Zheng Q S,Liu J Z,Jiang Q.Excess van der Waals interaction energy of a multiwalled carbon nanotube with an extruded core and the induced core oscillation[J].Physical Review B,2002,65:245409.
[13]Brenner D W,Shenderova O A,Harrison J A,et al.A second-generation reactive empirical bond order(REBO)potential energy expression for hydrocarbons[J].Journal of Physics:Condensed Matter,2002,14(4):783-802.
[14]Bitzek E,Koskinen P,Gahler F,et al.Structural relaxation made simple[J].Physical Review Letters,2006,97:170201.
[15]Nose S.A molecular dynamics method for simulations in the canonical ensemble[J].Molecular Physics,1984,52(2):255-268.
[16]Nose S.A unified formulation of the constant temperature molecular dynamics methods[J].The Journal of Chemical Physics,1984,81(1):511-519.
[17]Hoover W G.Canonical dynamics:Equilibrium phase-space distributions[J].Physical Review A,1985,31(3):1695-1697.
[18]Nose S.Constant temperature molecular dynamics methods[J].Progress of Theoretical Physics Supplement,1991,103:1-46.
[19]Guo Z R,Chang T C,Guo X M,et al.Mechanics of thermophoretic and thermally induced edge forces in carbon nanotube nanodevices[J].Journal of the Mechanics and Physics of Solids,2012,60(9):1676-1687.
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Aircraft Electric Anti-skid Braking System Based on Fuzzy-PID Controller with Parameter Self-adjustment Feature*
- Dry Grinding of Titanium Alloy Using Brazed Monolayer cBN Wheels Coated with Graphite Lubricant*
- Multi-objective Optimization of Differential Steering System of Electric Vehicle with Motorized Wheels*
- Compensation Algorithm Based on Estimation State for Transmission Delay in Cooperative Localization*
- Adaptive Angular Velocity Tracking Control of Spacecraft with Dynamic Uncertainties*
- Drag Reducing and Increasing Mechanism on Triangular Riblet Surface*
