Parameter Optimization Method for Gaussian Mixture Model with Data Evolution
2014-04-24YuYuecheng於跃成ShengJiagen生佳根ZouXiaohua邹晓华
Yu Yuecheng(於跃成),Sheng Jiagen(生佳根),Zou Xiaohua(邹晓华)
1.College of Computer Science and Engineering,Jiangsu University of Science and Technology,Zhenjiang,212003,China;2.Information Technology Research Base of Civil Aviation Administration of China,Civil Aviation University of China,Tianjin,300300,China
1 Introduction
Clustering analysis is one of the most important methods of data prediction and data analysis in the field of machine learning and data mining[1-2].According to measured or perceived intrinsic characteristics,the data set is partitioned into several clusters by the clustering algorithm,where the data points from the same cluster should be similar as much as possible,and the data points from the different clusters should be dissimilar[3].In general,data clustering has been used for the following three main purposes:disclosing the underlying structure of data set,realizing the natural classification of data points,and organizing the data or summarizing the data through cluster prototypes[4].Essentially,the above applications are used to find the potential patterns or data structure by clustering.
The conventional clustering algorithms focus on static data set,and assume that all data obey an underlying distribution which will not evolve along time[5].However,there are some that applications,such as dynamic social network[6-8],blog communities[9]and moving objects tracking[10],where the size of dataset or the data distribution may drift along time due to concept drifting or noise varying[5,11].In this case,the potential patterns implicated in dynamic data set cannot be accurately analyzed by using conventional clustering algorithms.
Evolutionary clustering is an extended application of clustering analysis.Its main purpose is to disclose the inherent patterns of data set and the evolutionary characteristic of evolving datasets.The existing evolutionary clustering algorithms typically outperform conventional static clustering algorithms by adding a temporal smoothness penalty to the cost function[12].The result of evolutionary clustering is a sequence of clustering in a time-line.For the clustering result produced during aparticular timestamp,two criteria including high snapshot quality and low history cost,should be met.This means that the sequence of clustering should have high-quality clustering at the current timestamp,and meet temporal smoothness in the successive timestamp[13].Now,several frameworks of evolutionary clustering have been proposed[4,11-15].Evolutionary k-means,proposed by Chakrabarti,et al is the first framework of evolutionary clustering.This framework adopts the objective function of k-means as the function of snapshot quality and the differences between all pairs of centroids in successive timestamp as the penalty of history cost.Its main weak point is that the stability of clustering cannot be guaranteed.As a result,the small perturbation on the centroids may cause drastic changes of clusters[11].Based on spectral clustering,Yun Chi,et al[11]proposed the other two frameworks of evolutionary spectral clustering,namely,preserving cluster quality(PCQ)and preserving cluster membership(PCM),where two different measure strategies of temporal smoothness were integrated in the overall measure of clustering quality.In the PCQ framework,the current partition is applied to historic data and the resulting cluster quality determine the temporal smoothness cost.In the PCM framework,the current partition is directly compared with the historic partitions and the resulting differences determine the temporal smoothness cost.From the measure strategy of history cost,PCQ is similar to evolutionary k-means,but PCM adopts the similar idea of constrained clustering[11].
Penalized likelihood is often used to learn the parameters of Gaussian mixture model(GMM)and has been used in regression analysis,classification and clustering etc.In the field of machine learning,conditional entropy and Kullback-Leibler divergence are the main measure strategies used to evaluate the differences of information and distributions[16].By introducing manifold learning into parameters evaluation of GMM,Laplacian regularized Gaussian mixture model(LapGMM)was proposed by He,et al[17].According to the idea of LapGMM,the nearby data points along the geodesics on the manifold have the similar conditional probability density functions.Based on the assumption,Laplacian regularization is defined to penalize the likelihood function and the conditional probability distribution of the nearby data points can be smoothened.Based on the similar idea,locally consistent Gaussian mixture model(LCGMM)was proposed by Liu,et al[18],where locally consistent assumption was adopted.
To most of the existing evolutionary clustering algorithms,the overall properties of data points between the corresponding clusters in successive timestamps are integrated into the definition of history cost function.This is beneficial to avoid the obvious fluctuation from the noise data points[13-15].However,the individual differences between data points are ignored.In fact,the different data points may have different effects on the evolutionary clustering when the data distributions drift.Inspired by LapGMM and LCGMM,evolutionary Gaussian mixture model based on constraint consistency(EGMM)is proposed from the point of view of constrained clustering.Using GMM as the model of data description,the snapshot quality function of EGMM is defined by means of the log-likelihood of complete data set,and the history cost function of EGMM is defined according to the differences between the posterior distributions.These distributions describe the statistic characteristics of all pairwise data points,which have the same cluster labels in the previous clustering results.
2 Notations and Related Work
The research objective of evolutionary clustering is to cluster the dynamic datasets,whereas evolutionary clustering also relates to the other research fields,such as data stream clustering,incremental clustering and constrained clustering[13,19].In this section,evolutionary k-means and evolutionary spectral clustering will be introduced based on the unified forms of notation representation.Evolutionary k-means is the first framework of evolutionary clustering,and the relation between evolutionary and constrained clustering has been firstly described in the framework of evolutionary spectral clustering.
2.1 Definition of notations
To obtain the smooth clustering sequence,the clustering results and data distributions at t-1timestamp should be integrated into the clustering process at t timestamp.So,the subscripts,namely″t″and″t-1″,represent the corresponding information at t and t-1timstamps,respectively.Let Xt= {xt,i}ni=1denote the data set at t timestamp,where nrepresents the number of data points.Correspondingly,let Xt-1denote the data set at t-1timestamp.The current data set consists of Xt(new)and Xt(old),namely Xt=Xt(new)∪Xt(old),where Xt(new)denotes the newly increased data set at t timestamp and Xt(old)denotes the joint data set at t and t-1timestamps.As the subset of Xt,Xt(old)may include all or part of Xt-1,namely Xt(old)⊆Xt-1.This includes the following two cases.If Xt(old)=Xt-1,it means that all data points at t-1timestamp will appear at t timestamp.Otherwise,only part of data points at t-1timestamp will appear at t timestamp,namely Xt(old)⊆Xt-1.Among them,the former can be regarded as a special form of the latter case.
Assume that Ktrepresents the number of cluster,and MCt={μt,k}Ktk=1the set of centroids,whereμt,kis the centroid of the kth cluster and the subscript″t″represents the t timestamp.We also use Ct,kto represent the data set of the kth cluster at t timestamp.Correspondingly,we assume that MCt-1={μt-1,k′}Kt-1k′=1represents the set of centroids at t-1timestamp,whereμt-1,k′denotes the centroid of the k′th cluster and Kt-1represents the number of cluster at t-1timestamp.The notation of Ct-1,k′is used to represent the data set of the k′th cluster at the t-1timestamp.
2.2 Evolutionary k-means
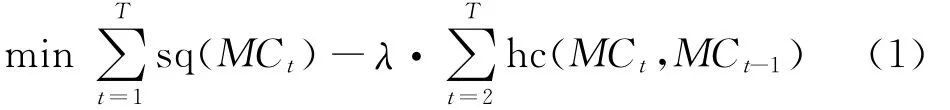
whereλis the tradeoff parameter of clustering quality and history cost defined by user.
On the online setting,the objective function of evolution k-means can be described
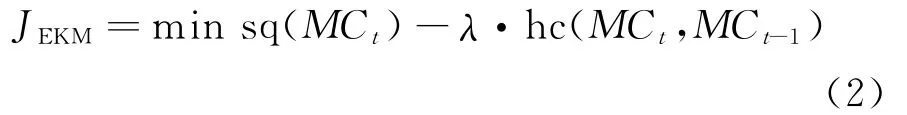
where the objective function of standard k-means is the snapshot quality function[13],namely
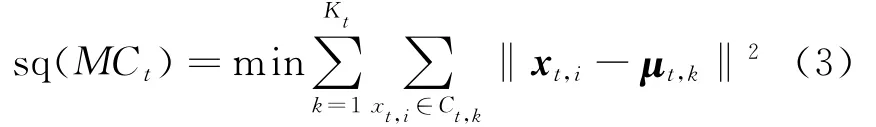
As the first framework of evolutionary clustering,the object of evolutionary k-means is evolving data points.Its goal is to obtain a smooth clustering sequence.In the framework,the clustering differences between adjacent time-stamps are measured by history cost function,denoted as hc(MCt,MCt-1),and the clustering quality of current data points is measured by the function of snapshot quality,denoted as sq(MCt).By minimizing the objective function Eq.(1),the clustering sequence with the optimal clustering quality can be guaranteed by performing the algorithm of evolutionary k-means[13].
In the framework of evolutionary k-means,history cost is measured by the distance sum of the pair of centroids,where the most similar two clusters are respectively from the adjacent timestamps and the distance between the two centroids is the shortest.Let f:MCt→MCt-1be the mapping defined in the set of centroids.These centroids are either fromt or t-1timestamp.Then,μt-1,f(k)∈MCt-1denotes the centroid that is the nearest centroid at the t-1timestamp from μt,k.That is to say,for allμt-1,a∈MCt-1,the equation of d(μt,k,μt-1,f(k))=min d(μt,k,μt-1,a)is true,where the notation of d(·)represents the Euclidean distance between two clusters.So,the pair of clusters,namely Ct-1,f(k)and Ct,k,are the most similar clusters.The history cost function of evolutionary k-means can be defined as Eq.(4)[13]
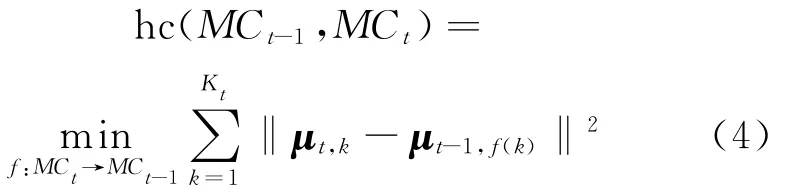
The algorithm of evolutionary k-means runs in an iterative manner adopted by standard kmeans.Eq.(5)is the updating formula of centroids.Its essence is to adjust the position of cluster centers at current timestamp using the historic centroids,where the corresponding historic cluster is the most similar to the current cluster.Then,the cluster centers at t timestamp will lie in between the centroids suggested by standard k-means and its closest match from the previous timestamp.With this mechanism,the better clustering quality and smooth clustering sequence can be guaranteed.
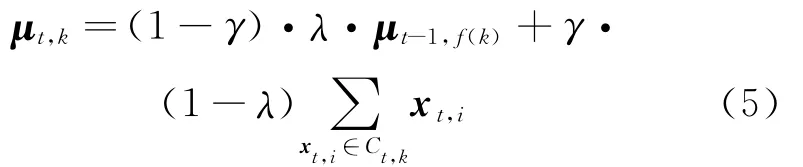
whereγ=|Ct,k|/(|Ct,k|+|Ct-1,f(k)|),|Ct,k|denotes the data number in Ct,kand|Ct-1,f(k)|denotes the data number in Ct-1,f(k).
History cost in evolutionary k-means is measured by the distance between each of the pair of centroids at t timestamp to its nearest peer at t-1timestamp.The sum of distance between all pairs of centroids is smaller,the differences of clustering results between adjacent timestamps are smaller too.Such a strategy of history cost has three weak points.First,the cluster number must be the same at adjacent timestamps.However,the dynamic data set will drift along time,this may cause the change of distributions.With in-depth understanding of the user,the concept may evolve too.These situations may result in changes of cluster number.Second,history cost is measured in the distance between the corresponding centroids.When the position of centroid changes slightly,the history cost may change drastically.This will affect the stability of clustering results[5,11,19].In addition,only the overall differences of data points at adjacent timestamps are considered,but the different effects from individual data points are ignored during the process of evolutionary clustering.
2.3 Evolutionary spectral clustering
Since the clustering results of evolutionary kmeans is not stable,two frameworks of evolutionary spectral clustering,namely PCQ and PCM,were proposed by Chi,et al[11].To measure temporal smoothness,two different fitting methods are adopted,including the one indicating how the current clustering results are consistent with the characteristics of historic data points or the historic clustering results[11,19].
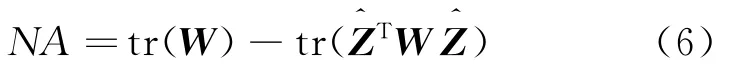
where tr(·)represents the trace of matrix.Assume that Wtand Wt-1represent the vertex similarity matrix at t and t-1timestamps,respectively,then the total cost function of PCQ can be defined as Eq.(7)[19]
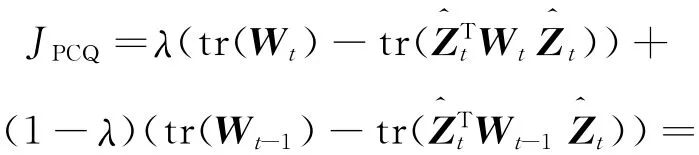
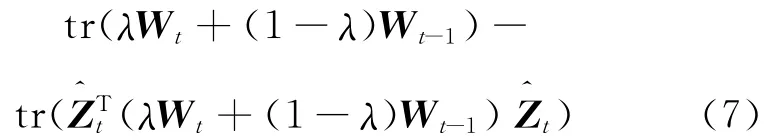
whereλ(0≤λ≤1)is the tradeoff parameter of clustering quality and history cost defined by user,andis the representation matrix of the partition at t timestamp.
For the objective function of PCQ,the first term,namely tr(λWt+(1-λ)Wt-1),is a constant,which is independent of the clustering partitions,minimizing Eq.(7)is equivalent to maximizing the second term of the objective function.Directly solving the objective function of PCQ is an NP-hard problem.Similar to most spectral clustering methods,one solution is to relax matrixto projection matrix Xt∈Rn×k,where the element values ofare discrete and the element values of Xtare continuous.Then,the problem of maximizing matrix trace is converted into solving the Keigenvectors associated with the top-K eigenvalues of matrixλWt+(1-λ)Wt-1.In the framework of PCQ,the current clustering result is used to fit the historic data points to guarantee temporal smoothness,so the vertex similarity matrixes of the current time-stamp and the previous timestamp are contained in the objective function simultaneously.The algorithm steps of PCQ is similar to the general spectral clustering,except that the weighted sum of matrixes Wtand Wt-1must be calculated when using eigenvectors to construct the projection space of data points.
Unlike the PCQ model,PCM uses the differences of partitions between adjacent timestamps to guarantee temporal smoothness.To achieve this goal,the representation matrixes,includingand,are relaxed to two projection matrixes Xt∈Rn×kand Xt-1∈Rn×k,respectively,whose elements are continuous.Then,the differences between two projection matrixes are norm.
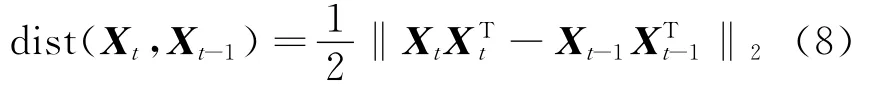
Furthermore,the total cost function of PCM can be defined as Eq.(9)[19]
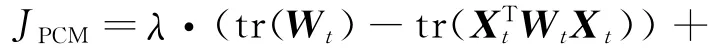
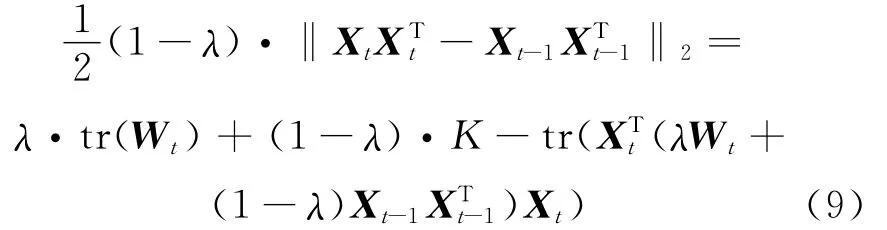
Similar to the PCQ model,PCM has the same steps of algorithm with the general spectral clustering,but the different matrixes are used during the process of constructing projection space by calculating the eigenvectors.By solving the Keigenvectors associated with the top-K eigenvalues of matrixλWt+(1-λ)Xt-1Xt-1Tto construct a vector space,the data points are projected into the space and evolutionary spectral clustering can be realized.Because the partition differences between adjacent timestamps need be compared,the projection matrix at the t timestamp includes the partition information from the projection matrix at the t-1timestamp in the framework of PCM.
3 Model of EGMM
3.1 Gaussian mixture model
To effectively deal with the evolving data set generated from independent and identically distributed(IID)samples from one underlying distribution,we can assume that all data points at each timestamp are from special distributions of GMM.Thus,from the perspective of modelbased clustering,evolutionary clustering becomes a mixture-density parameter estimation problem of dynamic GMM.We assume that the data set Xt= {xt,i}ni=1is generated from the parametric GMM model,where nis the data number of Xt.The probabilistic model can be defined as Eq.(10)[16]
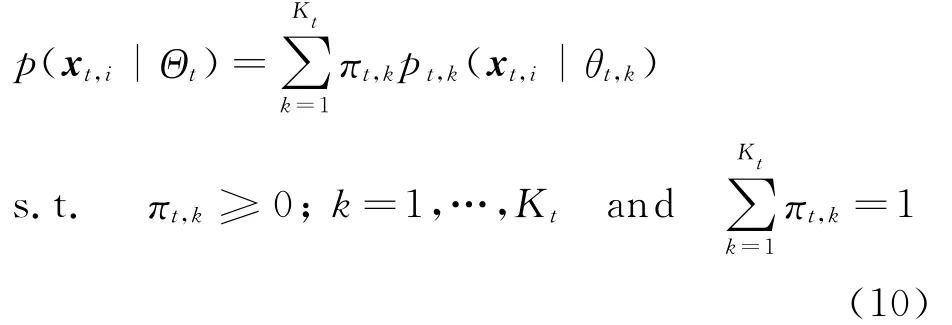
where xt,idenotes the i th data point at the t timestamp,Θt={πt,1,…,πt,Kt,θt,1,…,θt,Kt}the parameter set of GMM,Ktthe expected number of clusters at t timestamp,as well as the number of Gaussian components of GMM,πt,kthe priori probability of data points which represents the weight of the kth Gaussian component;and pt,k(xt,i|θt,k)aprobability density function parameterized by parameterθt,k={μt,k,Σt,k)},here,μt,k,Σt,krepresent the mean and covariance matrixes of the corresponding Gaussian component,respectively.
In evolutionary clustering scenario,the data point at the t timestamp should appear with the greatest probability in the current model from the perspective of model-based clustering.This method can guarantee the better clustering quality to be obtained.Simultaneously,from the perspective of constrained clustering,pair of data points,generated from the same Gaussian component at the t-1timestamp,should be partitioned into the same cluster with the greatest probability under the current parameters of GMM.This strategy will produce a smooth clustering sequence.In EGMM,better clustering quality can be obtained through the maximization likelihood method,and smaller history cost can be guaranteed depending on the adjustment of regularization operator.Regarding the clustering results at the t-1timestamp as prior,the regularization operator can be defined to adjust the parameters estimations of EGMM at the t timestamp.As a result,the pair of data points meeting aprior constraint can be assigned the same cluster with a greater probability.
3.2 Snapshot quality function
Assume that Yt={yt,i}ni=1is the set of unobserved data,whose values inform us which component density″generated″each data in Xt.That is to say,yt,i∈{1,…,Kt}represents that each data points xt,iis generated from the yt,ith Gaussian component.Thus,log-likelihood function of complete data set,namely log(L(Θt|Xt,Yt)),can be defined as[20]
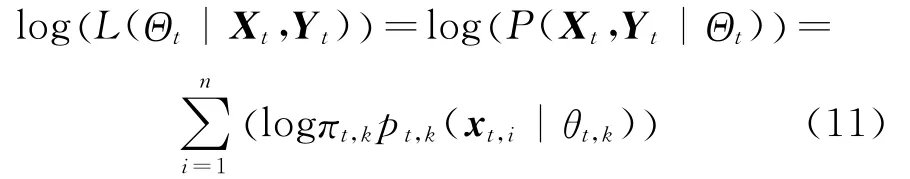
Essentially,the expectation of log-likelihood should be maximized to realize the evolutionary clustering in EGMM.The clustering quality at the t timestamp depends on the values of parameters estimations by maximizing the log-likelihood.Therefore,in Eq.(12)the expectation of log(L(Θt|Xt,Yt))is the function of snapshot quality of EGMM,whereΘgtrepresents the current parameters of EGMM at the t timestamp and θgt,kthe parameters of the kth Gaussian component at current iteration step.Correspondingly,the notations ofπt,kandθt,krepresent the parameters of the kth Gaussian component,which will be updated at current iteration step.

3.3 History cost function
Assume that Zt(xt,i)and Zt-1(xt,i)represent the cluster assignment at t and t-1timestamps respectively.If Zt-1(xt,i)=Zt-1(xt,j)is true,we can say that pairwise data points,denoted as(xt,i,xt,j),are generated from the same Gaussian distribution.According to the idea of constrained clustering,all pairwise data points can be regard as a prior knowledge at the t timestamp to smoothen the clustering.Such knowledge shows that pairwise data points,namely(xt,i,xt,j),may meet the constraints of″must link″.This means that for each xt,i,xt,j∈Xt(old),pairwise data points(xt,i,xt,j)should satisfy the constraint of″must link″if xt,i,xt,j∈Ct-1,k′is true.Thus,Ct-1,k′becomes the data set composed of pairwise data points.Since the equation Xt(old)=Ct-1,k′is true,the other equation Mt=Xt(old)will be true,where Mtis the constraints set of″must link″.
Assume that evolutionary data set obeys the IID assumption,and each data point of Xtis sampled according to the marginal distribution of Gaussian component.Since the correlation between marginal distribution and conditional distribution is based on the assumption of cluster consistency,if pairwise data points(xt,i,xt,j)meet the constraint of″must link″,the corresponding conditional distribution of xt,iand xt,j,i.e.,p(k|xt,i)and p(k|xt,j,Θgt),should be a great similarity[21].For simplicity,we use pt,i(k)and pt,j(k)as the substitutes for p(k|xt,i,Θgt)and p(k|xt,j,Θgt),respectively.To measure the difference between pt,i(k)and pt,j(k),we use(pt,i(k)‖pt,j(k))defined in Eq.(13)as a substitute for Kullback-Leibler(KL)divergence[18]
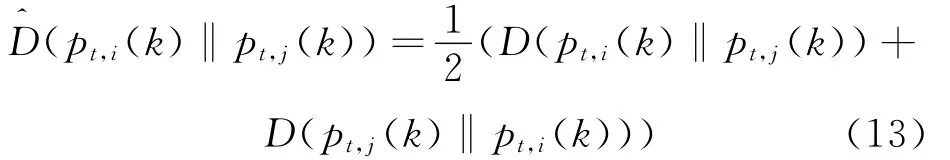
In Eq.(14),D(pt,i(k)‖pt,j(k))represents the KL divergence about pt,i(k)and pt,j(k)[16]
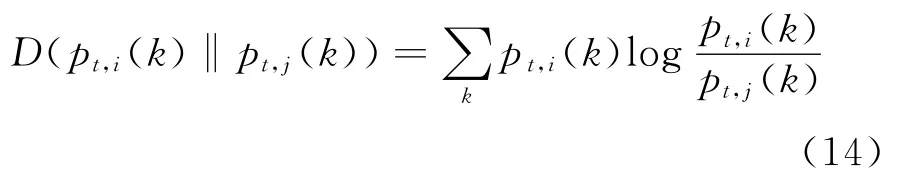
To smoothen the results of evolutionary clustering,pairwise data points that have the same cluster labels at the t-1timestamp should be partitioned into the same group as much as possible.To realize the goal,(pt,i(k)‖pt,j(k))defined in Eq.(13),is used to measure the differences between posterior distributions of pairwise data points during the process of evaluating parameters of EGMM.Intuitively,if(xt,i,xt,j)∈Mt,the value of(pt,i(k)‖pt,j(k))should be smaller,which can smoothen the corresponding posterior distributions and increase the probability that xt,iand xt,jare assigned to the same Gaussian component at the t timestamp.Thus,the cluster labels of all pairwise data points in Mtcan be used as constraint information.Then we define the function of history cost in Eq.(15).It minimizes the differences of posterior distributions of pairwise data points in Mt,and leads to the end that constraint violation occurs with a minimal probability in the estimation model at the t timestamp.
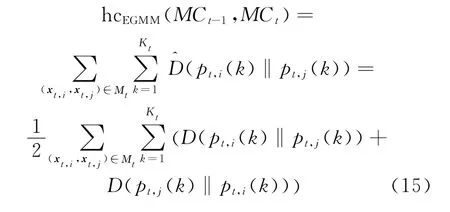
3.4 Objective function
According to Eqs.(12,15),the objective function of EGMM can be defined as
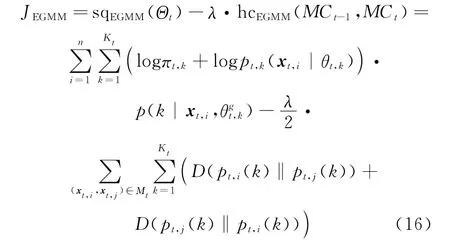
As an alternative form of KL divergence,(pt,i(k)‖pt,j(k))is nonnegative too.Maximizing the objective function is equivalent to performing the following two operations simultaneously,including maximizing the expectation of log-likelihood of the complete data set at the t timestamp and minimizing the differences between posterior distributions of pairwise data points in Mt.Thus,the clustering quality can be guaranteed by using the model of GMM to fit the current data points.Moreover,using the information of cluster labels from the previous clustering results,the clustering results between adjacent timestamps can be smoothened.
3.5 Model parameter fitting
The objective function of EGMM is a combined optimization function.Its maximization can be iteratively solved using the framework of expectation maximization(EM)algorithm.Similar to the standard EM algorithm,the posterior probability of xt,igenerated from the kth Gaussian component,denoted as pt,k(k|xt,i,Θgt),will be calculated according to the Eq.(17)in the E step.In the M step,Eq.(16)will be maximized,and the two goals,including maximizing the expectation of log-likelihood and minimizing the difference of posterior distributions,will be performed simultaneously.
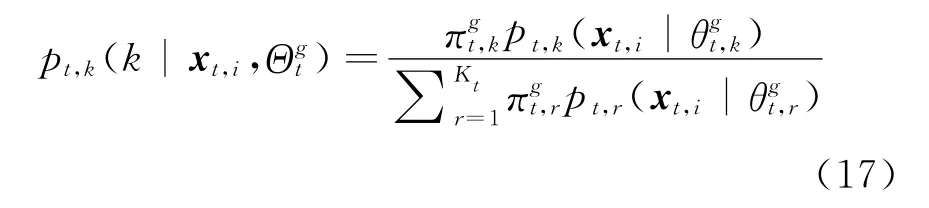
To maximize Eq.(16)in the M step,it needs to take the partial derivative of the combined function with respect to each parameter,and set it to be zero,then the iterative equations used to estimate the parameters can be obtained.The equations from Eq.(18)to Eq.(20)are the corresponding updating equations ofπt,k,μt,kandΣt,kof EGMM,whereπt,kdenotes the prior probability of data point generated from the kth Gaussian component at the t timestamp,μt,kthe sample mean,andΣt,kthe covariance matrix.
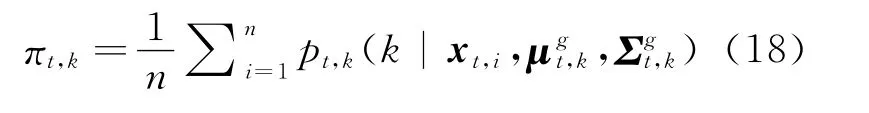
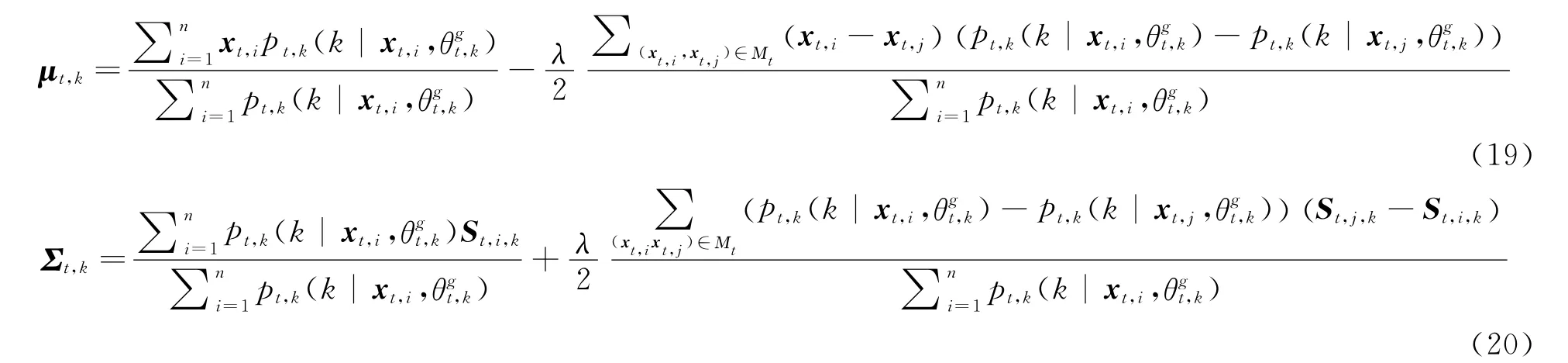
where St,i,k= (xt,i-μt,k)T(xt,i-μt,k),St,j,k=(xt,j-μt,k)T(xt,j-μt,k).
The following is the description of EGMM algorithm:
Input Input data set Xtand the expected number of clusters,denoted as Kt,at the t times-tamp;data set{Ct-1,k′from Xt(old)with the same cluster labels at the t-1timestamp and the corresponding parameter set{πt-1,k′, μt-1,k′,;regularization parameterλ.
Outpt Output parameter setΘt={πt,k,μt,k,and the value of objective function described by Eq.(16).
Method
(1)Initialization:In the 0th iteration step,if Kt-1≥Kt,randomly select Ktparameters from{πt-1,k′,μt-1,k′,Σt-1,k′as the initial parameter set,namely=;if,initialize={by performing k-means algorithm.
(2)To loop iteration until convergence:
(a)E step:In the lth iteration step,using the current parameter set={π,calculate the posterior probability pt,k(k|xt,i,)of each data point;
(b)M step:Sequentially update the parameter set={according to Eqs.(18-20)to prepare the(l+1)th step;
(c)If the convergence criteria are not met,go to(a);otherwise,terminate the loop.
To estimate the parameters of EGMM,the algorithm is performed by way of clustering evolutionary data,which is similar to the parameter estimation method of GMM.The difference between GMM and EGMM is that the previous clustering result is used to adjust the parameter estimation of EGMM.It is inspired from constrained clustering.However,it should be noted that constraint information used in EGMM comes from the previous clustering result rather than user provision.
In the E step,the same method is adopted by EGMM and EM algorithms to solve log-likelihood expectation.Hence,they have the same time complexity,namely O(nKtD3),where n is the number of data points,Ktthe number of Gaussian components of GMM,and Dthe dimension of data points.Because EGMM algorithm needs the previous clustering results to smoothen the estimation of current parameters,the corresponding time complexities to estimate each parameter in each step are O(nKt),O((n+|Xt(old)|)Kt)and O((n+|Xt(old)|)KtD),respectively.
4 Experimental Analysis
4.1 Datasets and measure criteria
To verify the effectiveness of EGMM algorithm,synthetic data sets and real data set,named the Columbia University Image Library(COIL),are adopted in this paper.For synthetic data set,the data are two-dimensional ones gen-erated from GMM.According to the evolutionary timestamps,the data sets are generated individually and contain 15timestamps altogether.Furthermore,the data set at different timestamps will vary in the size and data distribution.In addition,some noise data points are added.The dataset of COIL contains 1 044objects and each object is an image described by a 1 024-dimentional vector.During the process of the experiment,these objects are randomly divided into five subsets and each subset contains a number of objects of the previous timestamp.
The evolutionary clustering result is a timevarying sequence of clusters.At each timestamp,the clustering result needs to satisfy the two criteria:clustering quality and temporal smoothness.In this paper,clustering accuracy is adopted to assess the clustering quality.To evaluate the temporal smoothness of the clustering sequence,the fluctuation of history cost is compared.
4.2 Synthetic datasets
As shown in Table 1,the clustering accuracy of three algorithms including EM,evolutionary kmeans and EGMM are compared,which are per-formed on synthetic datasets at six timestamps,respectively.The data sets with noise data are generated from GMM,therefore the EM algorithm has the higher and more stable clustering accuracy.For this special synthetic datasets,its clustering accuracy is even higher than the clustering of evolutionary k-means.The foundation of evolutionary k-means is k-means algorithm,so satisfactory clustering results are difficult to be obtained for non-spherical datasets by running evolutionary k-means.From the stability of clustering results,agreater fluctuation often arises for the impact of noise data.As the evolutionary clustering version of EM algorithm,EGMM is still suitable for handing non-spherical datasets.By using the previous clustering results to adjust the parameters estimations,EGMM has the better performance to deal with the evolving datasets.Hence,the clustering quality is more stable than the other two algorithms and the algorithm is less sensitive to noise data.The results running on synthetic data sets show that the clustering results tend to be stable within a short time.

Table 1 Comparison of clustering accuracy on synthetic datasets(Acc)
The history cost of EGMM at each timestamp is demonstrated in Fig.1.The results running on synthetic datasets show that the history cost fluctuates within a short range,which means the clustering sequence of EGMM has better performance of temporal smoothness.
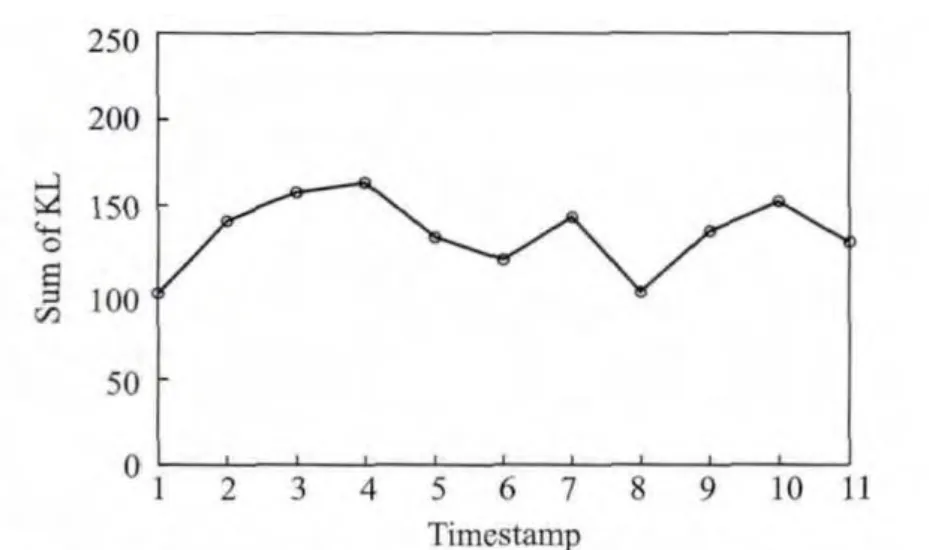
Fig.1 History cost of EGMM on synthetic datasets
4.3 Real datasets
To further validate the performance of EGMM,the dataset of COIL is divided into five subsets,then an evolutionary dataset that may drift at five timestamps is successfully constructed.It should be noted that all subsets at each timestamp contain a number of same or different samples to simulate the evolution scenario better.In Table 2,the clustering quality of three algorithms including EM algorithm,evolutionary kmeans and EGMM algorithm,is demonstrated,where the three algorithms are performed on the dataset of COIL at five timestamps.Compared with EM algorithm,the clustering results of EGMM better reflect the evolutionary features ofdata points by introducing historic clustering results;and compared with the evolutionary kmeans,EGMM can better fit the data features.The experimental results show that the evolutionary clustering framework of EGMM can obtain better clustering quality and realize the better data fitting in a short time.

Table 2 Comparison of clustering accuracy on COIL dataset(Acc)
In EGMM model,λis an adaptive parameter used to adjust the confidence of a priori.That is to say,different values ofλreflect different degrees of effects coming from the previous clustering results during the process of parameter estimation.In this paper,we adopt the approach by dynamically and adaptively selectingλ.Experiments show that several factors can affect the value ofλ,including the discrepancy between two distributions,the size of datasets and the number of joint data points at adjacent timestamps.
5 Conclusions
EGMM based on constraint consistency is proposed,which is closely related to the two technologies,i.e.,the constrained clustering and the evolutionary clustering.The basic idea comes from the constrained clustering,and the optimization method of model parameter needs to perform evolutionary clustering.From the feature of dataset,data points will evolve along time;and from the obtained clustering results,a clustering sequence with temporal smoothness must be guaranteed.The method thus belongs to evolutionary clustering.To guarantee the clustering quality at each timestamp and the temporal smoothness of clustering sequence,the previous clustering results are used as a priori constraints to adjust the parameter estimation and the assignment of data points.From this perspective,the method belongs to constrained clustering.
Compared with the existing constrained clustering algorithm,the a priori constraints come from the previous clustering results rather than the labeled data points.These a priori constraints can be obtained in a more natural way,and can reflect the internal structure of the data more truely.As the evolutionary algorithm,the algorithm of EGMM uses the overall differences and individual differences simultaneously to smoothen clustering results.Therefore the fluctuation of history cost becomes more stable.
As many other existing approaches,EGMM still has some limitations.For example,the adaptive parameterλis used to adjust the confidence of a priori,therefore,how to set it clearly according to previous clustering results is an interesting topic.To evolutionary clustering,the number of clusters may be changed with the evolution of data distributions,and then how to determine the number of Gaussian components becomes another interesting topic.Moreover,the method of EGMM can be used to handle various evolving data which evolves along time.Now,we are engaged in the analysis of air passenger behavior,which gradually evolves with region and age.
[1] Hand D,Mannila H,Smyth P.Principles of data mining[M].USA:MIT Press,2001.
[2] Wang Lina,Wang Jiandong,Jiang Jian.New shadowed c-means clustering with feature weights[J].Transactions of Nanjing University of Aeronautics and Astronautics,2012,29(3):273-283.
[3] Backer E,Jain A.A clustering performance measure based on fuzzy set decomposition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1981,3(1):66-75.
[4] Jain A K.Data clustering:50years beyond K-means[J].Pattern Recognition Letters,2010,31(8):651-666.
[5] Zhang J,Song Y,Chen G,et al.On-line evolutionary exponential family mixture[C]∥Proceeding of the 21st international joint conference on Artificial in-telligence.[S.l.]:Morgan Kaufmann Publishers,2009:1610-1615.
[6] Falkowski T,Bartelheimer J,Spiliopoulou M,et al.Mining and visualizing the evolution of subgroups in social networks[C]∥Proceedings of IEEE/WIC/ACM International Conference on Web Intelligence.[S.l.]:IEEE Computer Society,2006:52-58.
[7] Zhang Bo,Xiang Yang,Huang Zhenhua.Recommended Trust computation method between individuals in social network site[J].Journal of Nanjing University of Aeronautics and Astronautics,2013,45(4):563-568.
[8] Falkowski T,Bartelheimer J,Spiliopoulou M.Mining and visualizing the evolution of subgroups in social networks[C]∥Proceedings of IEEE/WIC/ACM International Conference on Web Intelligence.Hong Kong,China:IEEE Computer Society,2006:52-58,.
[9] Ning H,Xu W,Chi Y,et al.Incremental spectral clustering with application to monitoring of evolving blog communities[C]∥Proceedings of the 7th SIAM International Conference on Data Mining(SDM 2007).Minneapolis,Minnesota,USA:SIAM,2007:261-272.
[10]Zhang Chao,Wang Daobo,Farooq M.Real-time tracking for fast moving object on complex background[J].Transactions of Nanjing University of Aeronautics and Astronautics,2010,27(4):321-325.
[11]Chi Y,Song X,Zhou D,et al.Evolutionary spectral clustering by incorporating temporal smoothness[C]∥Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining(KDD 2007).[S.l.]:ACM Press,2007:153-162.
[12]Xu K S,Kliger M,Hero A O.Adaptive evolutionary clustering[J].Data Mining and Knowledge Discovery,2014,28:304-336.
[13]Chakrabarti D,Kumar R,Tomkins A.Evolutionary clustering[C]∥Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery And Data Mining(KDD 2006).[S.l.]:ACM Press,2006:554-560.
[14]Xu Tianbing,Zhang Zhongfei,Yu Philip,et al.Evolutionary clustering by hierarchical Dirichlet process with hidden Markov state[C]∥Proceedings of 8th International Conference on Data Mining(ICDM 2008).[S.l.]:IEEE Computer Society,2008:658-667.
[15]Ravi Shankar,Kiran G V R,Vikram Pudi.Evolutionary clustering using frequent item sets[C]∥14th International Conference of Knowledge-Based and Intelligent Information and Engineering Systems(KES 2010).[S.l.]:Springer,2010:11-20.
[16]Bishop Christopher M.Pattern recognition and machine learning[M].Singapore:Springer,2006.
[17]He Xiaofei,Cai Deng,Shao Yuanlong,et al.Laplacian regularized Gaussian mixture model for data clustering[J].IEEE Transactions on Knowledge and Data Engineering,2011,23(9):1406-1418.
[18]Liu Jialu,Cai Deng,He Xiaofei,et al.Gaussian mixture model with local consistency[C]∥Proceedings of the 24th AAAI Conference on Artificial Intelligence(AAAI 2010).USA:AAAI Press,2010:512-517.
[19]Chi Yun,Song Xiaodan,Zhou Dengyong,et al.Evolutionary spectral clustering[J].ACM Transactions on Knowledge Discovery from Data,2009,3(4):1-30.
[20]Bilmes J A.A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov mode[R].TR-97-021U.C.Berkeley,1998.
[21]Zhou Dengyong,Bousquet O,Navin Lal T,et al.Learning with local and global consistency[C]∥Advances in Neural Information Processing Systems 16(NIPS 2003).[S.l.]:MIT Press,2003:321-328.
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Development and Prospectives of Ultra-High-Speed Grinding Technology
- Threshold Selection Method Based on Reciprocal Gray Entropy and Artificial Bee Colony Optimization
- Optimal Power Management for Antagonizing Between Radar and Jamming Based on Continuous Game Theory
- Runge-Kutta Multi-resolution Time-Domain Method for Modeling 3DDielectric Curved Objects
- Semantic Social Service Organization Mechanism in Cyber Physical System
- Fast Numerical Solution to Forward Kinematics of General Stewart Mechanism Using Quaternion
