Optimal Power Management for Antagonizing Between Radar and Jamming Based on Continuous Game Theory

Wan Kaifang（万开方），Gao Xiaoguang（高晓光），Li Bo（李波），Mei Junfeng（梅军峰）

School of Electronics and Information，Northwestern Polytechnical University，Xi′an，710129，P.R.China

1 Introduction

Under the condition of information technology，the battlefield environment becomes increasingly complex.Hence，the competition between attacking and defending sides in the mastery of electromagnetic has been a new conflict intertwined point［1］.When a confrontation between radar and jamming occurs，the jamming side will take a full advantage of the synergetic superiority to suppress，disrupt and destroy the processes of early warning detection，target tracking and precision－guiding of enemy radar［2］.At the same time，the anti－jamming side will combine distributed radars to form a network for searching，tracking and identifying targets.The netted radars can gain detection range expansion and obtain better detection performance.

In order to effectively suppress the enemy radar network and improve the overall combat effectiveness，we need a reasonable allocation of va－rious jamming resources［3］.Meanwhile，the enemy side can also take similar measures to manage the radar resources［4－8］.Therefore，in the process of jamming and anti－jamming between radars and jammers，both sides should learn to choose a better strategy to maximize one′s own interests and minimize the opposite interests，thus bringing forth a game between the two sides.

Game theory is the one that the individuals or teams choose possible strategies synchronously or successively to achieve high payoff income according to the known information under a certain circumstance or constrained condition［9］.Game theory can ensure optimal decision for both sides whenever there is an interest conflict between the decision－makers in the same environment［10－12］.After fully considering the strategies that the opponent may take，the decision－making process of the game theory will be closer to the reality compared with the traditional decision－making methods that only take objective factors into account.Many scholars have been engaged in related researches on the modeling and application of game theory in decision－making field.Wei，et al［13］discussed a game theoretic target assignment in ballistic missile defense.Sang，et al［14］designed a midcourse guidance law for hypersonic cruise missile based on the differential game theory and neural network.Song，et al［15］investigated resource allocation problems using game theory.Game－based methods were discussed by Tang［16］and Song，et al［17］for multi－objective shape designing and multi－objective optimization，respectively.Yao，et al［18］presented a mission decisionmaking method for multi－aircraft cooperatively attacking multi－object based on game theory model，and Fu，et al［19］studied multi－UAV cooperative fight decision problems based on game theory.A differential game was used for the firepower－assignment in vessel formations by Li，et al［20］.Wei，et al［21］built a game－theoretic model for controlling military air operations with civilian players.Although game theory is more and more widely used in military，its application in power resource allocation for cooperative penetration combat has never been publicly reported.In this paper，after analyzing the nature of radar countermeasure，we propose a continuous game theory－based cooperative power management model to find an optimum allocation of power resources based on the opposite situation and the possible strategies of enemy side.

2 Problem Description

In a constantly changing situation，both opposing sides will effectively manage their own operating resources to pursue the more efficient operation［22－26］.

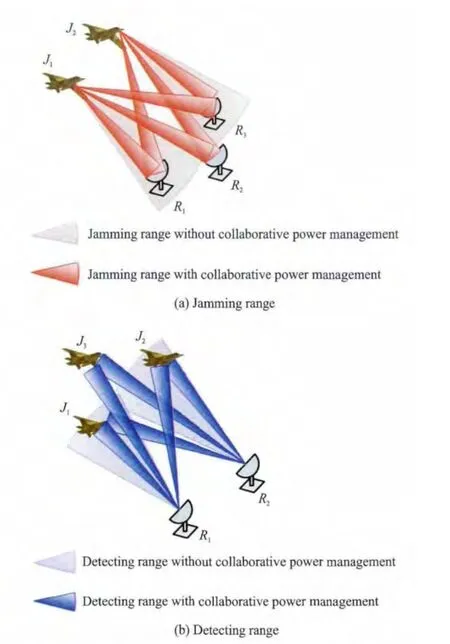
Fig.1 Maps of jamming and detecting ranges

Considering an offense－defense situation as shown in Fig.1（a），the blue side consists of three ground－based aerial defense radars，which form a radar network.The red side，in contrast，is composed of two fighters whose electronic countermeasures（ECMs）are turned on for self－screening jamming so as to guarantee the success of penetration.Suppose that there is no cooperation between two red fighters and both fighters release jamming signals separately only using their own energy.In Fig.1（a），radars R1and R3are adequately included in interference sectors，while radar R2is not.Meanwhile，the jamming regions of J1and J2overlap，which causes the waste of jamming energy and poor jamming effectiveness.If all the jamming power resources are scheduled and managed by an electronic warfare command center，the system can carry out a unified decision－making process.Then，the power resources will be distributed to the jammers reasonably according to the real－time situation，which can make full advantage of the multi－target jamming ability of ECM.Therefore，the overall operational effectiveness will be significantly improved.Accordingly，without coordination and collaboration of the detecting power resources，there will be a loss of overall detecting performance because of an ineffective usage of the limited power re－sources.Fig.1（b）shows that without an effective coordination，only J1and J2are covered by the detecting sectors of radars while J3cannot be effectively detected.Thus，it is necessary for both sides to precisely manage their own power resources in a radar－jamming counterwork.

2.1 Formulation of gaming

In offense－defense gaming between the red and blue sides，the goal is to seek a power allocation strategy that can maximize one′s own efficiency and minimize the opponent′s efficiency.Due to the infinity and continuum features of strategy set，the collaborative power allocation model for counterwork between radar and jamming can be modeled as a two－person general sum infinite continuous game model，namely

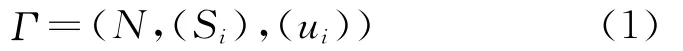
where Ndenotes the player set and N≜｛R，B｝，here“R”represents all fighters belonging to the red side and“B”all radars of the blue side.（Si）≜（SR，SB），where Sidenotes the strategy set of player i；and（ui）≜（uR，uB）is the payoff function of player i.

Suppose that the number of red fighters is m，the number of blue radars is n，and the total power of both sides are PJalland PTall，respectively.The gaming point is to deicide an optimal power transmitted from any fighter（radar）to any radar（fighter）.The decision variables are defined as

where xij（i＝1，2…m；j＝1，2…n）is the decision variable of the red side.Concretely speaking，xijmeans that the red fighter i will release a jamming with a power of xij·PJallto the blue radar j.Similarly，yij（i＝1，2…n；j＝1，2…m）indicates that the blue radar i will detect the red fighter j with a power of yij·PTall.DRand DBare the decision spaces that can be described as

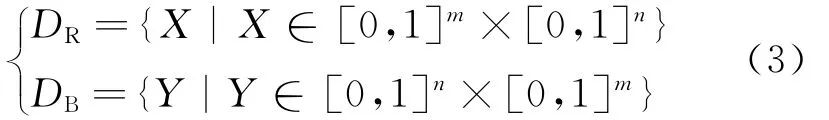
In the gaming process，the jamming side will suppress enemy radar to reduce its detection probability，while the radar side seeks a detection probability increase.Therefore，we choose the detection probability of netted radar as the payoff function［3］.According to the Neyman－Pearson criterion，when the probability density of radar receiver envelope detector obeys zero－mean Gaussian distribution，detection probability Pdand false alarm probability Pfof a single radar are defined as

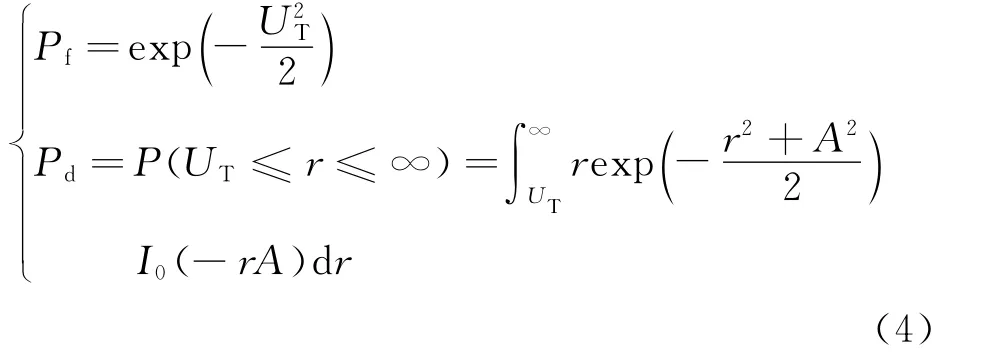
where UTis the detection threshold and I0（z）the zero－order modified Bessel Function.Variable A satisfies the following formula

where SNR is the ratio of signal to jamming and it can be calculated by［4］

where Ptis the radar transmit power；Gtthe radar antenna gain；σthe cross－sectional area of the target；Rtthe range from target to radar；Rjthe range from jammer to radar；Pjthe jammer transmit power；Gjthe jammer antenna gain；Vjthe polarization loss from jammer to radar antenna；and G′tthe antenna gain of radar antenna in the direction of the jammer.When the fighters ultilize a self－screening jamming，we get Rt＝Rjand G′t＝Gt，then

When the detection side builds a radar network composed of multiple dispersive radars，it uses rank－K fusion rule for decision－making.Then，the overall detection probability PDKnand the overall false alarm probability PFKnof the network can be calculated as follows［27］

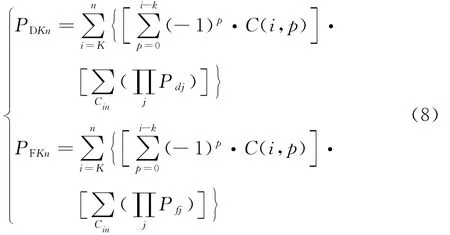
According Eqs.（2－8），PDKncan be abstracted as a function of the decision variables of both sides.Thus，in the game model，we select PDKnas the benefit of jamming side and－PDKnas the profit of detecting side，i.e.，

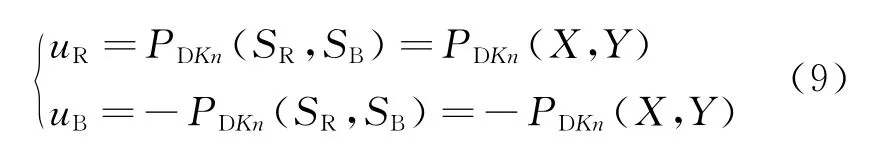
During the decision process，the jamming side expects a detection probability as low as possible with a choice of（X，Y）and contrarily the detecting side wants the highest probability.Then，the game－based decision model can be formulated as

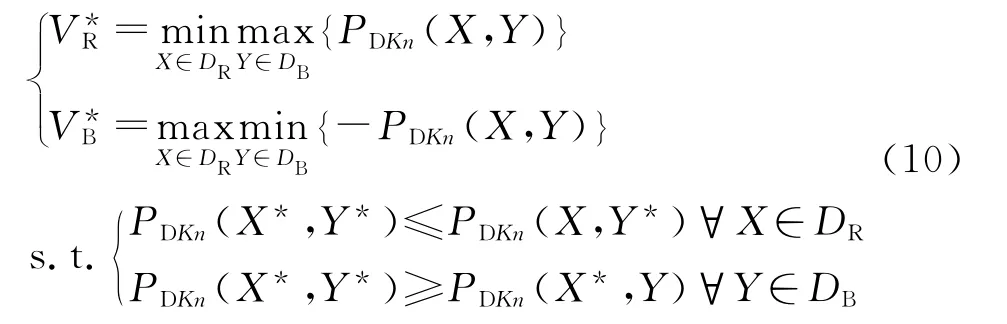
where V＊Rand V＊Bare the optimal game values of red and blue sides，respectively and（X＊，Y＊）is the final Nash Equilibrium strategy of the game model.

2.2 Problem solving

The game－based collaborative power allocation model seeks the most appropriate powers for both sides according to the situations and strategy of the opponent.Since there exists huge decision space when the combat unit increases，it will be much more difficult to reach the game equilibri－um.To improve the efficiency，we present a stage－hierarchical method to turn a complex multidimensional game［28］into numerous simple onedimensional games，thus simplifying the optimization process.

In Fig.2，after decomposing，the first round gaming centralizes on the red side.It works out the jamming power allotted to each fighter for jamming the nradars，as well as the total detection powers of nradars for detecting each fighter.Then，the decision variables of the first round gaming are denoted as

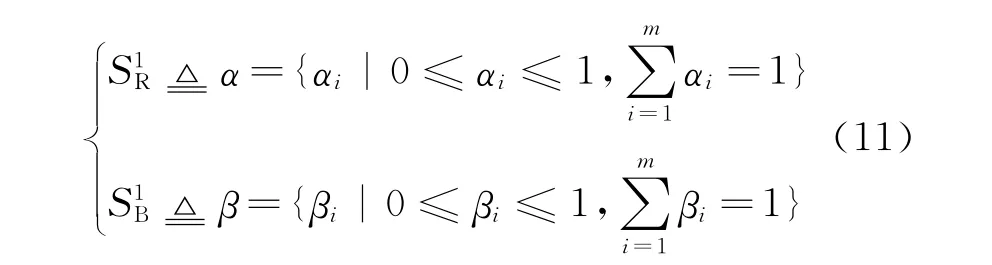
whereαiandβiare the decision variables of both sides of the first round gaming.They indicate that the ith fighter of red side gets a jamming power ofαi·PJallwhile the blue side allocates a detection power ofβi·PTallfor detecting the ith fighter.

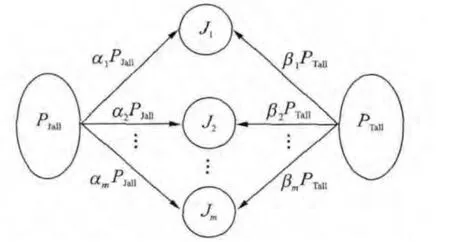
Fig.2 Situation of the first round gaming

Following the first round gaming，the original complicated game model is broken into monedimensional models，whose game situations are 1 versus n.That is to say，the ith（i＝1，…，m）fighter of the red side with a total jamming power ofαi·PJallwill counter against all the nradars of the blue side with a total detection power ofβi·.

The second round gaming centralizes on the blue side which figures out the jamming power that the ith（i＝1，…，m）fighter emits to the jth（j＝1，…，n）radar and the detection power that the jth（j＝1，…，n）radar emits to the ith（i＝1，…，m）fighter.As shown in Fig.3，the decision variables of the second round gaming are denoted as

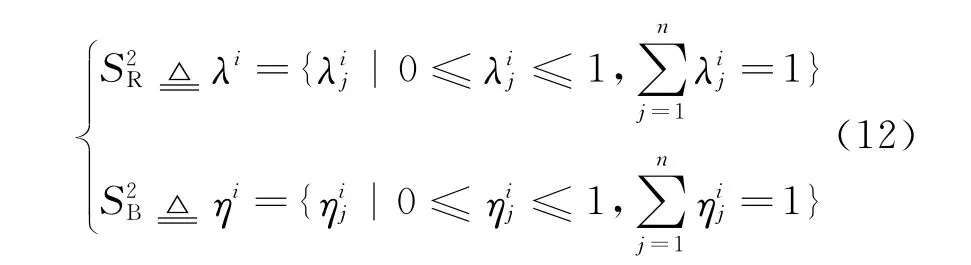
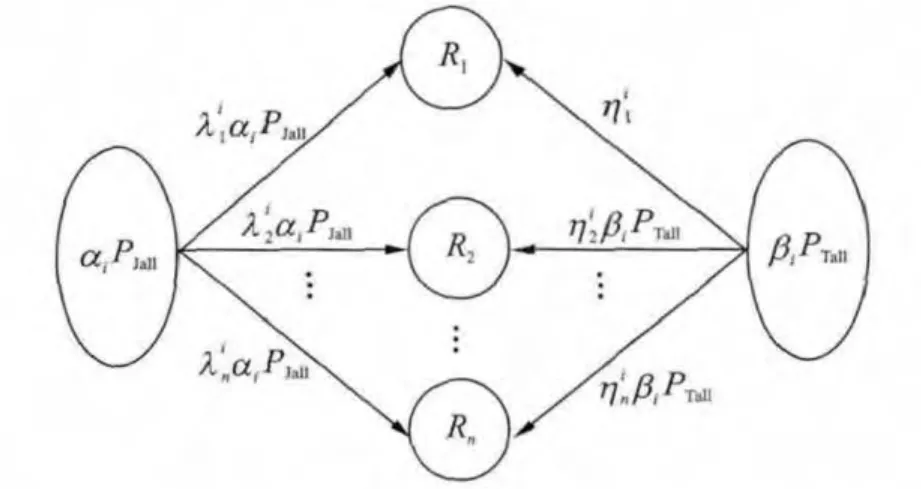
Fig.3 Situation of the second round gaming

The stage－hierarchical method described above can simplify the problem solving process and improve the problem solving efficiency deeply.The one－dimensional continuous game models can be solved following the method introduced in Ref.［29］，where the continuous model is discretized to obtain an infinite approximation of the two－person zero－sum game.Then，the optimal mixed strategy will be achieved as

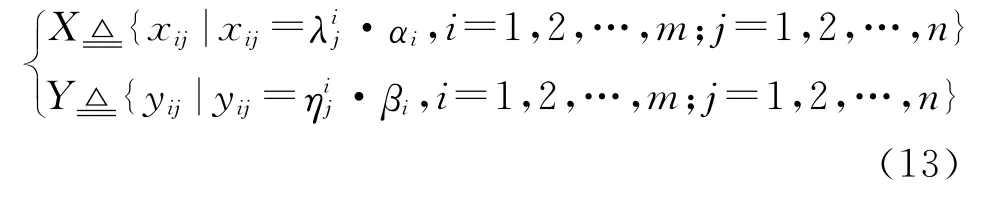
3 Results and Discussion

A scenario of two fighters versus two radars is analyzed here.As an offence side，the red formation consists of two fighters whose ECMs work at a self－screening jamming mode.In addition，the blue side is composed of two ground defense radars which have already been combined into a detecting network.To decrease the detection probability，the red fighters collaboratively manage the jamming power according to the relative situation and possible strategies that the blue side may choose.Meanwhile，the blue radars also manage their power to obtain a higher detection probability.Then，agaming begins between the red and blue sides.

Set the simulation parameters as follows：PJall＝800W，Gj1＝Gj2＝10db，σ1＝σ2＝10m2，Vj1＝Vj2＝0.5；PTall＝2 000kW，Gt1＝Gt2＝80db.The rank fusion rule of the detecting probability of the radar network is set as K＝2.All the radars have the same constant false alarm probability（CFAR）of Pf＝1.0e－6.With the above parameters，aproblem in the typical situation is solved and discussed in the following.

Assuming a typical situation as shown in Fig.4，we obtain the numerical expression in Table 1by quantifying the positions in the coordination of North－Sky－East.

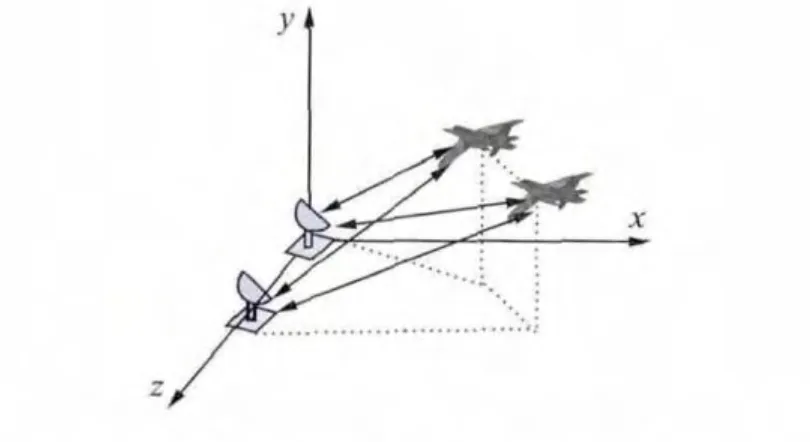
Fig.4 Situation of offense and defense

Table 1 Quantified situation

3.1 The first round gaming

According to the hierarchical method described in Section 3，the first round gaming decides how to allocate the 800Wjamming power to J1，J2for jamming the blue radars，and how to divide the 2 000kW detection power into two pieces which are used to detect J1，J2，separately.To solve this high level gaming model，we carry out a discretization of N＝10and figure out the mixed Nash equilibrium（MNE）with the help of lingo programming toolkit（LPT）.The results of the first round gaming are shown in Table 2.

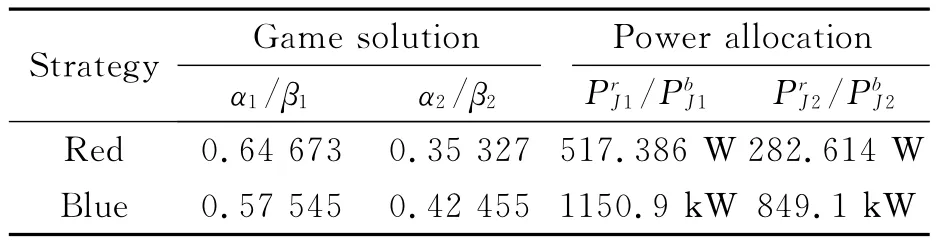
Table 2 Results of the first round gaming

3.2 The second round gaming

The second round gaming consists of two one－dimensional games.As one of them，the game J1versus R1，R2works out the optimum strategy of how to divide the jamming powerinto two pieces for jamming R1，R2and how to allocate the detection powerto R1，R2for detecting J1.Similarly，the game J2versus R1，R2is used to decide how to divide the jamming powerinto two pieces for jamming R1，R2and how to allocate the detection powerto R1，R2for detecting J2.The results of the second round gaming are shown in Tables 3，4.

Table 3 Results of the gaming J1versus R1，R2

Table 4 Results of the gaming J2versus R1，R2

3.3 Discussion of the results

Synthesizing the two round gaming results，the final results are shown in Table 5.

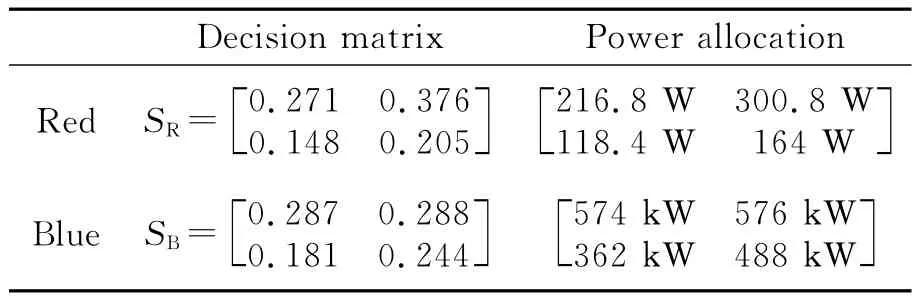
Table 5 Results of final strategy

Corresponding with the equilibrium strategy in Table 5，we define marginal strategy as SM＝andequipotentstrategyasS＝ETo verify the optimality of the equilibrium strategy，a series of comparative trials have been conducted.

Table 6shows the comparative trials of typical strategies and Fig.5compares the detecting probabilities of all the trials.

Table 6 Comparative trials of typical strategies

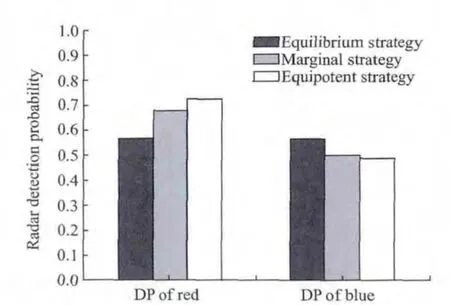
Fig.5 Bar chart of comparative trial results

In Fig.5，compared with equilibrium strategy，both the marginal strategy and equipotent strategy will produce a higher detection probability for the red side，which means that it will be more easily detected by the blue radars when the red side adopts the marginal strategy or equipotent strategy.Accordingly，the blue side will get a worse detection performance when the marginal strategy or equipotent strategy is adopted.In fact，any strategy that differs from the equilibrium strategy can reach the same conclusion.Only the equilibrium strategy

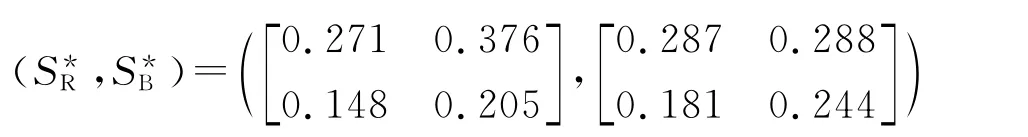
can meet the limits of

Therefore，the equilibrium strategy shown in Table 5is optimal in the strategy set of the con－structed game model.

The comparison between allocating results of the red side′s jamming power is shown in Fig.6.It shows that both J1and J2allocate more jamming power to R2rather than R1.The reason is that R2is closer to J1，J2than R1in the situation（as shown in Table 1）and R2radiates more detection power to J1，J2than R1（as shown in Fig.7），which indicates that the red side is apt to emit more jamming power to the radar with a bigger situational threat or energy threat.Similarly，the optimal strategy of the blue side makes R1，R2emit more detection power to the fighter with a higher degree of situation threat or energy threat，as shown in Figs.6，7.According to the above discussion，the game model can provide more practical approximation of the actual military conflict，and certainly it will provide a more reasonable decision.

Fig.6 Power allocation contrast of red side

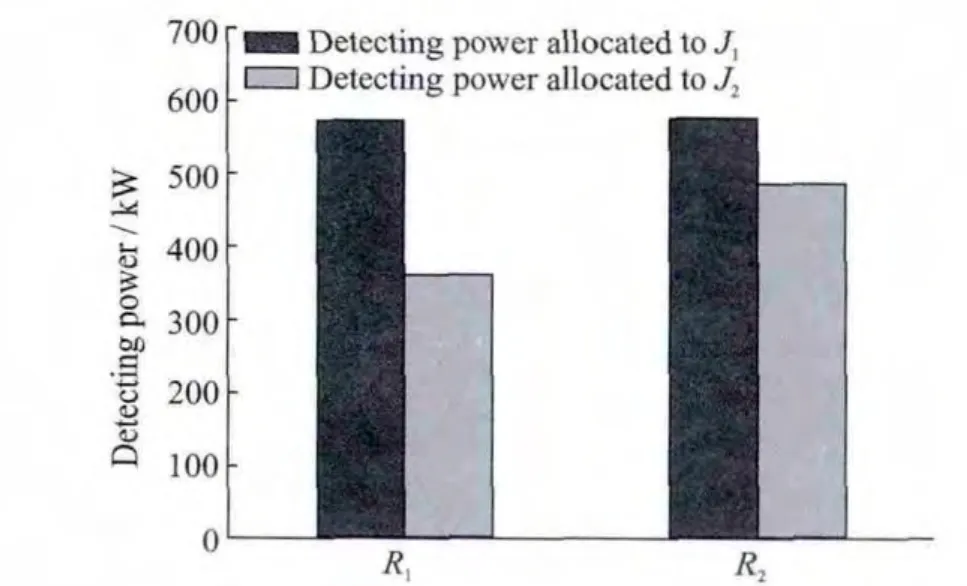
Fig.7 Power allocation contrast of blue side

4 Conclusions

The collaborative management of power resources for offence－defense counterwork between radar and jamming is addressed.A two－person general－sum continuous－game－based model is built for dynamic allocation of the power resources.With consideration of the situation and strategies the opposing side may take，the optimum solution can be more practical.To simplify the solving process，on the basis of a discussion about the model complexity，we work out a hierarchical processing method to promote computational efficiency by breaking the complicated model into numerous small one－dimensional games.With a contrastive analysis of the simulation results，we draw a conclusion that the equilibrium strategy of the game model can realize the optimal allocation of the power resources.When using the equilibrium strategy，more power will be allocated to the target that produces a higher degree of situational threat or energy threat，which means that the gamed－based model and the equilibrium strategy can provide a reasonable decision.

［1］ Li Bo，Gao Xiaoguang.Algorithm of power allocation for cooperative electronic jamming in air combat of formation［J］.Systems Engineering and Electronics，2008，30（7）：1298－1230.（in Chinese）

［2］ Wang Hongjun，Chi Zhongxian.The research on fleet jamming plan decision－making based on collaboration［J］.System Engineering Theory and Practice，2007，（4）：171－175.（in Chinese）

［3］ Xu Zhenhai，Wang Xuesong.Optimum allocation of barrage jamming power in netted radar countermeasure［J］.Systems Engineering and Electronics，2003，25（6）：655－657.（in Chinese）

［4］ Wan Kaifang，Gao Xiaoguang，Liu Yu.Optimal power partitioning for cooperative electronic jamming based on Lanchester with variable efficiency factors［J］.Systems Engineering and Electronics，2011，33（7）：63－67.（in Chinese）

［5］ Pham K D.Cooperative decision problems with confrontation of jamming and estimation：Multi－resolution strategies for performance robustness［C］／／Proc of 16th Mediterranean Conference on Control and Automation.Ajaccio，France：［s.n.］，2008：982－989.

［6］ Wu Y L，Wang B B，Ray K J.Optimal power allocation strategy against jamming attacks using the colonel blotto game［C］／／Proc of IEEE“GLOBECOM”.［S.l.］：IEEE Communications Society，2009.

［7］ Schrage D，Farnham C.A market－based optimization approach to sensor and resource［J］.Intelligent Computing：Theory and Applications，2006，6229：62290I1－62290I9.

［8］ Yang Shaohuan，Gao Xiaoguang，Fu Xiaowei.Search path planning of unmanned aerial vehicles based on game theory［J］.Systems Engineering and Electronics，2011，33（10）：2254－2257.（in Chinese）

［9］ Hou Dingpi.The introduction of game theory［M］.Anhui，China：Press of National Science and Technology University，2004.（in Chinese）

［10］He Jianhua，Gao Xiaoguang.An algorithm based on game theory for exploring how to obtain NCW information superiority in 1vs1air combat［J］.Journal of Northwestern Polytechnical University，2008，26（2）：142－145.（in Chinese）

［11］Liu J G，Zhang X F，Wang N S.Manufacturing system scheduling based on multi－agent cooperation game［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2007，24（4）：329－334.

［12］Zhu Hai，Zhang Bing.Multi－sensor resource distribution based on inequality game theory［J］.Electronics Optics and Control，2008，15（6）：18－21.（in Chinese）

［13］Wei M，Chen G S，Pham K.Game theoretic target assignment approach in ballistic missile［J］.Signal and Data Processing of Small Targets，2008，6969：69690N1－69690N9.

［14］Sang B H，Jiang C S.Virtual target differential game midcourse guidance law for hypersonic cruise missile based on neural network［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2008，25（2）：121－127.

［15］Song T L，Musicki D.Target existence based resource allocation［J］.IEEE Transactions on Signal Processing，2010，58（9）：4496－4506.

［16］Tang Z L.Multi－objective shape design in aerodynamics using game strategy［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2005，22（3）：195－199.

［17］Song C Z，Zhao Y Q，Xie N G.Multiobjective optimization of eight－DOF vehicle suspension based on game theory［J］.Transactions of Nanjing University of Aeronautics and Astronautics，2010，27（2）：138－147.

［18］Yao Zongxin，Li Ming，Chen Zongji.Mission decision－making method of multi－aircraft cooperative attack multi－objectbased on game theory model［J］.Aeronautical Computing Technique，2007，37（3）：7－11.（in Chinese）

［19］Fu Chao，Yang Shanling.Multi－UAV cooperative fight simulation system based on game theory［J］.Journal of System Simulation，2009，21（9）：2591－2594.（in Chinese）

［20］Li Dengfeng，Sun Tao，Wang Yongchun.Differential game model and its solution for the firepower－assignment in vessel formations in information war［J］.Control Theory and Applications，2008，25（6）：1163－1166.（in Chinese）

［21］Wei M，Chen G S，Cruz J B.Game－theoretic modeling and control of military air operations with civilian players［C］／／Proc of Guidance，Navigation，and Control Conference and Exhibit.Keystone，Colorado：AIAA，2006.

［22］Robb M C，Tsoundos A，White B A.Earliest intercept line guidance using agame theory approach［C］／／Proc of Guidance，Navigation，and Control Conference and Exhibit.Keystone，Colorado：AIAA，2006.

［23］Wang Yuyan，Li Bangyi，Shen Liang.Analysis on price decision of closed－loop supply chain［J］.Journal of Najing University of Aeronautics and Astronautics，2008，40（2）：275－278.（in Chinese）

［24］Zhao Huiliang，Jiang Hongli，Li Shouwei.Supervision of medical equipment industry based on evolutionary game［J］.Journal of Najing University of Aeronautics and Astronautics，2010，12（2）：25－28.（in Chinese）

［25］Jang J S，Tomlin C J.Control strategies in multiplayer pursuit and evasion Game［C］／／Proc of Guidance，Navigation，and Control Conference and Exhibit.San Francisco，California：AIAA，2005.

［26］Feng W J，Jiang W H，Wang R R.Joint resource allocation in cluster－based cognitive radio networks［C］／／Proc of International Conference on Communications and Mobile Computing.［S.l.］：IEEE Computer Socity，2010：179－182.

［27］Wang Guoyu.The digital simulation and evaluation of radar electronic warfare system［M］.Beijing，China：Press of National Defence Industry，2004.（in Chinese）

［28］Peng Y Y，Wang H P，Wang Zh P.Decision－making of aircraft optimum configuration utilizing multidimensional game theory［J］.Chinese Journal of Aeronautics，2010（23）：194－197.（in Chinese）

［29］Jiang Dianyu.The application of game theory with entropy［M］.Anhui，China：Press of Science Technology，2008.（in Chinese）