Temperature－Dependence of Microstructure Evolution in a Ferroelectric Single Crystal with Conducting Crack

Huang Cheng（黄成），Gao Cunfa（高存法）＊＊，Wang Jie（王杰）

1.State Key Laboratory of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics，Nanjing，210016，P.R.China；2.School of Aeronautics and Astronautics，Zhejiang University，Hangzhou，310058，P.R.China

1 Introduction

Ferroelectric ceramics have received much attention owing to their temperature－dependent spontaneous polarization which can be switched below its Curie temperature by applied electric or／and mechanical loading，making them have wide applications in temperature sensors，actuators，capacitors and transducers.However，the ferroelectric materials are intrinsically brittleness and prone to fracture［1］.Therefore，it is necessary to study fracture behavior of ferroelectric materials under applied electric and mechanical loads.Generally，insulating and conducting cracks are two main models simulating the fracture behavior of ferroelectric materials.Under such a high local electric field，air discharge may occur inside the crack，and consequently the crack is converted into a conducting one［2］.Thus，conducting cracks in ferroelectric materials have received great theoretical and practical interest in recent years.Mc－Meeking［3］solved the problem of an electric field around a conductive crack in di－electrics，which showed that an electric field caused stress intensification at the tip of a conducting crack.Suo［4］performed the failure behavior of conductive tubular channels in ferroelectric ceramics.Ru and Xiao［5］gave a systematic analysis of conducting cracks in a poled ferroelectric based on the stripsaturation model，showing that an electric field loading，applied parallel to the poling axis，would not induce any stress intensity factor at a conducting crack parallel or perpendicular to the poling axis.Zhang and Gao［6］introduced the strip dielectric breakdown（DB）model to study the failure behavior of ferroelectric ceramics.Zhang and Gao［7］used the DB model in fracture analysis of the electrostictive material with a conducting crack.Their results showed that the electric field loading parallel to the crack would retard its propagation before the occurrence of DB.

It is well known that the above mentioned models are based on linear piezoelectricity or simplified electrostrictive theories，which can show linear piezoelectric response at low electric field.However，ferroelectric materials exhibit strong nonlinear response under a large mechanical and／or electrical loading.Such nonlinear effect becomes particularly significant near the crack tip due to the singularity and field concentration.Related studies are focused on the toughening of conducting cracks due to domain switching.In the previous research，polarization switching is based on switching criteria，which is proposed by Hwang et al［8］.Under small scale conditions，Beom and Youn［9］developed the domain switching model to deal with the effects of electric fields on fracture behavior for a conducting crack.Their results show that the crack tip stress intensity factor is negative at small value of the coercive electric field to the applied electric loading.

In recent years，phase－field or time－dependent Ginzburg－Landau（TDGL）models，describing the formation and evolution of individual ferroelectric domains around the cracks explicitly，have become an increasingly important approach in the study of nonlinear behavior of ferroelectric materials［10－14］.The major advantage of the phase field simulations is that the polarization switching is the result of the total free energy minimization of the simulated system，in which no pre－described switching criteria are given in advance.

Recently，Wu et al.［15］have exhibited the complex role of temperature and dislocations in the domain switching of ferroelectric single crystal by using phase field simulation.Amir and Arias［16］extended the simulation of the propagation of conducting crack under purely electrical loading.Their results showed oblique crack propagation and crack branching from the crack tip.Although phase field simulations have been employed to investigate the domain switching process around the conducting crack tip，it still lacks of the underlying mechanism of the temperature－dependent behavior of ferroelectrics.In this paper，the effect of a conducting crack on the temperature－dependent behavior is simulated based on TDGL models.

2 Simulation Methodology

Consider an isotropic ferroelectric single crystal，the static equilibrium equations in any arbitrary volume Vand its bounding surface Scan be expressed as

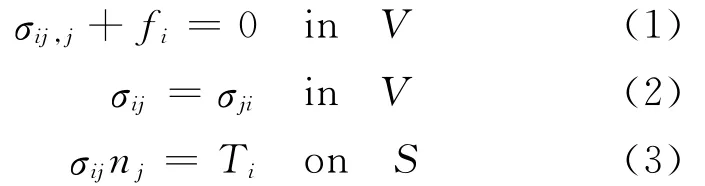
whereσijis the Cartesian components of the Cauchy stress，fithe mechanical body force，Tithe surface traction，and nithe unit vector normal to a surface element.

Under the assumptions of linear kinematics，the strainεijis linked to displacements uias

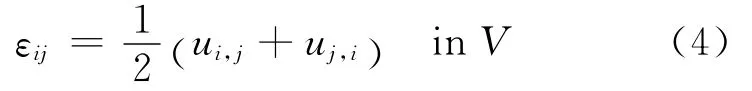
Meanwhile，the quasi－static forms of Maxwell’s equations in any arbitrary volume Vand its bounding surfaces Sare given by

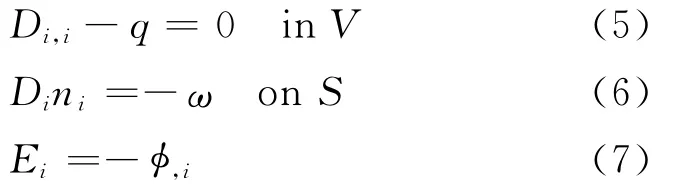
where Di，Ei，q，ω，andφare electric displacement，electric field intensity，volume charge density，surface charge density and electric potential，respectively.For the case of ferroelectrics，the paraelectric phase transforms into ferroelectric phase when the temperature is lower than its Curie point.In the present work，the spontaneous polarization Piis assumed to be embedded in a paraelectric background material.It is more suitable to employ the spontaneous polarization as the order parameter to calculate thermodynamic energies of the ferroelectric phase in our phase field models.Note that the electric displacement can be decomposed into two parts such that

whereκ0andare the permittivity of vacuum and total polarization，respectively.The total polarizationcan be divided into two components

whereκris the dielectric constant of the background material.Substituting Eqs.（9，10）into Eq.（8）yields

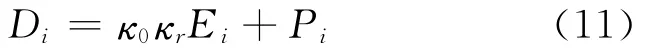
In this phase field approach，the temporal evolution of the polarization can be calculated from the following TDGL equation［13］

测试波形如图2所示。绿色波形为测试点在RPT左侧网段的波形，橙色波形为测试点在RPT右侧网段的波形，黑色圆圈(①)中的数据帧为主设备BA发送的进入RPT之前的0x350端口的主帧，黄色圆圈(②)中的数据帧为经过RPT处理之后的0x350端口的主帧，绿色圆圈(③)中的数据帧为从设备D3回复的0x350端口的从帧。正常情况下，在红色圆圈(④)位置，应该会出现经过RPT处理之后的0x350端口的从帧，而此时并没有出现。

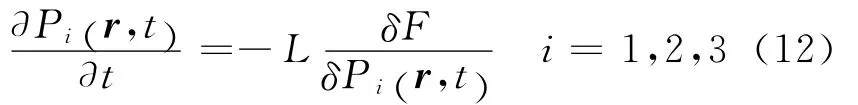
where t represents time，Lis the kinetic coefficient related to the domain mobility，δF／δPi（r，t）is the thermodynamic driving force for polarization evolutions，and rthe spatial vector，r＝ （x1，x2，x3）.To solve the TDGL equation，the total free energy Fcan be generally expressed as［13］

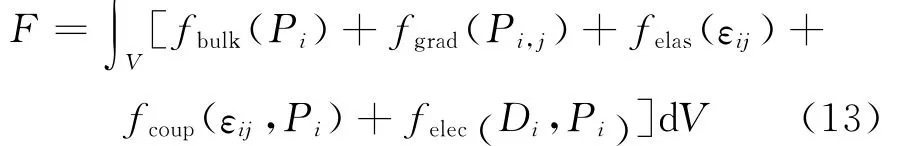
where fbulk，fgrad，felas，fcoup，and felecare the Landau free energy density，the domain wall energy density，the elastic energy density related to the total strain，the coupling energy density，and the electrostatic energy density，respectively.In phase field model，an equilibrium polarization vector field minimizes the total free energy of the system for fixed strain and electric displacement.For computational reasons，following a Legendre transformation，F＝＋DiEidV，the electrical enthalpy of ferroelectrics is a function of polarization Pi，polarization gradient Pi，j，strainεijand electric field Ei，which can be expressed as

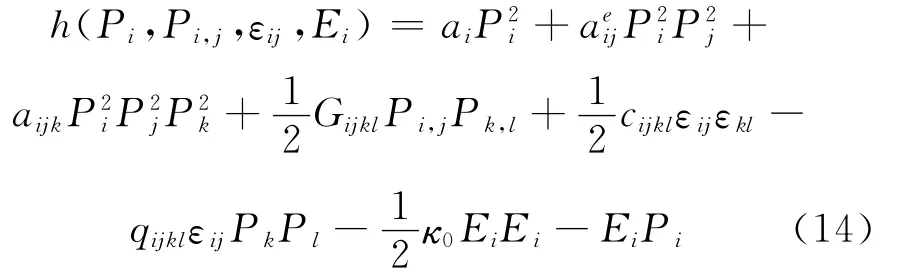
whereα1＝ （T－T0）／2κ0C0is the dielectric stiffness.αi，αeij，andαijkare the higher－order stiffness coefficients.T，T0，and C0are the temperature，Curie－Weiss temperature，and Curie constant，respectively.Gijklare the gradient coefficients，cijklthe elastic stiffness constants，and qijklthe electrostrictive coefficients.

Using the electrical enthalpy through the Legendre transformation，the mechanical equilibrium equations Eq.（1），the electrical equilibrium equations Eq.（5），and the dynamic evolution equation Eq.（12）in the present phase field model have the following forms，respectively.

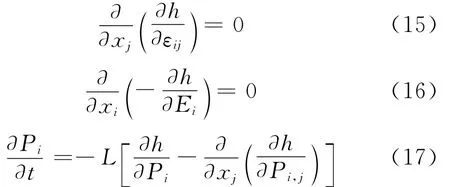
Here，the mechanical body force and extrinsic bulk charge are to be negligible.Using the variation of virtual work，a nonlinear multi－field coupling finite element method is employed［13］.The governing Eqs.（15－17）are expressed in the weak form as

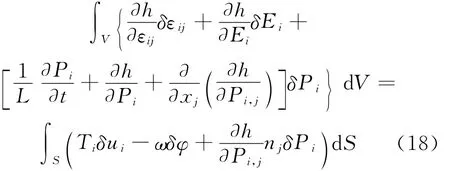
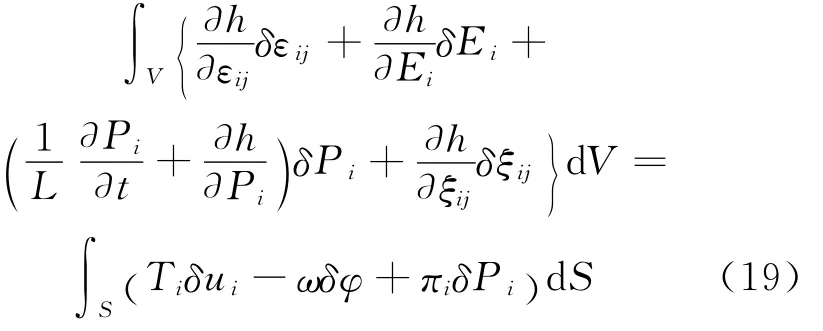
Eq.（19）is the foundation of the derivation of finite element equations for the model.For the space of discretization，authors employ an eightnode brick element with seven degrees of freedom containing three mechanical displacement，electrical potential and three spontaneous polarization components at each node.Finally the strain，stress，electric field，the electric displacement and polarization gradient are derived within the elements.The detailed formulation of the threedimensional（3D）finite element method can be found in our previous work［13］.

3 Simulation

3.1 Simulation model and its parameters

In order to perform numerical simulations，a 3DPbTiO3ferroelectric single crystal plate with a conducting crack in the center is simulated under the applied electrical and mechanical loadings in the present work.A schematic drawing of the ferroelectric single crystal with a conducting crack is shown in Fig.1.

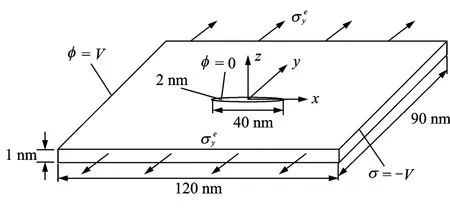
Fig.1 Schematic drawing of ferroelectric crystal

The dimension of simulated ferroelectric plate in the x，y，zdirections are 120，90，1nm，respectively.Here，the conducting crack is treated as a narrow but open ellipse.The sizes of semi－axis for the elliptical crack are 20nm and 1nm，respectively.To create a conducting crack，the electric potential is fixed to zero along the crack surface.The electric potentials on the left and right sides are set as－Vand V，respectively.Therefore，different electric loadings can be applied in the xdirection by giving different values for driving voltage V.The electric boundary conditions on other surfaces are set as zero surface charges（i.e.，Dini＝0）.On the upper and bottom surfaces，a uniform tensile stress is applied.The mechanical boundary conditions on the other surfaces are chosen to ensure the traction free condition.Here，free－polarization boundary conditions are commonly assumed，corresponding to zero gradient flux（i.e.＝0）.In the sim－ulation，3Dbrick elements are used.For computational reasons，the element thickness in the z direction equals the plate thickness，so the simulation can degenerate into the plane stress problem.Fig.2（a）shows the details of the mesh partition of the ferroelectric single domain.A refined mesh is generated in a small region of interest around the crack tip as shown in Fig.2（b），where the size is small enough relative to the width of domain walls.

The material parameters of PbTiO3are listed in Table 1［13］.In order to avoid divergence，authors employ the following set of dimensionless variables in the simulations.

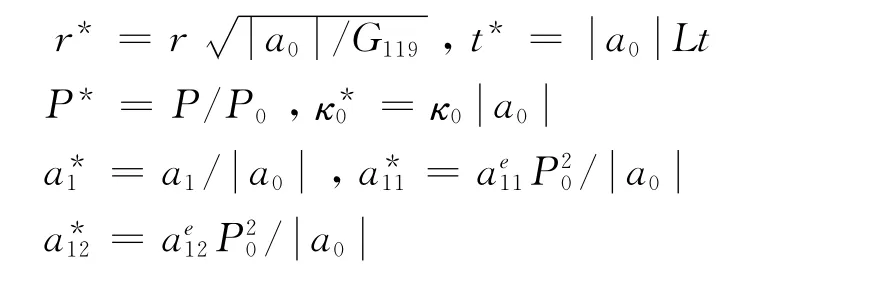
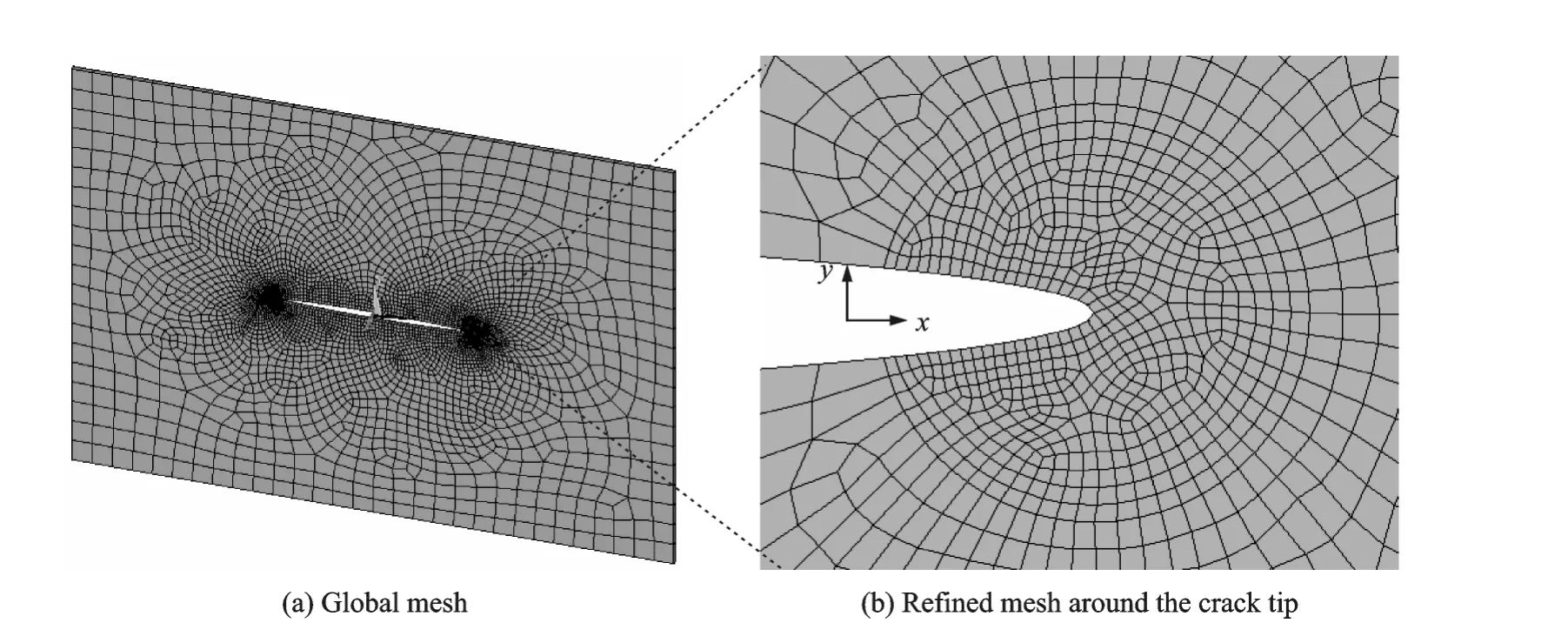
Fig.2 Mesh partitions of simulated ferroelectric single crystal with a conduction crack

Table 1 Values of material coefficients for PbTiO3used insimulations

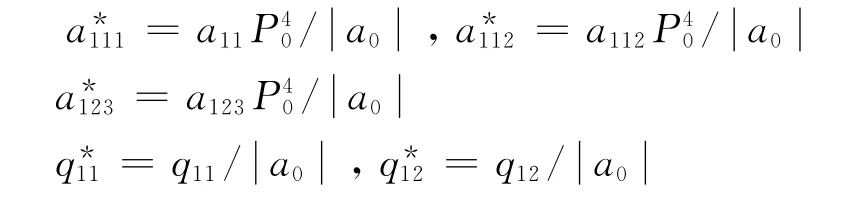
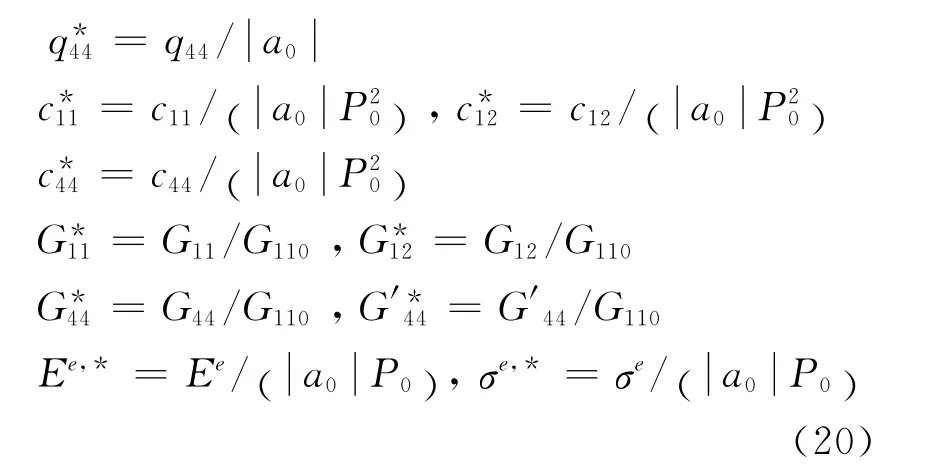
The normalized material coefficients are listed in Table 2.

Table 2 Values for the normalized coefficients in simulations

3.2 Simulation results and discussion

Figs.3shows the effects of the applied electrical loading on the microstructure evolution，electric field and stress field distribution ahead of the conducting crack tip under the room temperature.

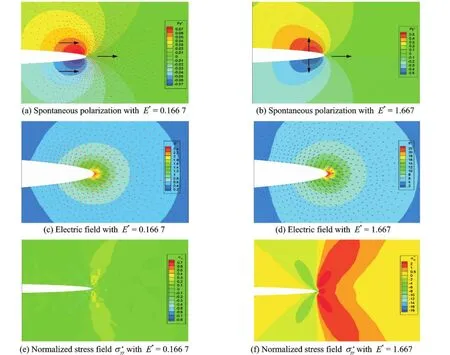
Fig.3 Effects of the applied electrical loading on ferroelectric domain structures at room temperature

Figs.3（a，c，e）correspond to the distributions of spontaneous polarization，the electric field and the normalized stress fieldσ＊yyahead of the conducting crack with E＊＝0.166 7，respectively.Figs.3（b，d，f）show the same physical quantities as Figs.3（a，c，e）with E＊＝1.667，respectively.The arrows in all the figures denote the direction of the spontaneous polarization.From Fig.3，it is found that the region beside the crack tip forms a nearly 90°angle to the poling direction in a small scale.The shape of the switched zone is almost symmetrical with respect to the crack，but the switching direction is asymmetrical.Therefore，the applied electric field induces the charge accumulation ahead of the crack tip，which in turn causes a high electric field around the crack tip.The intensified electric field contains huge electrostatic energy，and further brings forth the domain switch of 90°.Since domain switch near the crack tip reduces the poten－tial energy of the system，the microstructure evolution finally generates an internal stress field，resulting in switch－toughening，as shown in Figs.3（e，f）.Figs.3（e，f）show that the normalized stress fieldσ＊yyahead of the crack tip is found to be positive at the right side，but it lowers the stress at the left side.From Fig.3，it is found that the positive electric field tends to keep the stress intensity factors negative.Nevertheless，the increasing electric field leads to high local electric field ahead of the crack tip，which will enhance the electric field intensity factor.The result is consistent with many previous theoretical works and experimental observations［1］.

To investigate the mechanism on the temperature－induced switching behavior in a single crystal，the temperature－dependence of the spontaneous polarization and stress field near the crack tip with E＊＝1.667is shown in Fig.4.

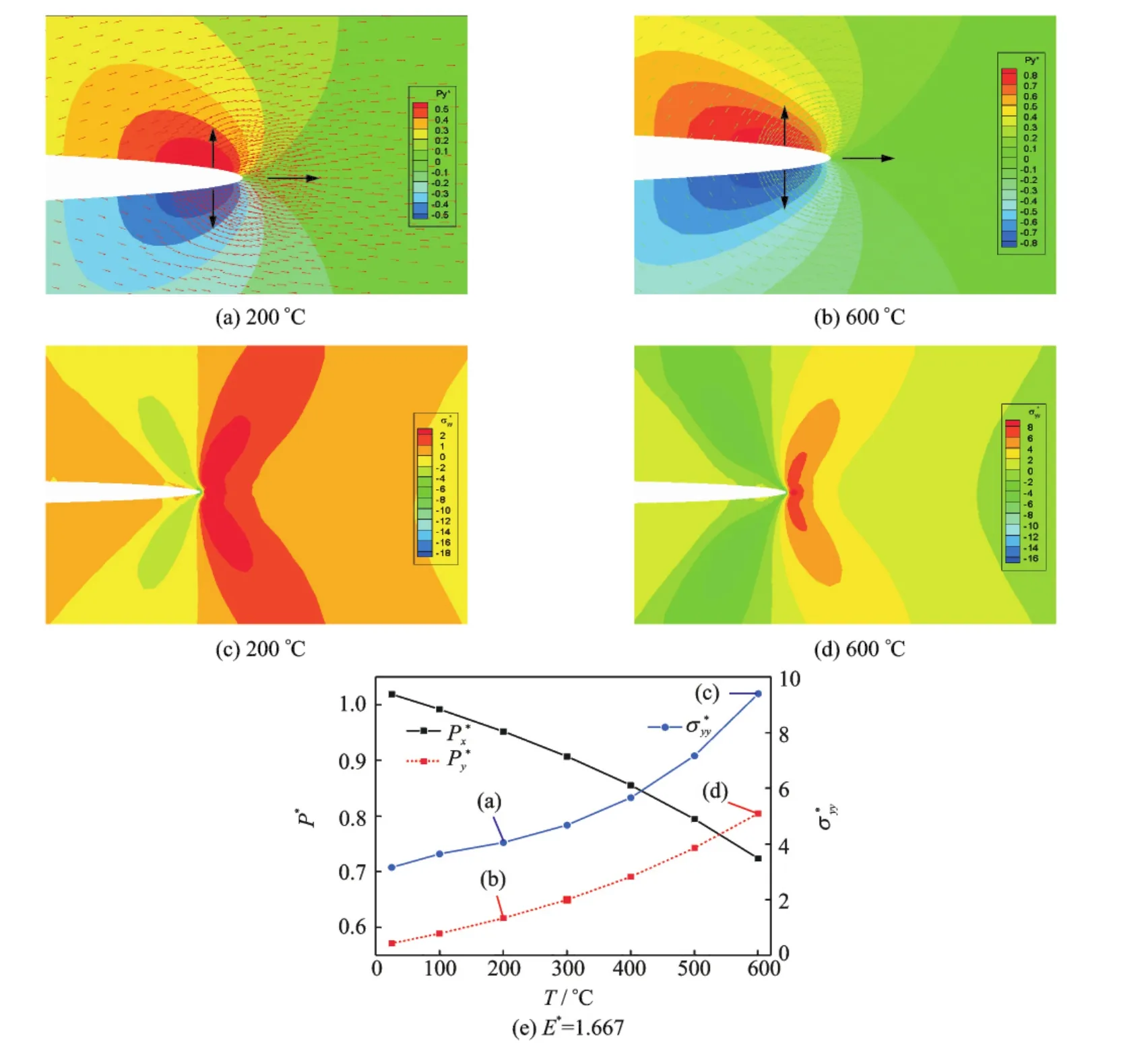
Fig.4 Temperature dependence of spontaneous polarization and stress field near crack tip with E＊ ＝1.667

From Fig.4，it is found that with the temperature increasing，the spontaneous polarization increases along the ydirection while decreases along the x direction.The temperature－induced microstructure evolution，expanding the typical 90°domain switching region along the conducting crack surface，in turn，causes the stress fieldσ＊yyto increas.It is indicated that increasing the temperature will enhance the crack propagation with E＊＝1.667，resulting in switch－weakening.

Furthermore，the effects of applied E＊＝1.667andσe，＊yy＝20on the temperature－dependence of the spontaneous polarization and stress field near the crack tip are shown in Fig.5.

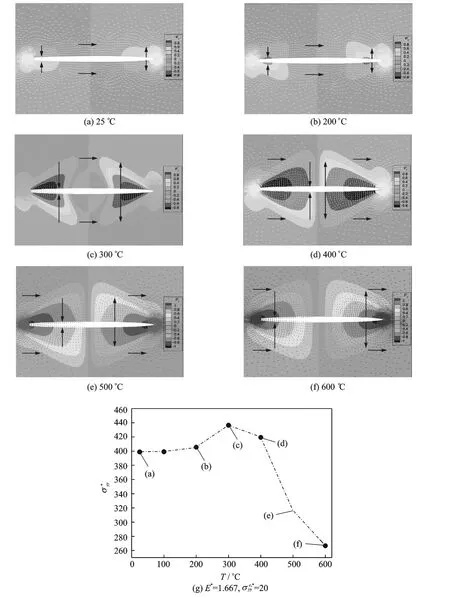
Fig.5 Temperature dependence of spontaneous polarization and stress field near crack tip with E＊＝1.667andσe，＊yy＝20

Figs.5（a－f）show the domain switching for a ferroelectric single crystal with a conducting crack at temperature from 25°C to 600°C.It should be mentioned that the stress fieldσ＊yyahead of the crack tip increases significantly when the combined tensile stressσe，＊yyand electric field load－ing are applied.The spontaneous polarization distribution of Fig.5（a）is similar to the saturation state in Fig.3（b），only the size of the 90°domain switching region becomes a little larger.From Figs.5（a－c），it is found that the spontaneous polarization component P＊yincreases when the temperature increases from 25°C to 300°C.It can be found that the switched zone moves backwards from the crack direction.Furthermore，the switched zones growing in both xand ydirections cause the increase of stress fieldσ＊yyin turn.There is a peak in the curve at T＝300°C，where it obtains the maximum stress fieldσ＊yy.It is implied that the total free energy of the system accumulates to a energy barrier.Therefore，the two switched zones grow to reduce total free energy，and the stress fieldσ＊yydecreases enormously with the temperature increase from 300°C to 600°C.The reduction of the stress fieldσ＊yymeans that the increase of temperature from 300°C to 600°C will impede the crack propagation with E＊＝1.667andσe，＊yy＝20，thus resulting in switch－toughening.

4 Conclusions

The temperature－dependence of the domain switching and nonlinear of a conducting crack in ferroelectric ceramics under the integrated electrical and mechanical loadings has been investigated based on a phase field approach containing the time－dependent Ginzburg－Landau equation.The effects of the applied electric field or／and mechanical loading on the microstructure evolution，electric field and stress field distribution ahead of the conducting crack tip are studied at the increasing temperature.A phase field simulation shows that increasing temperature will enhance the crack propagation with the purely high electric field of E＊＝1.667，which results in switch－weakening.Especially the increase of temperature from 300°C to 600°C will impede the crack propagation with E＊＝1.667，andσe，＊yy＝20，thus resulting in switch－toughening.

In summary，phase field simulations of ferro－electric materials are capable of exhibting detailed microstructure to investigate the mechanism on the temperature－induced switching behavior in a single crystal by applying combined tensile stress and electric field loading.Therefore，aphase field model of ferroelectric ceramic can simulate or／and predict the fracture behaviors in a conducting crack under applied mechanical or／and electric field loading at unusual temperature.

Acknowledgements

We thank the support from the National Natural Science Foundation of China（11232007）.Thanks also go to Prof.Zhang Tongyi for helpful discussions to improve the present work.

［1］ Kuna M.Fracture mechanics of piezoelectric materials—Where are we right now？［J］.Eng Fract Mech，2010，77：309－326.

［2］ Zhang T Y，Liu G N，Wang T H，et al.Application of the concepts of fracture mechanics to the failure of conductive cracks in piezoelectric ceramics［J］.Eng Fract Mech，2007，74：1160－1173.

［3］ McMeeking R M.On mechanical stresses at cracks in dielectrics with application to dielectric breakdown［J］.J Appl Phys，1987，62：3119－3122.

［4］ Suo Z.Models for breakdown－resistant dielectric and ferroelectric ceramics［J］.J Mech Phys Solids，1993，41：1155－1176.

［5］ Ru C Q，Mao X.Conducting cracks in a piezoelectric ceramic of limited electrical polarization［J］.J Mech Phys Solids，1999，47：2125－2146.

［6］ Zhang T Y，Gao C F.Fracture behaviors of piezoelectric materials［J］.Theor Appl Fract Mech，2004，41：339－379.

［7］ Zhang N，Gao C F.Effects of electrical breakdown on a conducting crack or electrode in electrostrictive solids［J］.European Journal of Mechanics A／Solids，2012，32：62－68.

［8］ Hwang S C，Lynch C S，McMeeking R M.Ferroelectric／ferroelastic interactions and a polarization switching model［J］.Acta Metall Mater，1995，43：2073－2084.

［9］ Beom H K，Youn S K.Electrical fracture toughness for a conducting crack in ferroelectric ceramics［J］.Int J Solids Struct，2004，41：145－157.

［10］Song Y C，Soh A K，Ni Y.Phase field simulation of crack tip domain switching in ferroelectrics［J］.J Phys D Appl Phys，2007，40：1175－1182.

［11］Su Y，Landis Chad M.Continuum thermodynamics of ferroelectric domain evolution：Theory，finite element implementation，and application to domain wall pinning［J］.J Mech Phys Solids，2007，55：280－305.

［12］Xu B X，Schrade D，Gross D，et al.Phase field simulation of domain structures in cracked ferroelectrics［J］.Int J Fract，2010，165：163－173.

［13］Wang J，Kamlah M.Three－dimensional finite element modeling of polarization switching in a ferroelectric single domain with an impermeable notch［J］.Smart Mater Struct，2009，18：104008.

［14］Gu H L，Wang J.The influence of crack face electrical boundary conditions on the nonlinear behavior of ferroelectric single crystal［J］.Smart Mater Struct，2013，22：065001.

［15］Wu H H，Wang J，Cao S G，et al.The unusual temperature dependence of the switching behavior in a ferroelectric single crystal with dislocations［J］.Smart Mater Struct，2014，23：025004.

［16］Abdollahi A，Arias I.Conducting crack propagation driven by electric fields in ferroelectric ceramics［J］.Acta Materialia，2013，61：7087－7097.