基于指数平滑方法的丝杠轴承故障时间预测

王强军

(中航工业成都飞机工业(集团)有限责任公司数控加工厂，四川 成都 610091)

数控机床作为现代生产系统中不可或缺的加工设备，其设备状态的完好与否直接决定着整个生产线能否正常运行［1］。然而，由于多种原因如产品设计、制造、装配缺陷、用户操作不当等导致机床在使用过程中频繁发生故障［2］，这给机床用户带来了巨大的经济损失，同时也对机床生产企业的声誉造成恶劣的影响。

在实际生产中，机床用户为了减少机床故障停机带来的巨大损失，为机床准备了大量的备品备件［3］，一旦机床发生故障，则立即对相应的元件进行更换。但是，这种防备的措施在实施过程中遇到了以下几方面的问题:首先，备品备件的种类，即需要预备什么元件;其次，备品备件的数量。为了解决困惑机床用户企业的这一难题，本文提出一种基于指数平滑方法的机床丝杠轴承故障时间的预测方法。首先，通过建立机床丝杠轴承故障时间的指数平滑模型，预测出该部件发生下一次故障的时间;其次，借助于系统可靠性经验建模方法，建立系统故障发生时间的概率分布函数或累计分布函数，并由此计算出发生下一次故障预测时间的概率;最后，以某机床丝杠轴承为实例，进行了分析。通过分析表明该方法能够较准确地预测机床丝杠轴承发生的时间，为机床备品备件策略及预防维修等活动提供了决策依据。

1 指数平滑模型的建立

1.1 指数平滑方法

指数平滑方法是时间序列预测方法之一，是在加权移动平均法的基础上发展起来的一种有效的预测方法［4］。时间序列的特点是数据资料先后顺序不能随意改动，主次的观测值通常不是独立的，分析时必须考虑观测值顺序。通过时间序列分析找出系统内在的统计和发展规律，并运用时间序列模型预测和控制未来［5］。指数平滑方法按平滑的次数可分为一次指数平滑法、二次指数平滑法、三次指数平滑法等。由于故障间隔时间序列通常无明显变化趋势，本文选取一次指数平滑方法。

1.2 故障时间一次平滑模型建立

设机床丝杠轴承故障间隔时间序列的观测值为yk，(k=1，2，…，T)，若记第k 期的简单算术移动平均值为

则k+1 期的预测值约定为

因而得到一递推公式

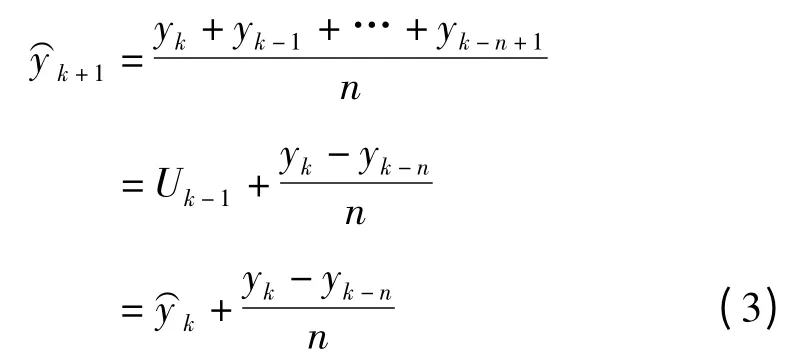
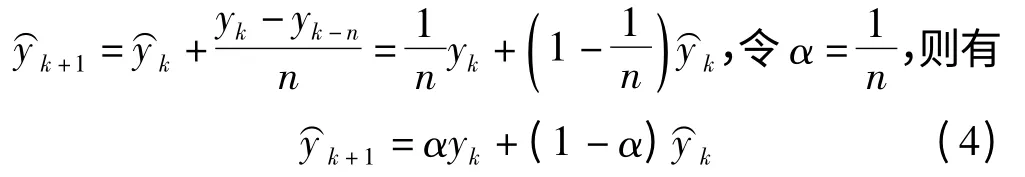
此为一次指数平滑的基本方程，这里1 ＜α ＜1 称为平滑常数。进一步，式(4)可变化为+α，此式表明，k +1 期的预测值等于第k期的预测值加上第k 期的预测误差的α倍。如果第k 期的预测值过低，则误差值＞0，第k+1 期的预测值增大;反之，亦然。可见，该方法有一定的自修正过程，能通过现在的预测误差自动修正下一期的预测值，通常α 体现修正的幅度。

设时间序列的观测值为y0，y1，…，yn，则由递推公式可得到

由此可看出，第k+1 期的预测值实质上是初始值和各时间点观测值的加权平均。式(5)中:

1.3 平滑常数及初值的选取

用一次指数平滑进行预测时，需要解决两个关键问题:

(1)初始预测值的选取

对于初始值的选取，可依据时间序列数据的多少而定，当数据较多时，初始值对预测值的影响可以忽略;而对于数据较少的时间序列，为减小预测误差，一般选用前期的观测值的平均值作为初始预测值;对于同一批产品或者设备，可取平均故障间隔时间的观测值作为初始预测值。

(2)平滑常数的选取

对于数控机床而言，由于故障之间的影响关系较为复杂，很难判断平滑常数α 的取值大小。事实上，当α 取值变化时，各时间点的预测值会呈现一定的波动，因而会使预测误差产生波动。预测误差大小常用平均绝对误差和均方标准差进行衡量。

为使预测值更为精确，本文以均方标准差最小为约束，选取平滑常数。采用迭代法求解最优平滑常数，α∈(0，1)从0 开始，步长设定为0.001，选取使均方标准差最小的平滑常数，并建立预测模型。

2 故障发生时间的概率分布函数

若将机床丝杠轴承部件故障发生时间看成是随机事件，则故障发生时间的统计模型能够描述该部件故障发生时间的分布情况，及故障发生的概率。假定机床丝杠轴承在T0时刻开始工作，Ti(i=1，2，…)表示系统第i 次故障的时间。给定一时刻T'，则可以得到一随机故障序列［6］:0=T0＜T1＜T2＜… ＜Tk≤T'，若用yk表示该部件第k 次和第k -1 次故障间隔时间，则有:yk=Tk-Tk-1。借助于可修复系统可靠性建模方法的基本思想，建立故障发生时间的概率分布函数。

2.1 模型初选

常用的经验分布模型如威布尔分布、对数正态分布、伽马分布、指数分布等均可作为经验分布函数。此处可参照参考文献［7］选择最佳分布模型。本文以威布尔分布为例进行实例分析。威布尔分布的概率密度函数如下:

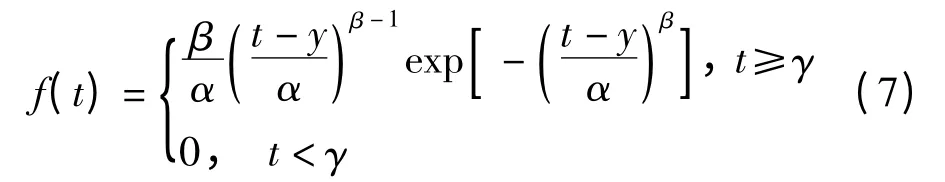
式中:α 为尺度参数，β 为形状参数，γ 为位置参数。

假定系统在初始时刻即发生故障，此时三参数的威布尔分布可简化为二参数威布尔分布

分布函数为

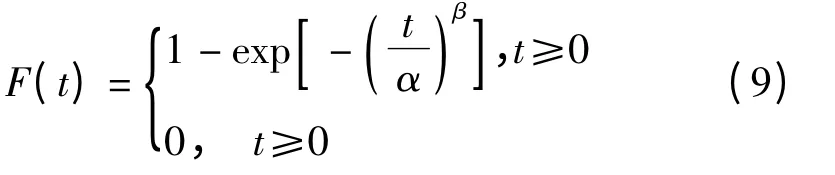
2.2 参数估计

模型参数估计常用的方法有最大似然函数法(MLM)和最小二乘法(LSM)，最小二乘法计算较为快捷，本文选择最小二乘法进行参数估计。

2.3 模型拟合优度检验

K-S 检验(又称D 检验［8］)和x2检验是两种常用的检验方法。但是K-S 检验主要适用于连续型变量，因此本文选取K-S 检验方法。

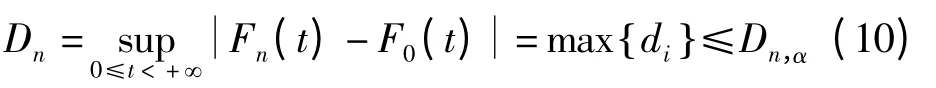
式中:F0(t)为假设分布函数;Fn(t)为经验分布函数。

式中:Dn，α为临界值;α 为置信水平;n 为故障数。

3 实例分析

3.1 故障时间预测

某机床丝杠轴承故障时间及相应的故障间隔时间如表1 所示。

表1 某机床丝杠轴承故障时间及间隔时间

按照均方标准差最小原则，建立平滑预测的模型为

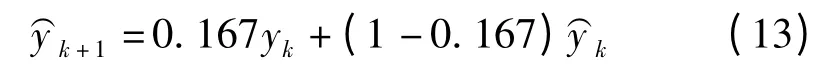
通过预测，该丝杠轴承X 发生下一次故障的间隔时间为

即该部件发生下一次故障的时间为2 455+111.057=2 566.057 h。

3.2 预测准确性评估

借助于经验建模方法，首先得到其故障时间的频率直方图如图1 所示。

从图1 可以看出，该批加工中心故障时间频率分布呈非对称单峰形式，故其故障时间分布模型不可能是指数分布，可能是威布尔或对数正态分布。由于威布尔分布尺度参数不断变化有较为广泛的拟合范围，本文选择两参数威布尔分布为初始模型。

对两参数威布尔分布函数

这样可通过最小二乘法进行求解。

最终建立其累计分布函数模型为

其函数曲线如图2 所示。

由前面预测结果，该部件发生下一次故障的时间为2 566.057h，则在该时刻，机床发生故障的概率为F(2566.057)=0.8699，即在2566.057 h，机床丝杠轴承发生故障的概率为0.869 9，预测的准确性能够达到86.99%。

4 结语

本文提出了一种预测机床丝杠轴承X 部件故障发生时间的预测方法，首先，建立了该部件故障间隔时间的一次指数平滑模型;其次，建立了该部件基于故障时间的概率分布模型，借助该分布模型，能够对一次指数平滑模型的准确度进行评估;最后，通过实例分析表明，该方法能够有效地对机床丝杠轴承部件的故障发生时间进行预测，且预测结果有较高的准确性，能够为该部件的备品备件及机床预防维修提供指导。

［1］Keller AZ，Kamth ARR，Perea UD.Reliability analysis of CNC machine tools［J］.Reliability Engineering，1982(3):449 -473.

［2］贾亚洲，于捷，姜巍巍，等.国产加工中心故障模式及影响分析［J］.江苏机械制造与自动化，2001(4):111 -114.

［3］鲍中美.预测技术在机床备件管理中的应用［J］.械制制造，2004，42(1)，58 -59.

［4］李时.预测与决策技术［M］.长春:吉林科学技术出版社，2008.

［5］刘罗曼.时间序列分析中指数平滑法的应用［J］.沈阳师范大学学报:自然科学版，2009，27(4):416 -418.

［6］郑锐，张英芝，申桂香，等.一种新的可修系统故障率模型［J］.吉林大学学报:工学版，2009，39(S2):324 -327.

［7］Wang Yiqiang，Jia Yazhou，Yu Junyi，et al.Fault probabilistic model of CNC lathes［J］.Reliability Engineering and System Safety，1999，65(3):307 -314.

［8］Kennedy Jr William J，Gentle James E.Statistical computing［M］.5th ed.New York:Marcel Dekker Inc Press，2005.