Spatial modeling of the carbon stock of forest trees in Heilongjiang Province, China

Chang Liu • Lianjun Zhang • Fengri Li • Xingji Jin

Introduction

The global carbon cycle is a natural process involving matter and energy, and occurring in the earth biosphere and atmosphere (Falkowski et al. 2000; Fang et al. 2001), in which land vegetation plays a key role (Granier et al. 2000; Law et al. 2001; Hazlett et al. 2005; Smith et al. 2006). In modern times, human activities caused increases in concentrations of atmospheric CO2, a greenhouse gas, from the burning of fossil fuels and this led to global warning. Development of technologies to control gas emissions to reduce the concentration of CO2has become a focal point for international research in many study areas (Houoatow 1997; Neilson et al. 2007). Forest ecosystems are considered the main carbon sinks in the earth biosphere. Carbon sequestration by forests is a process of absorbing, collecting and, storing CO2through photosynthesis (Kurz and Apps 1999; Heath and Smith 2000; Phillips et al. 2000; Sohngen and Mendelsohn 2003; Baral and Guha 2004). The carbon storage of a forest is usually considered to consist of several pools (Fahey et al. 2009). In this paper, forest carbon storage means carbon in the living trees, including stems, branches, foliage, and roots. To date, most research on forest carbon storage has been focused on forest biomass and carbon storage, but few studies have examined geo-spatial distribution of forest carbon storage, which is also an important factor affecting area-temperature, carbon emission, and the benefits of carbon sinks. For these reasons geo-spatial distribution of forest carbon storage has received increasing emphasis in recent years.

It is well known that the distribution of forest carbon storage is heterogeneous across geographical regions. Forest management regimes also have major impacts on forest carbon storage and intensity. It is crucial and necessary to obtain accurate and timely information on the changes of forest carbon storage within and between regions for management planning and policy making. However, traditional methods such as geostatistics, conventional regression, and Kriging, using readily accessible remote sensing data (Myeong et al. 2006), are inadequate to provide accurate estimation and prediction on the spatial distribution of forest carbon storage because of the low correlation between the reflective spectrum property of remote sensing and forest carbon stock (Sales et al. 2007; Du et al. 2010). More advanced spatial modeling methods have been developed and applied to improve and enhance the description and prediction of the spatial distributions of forest carbon storage, such as spatial lag model (SLM), spatial error model (SEM), spatially adaptive filtering model, and linear mixed model (LMM) (Anselin and Bera 1998; Zhang et al. 2009). These modeling techniques incorporate the spatial autocorrelations in the data into modeling processes to obtain better model parameters, and more importantly, unbiased estimation for the standard errors of model coefficients that improve statistical testing. These modelling methods have been applied in economics (Chi and Qian 2009), population studies (Chi 2010), forestry (Zhang et al. 2009; Lu and Zhang 2011) and other fields. Although capable of reducing spatial autocorrelation for residual, these models are global in scope and applicable to very large study areas. They are therefore less efficient at assessing spatial heterogeneity in forest carbon storage (Zhang and Gove 2005; Zhang et al. 2005; 2009).

Data on forest carbon storage are typically collected over large geographic regions. The differences between locations can be significant in terms of topographic features, species composition and richness, vegetation cover, and, consequently, forest biomass and carbon storage (i.e., spatial heterogeneity can be high). Each location is similar to adjacent neighboring areas, but dissimilar to distant areas. In recent years, localized summary statistics and modeling methods have been used to explore the effect of spatial heterogeneity in many studies (Pickett and Cadenasso 1995; Espa et al. 2013). In general, for any targeted location the descriptive statistics of response variables of interest are computed by weighting the neighboring locations within a user-defined bandwidth by a distance-decay function from the target location. The neighboring locations adjacent to the targeted location have more influence on the resulting descriptive statistics than do more distant locations. The localized descriptive statistics are therefore available for each location throughout the entire study area and this provides a direct way of assessing and visualizing the heterogeneity and scale dependence of ecological patterns across a geographic area (Brunsdon et al. 2002; Ma et al. 2011).

Geographically weighted regression (GWR) has become a popular approach to depicting spatial heterogeneity in a regression context (Brunsdon et al. 1996; Brunsdon et al. 1999; Fotheringham et al. 2001; Fotheringham et al. 2003; Charlton et al. 2009). GWR captures spatial variation by calibrating a regression model fitted at each location in the study area and weighting all neighboring locations by a distance-decay function from the targeted location. Thus, GWR provides a set of localized model parameters of the regression model at each location so that local spatial variation is fully incorporated into the modeling processes. With the rapid development of visualization tools of Geographic Information System (GIS), the model parameters, standard errors of the parameters, and model R2associated with each location can be mapped to illustrate spatial heterogeneity in the regression relationship under study. Consequently, the influence of micro-environment features, vegetation competition, growth potential, and the impacts of management activities on forest biomass and carbon can be evaluated, tested, modeled, and readily visualized (Zhang and Shi 2004; Zhang et al. 2004; Zhen et al. 2013).

In this study, we attempted to depict the spatial distribution of forest carbon storage in Heilongjiang Province, P.R. China. The objectives of this study were (1) to fit the ordinary least squares (OLS) model, linear mixed model (LMM) and geographically weighted regression (GWR) model to the data of forest carbon storage; (2) to compare the fit and performance of the three models; (3) to assess the spatial autocorrelations and heterogeneity of the model residuals; and (4) to validate the model predictions using an independent data set.

Materials and methods

Study Area

Heilongjiang Province (121º11′ E to 135º05′ E and 43º25′ N to 53º33′ N) is located in northeast China (Fig. 1) with a total land area of 454,000 km2. The terrain of the province slopes downward from the northwest to the southeast and includes four prominent mountain ranges, viz. Da Xing’an Mountain (Greater Xing’an Range), Xiao Xing’an Mountain (Lesser Xing’an Range), Zhangguangcai Range, and the Wanda Range. About 36% of the province has elevation higher than 300 m. The Sanjiang Plain in the northeast and the Songnen Plain in the west are important parts of the largest plain in China, covering 37% of the province at elevations ranging from 50 to 200 m. The study area has a northern temperate continental monsoon climate. The annual average temperatures are -5.0 °C–5.0 °C. The annual average precipitation is 400–670 mm and 75% of the precipitation occurs between June and August.

The province has a total of forest area over 20.8 million hectares (about 45.8% of the total land area of the province) and the forest coverage rate is 45.7%. Total volume of living trees was 1.76 billion m3and the average volume per hectare was 78.6 m3. For timber forests, the area of young and mid-aged stands reached to 82.2%, while the mature and over-mature forests accounted for only 6.4% of the area (HLJFOREST. 2014). Major tree species include Korean pine (Pinus koraiensis Sieb.et Zucc.), spruce (Picea koraiensis Nakaki and Picea jezoensis (Sieb.et Zucc.) Carr.), fir (Abies nephrolepis (Trautv.) Maxim.), larch (Larix gmelinii (Rupr.) Rupr. and Larix olgensis Henry), Mongolian pine (Pinus sylvestris .var. mongolica Litv.), basswood (Tilia amurensis Rupr. and Tilia mandshurica Rupr.et Maxim.), Mongolian oak (Quercus mongolica Fisch. ex Ledeb.), birch (Betula platyphylla Suk., Betula costata Trautv. and Betula davurica Pall.), maple (Acer mono Maxim.), Manchurian ash (Fraxinus mandshurica Rupr.), Manchurian walnut (Juglas mandshurica Maxim.), Amur cork tree (Phellodendron amurense Rupr.), poplar (Populus davidiana Dode., Populus ussuriensis Kom.), elm (Ulmus propinqua Koidzand Ulmus laciniata (Trautv.) Mayr.), and other minor species. Korean pine is the dominant species, spruce and fir dominate in high elevation areas (Zhou et al. 2013).

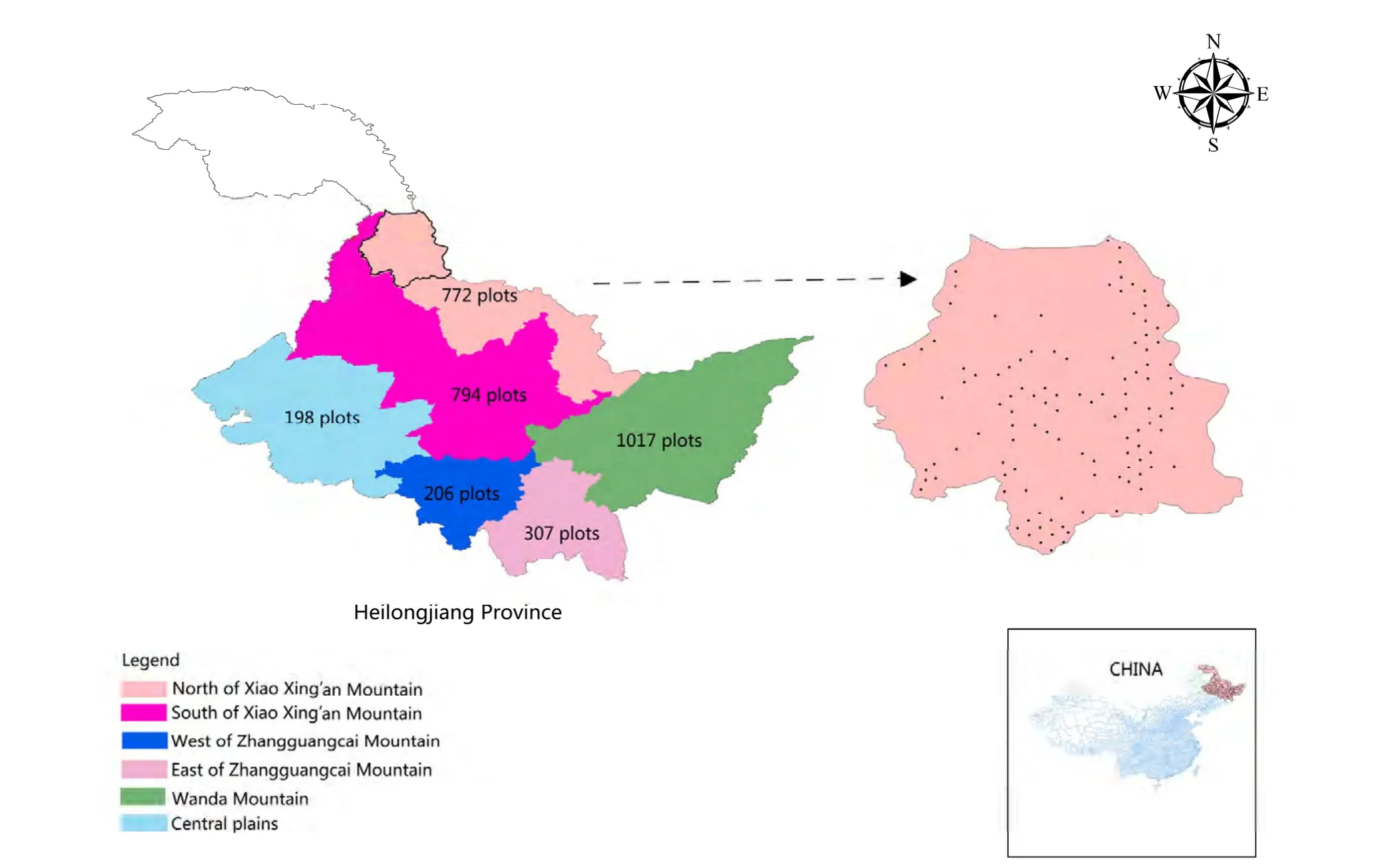
Fig. 1: Map of the study area in Heilongjiang, China, and the geographical location of the six regions with the number of sample plots.

Biomass data and climatic variables

The study area was divided into six regions: (1) the northern region of the Xiao Xing’an Mountain, (2) the southern region of the Xiao Xing’an Mountain, (3) the western region of the Zhangguangcai Mountain, (4) the eastern region of the Zhangguangcai Mountain, (5) Wanda Mountain, and (6) Central Plains. The stand and tree data used in this study were collected from these six regions in 2010 from 3038 permanent sample plots (each 0.06 ha in size) monitored by the Chinese National Forest Inventory (CNFI) and Key Ecological Benefit Forest in Heilongjiang province. The geographic location and topographic descriptors were recorded for each plot. Stand and tree variables were measured and recorded to describe elevation (m), slope (°), slope aspect, number of tree species, number of trees by species, diameter at breast height (DBH) (cm), and individual height of all living trees (HT) (m). Other stand and tree variables were then computed on a per hectare basis including number of trees per hectare (TPH) (trees/ha), volume of living trees (m3/ha), average age of living trees (year), vegetation coverage (%), and others. The entire data set for 3038 plots was randomly split into model fitting data (n =2379 plots) and model testing data (m = 659 plots).

The carbon content of individual trees includes four components - stem, branch, foliage, and root. In a sample plot, the biomass models (unpublished) based on the Tang et al. method (2001) were used to compute the biomass of the four components (i.e., stem, branch, foliage, and root ) for each species based on tree DBH. The carbon content of each component was then obtained by multiplying the component biomass by the corresponding component carbon content rate, which was tested with a C/N analyzer using the collected samples of each tree component. Thus, the individual tree carbon content was obtained by adding up the carbon contents of the four tree components. The sum of all individual trees in the same plot was the total carbon content (ton) for each sample plot, and the carbon content per hectare (t/ha) was calculated as the total carbon content of the sample plot divided by the plot area.

One-year meteorological records were collected from the 59 weather stations in the provinces of Heilongjiang, Jilin, and Inner Mongolia in 2010. In this paper, temperature and precipitation data were considered to be the main factors, as they influenced tree growth and, thereby, carbon sequestration of the forest. Kriging interpolation was used to obtain the temperature and precipitation data from these weather stations for each sample plot in this study at interpolation precision >85%.

The purpose of this study was to describe the spatial distribution and pattern of forest carbon storage via regression models. The dependent variable was carbon content (C) for each plot (ton / ha). A number of stand and tree variables were tested and five were selected as the predictors in the models: average diameter of living trees (DBH), number of trees per hectare (TPH), elevation (Elev), slope (Slope), and the product of precipitation and temperature (Rain_Temp). DBH represented the size and/or age of the stand. TPH represented the density of the stand. Elev and Slope represented the geographic characteristics of the stand. The Rain_Temp represented the climatic features of the stand.

The basic statistics of the variables are listed in Table 1.

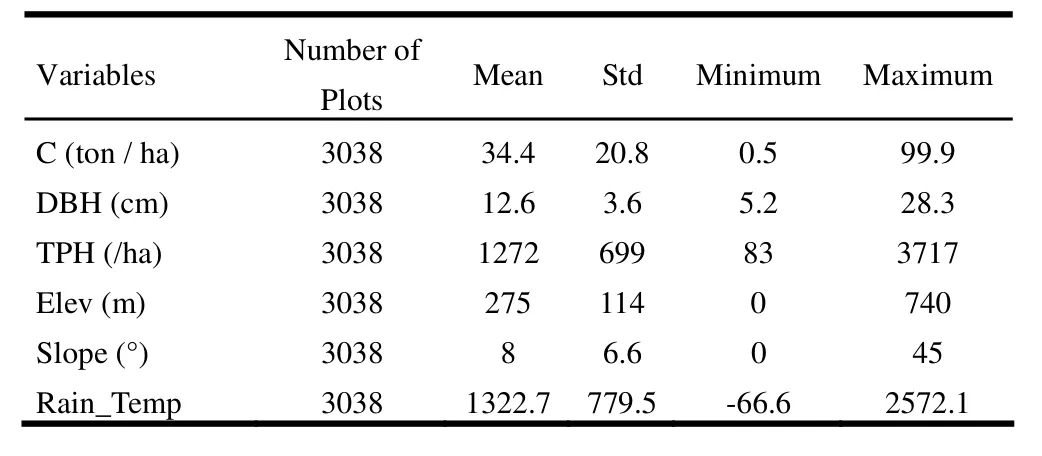
Table 1: Descriptive statistics of variables used in this study

Regression models

In this study we used three regression models – ordinary least squares model, linear mixed model, and geographically weighted regression model. We briefly describe the modeling techniques below.

(1) Ordinary Least Squares (OLS). Suppose we have a set of n observations on a dependent or response variable Y, and p independent or predictor variables X. The relationship between Y and X can be regressed using OLS as follows:

where β is a vector of unknown fixed-effects model coefficients to be estimated from the data and ε is the model error term which follows N(0, σ2). The OLS estimator can be obtained by

The relationship represented by eq [1] is assumed to be universal or constant across the geographic area.

(2) Linear Mixed Model (LMM). LMM is expanded from OLS and can be expressed as

where Y is a vector of response variable, X is a matrix of fixed-effects predictors, β is a vector of unknown fixed-effects model coefficients, Z is a known design matrix of random-effects, γ is a vector of unknown random-effects parameters, and ε is the random error term. It is assumed: (1) E(γ) = 0 and Var (γ) = G is a covariance matrix of random-effects, (2) E(ε) = 0 and Var (ε) = R is a covariance matrix of model residuals, (3) Cov (γ, ε) = 0, and (4) both γ and ε are normally distributed, and (4) the variance of Y is given byand can be estimated by setting up the random-effects design matrix Z and specifying the covariance structures for G and R. In this case, OLS is no longer the best parameter estimation method, while maximum likelihood methods are usually used to obtain β and γ (Little et al. 2006).

(3) Geographically Weighted Regression (GWR). To investigate the spatial variation of a regression relationship, the data must be collected with the location coordinates (ui, vi) for each observation i, i = 1, 2, …, j, …, n. j is neighboring observation of i. The local information leads to estimate the localized regression coefficients of the relationship of interest (Fotheringham et al. 2002). The underlying model for GWR is expressed as below:

where Yiis the response variable, Xkis a set of p predictor variables (k = 1, 2, …, p), β0(ui, vi), β1(ui, vi), …, βp(ui, vi) are the regression coefficients for the kth predictor variable and ith location. εiis the random error term whose distribution is N(0, σ2I), with I denoting an identity matrix. The aim of GWR is to obtain estimates of these functions for each predictor variable and each geographic location i. The estimation procedure of GWR is as follows: (i) draw a circle of a given radius around one particular location i (the center), (ii) compute a weight (wij) for each neighboring observation j according to the distance dijbetween the location j and center i, and (iii) estimate the model coefficients using weighted least-square regression such that

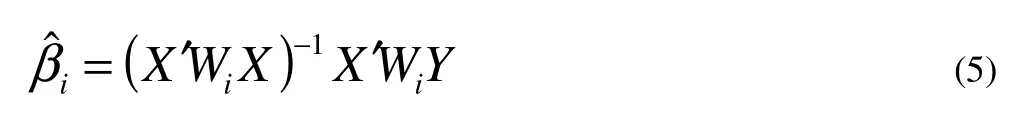
where the weight matrix Wiis

The weighting function is defined by the kernel type and the size of kernel (bandwidth), which determines the geographical weight of the jth neighboring observation at the ith regression point. The weight should decrease gradually as the distance between i and j increases, until to a constant or zero. The estimation of model coefficients is highly related to kernel size, so the choice of kernel is an important consideration. If Wi= I (i.e., identity matrix), each observation in the data has a weight of unity and the GWR model is equivalent to the ordinary least squares model (Fotheringham et al. 2002; Guo et al. 2008).

Two types of kernel functions are commonly used: (1) Gaussian kernel with fixed bandwidth, and (2) adaptive methods with bi-square kernel. There are different approaches to determining the bandwidths of the spatial kernel functions. (1) Pre-selected bandwidth, (2) use the range of the variogram for the ordinary least-squares (OLS) model residuals, (3) minimizing Akaike’s Information Criterion (AIC), (4) minimizing cross-validation function (CV), (5) multiple bandwidths in an adaptive kernel function. In general, there is no significant difference between the bandwidths obtained from the cross-validation and AIC methods (Guo et al. 2008).

Therefore, we obtain a set of estimates of spatially varying parameters without specifying a function form for the spatial variation. Essentially, GWR lets the data speak for themselves when estimating each regression coefficient βikfor each geographic location i and each independent variable k (Fotheringham et al. 2002; Guo et al. 2008; Zhang and Gove 2005).

Localized sample mean

Given a geographic location with the coordinates (ui, vi) and a bandwidth, the spatial weight matrix Wi(Eq. (6)) can be calculated using a selected kernel function. Then, a descriptive statistic like the sample mean of any variable can be computed at each location i using the neighboring information as follows:

The process moves from location to location across the study area until this localized sample mean is computed for each and every location. It describes the spatial heterogeneity of the variable at a local scale and can be visualized on a map to illustrate the spatial distribution of the variable (e.g., forest carbon storage) (Brunsdon et al. 2002; Ma et al. 2012).

Model specification

The following multiple linear model was used to regress forest carbon content (C) on the 5 predictors by the OLS, LMM and GWR models:

where β0–β5were regression coefficients to be estimated from data, and ε was the model residual, which was defined as the difference between the observed and predicted C. In this study, the three models were fitted using the model fitting data (n = 2379 plots). SAS 9.3 (SAS Institute Inc. 2011) was used for fitting both OLS and LMM models. The OLS model (Eq. (1)) was used as the benchmark for model comparison. For the LMM model (Eq. (3)), the six regions were treated as the fixed effects because the study was concerned with Heilongjiang Province only, whereas the spatial autocorrelations among the sample plots within the regions were modeled by the covariance matrix R (Little et al. 2006). The GWR model (Eq. (4)) was fitted by GWR 4.0 software available at the following link http://www.st-andrews.ac.uk/geoinformatics/, using an adaptive bisquare kernel function with the golden section search (automated). The best bandwidth size was 25 km (Fotheringham et al. 2002). The localized sample mean of the forest carbon was computed by GWR 3.0, using the same kernel function and bandwidth (25 km) as the GWR model above (Ma et al. 2012). GWR 4.0 added new prediction capability compared to GWR 3.0, but it eliminated functions that compute local statistics. So we used both GWR 3.0 and GWR 4.0.

Model assessment

The overall model fit was evaluated by three statistics including the coefficient of determination (R2), mean squared error (MSE), and Akaike’s Information Criterion (AIC). However, both model R2and MSE may be biased because they are based on the assumption of independence of observations, which may be violated by spatial data as analyzed in this study. They are at best approximate measures of the model fit. Hence, AIC is more appropriate because the likelihood function does not rely on the assumption of independent error terms (Littell et al. 2006).

It is well known that spatial effects include spatial autocorrelation and heterogeneity. Ignoring spatial effects in a modeling process causes misleading significance tests and sub-optimal model prediction (Zhang et al. 2009). To investigate the spatial autocorrelations in the model residuals, both global and local spatial autocorrelation indices (i.e., Moran’s I) were computed for the residuals of OLS, LMM and GWR models. The global Moran’s I is defined by

where xiand xjrepresent the observed values of the species richness changes at atlas blocks I and j,is the average value of xi across the study area, and wij(d) is the spatial weight measure within a given bandwidth d. If distance between block j and subject block i is smaller or equal to d, the wij(d)=1; otherwise wij(d) =0. The expectation of global Moran’s I is -1/(n-1). The Moran’s I value will be larger than -1/(n-1) if positive spatial autocorrelation exists which indicates that similar values, either high or low values, are spatially clustered within a certain distance d. Values of Moran’s I below -1/(n-1) indicate negative spatial autocorrelation and the observed values tend to be dissimilar within distance d. Moran’s I approximates 0 when the observed values are ar-ranged randomly and independently over space.

We used a local indicator of spatial association (LISA) to allow for the decomposition of global Moran’s I into localized values. The local form of Moran’s Iiis defined by:

We used local Moran’s Iito detect the local clustering around an individual atlas block location and to test for spatial nonstationarity. A positive local Moran’s Iiimplies a spatial clustering of similar values (either high or low) around an individual location, whereas a negative local Moran’s Iiimplies a clustering of dissimilar values around an individual location.

In this paper, the global Moran’s I was computed for a range of bandwidths from 5 to 35 km at 5 km intervals, which described the overall spatial autocorrelation in the model residuals at different spatial scales. The local Moran’s I, one of the local spatial autocorrelation indices (LISAs), was computed at the optimal bandwidth (25 km) for each residual of OLS, LMM and GWR models. The spatial distribution of local Moran’s I was used to show the "hot spots" of residual clusters (i.e., the same sign of model residuals) and "cold spots" of residual clusters (i.e., the opposite sign of model residuals) across the study area. These“hot spots” indicated undesirable characteristics of the models (Zhang and Gove 2005, Zhang et al. 2005, 2009).

To quantify the spatial heterogeneity of model residuals, intra-block spatial variances were computed for the residuals of OLS, LMM and GWR models at block sizes ranging from 5 to 25 km at 5 km interval. The intra-block spatial variances were used to illustrate the local spatial variability in the model residuals for each model (Zhang et al. 2009).

Model prediction and validation

The data used in this study were split into model fitting and model testing data sets. A total of 659 plots were randomly selected for testing the ability of model prediction for the three models. The following statistics were used to evaluate model predictions:

where Ciis the observed forest carbon of a testing plot,is the predicted forest carbon for the testing plot by each of the three models, p (=5) is the number of parameters, and m (= 659) is the size of the testing data set.

Results

Spatial distribution of localized mean of forest carbon storage

The local descriptive statistic (i.e., localized mean) of forest carbon storage was computed using the optimal bandwidth 25 km across the study area (Fig. 2). Localized mean was a very effective method to test the spatial patterns of change in forest carbon storage with the change of distribution of observations. It showed more detailed information and reflected the geographic distribution trend of forest carbon storage. Fig. 2 illustrates that the forest carbon storage in our study area was not evenly distributed, but varied greatly from place to place. The northeast and south regions were mountainous with higher elevations, steeper slopes and denser forest stands so that forest carbon storage had much higher mean values (about 40 t/ha). In contrast, the west regions were located in the Central Plain at lower elevations with flatter slopes and mostly included urban residential areas with low tree densities. This region had low overall forest carbon storage (<25 t/ha). It was evident that forest carbon storage differed significantly over the study area, illustrating heterogeneous spatial distribution of forest carbon storage.

Fig. 2: Localized mean of the forest carbon storage. The dots are the sample plots

Model fitting and coefficients

The response variable (forest carbon content) was regressed on the five predictors, average diameter (DBH), stand density (TPH), elevation (Elev), slope (Slope) and the product of precipitation and temperature (Rain_Temp). The overall model fit statistics are listed in Table 2. It was clear that the local model, GWR, fit the data much better with lower AIC, MSE and R2than the two global models (OLS and LMM). The LMM model also fit the data better than the OLS model because the LMM model incorporated spatial heterogeneity via random effects across the six regions.

Table 2: Model fitting and testing statistics of the three models (OLS, LMM and GWR).

The estimates of model coefficients, standard errors (SE), and p-values of the five predictors are listed in Table 3 for the two global models (OLS and LMM). Each of the model coefficients was statistically significant at α = 0.05 for both models, except the estimate forin the LMM model, which yielded a p value of 0.5362.was the product of precipitation and temperature (Rain_Temp). This showed that these climate features were similar across the six regions. It seemed that the standard errors of the slope coefficients of the OLS model were smaller than those of the LMM model, indicating that OLS might have under-estimated standard error due to violation of the assumption of independence of observations (spatially correlated forest carbon content) (Table 3).

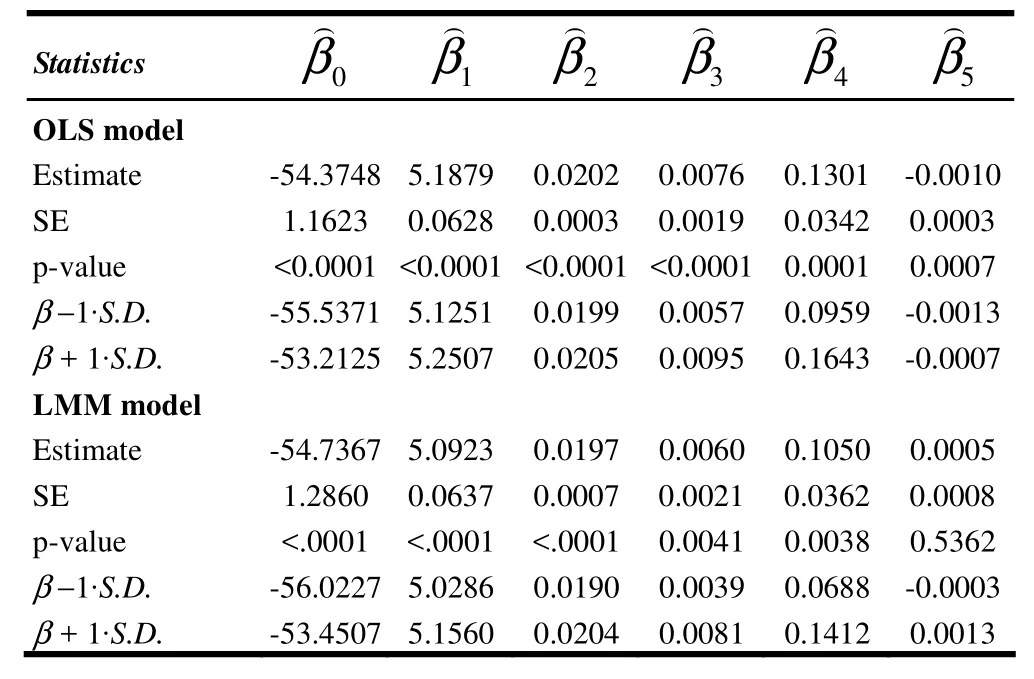
Table 3: Model coefficient estimates, standard error (SE), and p-values of the OLS and LMM models.

The GWR model produced model coefficients that varied geographically, i.e., one set of model coefficients was produced for each geographic location. Table 4 summarizes the descriptive statistics of these local model coefficients, including mean, minimum, 25% quartile (Q1), median, 75% quartile (Q3), and maximum. The medians of the GWR coefficients were similar to those produced by the OLS and LMM models. However, the localized GWR coefficients had wide ranges across the study area. This can be evaluated by the facts that 50% of the GWR coefficients fell between Q1(25% quartile) and Q3(75% quartile), while about 68% of the OLS or LMM coefficients, assuming normal distribution, should be within ±1 standard deviation. If the inter-quartile range of the GWR local coefficients is greater than that of ±1 standard deviation of the equivalent global parameter, the relationship under study might be spatially non-stationary (Fotheringham et al. 2003; Zhang et al. 2004). For example, the inter-quartile range of the GWR local(DBH) was 4.9116–5.5745, which was outside the range of ±1 standard deviation of the OLS model (5.1251–5.2507) and of the LMM model (5.0286–5.1560). Similarly, the inter-quartile range of the GWR local(TPH) was 0.0177 – 0.0239, which was outside the range of ±1 standard deviation of the OLS model (0.0199 –0.0205) and of the LMM model (0.0190 – 0.0204) (Tables 3 and 4). Therefore, it was evident that the relationship between forest carbon content and five predictors was indeed spatially non-stationary or heterogeneous (Fotheringham et al. 2003; Zhang et al. 2004).

Table 4: Model coefficient estimates of the GWR model.

The spatial variation of each model coefficient of the GWR model is illustrated in Fig. 3. The relationship between forest carbon and the 5 predictors varied from region to region across the study area. In general, the model coefficients of DBH () and TPH () were positive over the study area, while the model coefficients of Elev (), Slope (), and Rain_Temp () ranged from negative to positive depending on the region (Table 4). For example, in the west regions,(DBH) was 1.87–3.25,(TPH) was 0.006–0.016,(ELev) was -0.10–-0.01,(Slope) was -9.55–-7.69, and(Rain_Temp) was -0.11 – -0.07. In the southeastern regions,(DBH) was 5.95–7.99,(TPH) was 0.02–0.03,(ELev) was 0.06–0.16,(Slope) was -0.32–2.39, and(Rain_Temp) was 0.05–0.09. Fig. 3 clearly demonstrates that the signs and magnitudes of these regression coefficients varied by geographic region, indicating the different impacts of the five predictors on the forest carbon content, depending on the forest conditions and topographic features.

Fig. 3: Contour maps of the model coefficient estimates from the GWR model at the band width 25 km: (a) Intercept , (b) for DBH, (c) for TPH, (d) for Elev, (e) for Slope, and (f) for Rain_Temp.

Spatial autocorrelation in model residuals

Global Moran’s I and Z-values were computed for the model residuals of the three models based on a bandwidth of 25 km for GWR (Table 2). Z-values are simply standard deviations. According to the Z-value, the model residuals of both OLS and LMM had significant spatial autocorrelation (Z-value >2.58, significant at α = 0.01), while the spatial autocorrelation of the GWR residuals was not significant (Z-value <1.96, at α = 0.05). Thus, the local modeling technique, GWR, successfully reduced the spatial autocorrelation in model residuals (Table 2).

Fig. 4 illustrates the spatial correlogram of the model residuals for the three models across a range of lag distances (5–35 km). The residuals of the OLS model presented much larger spatial autocorrelations than did those of LMM and GWR at each lag distance tested. The LMM model significantly reduced spatial autocorrelation compared with OLS, but it was relatively large, especially at smaller spatial scales (5–15 km). On the other hand, the spatial autocorrelation of the GWR model residuals always approached zero at different spatial scales (Fig. 4).

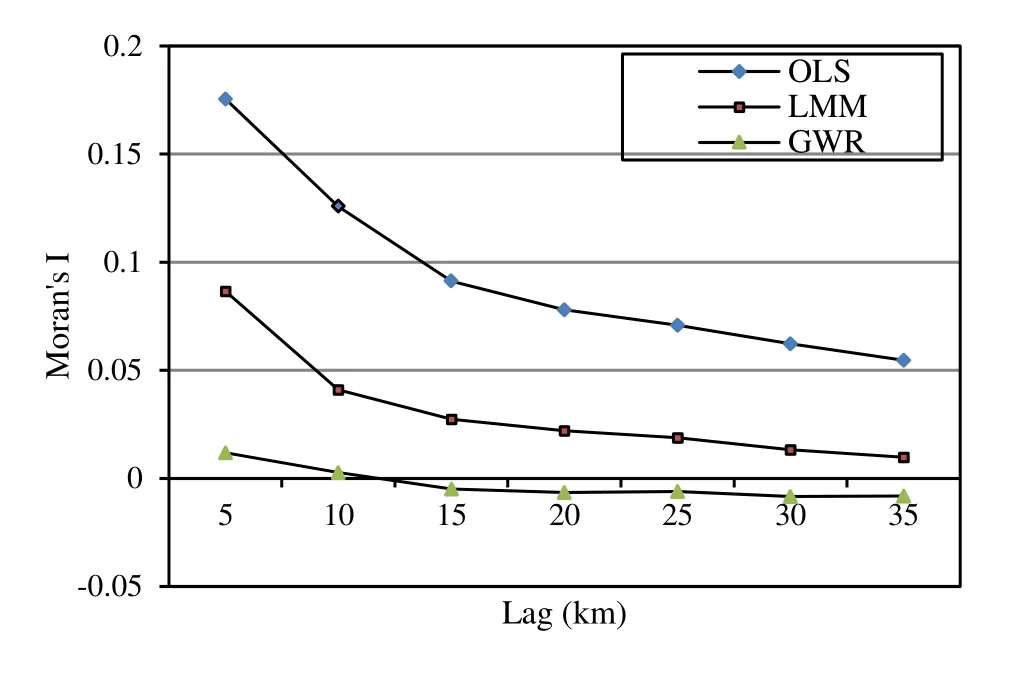
Fig. 4: Correlogram of the model residuals of the three models.

Local Moran’s I was computed for residual from each of the three models. However, because the entire study area was too large and the number of plots too many to show for all plots, we chose to show local Moran’s I for the plantation plots only as a demonstration in Fig. 5. It was clear the values of local Moran’s I for the OLS model residuals were larger and more positive (black dots in the figure) across the area, indicating clusters (hot spots) of either under- or over-prediction by the OLS model residuals. The values of local Moran’s I for the GWR model residuals were much smaller and more negative (circles in the figure), indicating the clusters (cold spots) of opposite signs of the model residuals, which was a more desirable characteristic of the model because neighboring residuals had opposite signs and might have resulted in a zero average for any local area (Zhang and Gove 2005; Zhang et al. 2005, 2009).

Spatial heterogeneity in model residuals

Fig. 6 illustrates the intra-block variances in model residuals for the three models, which represented the local spatial variability or heterogeneity for a given block size. The two global models (OLS and LMM) had similar sizes and patterns of the intra-block variances across different block sizes, indicating that although the LMM model reduced the spatial autocorrelation in the model residuals, it did not reduce spatial heterogeneity in the model residuals. On the other hand, the intra-block variances of the GWR model residuals were much smaller than those of the two global models at different spatial scales. Our results are consistent with those of other studies (e.g., Zhang et al. 2005, 2009).

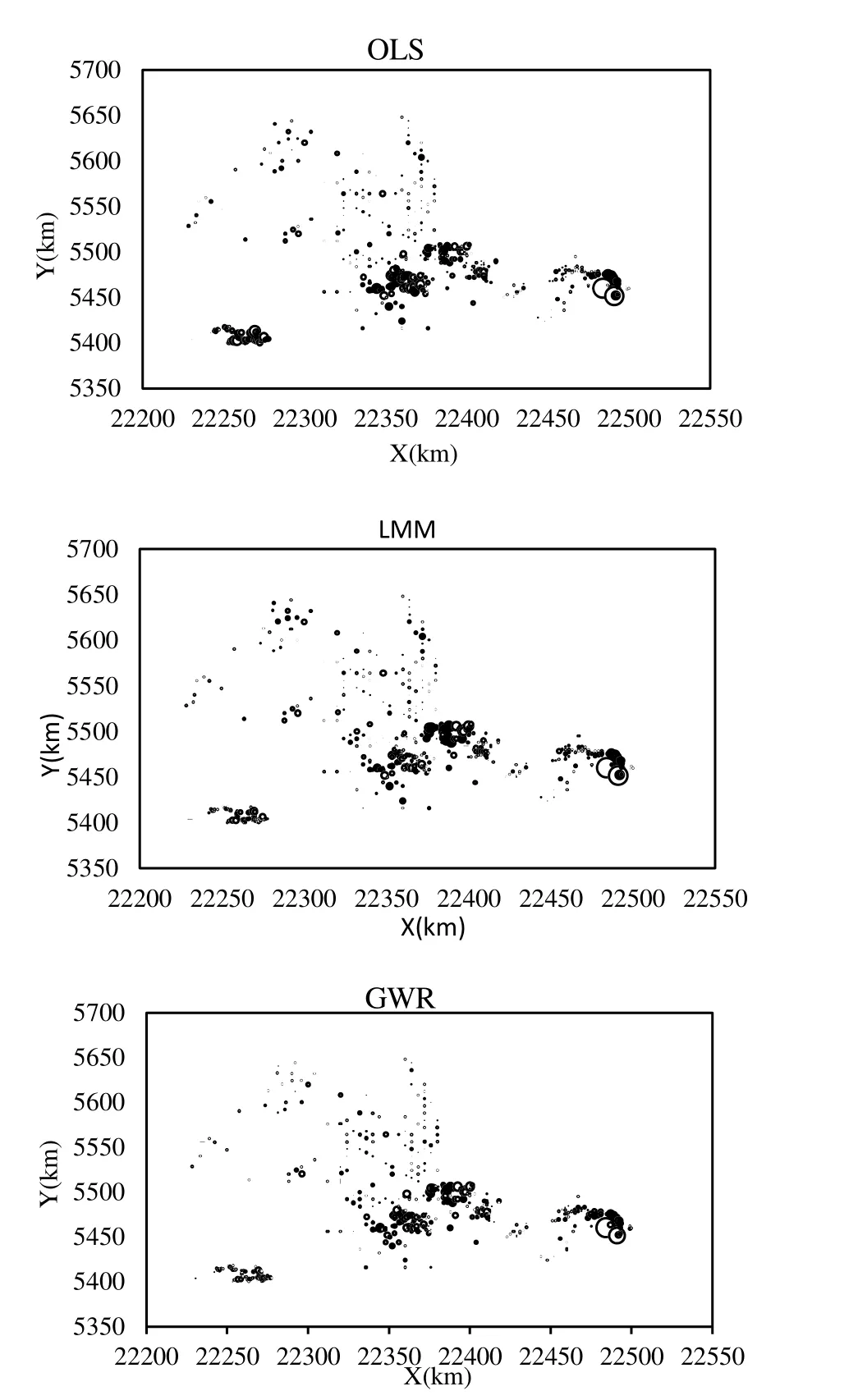
Fig. 5: Spatial distribution of local Moran’s I of model residuals for the plantation plot: OLS, LMM and GWR. The size of the symbols (black dot and circle) is proportional to the values of Moran’s I. The black dots represent positive values (hot spots), and the circles represent negative values (cold spots).

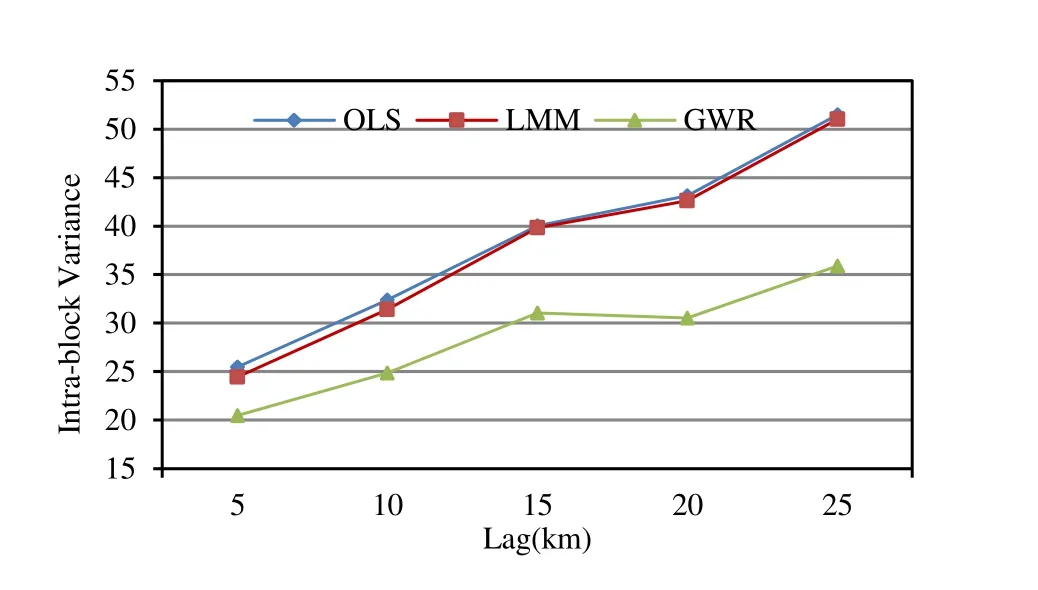
Fig. 6: Intra-block variances of the model residuals of the three models.

Model prediction

Table 2 shows the MSE and RMSE of model predictions for the model testing data for the three models. In terms of model RMSE, the GWR model reduced the model prediction error about 10.6% from the OLS model, and 7.2 % from the LMM model, while the LMM model reduced the prediction error 3.5% from the OLS model.

Discussion

In this study, we used both global and local regression models to investigate the relationship between forest carbon storage and stand, environment and weather factors or predictors. This information can be used to predict forest carbon storage to provide useful information on forest management planning and decision making. One of the main purposes in this study was to learn the spatial variation of forest carbon storage across Heilongjiang province.

Our five predictors had statistically significant effects on the amount and distribution of forest carbon storage. In both global models (OLS and LMM), DBH and TPH were the most important stand variables for our study area. The model coefficients DBH () and TPH () were both positive (Table 3), indicating that larger DBH and higher stand density would sequester more carbon in the forests. Our results are consistent with those of other studies. For example, Brown (2002) found that DBH alone explained more than 95% of the variation in aboveground carbon content in tropic forests. Among topographic factors, elevation and slope were most important. However, the model coefficients for Elev () and Slope () were positive (Table 3), indicating higher elevations and steeper slopes would support more stored carbon, while other studies found negative coefficients for elevation (Lal 2005). This can be explained in our study area by the fact that the stands at lower elevations on flatter slopes typically had lower stand densities due to human activities and thus had lower forest carbon content. For weather factors, the interaction of rainfall and temperature was more important than each factor alone in this study. Rainfall is always a strong factor influencing the growth of trees, and, consequently, carbon sequestration. Temperature directly affected rainfall, soil water content, tree growth and carbon storage.

The discussion above was based on the model coefficients of the global models (OLS and LMM), which were constants across the study area. Given the diverse forest conditions and topographic features of the stands, these constant model coefficients would not be able to accurately describe the impacts of the five predictors on forest carbon for different local areas. On the other hand, the GWR model provided localized model coefficients which can be visualized using GIS technology (Johnston et al. 2001) to show more detailed information on the relationship between the forest carbon storage and predictors. Fig. 3 shows the spatial variations of the model coefficients. It is clear that the impacts of these predictors on forest carbon vary from region to region in the study area. In general, the model coefficients of DBH () and TPH () were still positive over the study area, but the magnitudes of the coefficients varied substantially by region. The model coefficients Elev (), Slope (), and Rain_Temp () ranged from negative to positive depending on the region. Thus, the constant model coefficients of the global models (OLS and LMM) not only provided biased prediction for a specific area, but also misrepresented the relationship between forest carbon stock and stand and environment factors. The localized model coefficients of the GWR model provided detailed information on the influence of micro-site variation and the impacts of management activities on tree growth and forest carbon storage in aid to both management planning and decision making (Zhang and Shi 2004; Lu and Zhang 2012; Zhen et al. 2013).

Analyses of spatial autocorrelation in the model residuals indicated that the violation of the OLS model assumption of independence of observations was clear and significant, and this led to biased hypothesis testing on the model coefficients. Although the LMM model was designed to deal with spatial autocorrelation, our results showed the LMM model residuals retained significant spatial autocorrelation (Table 2), especially at smaller spatial scales (Fig. 4), unlike in other studies (Zhang et al. 2005; 2009). On the other hand, the GWR model successfully reduced levels of spatial autocorrelation in the model residuals while yielding desirable spatial patterns for model residuals (Fig. 6). However, GWR did not directly incorporate spatial autocorrelation into the modeling process because it assumed N(0, σ2I) for the model error term, but GWR explicitly took spatial locations into account and emphasized local variation in the relationships between variables. Our results were consistent with findings in the literature (e.g., Zhang et al. 2005; 2009).

The intra-block variances (local spatial variability) showed that the GWR model residuals had much smaller spatial heterogeneity than those of the two global models across different block sizes. And the difference between LMM and OLS was not significant. This was also a bit surprising because the literature showed that LMM greatly reduces spatial heterogeneity in model residuals for tree growth data (e.g., Zhang et al. 2005; 2009). The reason may be that the spatial variation among the sample plots for forest carbon storage was much larger than the spatial variation between stands of trees so that the LMM model in this study reduced to some degree both spatial autocorrelation and heterogeneity.

The GWR methodology also has weaknesses and limitations such as the influence of outliers (local parameter estimates can be strongly affected by a single outlier or outliers), weak data problem (a small number of neighbors available within a given bandwidth, especially if a “pre-selected” bandwidth is small), and lack of independence among the model parameter estimates (Zhang et al. 2004; Zhang and Shi 2004; Shi et al. 2006). Nevertheless, given the variety and complexity of forest ecosystems, this local modeling technique does provide high-precision and visualizable information for planning silvicultural and management activities and reduces the cost and labor to obtain more carbon.

Conclusions

In this study we investigated the spatial distribution of forest carbon storage in Heilongjiang Province, P.R. China, and the relationship between forest carbon stocks and five stand and environmental parameters, viz. tree diameter (DBH), number of trees per hectare (TPH), elevation (Elev), slope (Slope) and the product of precipitation and temperature (Rain_Temp). We fitted two global models (OLS and LMM) and a local model (GWR). All predictors were statistically significant, indicating they were important factors influencing forest carbon storage. The two global models provided one predictive model for the entire study area and it might have inaccurately estimated forest carbon content for local areas because the stand conditions and topographical features varied greatly over the province.

The GWR model significantly outperformed the two global models in model fitting and model prediction because it successfully reduced both spatial autocorrelation and heterogeneity in model residuals. Therefore, the model coefficients were available for each location and could be mapped to illustrate spatial heterogeneity in the regression relationship under study at different spatial scales. The GWR model could estimate forest carbon storage for sites located anywhere in Heilongjiang province, even where no plots were sampled. Consequently, the influence of stand conditions and micro-environment features, as well as the impacts of silvicultural management on forest biomass and carbon can be evaluated, tested, modeled, and readily visualized. The localized and detailed information would be valuable for planning management regimes and decision making.

Anselin L, Bera AK. 1998. Spatial dependence in linear regression models with an introduction to spatial econometrics. Statistics Textbooks and Monographs, 155: 237-290.

Baral A, Guha GS. 2004. Trees for carbon sequestration or fossil fuel substitution: the issue of cost vs. carbon benefit. Biomass and Bioenergy, 27: 41-55.

Bronson DR, Gower ST, Tanner M, Linder S, Van Herk I. 2008. Response of soil surface CO2 flux in a boreal forest to ecosystem warming. Global Change Biology, 14: 856-867.

Brown S. 2002. Measuring carbon in forests: current status and future challenges. Environmental Pollution, 116:363-372.

Brunsdon C, Fotheringham AS, Charlton M. 1999. Some notes on parametric significance tests for geographically weighted regression. Journal of Regional Science, 39:497-524.

Brunsdon C, Fotheringham AS, Charlton M. 2002. Geographically weighted summary statistics - A framework for localized exploratory data analysis. Computers, Environment and Urban Systems, 26:501-524.

Brunsdon C, Fotheringham AS, Charlton ME. 1996. Geographically weighted regression: A method for exploring spatial nonstationarity. Geographical Analysis, 28: 281-298.

Charlton M, Fotheringham S, Brunsdon C. 2009. Geographically weighted regression. White paper. National Centre for Geocomputation. National University of Ireland Maynooth.

Chi GQ. 2010. The impacts of highway expansion on population change: An integrated spatial approach. Rural Sociology, 75:58-89.

Chi W, Qian XY. 2009. The role of education in regional innovation activities and economic growth: spatial evidence from China. Available at: http://mpra.ub.uni-muenchen.de/id/eprint/15779

Daoyi G, Peijun S. 2004. Inter-annual changes in Eurasian continent NDVI and its sensitivity to the large-scale climate variations in the last 20 years. Acta Botanica Siniea, 46:186-193.

Du HQ, Zhou GM, Fan WY, Ge HL, Xu XJ, Shi YJ, Fan WL. 2010. Spatial heterogeneity and carbon contribution of aboveground biomass of moso bamboo by using geostatistical theory. Plant Ecology, 207:131-139.

Echalar F, Gaudichet A, Cachier H, Artaxo P. 1995. Aerosol emissions by tropical forest and savanna biomass burning: Characteristic trace elements and fluxes. Geophysical Research Letters, 22: 3039-3042.

Espa G, Arbia G, Giuliani D. 2013. Conditional versus unconditional industrial agglomeration: disentangling spatial dependence and spatial heterogeneity in the analysis of ICT firms’ distribution in Milan. Journal of Geographical Systems, 15: 31-50.

Fahey TJ, Woodbury PB, Battles JJ, Goodale CL, Hamburg SP, Ollinger SV, Woodall CW. 2009. Forest carbon storage: ecology, management, and policy. Frontiers in Ecology and the Environment, 8: 245-252.

Falkowski P, Scholes RJ, Boyle EEA, Canadell J, Canfield D, Elser J, Gruber N, Hibbard K, Högberg P, Linder S. 2000. The global carbon cycle: A test of our knowledge of earth as a system. Science, 290: 291-296.

Fang JY, Chen AP, Peng CH, Zhao SQ, Ci LJ. 2001. Changes in forest biomass carbon storage in China between 1949 and 1998. Science, 292: 2320-2322.

Fotheringham AS, Brunsdon C, Charlton M. 2002. Geographically weighted regression: the analysis of spatially varying relationships. Wiley and Sons, p.269.

Fotheringham AS, Charlton ME, Brunsdon C. 2001. Spatial variations in school performance: A local analysis using geographically weighted regression. Geographical and Environmental Modeling, 5: 43-66.

Granier A, Ceschia E, Damesin C, Dufrêne E, Epron D, Gross P, Lebaube S, Le DV, Le GN, Lemoine D. 2000. The carbon balance of a young beech forest. Functional Ecology, 14: 312-325.

Guo L, Ma Z, and Zhang L. 2008. Comparison of bandwidth selection in application of geographically weighted regression: a case study. Canadian Journal of Forestry Research, 38: 2526-2534.

Hazlett PW, Gordon AM, Sibley PK, Buttle JM. 2005. Stand carbon stocks and soil carbon and nitrogen storage for riparian and upland forests of boreal lakes in northeastern Ontario. Forest Ecology and Management, 219: 56-68.

Heath LS, Smith JE. 2000. An assessment of uncertainty in forest carbon budget projections. Environmental Science and Policy, 3:73-82.

HLJFOREST. 2014. http://www.hljforest.gov.cn/

Houoatow RA. 1997. Terrestrial carbon storage: global lessons for Amazonian research. Ciencia e Cultura Sao Paulo, 49: 58-72.

Johnston K, Ver JM, Krivoruchko K, Lucas N. 2001. Using ArcGIS geostatistical analyst. Esri Redlands.

Kurz WA, Apps MJ. 1999. A 70-year retrospective analysis of carbon fluxes in the Canadian forest sector. Ecology Applications, 9: 526-547.

Kurz WA, Stinson G, Rampley GJ, Dymond CC, Neilson ET. 2008. Risk of natural disturbances makes future contribution of Canada's forests to the global carbon cycle highly uncertain. Proceedings of the National Academy of Sciences, 105: 1551-1555.

Law BE, Thornton PE, Irvine J, Anthoni PM, Van TS. 2001. Carbon storage and fluxes in ponderosa pine forests at different developmental stages. Global Change Biology, 7: 755-777.

Lindesay JA, Andreae MO, Goldammer JG, Harris G, Annegarn HJ, Garstang M, Scholes RJ, Van BW. 1996. International geosphere-biosphere programme/international global atmospheric chemistry SAFARI-92 field experiment: Background and overview. Journal of Geophysical Research, 101: 23521-23523, 530.

Littell RC, Milliken WW, Stroup RD, Wolfinger A. 2006. SAS for mixed models. 2ndEd. Cary, USA: SAS Press, p.441.

Lu J, Zhang L. 2011. Modeling and prediction of tree height-diameter relationships using spatial autoregressive models. Forest Science, 57: 252-264.

Lu J, Zhang L. 2012. Geographically local linear mixed models for tree height-diameter relationship. Forest Science, 58:75-84.

Ma Z, Zuckerberg B, Porter WF, Zhang L. 2011. Use of localized descriptive statistics for exploring the spatial pattern changes of bird species richness at multiple scales. Applied Geography, 32: 185-194.

Myeong S, Nowak DJ, Duggin MJ. 2006. A temporal analysis of urban forest carbon storage using remote sensing. Remote Sensing and Environment, 101: 277-282.

Neilson ET, MacLean DA, Meng F, Arp PA. 2007. Spatial distribution of carbon in natural and managed stands in an industrial forest in New Brunswick, Canada. Forest Ecology and Management, 253: 148-160.

Nelson R, Krabill W, Tonelli J. 1988. Estimating forest biomass and volume using airborne laser data. Remote Sensing and Environment, 24: 247-267.

Phillips DL, Brown SL, Schroeder PE, Birdsey RA. 2000. Toward error analysis of large-scale forest carbon budgets. Global Ecology and Biogeography, 9: 305-313.

Pickett S, Cadenasso ML. 1995. Landscape ecology: spatial heterogeneity in ecological systems. Science, 269: 331-334.

Sales MH, Souza CM, Kyriakidis PC, Roberts DA, Vidal E. 2007. Improving spatial distribution estimation of forest biomass with geostatistics: A case study for Rondônia, Brazil. Ecological Modeling, 205: 221-230.

SAS Institute, Inc. 2011. SAS/STAT Users’ guide. Version 9.3. Cary, NC: SAS Institute, Inc..

Shi H, Zhang L. 2003. Local analysis of tree competition and growth. Forest Science, 49: 938-955.

Shi H, Zhang L, Liu J. 2006. A new spatial-attribute weighting function for geographically weighted regression. Canadian Journal of Forest Research, 36: 996-1005.

Smith JE, Heath LS, Skog KE, Birdsey RA. 2006. Methods for calculating forest ecosystem and harvested carbon with standard estimates for forest types of the United States. United States Department of Agriculture, Forest Service, Northeastern Research Station.

Sohngen B, Mendelsohn R. 2003. An optimal control model of forest carbon sequestration. American J. Agricultural Economics, 85: 448-457.

Tang SZ, Zhang HR, Xu H. 2000. Study on establish and estimate method of compatible biomass model. Scientia Silvae Sinicae, 36: 19-27. (in Chinese)

Valentini R, Matteucci G, Dolman AJ, Schulze E, Rebmann C, Moors EJ, Granier A, Gross P, Jensen NO, Pilegaard K. 2000. Respiration as the main determinant of carbon balance in European forests. Nature, 404: 861-865.

Wofsy SC, Harriss RC. 2002. The North American Carbon Program (NACP). Report of the NACP Committee of the US Interagency Carbon Cycle Science Program. US Global Change Research Program, Washington, DC 59.

Zhang L, Bi H, Cheng P, Davis CJ. 2004. Modeling spatial variation in tree diameter–height relationships. Forest Ecology and Management, 189: 317-329.

Zhang L, Gove JH. 2005. Spatial assessment of model errors from four regression techniques. Forest Science, 51:334-346.

Zhang L, Gove JH, Heath L. 2005. Spatial residual analysis of six modeling techniques. Ecological Modeling, 186: 154-177.

Zhang L, Ma Z, Guo L. 2009. An evaluation of spatial autocorrelation and heterogeneity in the residuals of six regression models. Forest Science, 55: 533-548.

Zhang L, Shi H. 2004. Local modeling of tree growth by geographically weighted regression. Forest Science, 50: 225-244.

Zhen Z, Li FR, Liu ZG, Liu C, Zhao YL, Ma ZH, Zhang L. 2013. Geographically local modeling of occurrence, count, and volume of downwood in Northeast China. Applied Geography, 37: 114-126.

Zhou XJ, Wang FL, Wu YY, Na JH, Pan HS, Wang Y. 2013. Analysis of temperature change characteristics of Heilongjiang Province, northeast China and whole country in recent 60 years. Journal of Natural Disasters, 22(2):124-129. (in Chinese).