Spatial distributions of tropical tree species in northern Vietnam under environmentally variable site conditions

Nguyen Hong Hai • Kerstin Wiegand • Stephan Getzin

Introduction

A central question in forest ecology is how to understand the processes and mechanisms that control species coexistence and community structure, especially at various spatial scales. These relevant issues have been addressed in numerous studies. Barot (2004) highlighted the impact of both exogenous and endogenous factors on the spatial and temporal distributions of tree species. Other studies investigated intra- and inter-specific interactions (Callaway and Walker 1997; Bruno et al. 2003), dispersal limitation (Hubbell 1979), negative density dependence (Wright 2002), or habitat preference (Condit et al. 2000). Tilman (2004) emphasized that spatial patterns of trees may be explained by environmental niche effects and trade-offs among species due to dispersal and competitive ability.

Environmental heterogeneity (such as different soil types, rock outcrops, or streams) makes spatial pattern analysis more complicated because it confounds biotic and abiotic effects (Li and Reynolds 1995; Wiens 2000). Dispersal limitation is emphasized as a potential mechanism for separating species in space and reducing competitive exclusion (Seidler and Plotkin 2006). Besides that, a patchy distribution of trees can also be caused by habitat preference where demographic processes and limiting resources may simultaneously influence spatial patterns (Wagner and Fortin 2005; Getzin et al. 2008). Spatial aggregation of a species can be induced by limited seed dispersal or patchy habitat conditions or by both factors (Webb and Peart 2000).

In addition, negative density dependence or self-thinning is a prominent mechanism for regulating population dynamics and facilitating species coexistence (Wright 2002). This mechanism has been considered by a negative density of conspecific distance relations in forest dynamics such as recruitment, growth or survival (Condit et al. 1992; Peters 2003; Uriarte et al. 2004a). Density comparisons of life history stages ranging from seedlings to adults provide evidence of self-thinning. However, self-thinning cannot always be observed in species with distinct habitat preferences (McDonald et al. 2003) or in tree fall gaps (Augspurger 1984).

Direct tree-tree interactions are often observed at small scales while at large scales, they can be obscured by environmental factors (Wiegand et al. 2007). The challenge is to separately consider first-order effects (i.e., habitat preference of tree species) and second-order effects (i.e., competition or facilitation within or between species). Disentangling these effects makes it possible to find evidence for different hypotheses about species coexistence and structuring of plant communities at different spatial scales (Callaway and Walker 1997; Wiegand et al. 2007). Interestingly, Getzin et al.(2008) found that plant ecology, in terms of plant population dynamics and pattern formation, may differ between homogeneous and heterogeneous sites, beyond the purely statistical effects of heterogeneity. Given that most studies focus on homogeneous sites, there is an urgent need to compare spatial patterns in homogeneous and heterogeneous forest sites.

In this study, we analyzed spatial patterns and associations of six dominant tree species in the tropical evergreen forest in Babe National Park, in northern Vietnam. We investigated four aspects of tree distribution: environmental heterogeneity, spatial distribution patterns of species, inter-specific associations, and conspecific associations between life stages. We used methods of point-pattern analysis and compared patterns to different null hypotheses. Significant deviation from null hypotheses was evaluated by confidence envelopes , which were constructed with Monte Carlo simulations (Stoyan and Stoyan 1994; Diggle 2003). This approach has shown theoretical and practical advantages in previous studies on spatial-pattern analysis of tree distribution (Wiegand et al. 2007; Getzin et al. 2008; Martinez et al. 2010; Wang et al. 2010; Lan et al. 2012). We expect this study to contribute to the understanding of spatial patterns and environmental effects on species distributions in the tropical forests.

Materials and methods

Study area

The study was conducted at Babe National Park (NP), in northern Vietnam. It is located approximately 250 km north of Hanoi and 75 km north-west of Backan City. This area receives an annual rainfall of 1378 mm and a mean temperature of 220C and mean humidity of 83.3%. Babe natural lake has a surface-water area of about 500 ha and is surrounded by straight cliffs of Karst Mountains. Two plots were chosen in the core zone of the park where human impact is minimal (Fig. 1).

Fig. 1: Map of Babe NP and location of study plots (Source: the NP)

The study site is classified as tropical evergreen lowland forest, which is one of several rainforest sub-types in the area (Rcfee 2011). The soil has a thick layer of yellow-brown ferralsol with clay to sandy clay particle-size classes.

Data collection

We selected two study sites that differed in geomorphological characteristics such as slope position (hillfoot and hillside); rock outcrops (low and high abundance); and slope (Table 1). In each site, a 1-ha plot was established and subdivided into 100 10 m × 10 m subplots. The diameter at breast height (dbh; at 1.3 m above the ground); tree coordinates (x,y); and species name were recorded for all woody plants with dbh ≥2.5 cm. Stem-mapping of individuals was done using a laser distance measurement (Leica Disto D5) and compass. All individual trees were divided into three size classes: “juvenile” (dbh <5 cm), “sub-adult” (5 cm≤ dbh <10 cm) and “adult” (dbh ≥10 cm).

Table 1: Environmental characteristics of the two 1-ha forest plots in Babe NP.

For most of the analyses, we focused on the five most dominant tree species in each plot. Four of these five species occurred at both plots: Diospyros sylvatica (Ebenaceae); Burretiodendron hsienmu (Tiliaceae); Hydnocarpus kurrzii (Flacourtiaceae);

Syzygium wightianum (Myrtaceae).Two species occurred on one plot only: Taxotrophis ilicifolia (Moraceae) and Streblus macrophyllus (Moraceae). H. kurrzi, T. ilicifolia and S. macrophyllus are shadetolerant species, which develop well on thick and humid soils, while B. hsienmu and S. wightianum are shadeintolerant species (FIPI 1996).

Statistical analysis

The K-function and pair-correlation function

The K-function is defined as the expected number of points occurring within distance r of a randomly chosen point and normalized by the intensity λ of the point pattern (Ripley 1976; Diggle 2003; Wiegand and Moloney 2004; Illian et al. 2008). K(r) is the cumulative distribution function up to a given radius r. We used the square root transformation of the K-function:

The univariate pair-correlation function g(r) is related to the widely used K-function. It is a non-cumulative distribution function and presents the expected number of points in a ring at distance r from an arbitrary point divided by the intensity of the pattern (Stoyan and Stoyan 1994; Wiegand and Moloney 2004). It is calculated as:

The parameter g(r) indicates whether a pattern is (1) random (complete spatial randomness CSR; g(r) = 1), (2) clumped (g(r) > 1) or (3) regular (g(r) < 1) at a given radius r. It can be extended to describe the relationship between two point patterns. The bivariate pair-correlation function g12(r) represents the expected density of points of pattern 2 at distance r from an arbitrary point of pattern 1, divided by the intensity of pattern 2 (Wiegand and Moloney 2004). Therefore, g12(r) = 1 indicates independence (no interaction) between two types of points, and g12(r) >1 indicates that there are, on average, more points of type 2 at distance r from points of type 1 than expected under independence, hence showing attraction between these two types of points. Similarly, g12(r) <1 indicates repulsion between the two types of points.

Null models

We used a two-step approach as suggested by Dixon (2002) and Wiegand and Moloney (2004): (1) compare the estimated L- or g-function (equation 1, 2) with the expected values from an appropriate null model, which is potentially useful for the underlying point processes; and (2) hypothesistesting based on approximate confidence envelopes constructed by Monte Carlo simulations of the stochastic process.

Complete spatial randomness (CSR): CSR is a commonly used null model for univariate analysis. It assumes no interaction between the points of a pattern, for example locations of individual trees of a given species or size class (Wiegand and Moloney 2004). The intensity of trees in the pattern is constant over the study plot, meaning that trees can occur at any position and are independent from other trees.

Heterogeneous Poisson process (HP): HP is used if the distribution of trees is of varying intensity within the pattern. This may be caused by obstacles like rock outcrops, streams or differences in soil. In such cases, the null model of CSR is not suitable for exploration of second-order characteristics (e.g., tree-tree interactions). The heterogeneous Poisson process is an alternative to account for the first-order moment (i.e., large-scale variation in habitat quality). The constant intensity assumed for CSR is replaced by an intensity function that varies with tree location but preserves the independence of tree positions from each other. For simulations with the grid-based Programita software, a circular moving window with radius R is placed at a provisional point of a random cell (x,y), then a probability density is computed and retained for this point. The procedure is repeated for all N points of the pattern (Wiegand and Moloney 2004).

Random labeling: If we want to investigate whether or not pattern 1 and pattern 2 are created by the same stochastic process, locations of points in the joined pattern (1 + 2) are fixed and then the locations of point pattern 2 are randomized among fixed locations (Wiegand and Moloney 2004). The random-labeling null model tests if a second stochastic process randomly affects the individuals of a population or if there is a spatial pattern in this second process (Goreaud and Pelissier 2003). Two test statistics, g12-g11and g21-g22, were examined. While g12-g11shows different intensities of pattern 2 points around pattern 1 points compared to pattern 1 points around themselves in circles with radii r, g21-g22evaluates whether type 2 points tend to be surrounded by points of type 1 (g21-g22> 0) or more by other points of type 2 (g21-g22< 0).

Analysis 1: Environmental heterogeneity

An initial and fundamental step in spatial pattern analysis of plant communities is to identify if environmental conditions on the site are homogeneous or heterogeneous. Tree densities may vary between locations due to different environmental conditions and tree-tree interactions. These two effects are difficult to distinguish.

Our study sites were chosen to account for and compare environmental effects assuming homogeneity of environmental conditions at plot 1 and heterogeneity at plot 2. Getzin et al. (2008) argue that adult trees of all species have exploited all available sites. Thus, the spatial pattern of all adults should clearly reveal the effect of environmental heterogeneity on tree distribution.

On the heterogeneous site, we expected the intensity of trees to vary at large scales. Therefore, the g-function should not approach the expected value 1 for scales which are beyond direct interactions of trees. The L-function should strongly increase and not converge to 0 for large scales because it is an accumulative function of r (Wiegand and Moloney 2004). Comparing results from the g- and L-functions is considered an advantage over visual interpretation of habitat heterogeneity.

Analysis 2: Species distributions

We used the univariate pair-correlation function to investigate spatial patterns of the six dominant species in both plots. Null models were CSR for plot 1 and HP for plot 2. A radius R = 30 m for the circular moving window was chosen to factor out the large-scale structure of the pattern in plot 2. Under the HP null model, the locations of the focal tree were displaced randomly within the neighborhood R. This process eliminated neighborhood patterns at small scales r < R while preserving larger-scale patterns (by randomizing the pattern using its intensity).

We used a displacement band R = 30 m that is similar to typical scales at which tree-tree interactions have been found (Hubbell et al. 2001; Peters 2003; Uriarte et al. 2004b). We combined the non-parametric Epanechnikov kernel for the intensity function with a spatial resolution of 1 m. We expected interactions of tree species at small scales and environmental heterogeneity at larger scales.

Analysis 3: Species associations

To identify inter-specific association of tree species (i.e., repulsion or attraction), we performed the bivariate analyses with null models appropriate for environmental conditions. For the homogeneous site, pattern 1 was fixed and pattern 2 was randomized using CSR null model (independence null model). For the heterogeneous site, we kept the location of trees in the first pattern fixed and randomized the location of trees in the second pattern using a HP null model. As in analysis 2, non-parametric kernel, bandwidth R = 30 m and 1 m resolution were used. Mutual interactions between pairs of species were checked, for example species 1 against species 2 (g12) and species 2 against species 1 (g21) because interactions between species can be asymmetric (Wiegand et al. 2007).

Analysis 4: Species association between life stages

To investigate spatial associations between life stages of conspecific trees, we used the bivariate pair-correlation function with null model of random labeling. We considered conspecific associations between adults (pattern 1) and individuals of early life stages (pattern 2) for each tree species. Parameter g12-g11< 0 shows a lower intensity of young trees than of adults in the vicinity of adults, while g21-g22< 0 indicates that there is additional aggregation of young individual independent from conspecific adults.

All point-pattern analyses were performed with the grid-based software Programita (Wiegand and Moloney 2004) and the R package Spatstat 2.12.2 (Team 2010). Significant departures from the null models were evaluated by constructing approximately 95% confidence envelopes using the fifth lowest and fifth highest values of 199 Monte Carlo simulations.

Results

Species composition and characteristics

In plot 1, 17 species were found from 12 families, and in plot 2, 26 species belonging to 14 families. Fourteen species occurred in both plots, including four dominant species with more than 50 individuals (Table 2).

Table 2: Characteristics of 6 dominant tree species (> 50 individuals/plot) in the two 1-ha plots, Babe NP. dbh (diameter at breast height); NN-nearest neighbor distance.

Two dominant tree species were found in one plot only: T. ilicifolia and S. macrophyllus. For analysis 1, all adults of all species were used. In all other analyses, we analyzed the six dominant species only. In plot 1, H. kurzii had the largest basal area and mean dbh. B. hsienmu had the lowest density of the analyzed species, but had a large basal area of 6.41 m2/ha. T. ilicifolia and D. sylvatica were the most frequent species in plot 1.

On average, trees in plot 2 were smaller than those in plot 1. Densities of S.wightianum and D. sylvatica were similar in both plots. For S. wightianum, the considerably larger dbh in plot 1 resulted in the basal area being twice as large as in plot 2. H. kurzzi, D. sylvatica, T. ilicifolia, S. macrophyllus and S. wightianum showed a reverse J-shaped distribution in both plots, with the number of individuals gradually decreasing with larger diameters (Fig. 2). The size distribution of B. hsienmu differed between the plots: unimodal in plot 1 (Fig. 2a) and reversed J-shaped in plot 2 (Fig. 2b). In both plots, B. hsienmu had no individual in size class 60-70 cm.

Fig. 2: dbh distribution of 6 dominant tree species in the two 1-ha plots. x-axes display size classes in 10 cm intervals, y-axes display number of individual trees.

Environmental heterogeneity

For both plots, we compared the spatial distributions of all adult trees with dbh ≥ 10 cm (Fig. 3) to the null model of CSR to investigate if the patterns showed large-scale heterogeneity. Then, the compatibility of Plot 2 to the null model of the HP was checked with bandwidth R = 30 m.

In plot 1, the L-function showed no large-scale departure from CSR (Fig. 4a). The g-function fluctuated around g = 1 and fell completely inside the confidence envelopes for all scales (Fig. 4b). This indicated large-scale homogeneity in the plot. In contrast to this, in plot 2, the L-function showed a clear departure from CSR for scales r > 5 m (Fig. 4c) and did not approach g = 0. In addition, the g-function was significantly > 1 for scales larger than 13-25 m and did not approach g = 1 (Fig. 4d), providing evidence of large-scale heterogeneity at plot 2. Moreover, the spatial arrangement fit very well with the null hypothesis of HP with R = 30 m (Fig. 4e-f) when analyzed by L-function and the pair-correlation function. Therefore, for all further spatial-pattern analyses, we applied the homogeneous g-function for plot 1 and the heterogeneous g-function for plot 2.

Fig. 3: Spatial distributions of all adult trees (dbh ≥ 10 cm) in the two 1-ha plots (Size of circles is proportional to dbh of trees). The unit of (x,y) axes is meters.

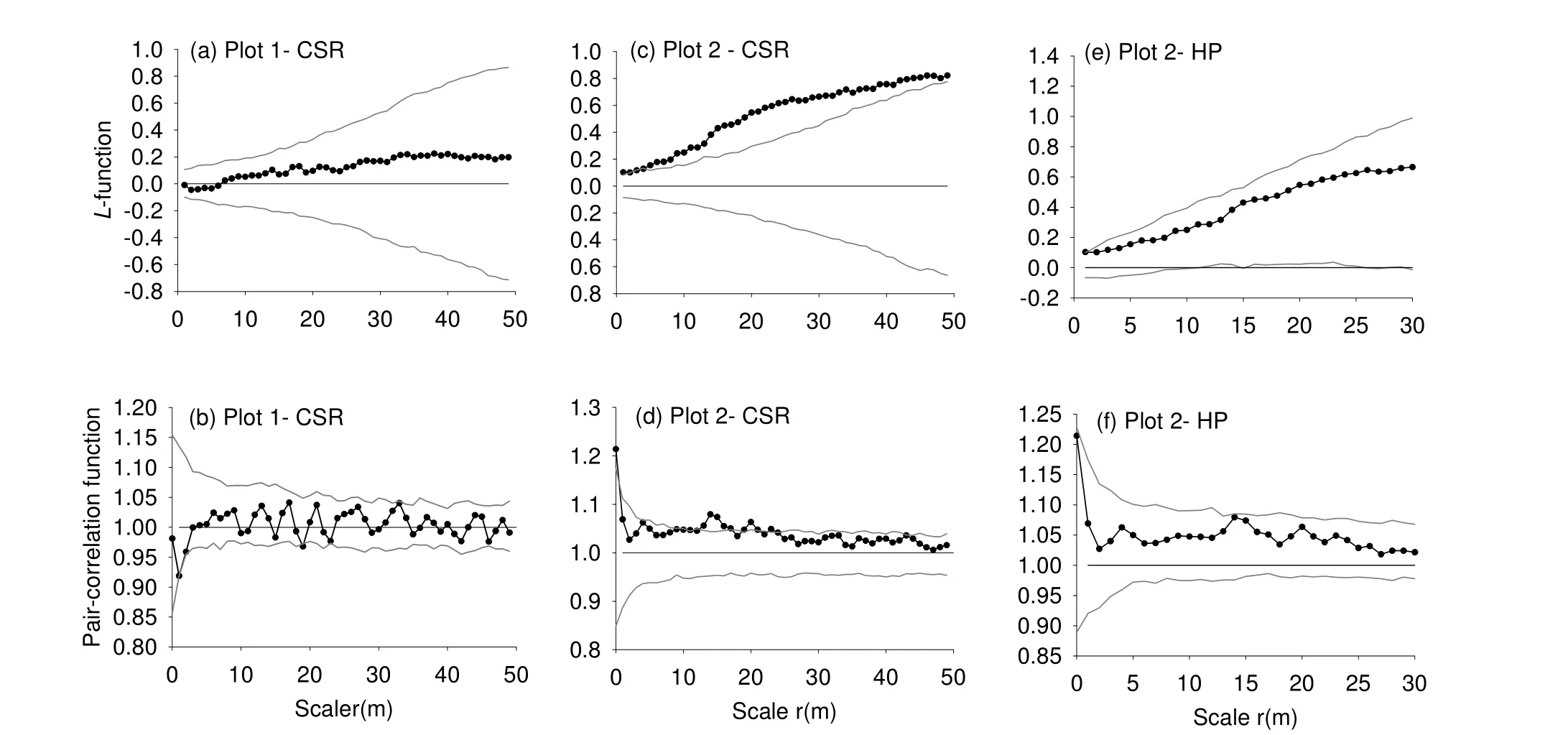
Fig. 4: Spatial patterns of all adult trees (dbh ≥ 10 cm) in two plots using L-function (upper row, 4a, c, e) and the univariate pair-correlation function (lower row, 4b, d, f). Null models: CSR (a-d) and HP with R = 30 m (e-f). Black lines are observed patterns; grey lines are approximate 95% confidence envelopes.

Species distributions

Spatial patterns of dominant species in both sites are shown in Fig. 5. All dominant species were found in clustered distribution at various scales, except B. hsienmu in the heterogeneous site. The aggregation intensity declined clearly with increasing spatial scales. All five species were clustered significantly in the homogeneous plot (Fig. 5a-e) at various scales under CSR null model. No significant pattern was found at scales larger than 30 m. H. kurzii, D. sylvatica and S. wightianum were aggregated up to large scales (Fig. 5a, c, d). B. hsienmu was random at small scales and aggregated at 8-10 m and at larger scales of 20-25 m (Fig. 5b). T. ilicifolia showed a strong clustered distribution over the entire range of scales up to 27 m (Fig. 5e).

In the heterogeneous plot, B. hsienmu (inset, Fig. 5i) was the only dominant species with random distribution. The four remaining dominant species showed aggregated distributions under the HP null model with bandwidth R = 30 m (insets, Fig. 5f, j-l). In contrast to the homogeneous plot, no significant aggregation was found at scales larger than 15 m. This indicates that environmental heterogeneity led to different scales in spatial aggregation of a species.

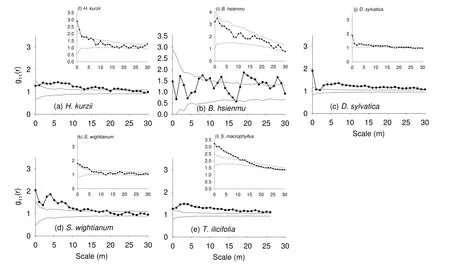
Fig. 5: Spatial patterns of dominant tree species shown by the pair correlation function g11 with different null models: CSR at the homogeneous site (a-e) and HP at the heterogeneous site (insets, f-m). Black lines are observed patterns; grey lines are approximate 95% confidence envelopes.

Inter-specific associations

Species associations were analyzed at scales 0-30 m by using the bivariate pair-correlation function. In both plots, we performed 40 bivariate point-pattern analyses for all pairs of dominant species. Overall, attraction occurred more frequently in the homogeneous site, while independence and repulsion predominated in the heterogeneous site (appendix 1).

In the homogeneous site, 10 pairs showed attraction, with eight pairs independence and two pairs repulsion (appendix 1). Fig. 6 shows examples of species maps and bivariate patterns in plot 1. All species pairs had symmetric interactions. T. ilicifolia showed negative associations with all other species. D. sylvatica and S. wightianum had positive associations with the three remaining species. B. hsienmu and H. kurzii were independent in species interactions. T. ilicifolia was found only in the lowest parts of the plot where it gets higher soil moisture, but is separated from other species. In contrast, B. hsienmu and S. wightianum are shade intolerant and found in the highest parts of the site.

In the heterogeneous site, four species pairs showed attraction, 11 pairs independence and five pairs repulsion (appendix 1). Fig. 7 shows some examples of species maps and bivariate association patterns in this plot. Two pairs of species exhibited asymmetric interactions: B. hsienmu versus S. macrophyllus and versus S. wightianum, respectively. S. macrophyllus showed only negative and independent associations with other species. As in the homogeneous plot, S. wightianum had positive associations with B. hsienmu and D. sylvatica. B. hsienmu and H. kurzii showed independent associations with the other species, with the exception of S. macrophyllus. S. macrophyllus repulsed all species except B. hsienmu. In the heterogeneous plot, more asymmetric species interactions were found. Moreover, the number of significant associations was lower and the number of independent species pairs higher than in the homogeneous plot.

Fig. 6: Examples of species distribution maps and bivariate patterns in the homogeneous site. Pattern 1 is displayed as solid circles and pattern 2 as open circles. The pair correlation function g12 was performed under null model that pattern 1 was fixed and pattern 2 randomized. Black lines are observed patterns; grey lines are approximate 95% confidence envelopes.

Fig. 7: Examples of species distribution maps and bivariate patterns in the heterogeneous site. Pattern 1 is displayed as solid circles and pattern 2 as open circles. The pair correlation function g12 was performed under null model that pattern 1 was fixed and pattern 2 randomized under HP process. Black lines are observed patterns; grey lines are approximate 95% confidence envelopes.

Intra-specific associations between life stages

Spatial associations between life stages of six dominant tree species in both plots were analyzed with the bivariate pair-correlation function under null model of random labeling. Two test statistics, g12-g11and g21-g22, were used to find conspecific associations between adult and younger growth stages (appendix 2).

In the homogeneous plot, B. hsienmu was not analyzed because of low abundance (less than 30 individuals in each growth stage). In H. kurzii and T. ilicifolia, g12-g11< 0 predominated in associations between adults and trees at early life stages, indicating that there were fewer young individuals in the vicinity of potential parent trees. In D. sylvatica and S. wightianum, g12-g11= 0 showed that adults and individuals at early growth stages exploited environmental conditions in a similar way. There was only one species (S. wightianum) where juveniles were concentrating at higher density around their adults. In H. kurzii, T. ilicifolia and S. wightianum, g21-g22< 0 dominated, suggesting that there was additional clumping of young individual trees independent from their potential parent trees. In D. sylvatica, g21-g22= 0 showed no higher density of young individuals in the vicinity of theirparents.

At the environmentally heterogeneous site, only adults and sub-adult stages of B. hsienmu were considered, but all life stages of the other four species were considered. The test statistic g12-g11< 0 in all cases of D. sylvatica and S. wightianum indicated a lack of young trees around adult trees, except in D. sylvatica where sub-adults concentrated at a higher density around conspecific adults (g12-g11> 0). Moreover, g12-g11= 0 predominated in all analyses of H. kurzii, S. macrophyllus and B. hsienmu, showing that young and adult trees exploited available resources in the same way. Meanwhile, the test statistic g21-g22< 0 in most of the analyzed cases showed that individuals at young growth stages were aggregated independently of their conspecific adults.

Discussion

Environmental heterogeneity

The main goals of our study are to detect effects of environmental heterogeneity on spatial patterns and distributions of tree species. For comparative analyses, we use two fully mapped 1-ha plots that have four dominant tree species in common, but differ in environmental homogeneity. Our results clearly show a difference in dbh distributions between the individuals of a species on the homogeneous and the heterogeneous site. This indicates exogenous effects on successful establishment and mortality.

In the homogeneous site, H.kurzii and S. wightianum present a wide range of dbh classes with decreasing numbers of individuals in the larger size classes suggesting successful establishment and self-thinning in homogeneous site conditions. B. hsienmu seems to be well developed in the heterogeneous site with a reverse J-shape distribution which contrasts to a lack of individual trees in small size classes of the homogeneous plot. That may be caused by its ecological preference of direct sunlight as a shade-intolerant tree.

In terms of spatial patterns, the density of all adult trees in the homogeneous plot is equal over the entire plot, implying homogeneity of environmental conditions. This indicates that the species’ spatial distribution depends only on their specific ecology, such as seed dispersal or habitat preference. In the heterogeneous site, species distribution is affected not only by the species’ecology but also by inhomogeneous site conditions. The inhomogeneous pair-correlation function shows the “pure” effect of heterogeneity at scales up to the bandwidth R = 30 m. To detect the “true” density dependence of trees, it is necessary to separate confounding effects. Using adult trees to factor out environmental heterogeneity is a simple and efficient approach, thus it has been used in previous studies, for example, Getzin et al. (2008) and Zhu et al.(2009).

Species distributions

In our study, all dominant tree species in both plots exhibit aggregated patterns. This is similar to the results of previous studies, where most tropical tree species were found to have a clumped or random distribution (He et al. 1997; Condit et al. 2000; Bunyavejchewin et al. 2003; Zhang et al. 2013). Spatially heterogeneous habitat or limited seed dispersal can lead to patchy distribution but may not affect all species (He et al. 1997; Harms et al. 2000; Bunyavejchewin et al. 2003; Zhang et al. 2010).

The univariate analyses of six dominant species reveal significant environmental effects on the spatial scale of species demographics: H. kurzii, D. sylvatica and S. wightianum are aggregated up to larger scales under homogeneous site conditions than under heterogeneous conditions. T. ilicifolia and S. macrophyllus are aggregated at large scales indicating their habitat preferences and/or well dispersed seeds. Furthermore, T. ilicifolia is a humidity-demanding species, favoring relatively wet and shady habitat, and is distributed at the lowest area of plot 1. H. kurzii, S. macrophyllus and D. sylvatica are shade tolerant species (FIPI 1996) and they grow under forest canopy. Moreover, D. sylvatica is a dioecious species and can be pollinated by wind (Somanathan and Borges 2000) which can explain its strong aggregation. B. hsienmu is mainly dispersed by gravity and has a poor regeneration (Wang et al. 1986) leading to a low number of young trees (plot 1) in a random pattern (plot 2).

Light conditions are sufficient for S. wightianum in canopy gaps since it is a light-demanding species (FIPI 1996; Gunatilleke et al. 2006). Direct intra-specific interactions occur within scales of 30 m and disappear at larger scales (shown by Plot 1). This finding is consistent with previous studies using individual-based analyses, where local neighborhood effects occurred within 20 or 30 m (Hubbell et al. 2001; Uriarte et al. 2004b; Wiegand et al. 2007).

Inter-specific associations

Attraction between species predominates in the homogeneous site while repulsion is more frequent in the heterogeneous site. Positive association suggests that species have similar habitat preference or occupy different forest layers. The latter leads to different regeneration requirements (Yamada et al. 2006). The attractions between B. hsienmu - S. wightianum (plot 1, both light demanding but B. hsienmu is a slow-growing species), D. sylvatica - S. wightianum (in both plots, D. sylvatica is shade tolerant and a sub-canopy tree) and B. hsienmu - D. sylvatica can be explained by their ecological differences. Negative interactions emphasize the effect of habitat segregation onto species association in forest stands. Among the three main limiting plant resources, soil nutrients, water availability and light (Debski et al. 2002), we assume that soil humidity and light are the driving factors in the study sites.

Segregated distribution or topographical habitat differentiation can be reasons for negative interactions (North et al. 2004; Pizano et al. 2011). This could explain why T. ilicifolia (plot 1) and S. macrophyllus (plot 2), whose distributions are separated, show negative associations with most other species. Bunyavejchewin et al.(2003) found that negative associations provide indirect evidence of habitat segregation. H. kurzii shows differences between the plots regarding its associations with other species: it is attracted by other species in the homogeneous site while it is independent from other species in the heterogeneous site. Habitat segregation is based on the niche differentiation of resources; therefore a segregated habitat could be suited for different species and leads to less inter-specific associations (Harms et al. 2001). The fact that independence dominates in species associations at the heterogeneous site might be due to the effects of biotic and abiotic factors. Assertion of species independence may be a good approximation for species-rich communities, but still remains unclear in communities with low species richness (Wiegand et al. 2012).

Intra-specific associations between life stages

Bivariate analyses between conspecific life stages provide a closer view on intra-specific associations. In some species, g12-g11< 0 implies a lack of young individuals around conspecific adults, such as H. kurzii, T. ilicifolia (plot 1) and D. sylvatica, S. wightianum (plot 2). Moreover, g12-g11= 0 in the remaining species indicates that young trees surround adult trees in the same way as adults surround adults. Therefore, these results imply low densities of “recruits” in the vicinity of their conspecific potential parents. This lack of recruits near conspecific adults might be consistent with Janzen-Connell effects at small scales (Wright 2002) and establishment limitation due to abiotic or biotic constraints (Luo et al. 2011). The Janzen-Connell hypothesis describes host specific pests and or pathogens reduce recruitment near conspecific adults (Janzen 1970; Connell 1971). On the other hand, seeds that get far from parent trees have more chance to survive and arrive in favorable sites (Hood et al. 2004). Additional support for the Janzen-Connell hypothesis is provided by the fact that g21-g22< 0 for all life stage associations, except those in D. sylvatica implying that young individuals are clumped independently and not closely to their conspecific adults and highlighting recruitment limitation near conspecific adults.

In conclusion, our major objectives were to explore the spatial patterns and associations of dominant tree species and how they are influenced by heterogeneous environmental conditions. Through spatial point-pattern analyses, the results clearly show the impacts of environmental heterogeneity on horizontal structure, and intra- and inter-specific interactions. Meanwhile, there are still many unanswered questions that may be solved if more information is integrated on the ecological characteristics of trees. Moreover, spatial pattern analysis at larger scales may exhibit more effects of environmental heterogeneity as suggested by Boyden et al.(2005).

Acknowledgement

This study was supported with funds from the Ministry of Education and Training of Vietnam. Permission to work and access to the study site was provided by the director of Babe National Park, Vietnam. Field work was conducted by Mr. Nghia, Mr. Nhuan and local people. Stephan Getzin was supported by the European Research Council (ERC) Advanced Grant “SpatioDiversity” (grant number 233066). We also thank Barbara Strauss for her helpful comments on the manuscript.

Augspurger CK. 1984. Seedling survival of tropical tree species - Interactions of dispersal distance, Light-gaps, and Pathogens. Ecology, 65(6): 1705-1712.

Barot S. 2004. Mechanisms promoting plant coexistence: can all the proposed processes be reconciled? Oikos, 106(1): 185-192.

Boyden S, Binkley D , Shepperd W. 2005. Spatial and temporal patterns in structure, regeneration, and mortality of an old-growth ponderosa pine forest in the Colorado Front Range. Forest Ecology and Management 219(1): 43-55.

Bruno JF, Stachowicz JJ, Bertness MD. 2003. Inclusion of facilitation into ecological theory. Trends in Ecology & Evolution, 18(3): 119-125.

Bunyavejchewin S, Lafrankie JV, Baker PJ, Kanzaki M, Ashton PS, Yamakura T. 2003. Spatial distribution patterns of the dominant canopy dipterocarp species in a seasonal dry evergreen forest in western Thailand. Forest Ecology and Management, 175(1-3): 87-101.

Callaway RM, Walker LR. 1997. Competition and facilitation: A synthetic approach to interactions in plant communities. Ecology, 78(7): 1958-1965.

Condit R, Ashton PS, Baker P, Bunyavejchewin S, Gunatilleke S, Gunatilleke N, Hubbell SP, Foster RB, Itoh A, LaFrankie JV, Lee HS, Losos E, Manokaran N, Sukumar R, Yamakura T. 2000. Spatial patterns in the distribution of tropical tree species. Science, 288(5470): 1414-1418.

Condit R, Hubbell SP, Foster RB. 1992. Recruitment near conspecific adults and the maintenance of tree and shrub diversity in a neotropical forest. American Naturalist, 140(2): 261-286.

Connell JH. 1971. On the role of natural enemies in preventing competitive exclusion in some marine animals and in rain forest trees. In: P. J. den Boer and G. Gradwell (eds), Dynamics of Populations. Pudoc, Wageningen, pp. 298-312.

Debski I, Burslem D, Palmiotto PA, Lafrankie JV, Lee HS, Manokaran N. 2002. Habitat preferences of Aporosa in two Malaysian forests: Implications for abundance and coexistence. Ecology, 83(7): 2005-2018.

Diggle PJ. 2003. Statistical Analysis of Spatial Point Patterns. London: Arnold (Hodder Headline Group).

Dixon PM. 2002. Ripley’s K function. In: Abdel H. El-Shaarawi and Walter W. Piegorsch (eds), Encyclopedia of Environmetrics. Chichester: John Wiley & Sons, pp.1796–1803

FIPI. 1996. Vietnam forest trees. Hanoi, Vietnam: Agricultural Pub. House.

Getzin S, Wiegand T, Wiegand K, He F. 2008. Heterogeneity influences spatial patterns and demographics in forest stands. Journal Of Ecology, 96(4): 807-820.

Goreaud F, Pelissier R. 2003. Avoiding misinterpretation of biotic interactions with the intertype K-12-function: population independence vs. random labelling hypotheses. Journal of Vegetation Science, 14(5): 681-692.

Gunatilleke CVS, Gunatilleke IAUN, Esufali S, Harms KE, Ashton PMS, Burslem DFRP, Ashton PS. 2006. Species-habitat associations in a Sri Lankan dipterocarp forest. Journal of Tropical Ecology, 22: 371-384.

Harms KE, Condit R, Hubbell SP, Foster RB. 2001. Habitat associations of trees and shrubs in a 50-ha neotropical forest plot. Journal of Ecology 89(6): 947-959.

Harms KE, Wright SJ, Calderon O, Hernandez A, Herre EA. 2000. Pervasive density-dependent recruitment enhances seedling diversity in a tropical forest. Nature, 404(6777): 493-495.

He FL, Legendre P, LaFrankie JV. 1997. Distribution patterns of tree species in a Malaysian tropical rain forest. Journal of Vegetation Science, 8(1): 105-114.

Hood LA, Swaine MD, Mason PA. 2004. The influence of spatial patterns of damping-off disease and arbuscular mycorrhizal colonization on tree seedling establishment in Ghanaian tropical forest soil. Journal of Ecology, 92(5): 816-823.

Hubbell SP. 1979. Tree dispersion, abundance, and diversity in a tropical dry forest. Science, 203(4387): 1299-1309.

Hubbell SP, Ahumada JA, Condit R, Foster RB. 2001. Local neighborhood effects on long-term survival of individual trees in a neotropical forest. Ecological Research 16(5): 859-875.

Illian J, Stoyan D, Stoyan H, Penttinen A. 2008. Statistical Analysis and Modelling of Spatial Point Patterns. Sussex: Wiley.

Janzen DH. 1970. Herbivores and the number of tree species in tropical forests. American Naturalist, 104(940): 501-528

Lan G, Getzin S, Wiegand T, Hu Y, Xie G, Zhu H, Cao M. 2012. Spatial Distribution and Interspecific Associations of Tree Species in a Tropical Seasonal Rain Forest of China. Plos One, 7(9).

Li H, Reynolds JF. 1995. On definition and quantification of heterogeneity. Oikos, 73(2): 280-284.

Luo ZR, Mi XC, Chen XR, Ye ZL, Ding BY. 2011. Density dependence is not very prevalent in a heterogeneous subtropical forest. Oikos, 121(8): 1239-1250.

Martinez I, Wiegand T, Gonzalez-Taboada F, Ramon Obeso J. 2010. Spatial associations among tree species in a temperate forest community in North-western Spain. Forest Ecology and Management, 260(4): 456-465.

McDonald RI, Peet RK, Urban DL. 2003. Spatial pattern of Quercus regeneration limitation and Acer rubrum invasion in a Piedmont forest. Journal of Vegetation Science, 14(3): 441-450.

North M, Chen JQ, Oakley B, Song B, Rudnicki M, Gray A, Innes J. 2004. Forest stand structure and pattern of old-growth western hemlock/Douglas-fir and mixed-conifer forests. Forest Science, 50(3): 299-311.

Peters HA. 2003. Neighbour-regulated mortality: the influence of positive and negative density dependence on tree populations in species-rich tropical forests. Ecology Letters, 6(8): 757-765.

Pizano C, Mangan SA, Herre EA, Eom A-H, Dalling JW. 2011. Above- and belowground interactions drive habitat segregation between two cryptic species of tropical trees. Ecology, 92(1): 47-56.

Rcfee. 2011. Forest ecological stratification in Vietnam. Hanoi.

Ripley BD. 1976. The Second-Order Analysis of Stationary Point Processes Journal of Applied Probability, 13(2): 255-266

Seidler TG, Plotkin JB. 2006. Seed dispersal and spatial pattern in tropical trees. Plos Biology, 4(11): 2132-2137.

Somanathan H, Borges RM. 2000. Influence of exploitation on population structure, spatial distribution and reproductive success of dioecious species in a fragmented cloud forest in India. Biological Conservation, 94(2): 243-256.

Stoyan D, Stoyan H. 1994. Fractals, random shapes, and point fields: Methods of geometrical statistics. Chichester: John Wiley & Sons.

Team RDC. 2010. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing.

Tilman D. 2004. Niche tradeoffs, neutrality, and community structure: A stochastic theory of resource competition, invasion, and community assembly. Proceedings of the National Academy of Sciences of the United States of America, 101(30): 10854-10861.

Uriarte M, Canham CD, Thompson J, Zimmerman JK. 2004a. A neighborhood analysis of tree growth and survival in a hurricane-driven tropical forest. Ecological Monographs, 74(4): 591-614.

Uriarte M, Condit R, Canham CD, Hubbell SP. 2004b. A spatially explicit model of sapling growth in a tropical forest: does the identity of neighbours matter? Journal of Ecology, 92(2): 348-360.

Wagner HH, Fortin MJ. 2005. Spatial analysis of landscapes: Concepts and statistics. Ecology, 86(8): 1975-1987.

Wang XP, Jin XB, Sun CY. 1986. Burretiodendron hsienmu Chun &How: Its Ecology and Its Protection. Arnoldia, 45(4): 46-51.

Wang XG, Wiegand T, Hao ZQ, Li BH, Ye J, Lin F. 2010. Species associations in an old-growth temperate forest in north-eastern China. Journal of Ecology, 98(3): 674-686.

Webb CO, Peart DR. 2000. Habitat associations of trees and seedlings in a Bornean rain forest. Journal of Ecology, 88(3): 464-478.

Wiegand T, Gunatilleke S, Gunatilleke N. 2007. Species associations in a heterogeneous Sri lankan dipterocarp forest. American Naturalist, 170(4): E77-E95.

Wiegand T, Huth A, Getzin S, Wang X, Hao Z, Gunatilleke CVS, Gunatilleke IAUN. 2012. Testing the independent species' arrangement assertion made by theories of stochastic geometry of biodiversity. Proceedings of the Royal Society B-Biological Sciences, 279(1741): 3312-3320.

Wiegand T, Moloney KA. 2004. Rings, circles, and null-models for point pattern analysis in ecology. Oikos, 104(2): 209-229.

Wiens JA. 2000. Ecological heterogeneity: an ontogeny of concepts and approaches. In: M. J. Hutchings, E. A. John and A. J. A. Stewart (eds), The ecological consequences of environmental heterogeneity. Oxford Blackwell Science, pp.9-32.

Wright SJ. 2002. Plant diversity in tropical forests: a review of mechanisms of species coexistence. Oecologia, 130(1): 1-14.

Yamada T, Tomita A, Itoh A, Yamakura T, Ohkubo T, Kanzaki M, Tan S, Ashton PS. 2006. Habitat associations of Sterculiaceae trees in a Bornean rain forest plot. Journal of Vegetation Science, 17(5): 559-566.

Zhang Z-H, Hu G, Zhu J-D, Luo D-H, Ni J. 2010. Spatial patterns and interspecific associations of dominant tree species in two old-growth karst forests, SW China. Ecological Research, 25(6): 1151-1160.

Zhang ZH, Hu G, Zhu JD, Ni J. 2013. Aggregated spatial distributions of species in a subtropical karst forest, southwestern China. Journal of Plant Ecology, 6(2): 131-140.

Zhu Y, Mi XC, Ren HB, Ma KP. 2009. Density dependence is prevalent in a heterogeneous subtropical forest. Oikos, 119(1): 109-119.

Appendix 1: Inter-specific association: (+) attraction, (0) independence and (-) repulsion

Appendix 2: Intra-specific association between life stages: (+) attraction, (0) independence and (-) repulsion