基于SIFT的图像匹配算法的研究
2014-04-18谢志文黄小雪
许 睿,谢志文,黄小雪,龚 琼,万 航
(1. 桂林电子科技大学, 广西 桂林 541004;2. 桂林市环保局,广西 桂林 541002)
基于SIFT的图像匹配算法的研究
许 睿1,谢志文1,黄小雪2,龚 琼1,万 航1
(1. 桂林电子科技大学, 广西 桂林 541004;2. 桂林市环保局,广西 桂林 541002)
SIFT特征匹配算法具有很强的匹配优势,当图像发生角度改变、位置改变、视觉角度变换、光照强度变化、仿射演变情况下,仍能正确匹配。通过实验验证了算法的匹配优势。
图像匹配; 特征提取;SIFT算法

图像匹配是视觉技术的基础,许多学者对图像之间的匹配技术进行了大量研究和改进,提出了多种算法,SIFT特征匹配算法是比较成功的算法之一[1]。
1 SIFT特征向量生成
SIFT算法是特征提取和图像识别技术[2,3],主要包括两个过程,一是特征生成,一是特征向量匹配。
1.1 尺度空间上的极值检测
将图像I(x,y)的尺度假设为L(x,y,σ),由高斯函数G(x,y,σ)和图像I(x,y)卷积生成:
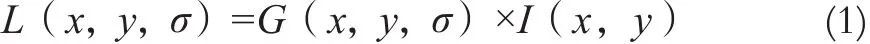
想要在尺度空间找到固定的关键点坐标,应在高斯差分函数与图像卷积生成的空间D(x,y,σ)中检测极值点:
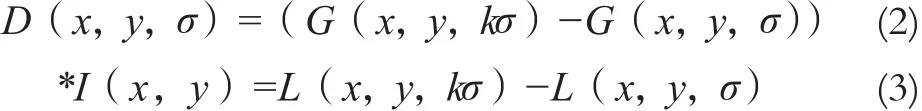
其中相邻两个尺度由一个常数k分开。有两个理由:一是节约计算时间,计算D时只要计算相邻尺度函数的差值。二是D的属性与尺度归一化的拉普拉斯高斯函数σ2∇2G 很相似[4]。
因为拉普拉斯函数与尺度不相关,所以高斯差分函数也与尺度不相关。对于所有尺度而言,k是一个常量,所以使用D不会影响极值的选择。当k 远离1 时,误差会越来越大。但实际上,k跟极值的选取无关。利用金字塔得到高斯差分图像,如图1。
金子塔被分为多层。从第一层开始,对第一幅图像连续用高斯函数卷积,生成许多逐渐平滑的图像。在这一层中,相近的高斯图像差分得到高斯差分图像。等这组结束后,从中抽取一幅图像a进行降采样,获得图像b,面积变是a的1/4,并让b作为下一层的初始图像,重复第一层的过程。选择a的原则是获得a所要的尺度空间S的参数σ是原始S的2 倍。假设k = 21/t,在t个尺度中找寻极大值或极小值,平均每层要有t+3 幅图像,得到t+2 幅高斯差分图像。经验值为1.6×21/3和3,说明k取值21/3。
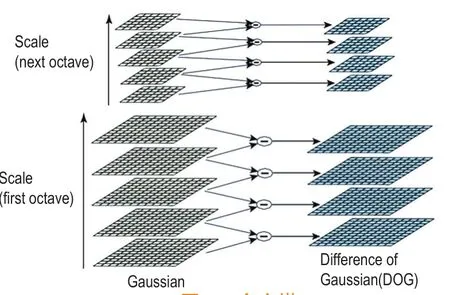
图1 金字塔
1.2 关键点的定位
对上面得到的极值点进行挑选,除掉不稳定的点。不稳定点包括边缘点和低对比度的点。对于某一个尺度上求取的极值点,采用一个3维的2次函数求其在原图像上的位置,并去除低对比度的点。首先在某极值点A对D(x,y,σ)进行泰勒展开:

其中,X(x,y,σ)T是到点A 的偏移量。对式(4)求X 的偏导数并令偏导为零,得:

如果x大于0.5,说明这个极值点和另一个采样点离得更近,采用插值法求得极值点位置的估计值。同时,可以利用D(x^) 去除低对比度的点。将式(5)代入式(4)得:
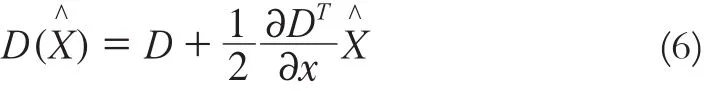

设α是较大的特征值,β是较小的特征值,由矩阵性质知:
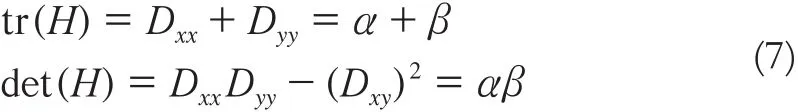
一般情况下这里的行列式不会是负值,如果出现负值,即两个主曲率不同号,不将其视为极值点。设r=α/β,得:

(r +1)2 / r 是递增函数。要得到主曲率的比值r,判断上式左边是否在开关值以下即可。开关值一般取值r=10。
1.3 为关键点标定方向
为关键点随便赋一个方向,定义的关键点描述子是相对于这个方向的,因而可以实现匹配时图像的旋转不相关性[6]。 为了证明跟尺度没有关系,筛选与这个尺度最毗邻的高斯平滑图像L,对于L上的每个点L(x, y),计算梯度和方向:

划分一个相邻区域,让关键点作为中心,使用在这个范围内的点的梯度得到某个未知方向直方图。此图的X坐标表示梯度朝向,共有36 项,每一项表示10°;Y轴表示梯度范围,对于划归到X轴的所有点,把梯度取值作加法运算,其和作为Y轴取值。Y轴取值最大的方向是关键点的主要方向。Y轴的取值大于主要方向Y轴取值的过半以上,也认为是关键点方向。特征点有多个方向,也就是有多个关键点。为了使稳定性更好,可以对关键点邻域的梯度进行高斯加权[7]。
1.4 提取特征点描述符
为了保证旋转不变,需将坐标轴翻转为重要点的方向。以特征点为中心,选取8×8邻域,把特征点与取样点相向方向高斯加权,然后划入包含8个方向的直方图,得到2×2×8即32维特征描述子,如图2。

图2 32维特征描述子
一个小正方形表示了特征点附近尺度范围的某个像素点,箭头方向表示像素梯度朝向,箭头长度表示梯度取值。在4×4范围内计算8个方向的梯度方向直方图,如图3 。描绘每个梯度方向的累加可形成一个种子点。每一个描述符都包含一个位于关键点邻域的4个直方图数组,每个直方图有8方向的梯度方向。因此SIFT的特征向量有128维。
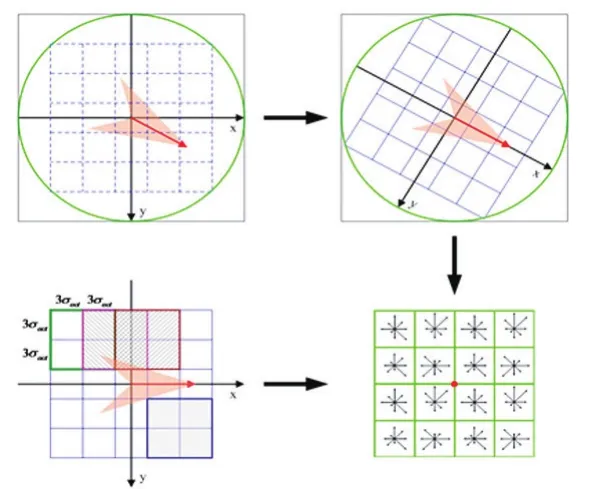
图3 梯度方向直方图
2 实验及分析
采用VS2010实现整个实验过程。图4是原始图像,图5是图4旋转90°后所得图像。用SIFT程序实验,得图6。从实验结果可以看出,SIFT算法对处理图像旋转具有很好的效果。图7是图4放大两倍的结果,把图4和图7进行匹配得到图8。通过实验可以看出,图像大小并不影响匹配的效果。

图4 原始图像

图5 旋转90°后图像

图6 SIFT匹配结果1

图7 放大2倍后图像

图8 SIFT匹配结果2
[1] Lowe D G. Object Recognition from Local Scale –Invariant Features[C]. 7th Int Conf Computer Vision, 1999
[2] Brown M, Lowe D G. Invariant Features from Interest Point Groups[C]. British Machine Vision Conference,Cardiff,Wales, 2002
[3] Lowe D G. Distinctive Image Features from Scale –Invariant Keypoints[J]. Int J Computer Vision, 2004,60(2):91-110
[4] 吴锐航. 基于SIFT特征的图像检索[J].计算机应用研究,2008(2):478-481
[5] 高成,董长虹,郭磊,等,MATLAB图像处理与应用[M].北京:国防工业出版社,2007
[6] 张正友,马颂德.计算机视觉——计算理论与算法基础[M].北京:科学出版社,2003
[7] 王永明, 王贵锦. 图像局部不变性特征与描述[M]. 北京: 国防工业出版社, 2010
P237.3
B
1672-4623(2014)04-0072-03
10.11709/j.issn.1672-4623.2014.04.025
许睿,副教授,主要从事遥感与图像识别研究。
2013-08-26。
项目来源:国家自然科学基金资助项目(31200326);国家科技支撑计划资助项目(2011BAK12B04);中国博士后基金资助项目(20110491727);广西科学研究和技术开发资助项目(GKG 1140002-2-4)。
