节气在公历日期的哪一天

□ 萧耐园

节气在公历日期的哪一天

□ 萧耐园

二十四节气的确立

二十四节气作为我国古代的独特创造，是我国传统历法的重要组成部分。早在西周和春秋时期，通过圭表测影，已能确定冬至、夏至、春分和秋分的时刻。战国时期，又增加了立春、立夏、立秋和立冬4个节气。在西汉初年的典籍《淮南子·天文训》中，二十四节气已经完备。汉武帝太初元年（公元前104年）颁行了《太初历》，历史上首次把二十四节气完整地订入了历法，这是一个重大的进步。

我国的传统历法，包括现在仍在颁行的农历，是一种阴阳历。阴历以反映月亮盈亏变化周期的朔望月为时间长度的基准。1朔望月的平均长度为29.5306日。阴历中历月分为大月和小月两种，大月30日，小月29日，1历年12个月的长度为354日（平年354日，闰年355日）。这与反映四季变化周期的回归年（365.24219日）相差明显。因此纯粹的阴历与四季变迁的步调不匹配。甲骨文显示我国至迟在殷商时代就采用置闰的办法，即通过在若干年内加入1个闰月，使这一年（闰年）的历年长度成为384（或383）日，于是历年的平均长度在若干年内接近于1回归年，以克服这一缺陷，这就使阴历与阳历结合起来了。也就是说，阴阳历中加入闰月是“阳”的成分。即便这样，由于具体的历年长度毕竟与回归年不符，因而历法上的月和日与农业生产的节令无法形成确切的对应关系。为了克服这个问题，中国古代独创了二十四节气。

二十四节气是我国传统历法中又一种“阳”的成分。最初的二十四节气是把1回归年的日数等分成24份，即约15.22日为1份，从冬至日起每隔15.22日设定1个节气。这样设置节气的方式称为“平气”。但到唐代天文学家一行编算《大衍历》时，考虑到太阳在黄道上周年视运动的不均匀性，他将黄道等分为24份，在天球上自西向东黄经每增加15°为1个节气。这样设置节气的方式称为“定气”。由于冬至前后太阳移行快而夏至前后太阳移行慢，前者1个节气只有14天多，后者1个节气近16天，所以各个节气之间的时间间隔是不等长的。此后这种划分二十四节气的方法一直沿用下来了。二十四节气与公历的日期有基本固定的对应性。在我国的普通天文学教科书上，通常会列出二十四节气表，表中列出各个节气的太阳黄经和公历对应日期，如右表。

节气日期存在漂移现象

有读者发现本刊有些文章所载夏至的日期不一致，投信本刊询问。事实上夏至在2011年是6月22日，可是到了2012年、2013年和2014年都是6月21日，而到了2015年夏至又是6月22日。从表中可见，每个节气确实可以出现在两个日期。不止于此，实际上每个节气还都可能出现在3个日期。例如夏至在2056年以后会出现在6月20日。笔者承蒙中国科学院紫金山天文台历算室惠予提供400年间的节气日期和时刻数据，由此数据首先可见，随着时间递增节气向前漂移（指节气从大日期向小日期转化）；其次，多数节气的漂移是从闰年开始，而小寒、大寒、立春和雨水的漂移却从闰后1年开始；再次，节气的漂移会连续地出现在2年甚至3年之内。为什么会出现这些情况呢？

要解决这些问题，先要了解现行公历的编制。

现行公历由罗马教皇格里高利十三世主持制订，颁行于1582年。公历规定平年历年长度为365日，每4年，即当公历年份能被4整除时，置1闰，加1日，闰年长度为366日，闰日加于2月末。又规定若世纪年如1700、1800、1900、2100……等不能被400除尽的不作为闰年，而只有1600、2000等能被400整除的，才为闰年。这样一来，400年里只加了97个闰日，使历年平均长度为365.2425日。这与回归年的差为0.0003日/年，即每3300年才有1日的误差。所以说现行公历能很好地反映节气的变迁。那么为什么还会出现上述问题呢？这就与现行公历的具体编排有关了。

上述历年平均长度与回归年的高精度符合是在400年内取平均实现的，但就具体每一年来说历年只能取整数，平年365日，闰年366日。因此1回归年的长度，即节气的变迁周期比平年1历年要长，显然同一节气在相邻两历年里的日期可能不固定，即逐年向前漂移，可是一逢闰年，历日会有1整日的“跳跃”，于是交节日期相对地移动1日，从而阻止了交节日期的无限制向前漂移。问题归结为弄清节气漂移和历日跳跃的相互关系。

节气日期的计算

紫金山天文台编算的《中国天文年历》有专门的节气表，节气所在时刻精确到时分，对于民用，这个精度足够了。这是对于视太阳的位置给出的。笔者根据公历的具体编排总结出两个公式，列于下面。用这两个公式可以由已知某年的交节日期计算其他年份同一节气的日期。当然不可能对视太阳来算，而是一种平均结果，所得结果对于实际值会有最多达三十来分钟（相当于太阳黄经1.2′）的偏差。但是对于回答上面的问题，公式的计算结果是有效的。

式中TN为年份数为N的年内某节气的交节时刻，以日（d）、时（h）、分（m）表示；TM为选定为初始年的M年内同一节气的交节时刻；5.8126h是1回归年对于365日的多余部分，即0.24219×24h= 5.8126h；INT（X）表示对于数值X取小于等于其代数值的整数，例如INT（1）=1，INT（1.1）=1，INT（－1）=－1, INT（－1.1）=－2等，这一项在于考虑到每4年即逢闰年，历法的1日跳跃，使得节气所在日期相对来说提前了1日。之所以两个公式略有差别，就因为闰日加在2月底，对于在1、2月份的4个节气上述跳跃的影响实际上发生在下一年的年初。原则上M可以任意选取，但最好选一个闰年，这样两个公式在形式上较为规整，也便于下面的讨论。

笔者取M=2000，T2000取紫台历算室提供的相应数据（公式中21d9h48m即为2000年的夏至交节时刻），用上列两式作计算，以说明夏至的问题，用（1）式：

我们的计算符合实际情况。由此可以看出正是由于历年长度与回归年长度每年有5.8126h的差值，且差值随着时间的递增而累积。虽然每4年加进的闰日在一定程度上减缓了累积的进程，但漂移还是继续向前。

从以上夏至日的算例可见，节气的漂移确实发生了。事实上，若节气的漂移量不超过24h，就只跨两日。如果超过了24h，就能跨3日了。那么一般情况下漂移量多大？什么情况下会漂移到下一日？漂移量有没有上限？各在什么时间范围内能确定某一个节气取1日、2日或3日？这是下面探讨的问题。

以（1）式为例说明之，把这一式加以变形（注意M恒取闰年）：

上式右端第二项（下表中以II表示）中的11.25m=（6h－5.8126h）×60，其中的6h对应于第三项花扩号内的前一项，II的值连续减小，当N－M=32、64、96和128时，II的值依次为－6h、－12h、－18h和－24h；第三项（下表中以III表示）中花扩号内是余数，不论N－M＞0或＜0，取值为0（闰年）、+0.25（闰后1年）、+0.5（闰后2年）和+0.75（闰后3年），相应地III间断性地取值0h、+6h、+12h和+18h。我们看到TM的数值是可以改变的，遍及从0h到24h，我们又说过TM可以任意选取。所以，不失一般性，我们可以取任何一日（设为K+1）的TM=K+1d0h0m加以讨论，用（3）式计算，计算结果列于下表。下表中，若TN≥0，节气日期不漂移；若0＞TN≥－24，节气日期向前漂移1日；若TN＜－24，节气日期向前漂移2日。

线（时）段序号N－M I I I I I T N 漂移情况对应下图线段0年 0h0m0h0h0m1均在K + 1日 K + 1日的密虚线1 .－0 1 1 6 5 4 9 2－0 2 3 1 2 1 1 3 7 3－0 3 4 1 8 1 7 2 6 4－0 4 5 0 －0 4 5 漂移到K日 K日的点虚线5－0 5 6 6 5 4 回到K + 1日 K + 1日的密虚线6～3 1 依此类推，得1段K + 1日的密虚线和与之相应的 K日的点虚线3 2 －6 0 0h－6 0 均漂移到K日 K日的疏虚线3 3 －6 1 1 6 －0 1 1 3 4 －6 2 3 1 2 5 3 7 回到K + 1日 K + 1日的疏虚线3 5 －6 3 4 1 8 1 1 2 6 3 6～6 3 依此类推，得1段K + 1日的疏虚线和与之相应的 K日的疏虚线6 4 －1 2 0 0h－1 2 0均漂移到K日 K日的密虚线9 7 －1 8 1 1 6 －1 2 1 1 9 8 －1 8 2 3 1 2 －6 2 3 9 9 －1 8 3 4 1 8 －0 3 4 1 0 0～1 2 7 依此类推，K + 1日的线段终止，得1段K日的实线1 2 8 －2 4 0 0h－2 4 0均在K日 K日的密虚线6 5 －1 2 1 1 6 －6 1 1 6 6 －1 2 2 3 1 2 －0 2 3 6 7 －1 2 3 4 1 8 5 2 6 回到K + 1日 K + 1日的点虚线6 8～9 5 依此类推，得1段K + 1日的点虚线和与之相应的 K日的密虚线9 6 －1 8 0 0h－1 8 0均漂移到K日 K日的实线2 . 3 . 4 . 5 . 6 . 7 . 1 2 9 －2 4 1 1 6 －1 8 1 1 1 3 0 －2 4 2 3 1 2 －1 2 2 3 1 3 1 －2 4 3 4 1 8 －6 3 4 1 3 2 －2 4 5 6 0h－2 4 5 6 漂移到K－1日 K－1日的点虚线1 3 3～1 5 9 依此类推，得1段K日的密虚线和与之相应的 K－1日的点虚线1 6 0 －3 0 0 0h－3 0 0 漂移到K－1日 K－1日的疏虚线1 6 1 －3 0 1 1 6 －2 4 1 1 1 6 2 －3 0 2 3 1 2 －1 8 2 3 回到K日 K日的疏虚线1 6 3 －3 0 3 4 1 8 －1 2 3 4 1 6 4～1 9 1 依此类推，得1段K日的疏虚线和与之相应的 K－1日的疏虚线1 9 2 －3 6 0 0h－3 6 0漂移到K－1日 K－1日的密虚线1 9 3 －3 6 1 1 6 －3 0 1 1 1 9 4 －3 6 2 3 1 2 －2 4 2 3 1 9 5 －3 6 3 4 1 8 －1 8 3 4 回到K日 K日的点虚线1 9 6～2 2 3 依此类推，得1段K日的点虚线和与之相应的 K－1日的密虚线

（此图为后期重新绘制，仅供参考）

从上表的算例可见，如果中间没有间断，当一个节气从K+1日经K日漂移到K－1日的期间，可以对于每一日画出1条直线，其中对于K日描画出1条长达224年的直线。这条直线由7个线段组成，每一段32年，顺次为红点虚线、蓝疏虚线、绿密虚线、橙色实线、绿密虚线、蓝疏虚线、红点虚线。其中前3段各与K+1日的相应线段相对，后3段与K－1日的相应线段相对（见上图）。

上图表示上表的计算结果，从上到下画出K+1日、K日和K－1日的3条直线。纵坐标为3个日期，横坐标表示N－M，单位是年，图中还标出了各线段的序号。对于K+1日和K－1日的2条直线又分别向前（N－M=－1～－32）和向后（NM=224～255）各多推算32年（推算过程和结果未列于表中），分别标为－1段和第8段。

对于任何一个节气，必有一个32年的时间范围（第4时段），期间仅取1个确定的日期。但只要把这个范围仅向前（或仅向后）扩展1年，它的漂移就达到2个日期了；如果同时向前或向后各扩展1年，它的漂移就达到3个日期了。由此可见，想要把1个节气确定为1个日期，并无多大意义。尤其是想要找到1个时间范围，让所有节气在这同一范围内都确定为各自的1个日期，简直不可能。漂移为2个日期的时间范围就大得多了。从图可见，在从－1时段到第4时段或从第4时段到第8时段的5个时段范围，即160年内都符合这个条件。同样，只要时间范围仅仅扩展1年，漂移就达到3个日期了。漂移为3个日期的时间范围就更大了，不再多加讨论。如果着眼于1个世纪来考察，在100年内，任何一个节气不可能只有1个日期，而有2个日期或3个日期的可能性都是存在的。如果要计算这两种情况各自出现的概率，也不太难，但是没有实际意义，也就不去损伤脑细胞了。

事实上，上述理想状态下的直线并不存在，根据这条直线讨论的漂移情况往往不符合实际，因为直线存在间断。这种间断来自于现行公历规定的400年里有3个世纪年不置闰。在世纪之交的年份，当符合这一规定时，交节日期相对于历法日期比置闰时多加1日，于是向前的漂移中断。紫台历算室又提供了上述数据中1950年至2100年150年间的各节气日期图，列于文后。从这些图明显可见，绝大多数节气在这150年内可以出现在3个日期。同时，图还显示代表节气所在日期的每条直线包含了4种线条：红点虚线、蓝疏虚线、绿密虚线和橙色实线。而且上下相邻的两条直线间一条线中的红点虚线与另一条的绿密虚线相对，一条线中的蓝疏虚线与另一条的蓝疏虚线相对，每条线中的橙色实线的上下都没有线相对。我们的计算结果是与真实情况相符的。

我们选图中的谷雨节气为例来看，与紫台历算室提供的实算数据比较，M相当于1884年，T1884=20d0h36m（K+1=20）。按照理想状况，我们将得到19日（K日）的1条持续的直线，而实际上这条直线在1900年上移了1日。又由于2000年是闰年，结果我们得到了1条20日在200年里没有间断的直线，可是在2100年再度中断。实际情况是，有的节气在1世纪内有2个日期，而另一些有3个日期。看来想要设定一个区间，让所有节气都“有2个日期”或都“有3个日期”也无法做到。此外，也许这种间断能增加“有2个日期”的概率，例如，在20世纪，1900年有间断，“有2个日期”的节气有14个（占58%），而在20世纪，只有11个（占46%）。

民众应用的节气，通常根据日历所载或媒体通告，究其来源在紫台历算室，自然有确定的日期。本文只是根据自己的理解对节气日期的不确定进行了一番分析，希望通过此文能与有相同兴趣的读者朋友交流沟通。

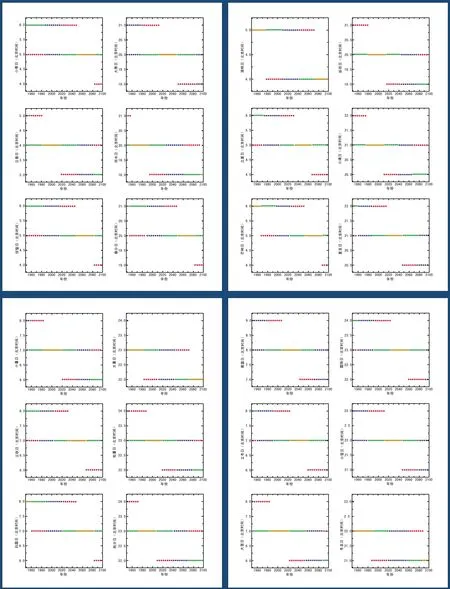
1950年至2100年各节气日期图

（责任编辑 张恩红）