一种二元高超声速进气道起动特性的尺度效应研究

凌 岗，李祝飞，肖丰收，姜宏亮，刘坤伟，高文智，杨基明

（1.中国科学技术大学近代力学系，合肥 230027；2.中国空气动力研究与发展中心，四川绵阳 621000）

0 引 言

进气道作为吸气式高超声速飞行器的主要部件，通过捕获和压缩空气，为发动机燃烧室提供所需来流条件，其起动性能的好坏将直接影响推进系统能否正常工作。因此进气道的起动性能是判断高超声速进气道设计优劣的一个关键指标［1］。

进气道“起动”状态，一般来说是指当进气道内部的流动现象没有改变进气道流量捕获特性时，进气道是起动的［2］。引起进气道不起动的主要因素有：来流马赫数过低，捕获的流量难于全部通过喉道；激波边界层等复杂干扰引起分离，造成流动壅塞；反压过高，超出隔离段承受能力等等［3］。目前的研究对后两者关注比较多。

在传统的风洞实验中，通常实验模拟首先保证的是来流马赫数相等，模型几何相似，而在其他方面则可能会根据具体情况不得不适当放宽相似要求。例如受风洞尺寸的限制，实验模型相对飞行器来说大多会有一定比例的缩小。在高超声速进气道相关研究中，为了充分体现内外流耦合的特征，实验模型往往需要采用机体与进气道的一体化设计，这将进一步使得进气道部分的尺寸受限而采用较大幅度的缩比模型。值得注意的是，对于不同尺度的进气道模型，由于一体化耦合的复杂性，雷诺数、气流热力参数甚至壁温等条件变化时，其流场结构、边界层转捩位置、分离区大小等都会有一定程度的差别，从而影响进气道的起动能力。由此可见，在高超声速进气道起动实验中，尺度效应是不容忽视的问题。

尺度效应引起的差异，已引起国内外学者的关注。在理论上，国内外有不少研究指出了传统风洞实验模型设计缩尺比例由风洞尺寸决定的方法的不足，并提出了通过CFD对地面实验结果进行修正，以得到与真实飞行条件下更为接近的数据［4－6］。Pulsonetti和Stalker在研究尺度对超燃冲压发动机的影响时指出，不同尺度模型边界层厚度的变化会对进气道工作状态产生一定的影响［7］。国防科学技术大学的金亮等研究了模型缩比尺度对飞行器整体性能的影响，指出内流道摩阻系数不同会导致全尺寸模型与缩比模型阻力系数的不同［8］。南航的刘凯礼研究了不同尺度对进气道动态迎角特性的影响，指出随着进气道尺度增加，放大后的进气道动态迎角的影响也随之增加［9］。在这些研究中，作者们大多关注的是进气道缩尺效应对气动特性的影响，而对于进气道起动性能的研究尚未见到相关报道。

本文针对进气道不同缩尺模型，开展自起动马赫数的数值模拟，考察了这些缩尺模型之间起动性能的差异；同时对这种差异进行分析，期望找出其影响机理。在数值模拟的基础上，选择合适的模型进行必要的实验考核和探讨。

1 计算与实验方法

为便于研究，减少过多复杂因素的干扰，选取了一种结构简单的二元进气道模型。图1（a）为采用的高超声速二元混压式进气道模型示意图。外压段采用两级压缩，唇口为尖前缘设计，进气道基准模型选用的内收缩比为1.53，通过前后移动唇口位置可以改变进气道内收缩比。此构型在本课题组前期研究中有一定的基础，数据较为丰富，有利于结果的比较。基准进气道构型的具体尺寸参照相关文献［10］。为提高计算效率，对三维计算域进行了半模等简化，如图1（b）所示。图1（c）为实验中所采用模型的照片。

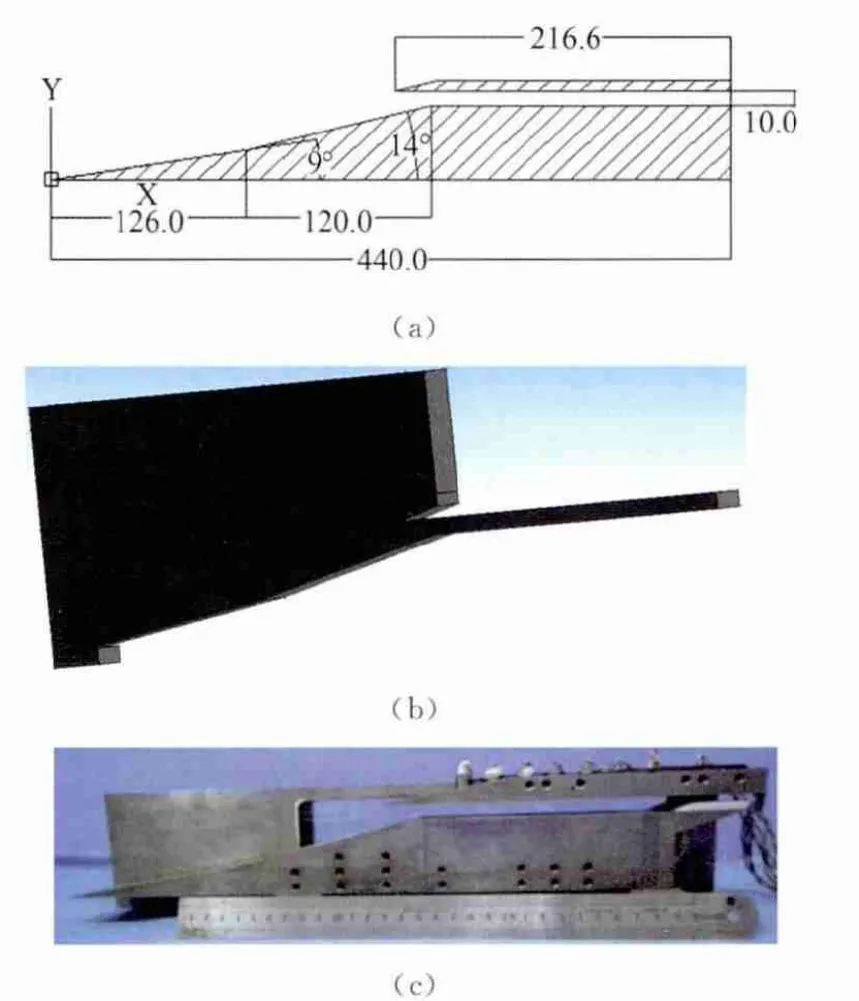
图1 二元进气道计算与实验模型Fig.1 Diagram of 2Dhypersonic inlet and Computational domain

计算采用Fluent商用软件进行N－S方程数值求解，湍流模型选择S－A模型，通量格式采用AUSM格式。边界条件采用压力远场条件、压强出口条件和等温无滑移固壁，粘性系数采用Sutherland公式计算。计算以低马赫数（如M∞＝3）得到进气道不起动流场，然后以上一步的收敛解作为初场，逐步增加来流马赫数进行续算，直至进气道起动，所对应的马赫数即为自起动马赫数［11］。为便于实验验证，本文采用激波风洞实验中M∞＝5.9条件相同的动压和总温配置得到各来流马赫数下的来流条件。在这种配置方法下，来流单位雷诺数Re1，∞约为5.1×106m－1。计算中涉及到变雷诺数的问题都是以此来流和构型尺寸为基准条件（即表1中的1∶1尺度）进行的。

计算主要从两个方面进行了考核，表1给出了数值模拟的主要内容。算例1主要对不同缩比模型自起动马赫数进行了模拟，以考核尺度效应对进气道自起动马赫数的影响。考虑到便于比较以及之后匹配雷诺数的方便，除基准模型外，计算中主要选择了1∶2和1∶4模型进行数值模拟，另外，为增大考核范围，还选择了1∶10的模型进行对比。算例2主要考核雷诺数的影响，具体来说是通过提高1∶2模型的来流单位雷诺数使其和基准条件下1∶1模型的雷诺数相等来考核其起动能力。

表1 典型算例参数设置Table 1 Typical cases in the numerical simulation

计算中对1∶1模型分别给出了310万和186万左右两种网格形式，近壁面处网格采用等比加密，壁面第一层网格高度5μm，计算得到两种网格计算自起动马赫数分别为4.6和4.7，变化很小。为减少计算量，采用网格较少的模型。另外，在来流M∞＝5.5时对比数值纹影与实验结果，发现二者的流场结构与实验结果也吻合得较好（这在后文的实验部分有所说明），表明计算结果具有较好的可信度。

2 结果讨论与分析

2.1 不同缩尺模型的自起动马赫数

在进气道起动研究中，一般认为分离激波位于进气道入口之后，没有亚声速溢流，即进气道内部的流动现象没有改变进气道流量捕获特性时，认为进气道处于起动状态。图2给出了1∶1模型不同马赫数下的对称面马赫数分布和壁面极限流线图。从图中可以看出，在M∞＝3时，进气道入口存在比较大的分离，分离激波在进气道入口前，流道有明显的壅塞，大量气流从进气道唇口外部溢出，进气道处于不起动状态。

在来流马赫数增加到4.5和4.6时，分离激波位置虽然位于进气道进口内侧，但由于流动的三维性，壁面极限流线图上看到，实际上在侧板和唇口交界处，仍有大量的气流溢出，说明在这两个来流马赫数条件下，进气道依然是不起动的。然而，当继续增加来流马赫数到4.7时，流场结构却出现了显著的变化：对称面马赫数分布图上看出入口处分离激波消失，进气道内部形成畅通的超声速流道，壁面极限流线图上也没有明显的溢流。表明在这个来流马赫数下，进气道已经处于起动状态。由此判断，1∶1模型自起动马赫数为4.7。同样，对其他三种缩比模型自起动情况也进行了数值模拟。表2给出了各缩比模型自起动马赫数比较情况。可以看出，随着模型尺度的减小，进气道自起动马赫数有明显的增加，特别是在模型缩小到1∶10时，进气道很难实现自起动，自起动马赫数已经增加到了Mselfstart＝7.6。

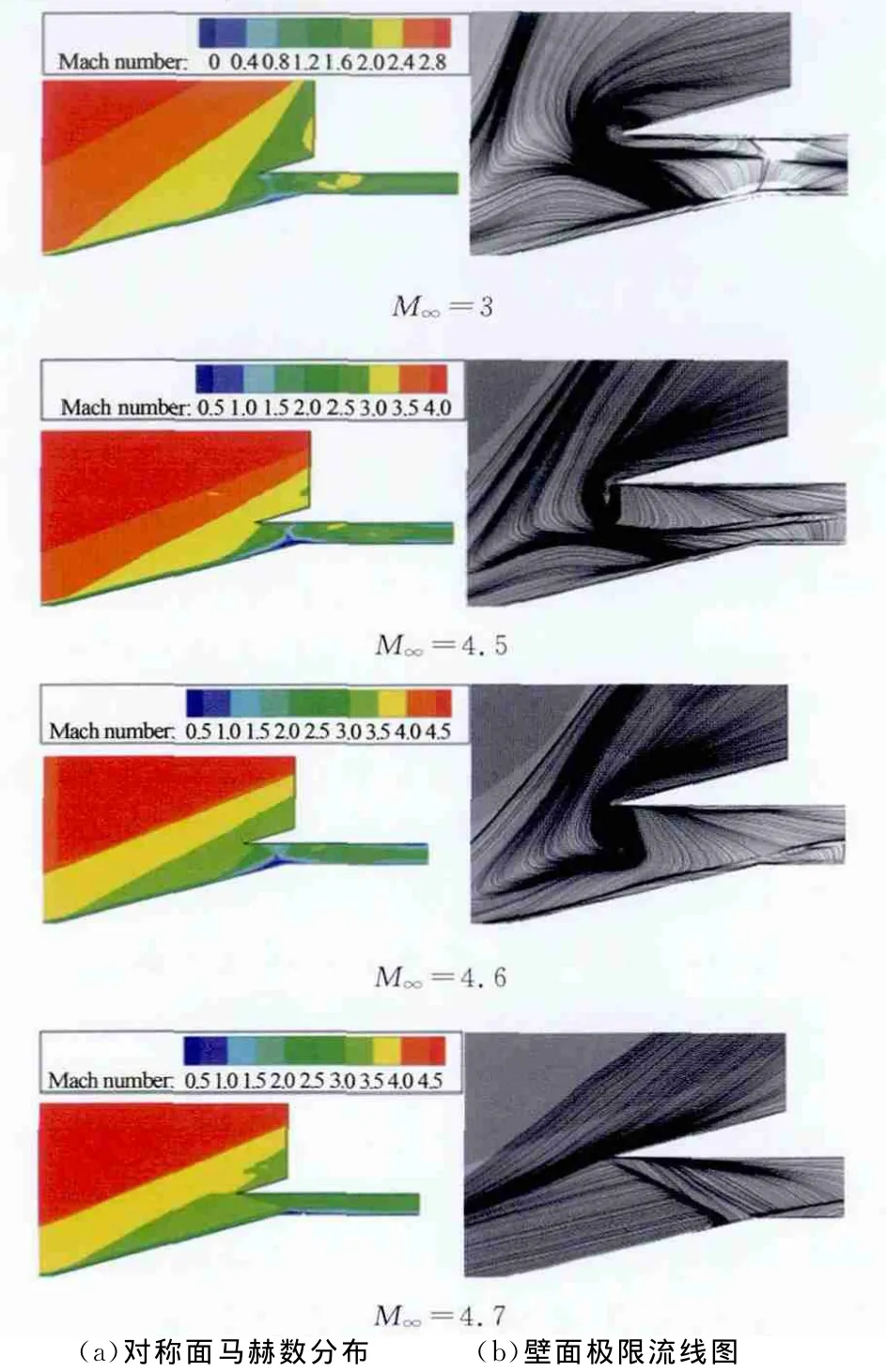
图2 1∶1模型不同来流马赫数条件下流场Fig.2 The flow field in different Mach numbers of 1∶1model

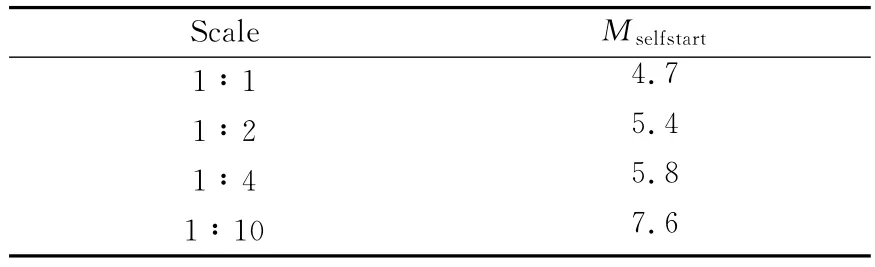
表2 各缩比模型对应的自起动马赫数Table 2 Self－starting Mach number of different models

为分析导致不同缩尺模型自起动马赫数不同的原因，对不同缩尺模型流场结构进行了对比。为了突出尺寸的影响，这里固定单位雷诺数，并统一选择M∞＝4.5的流场来比较各模型不起动状态下的流场结构。图3分别给出了各缩比模型在M∞＝4.5时入口附近对称面的马赫数分布。从图中可以直观看到，随着模型尺度的减小，进气道入口处流动分离区随之增大，分离激波逐渐被推向上游。

在相同单位雷诺数条件下，不同缩尺模型的雷诺数是不同的，而分离区的大小和雷诺数有很大的关系。因此有必要对雷诺数进行重点考察。

图3 各模型M∞＝4.5对称面马赫数分布Fig.3 The Mach number contour in the symmetry plane of M∞＝4.5

2.2 雷诺数对进气道起动性能的影响

为研究雷诺数的影响，对1∶2模型和1∶1模型雷诺数进行匹配。将1∶2模型单位雷诺数提高1倍，使其雷诺数和基准条件下1∶1模型雷诺数相等（主要通过改变来流密度来改变单位雷诺数）。图4给出了提高单位雷诺数后1∶2模型在M∞＝4.5和M∞＝4.6条件下的流场。从图中可以看出，M∞＝4.5时进气道还处于不起动状态，而在M∞＝4.6时，进气道实现了起动，说明在此来流条件下，1∶2模型自起动马赫数为4.6，远低于原来（即雷诺数减半）的Mselfstart＝5.4，与1∶1模型的自起动马赫数非常接近。

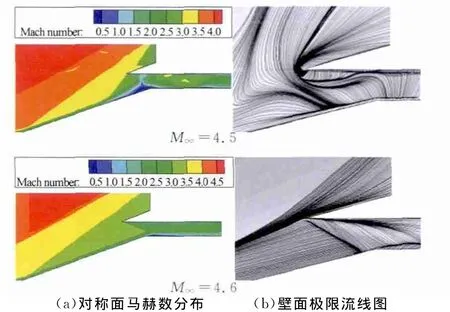
图4 1∶2模型提高雷诺数后不同来流马赫数条件下流场Fig.4 The flow field in different Mach number of 1∶2model after increasing Reynolds number

通过以上对比发现，在雷诺数提高以后，模型自起动马赫数有所降低，即自起动能力有所增强。并且在相同雷诺数条件下，不同尺度模型的自起动马赫数基本能保持一致。由此可以推断，雷诺数确实是引起不同缩尺模型自起动性能不同的主要因素。

2.3 相关实验结果讨论

实验在中国科学技术大学的激波风洞中进行，风洞可提供马赫数5.5和5.9两种典型的来流条件［12］，考核内收缩比1.53和1.77的二元高超声速进气道模型的起动性能。M5.5来流总压为0.78MPa，总温为710K，单位雷诺数约为4.6×106m－1，而M5.9在基准单位雷诺数5.1×106m－1下的来流总压为1.27MPa，总温为810K。其中，内收缩比1.77的进气道模型由收缩比1.53模型唇口前移10mm得到（参见图1（a））。采用在进气道出口附近事先设置轻质堵块的方法，检测进气道的自起动能力［12］。

图5为内收缩比1.53进气道模型在M∞＝5.5来流条件下自起动过程的纹影照片（t′对应于激波风洞实验段流场开始建立的时刻）。轻质堵块的堵塞作用使得进气道在风洞运行前期很快出现不起动，而当轻质堵块被吹出流道后，外压缩面上的分离激波退回进气道入口，并被喉道吞入，进气道能够重新建立稳定的起动流场。表明内收缩比1.53的进气道在M∞＝5.5来流条件下，具有自起动能力。前文的数值模拟已经指出，该进气道的最小自起动马赫数在4.7左右，实验来流马赫数高于其自起动马赫数，进气道能够自起动。

图6给出了内收缩比1.53的1∶1模型在M∞＝5.5来流条件下的数值纹影，对比实验结果可以看出，数值模拟的波系结构与实验结果吻合较好。

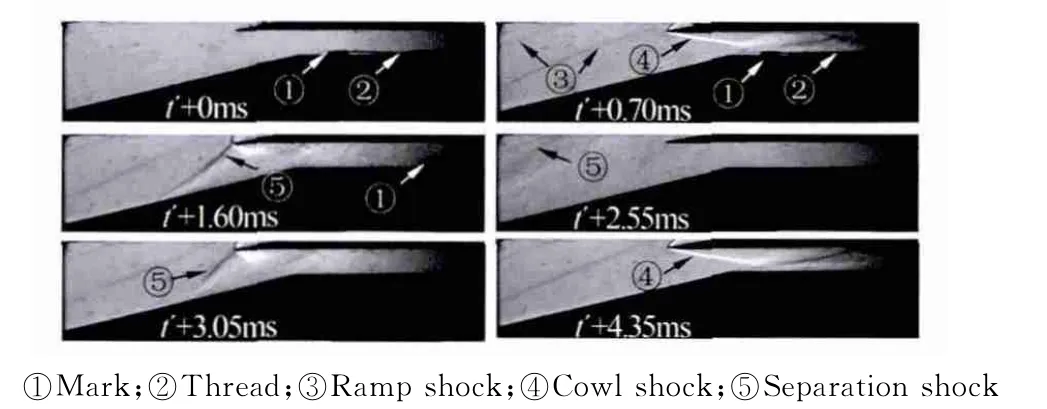
图5 M∞＝5.5内收缩比1.53进气道自起动纹影Fig.5 Schlieren photographs of self－starting of the ICR＝1.53inlet at M∞＝5.5

图6 M∞＝5.5内收缩比1.53进气道自起动数值纹影Fig.6 Numerical schlieren of self－starting of the ICR＝1.53inlet at M∞＝5.5

考虑到激波风洞所提供的来流马赫数有限，为了进一步丰富实验考核内容，将模型的内收缩比增大至1.77。

数值模拟表明（见图7（a）），内收缩比1.77进气道的最小自起动马赫数为5.8。图7（b）给出了内收缩比1.77进气道模型在M∞＝5.5来流条件下，初始设置堵块时的纹影照片序列。在堵块被吹出流道后，进气道入口始终被大范围的流动分离区所占据，进气道不能完成自起动过程。

图7 M∞＝5.5内收缩比1.77进气道不能自起动Fig.7 Self－unstarting of the ICR＝1.77inlet at M∞＝5.5

M∞＝5.9来流条件下，实验结果如图8所示，当流道恢复通畅后，进气道能够建立起动的流场结构，表明内收缩比1.77的进气道在M∞＝5.9时，具有自起动能力。内收缩比1.77进气道在M∞＝5.5和M∞＝5.9两种来流条件下的起动性能实验结果与数值模拟的预报结果相符合，在一定程度上支持了数值模拟的合理性。

图8 M∞＝5.9内收缩比1.77进气道自起动纹影Fig.8 Schlieren photograph of self－starting of the ICR＝1.77inlet at M∞＝5.9

另外，为研究雷诺数的影响，在M∞＝5.9来流条件下，对1.77内收缩比模型在不同单位雷诺数下进行了试验。图9分别给出了单位雷诺数降低到原来的1／2和1／3的实验纹影。在单位雷诺数降为1／2时，在堵块被吹出流道后，进气道入口始终有大范围的流动分离区，进气道不能实现自起动，然而有意思的是，当单位雷诺数继续下降到1／3时，当堵块被吹出，流道恢复畅通后，进气道出人意料地建立了起动的流场结构！这就意味着在更低的雷诺数下进气道反而能够起动。这与前文所得到的低雷诺数下不容易起动的结论完全相反。

图9 低雷诺数下实验结果Fig.9 The experimental results under lower Reynolds number condition

3 来流流态对进气道起动性能的影响

为了分析上述低雷诺数下进气道异常起动的原因，这里对来流流态进行一定的数值模拟探讨。考虑到模型尺度很小的低雷诺数流动时，流动很可能为层流状态。已有的研究一般认为层流更容易引起流动分离，不利于进气道的起动。但这一概念与本文的上述实验结果已经出现了难以自圆其说的矛盾。为弄清楚其中的原因，对进气道不同来流流态下的自起动性能进行了数值模拟。为便于比较，数值模拟条件与实验条件一致，进气道内收缩比为1.77，缩尺比例为1∶1。

图10和11分别给出了湍流S－A模拟和层流模型在M∞＝5.9时的数值模拟结果。

从图10中不难看出，在湍流状态时，进气道入口气流呈壅塞状态，壁面极限流线图上也有明显的溢流，显然此时进气道处于不起动状态；而在层流状态下，可以看到，尽管进气道入口有较厚的边界层存在，但其主体部分已经形成畅通的超声速通道，壁面极限流线图上也没有明显的溢流，进气道呈现出“起动”的特征。

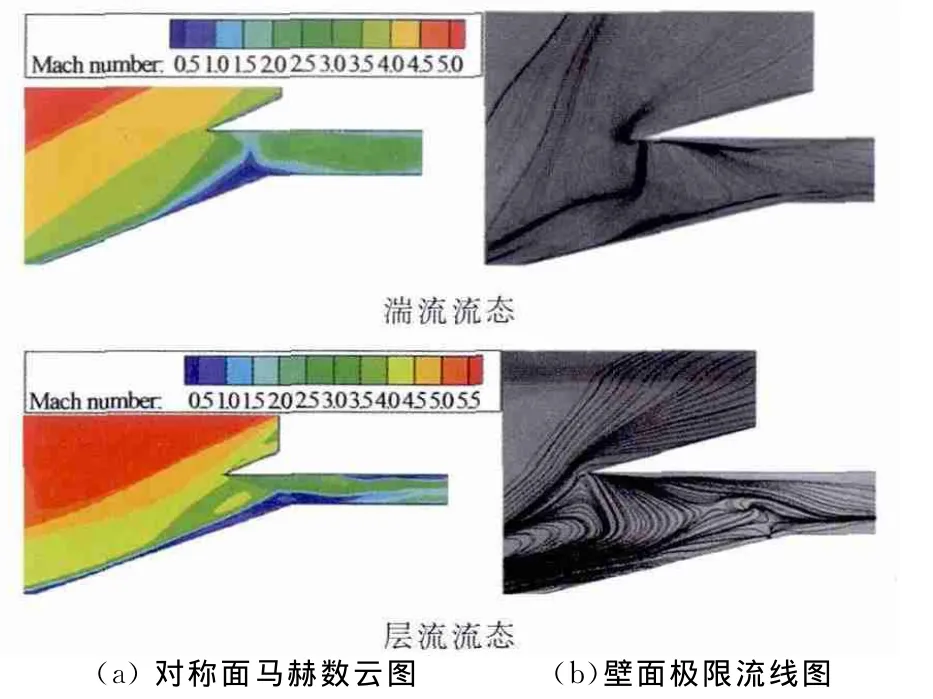
图10 不同流态下数值流场Fig.10 The flow field of CFD in different flow model

为了更加清晰地和实验结果进行对比，图11给出了层流状态下的数值纹影结果。对比图9（b）的实验结果可以发现，层流状态下的数值纹影和实验照片的波系结构基本一致。特别是在图9（b）的波系与下壁面的反射作用区域有一定的外移，表明该处存在相对较厚的局部低速流动区域；而图11中对应的区域也存在着较为明显的亚声速低速流区，数值计算结果和实验结果吻合较好。

图11 层流状态下数值纹影结果Fig.11 Numerical schlieren in laminar flow condition

这就是说，数值模拟结果可以得到低雷诺数下进气道反而能“起动”的结果，而层流流态则在该“起动”过程中起着关键的作用。因此，通过实验和数值模拟结果综合考虑，作者对进气道在低雷诺数下反而呈现起动状态的倾向性解释是，在低雷诺数下，来流偏向于层流流态，使进气道呈现出一种“起动”状态。当然，这种“起动”是否属于真正意义上的起动，还有待于更深入的探讨，探究其具体影响机理的工作也正在开展。

4 结 论

对进气道在不同缩尺情况下的自起动性能进行了比较和分析，并开展了相关的实验观测，主要得到以下结论：

（1）在相同来流单位雷诺数下，不同缩尺模型在相同来流条件下自起动马赫数会有差异，随着模型尺度的减小，其自起动马赫数升高；

（2）雷诺数是影响进气道起动性能的重要因素，不同缩比模型在相同雷诺数下其自起动马赫数基本保持一致；

（3）在模型缩比严重，雷诺数过于偏低时，实验还观察到进气道的异常起动现象，对于其具体的形成机制还有待于进一步研究。

［1］ 范晓樯.高超声速进气道的设计、计算与实验研究［D］.长沙：国防科学技术大学，2006.Fan Xiaoqiang.The design of the hypersonic inlet calculation and experimental research［D］.Changsha：National University of Defense Technology，2006.

［2］ Van Wie D M，Kwork F T，Walsh R F.Starting characteristics of supersonic inlets［C］.In 32nd ASME SAE，and ASEE，Joint Propulsion Conference and Exhibit.AIAA 1996－2914，1996.

［3］ David M Van.Wie.Scramjet inlet［M］.New York：AIAA，2000.

［4］ 陈谟.如何使用CFD来确定风洞实验模型的缩尺比例［J］.宇航学报，2007，28（3）：594－597.Chen Mo.How to determine the scale ratio of wind tunnel test models by CFD［J］.Journal of Astronautics，2007，28（3）：594－597.

［5］ Weinberg S，Laganelli A，Martellucci A，et al.A plan for coupling wind tunnel testing with CFD techniques［C］.15thAerodynamics Testing Conference，1988，10.2514／6.1988－1996.

［6］ Boppe C.Future requirements of wind tunnels for CFD code verification［C］.14th Aerodynamic Testing Conference，1986，10.2514／6.1986－753.

［7］ Pulsonetti M V，Stalker R.A study of scramjet scaling［R］.AIAA 1996－4533.

［8］ 金亮，柳军，罗世彬，等.数值模拟模型尺度与来流条件对实验数据的影响［J］.空气动力学学报，2010：00258－1825.Jin Liang，Liu Jun，Luo Shibin，et al.Numerical study on the influence of model scale and inflow conditions in wind tunnel experiment［J］.Acta Aerodynamica Sinica，2010：0258－1825.

［9］ 刘凯礼.高超声速进气道动／稳态迎角特性研究［D］.南京：南京航空航天大学，2011.Liu Kaili.Research on aerodynamic characteristics of hypersonic inlets with dynamic／steady angle－of－attack［D］.Nanjin：Nanjing University of Aeronautics and Astronautics，2011.

［10］李祝飞，高文智，李鹏，等.二元高超声速进气道激波振荡特性实验［J］.推进技术，2012，33（05）：676－682.Li Zhufei，Gao Wenzhi，Li Peng，et al.Experimental investigation on the shock wave oscillation behaviors in a two－dimensional hypersonic inlet flow［J］.Journal of Propulsion Technology，2012，33（05）：676－682.

［11］游进，夏智勋，王登攀，等.高超声速进气道再起动特性及其影响因素数值模拟［J］.固体火箭技术，2011，34（02）：161－166.You Jin，Xia Zhixun，Wang Dengpan，et al.Numerical study on influencing factors of restarting characteristics for a hypersonic inlet［J］.Journal of Solid Rocket Technology，2011，34（02）：161－166.

［12］李祝飞，高文智，李鹏，等.一种进气道自起动特性检测方法［J］.实验流体力学，2013，27（4）：14－18.Li Zhufei，Gao Wenzhi，Li Peng，et al.A test method for inlet self－starting ability detection［J］.Journal of Experiments in Fluid Mechanics，2013，27（4）：14－18.