微纳米尺度流动实验研究的问题与进展

李战华，郑 旭

（中国科学院力学研究所非线性力学国家重点实验室，北京 100190）

1 微纳米流动研究的尺度范围和测量仪器

1.1 微纳流动的尺度范围

微纳米流动的尺度范围从1mm～1nm，跨越了从宏观尺度到分子尺度的6个数量级。在这个范围内，实验流体力学面临哪些物理问题呢？首先，宏观流体力学方程组的连续性假设的适用性要考虑；其次，宏观流体力学常用的无滑移边界条件由滑移边界条件替代的问题。微纳流动的最大特点是流体被“限制”在“狭小”空间中流动。表、界面作用（如静电力、范德华力等）的距离一般小于微米尺度，在宏观尺度下可以忽略，而在微纳米流动中可能起主导作用。

微纳米尺度下流体连续性假设适用性问题，已经从实验角度验证了，目前认为微米以上尺度管道仍符合经典流体力学理论［1］（见本文第2节）。但纳米尺度内（＜1μm），特别是10nm～1nm范围，实验验证正在进行。从理论上分析［2］，N－S方程采用的连续性假设是基于所研究的长度和时间尺度与“分子”动力学尺度之间的分离。要求水动力学时间尺度τq远大于微观液体分子运动的时间尺度τσ（τσ～10－12s＝1ps），要求受限空间尺度w 远大于液体粘性长度尺度lc（～1nm）。分子动力学模拟从理论上预测了连续性假设有可能适用至1nm［2－3］。

目前研究表明光滑亲水表面的滑移长度小于20nm，相对于特征尺度在毫米量级以上的宏观流动，这种滑移现象的确可以不考虑。但对微纳尺度流动，边界滑移的影响难以忽略。Navier 1823年提出的滑移边界条件｜（u为滑移速度，u为流场wslip速度，b为滑移长度），仅是唯象公式，其中滑移长度b、滑移速度uslip的理论描述与定量测量仍吸引人们在研究（见本文第3节）。

在微纳米尺度流动中，表界面作用对流动有重要的影响，特别对电解质溶液［1］。以往在电化学中采用的一些特征尺度如：双电层厚度λD、Dukhin长度lDu等将引入水动力学流场分析（见图1）。双电层厚度λD描述了电解质溶液在带电表面形成的电荷密度沿法向的分布，量级约为1～100nm。λD仅描述了溶液电荷的影响，而当管道宽度h＜5μm电驱动流动应该考虑表面电荷的影响［2］。Dukhin长度lDu描述了壁面电荷面密度Σ与溶液电荷密度ρS之比，即lDu＝／ρs。lDu量级约为1nm～1μm。相应的Dukhin数为lDu与h之比，即Du＝lDu／h。

图1 与微纳流动有关的特征长度［2］Fig.1 The typical dimensions in micro／nano flows

在微纳流动中，描述流动的方程组除了采用N－S方程以外，离子输运N－P方程、电荷分布Poisson－Boltzmann方程等也被引入耦合求解。当然从第一原理出发的非连续描述方法也成为理论分析的手段，读者可参考文献［1］。总之，微纳米尺度下的流动现象，涉及从连续流动到分子运动，必将诱发一些新的实验分析方法和手段。

1.2 微纳流动测量的主要仪器及方法

宏观尺度速度场测量采用PIV技术，适用流场特征尺度大于1mm，定位精度在100nm～1μm范围，示踪粒子尺寸100nm～10μm。为了测量微纳米尺度的流动，需要采用微／纳尺度粒子图像测速系统Micro／Nano PIV、测量界面力的SFA／AFM以及探测微量电流的pA电流计等实验仪器（见图2），其主要特点分别为：

·MicroPIV［4］测量的长度范围为1μm～1mm，定位精度大于100nm，示踪粒子直径范围为100～500nm，测速范围为1μm／s～10mm／s；

·NanoPIV［5］测量的长度范围为10nm～1μm，水平方向定位精度为10～100nm，垂直方向定位精度可达10nm量级。示踪粒子直径为10～200nm；

·SFA／AFM［6］测量的长度范围为1～100nm，定位精度小于1nm，测力范围0.01～100nN；

·pA电流计［7］一般用于测量特征长度在1～100nm的流道内的流向电流（streaming current）或离子电流（ionic current），测量精度一般在0.1pA。

上述几种测量仪器的主要原理与性能的介绍可参阅附录。

图2 微纳尺度流动主要测量仪器的特性示意图Fig.2 A schematic diagram of the major measurement devices in micro／nano flows and their characteristic parameters

根据本课题组在微纳尺度液体流动的实验积累，介绍以下几个方面的实验研究进展：（1）第2节为流体力学连续性假设适用性的实验验证，介绍了微米尺度管道流量测量实验，综述了一些文献获得的纳米尺度下的实验结果；（2）第3节为滑移边界条件，为了测量滑移长度，速度剖面测量成为关键，介绍了用Micro／Nano PIV测速的进展和问题；（3）第4节是关于微纳米粒子在无界流场和受限条件下的运动；（4）第5节以微纳复合管道为主，介绍微纳尺度流动下电场及浓度场等多物理场对流场的作用，出现浓度波的传播以及微尺度旋涡；（5）第6节简述微纳流动测量的需求及其发展的前景。

2 微纳尺度管流连续性假设适用性

2.1 问题提出

基于连续介质假设的Navier－Stokes方程如下

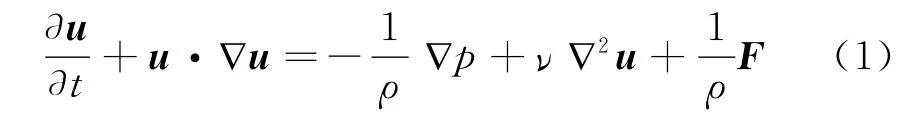
其中u是流场速度，p为压力，ρ和ν为流体密度和运动粘度，F为体积力。根据连续介质假设，只要流动特征尺度L远大于流体微元尺度δ，可采用N－S方程描述流动。但当流动特征尺度减小到微米甚至更小，N－S方程是否适用呢？直观的方法是测量微管道内流量Q与压力Δp的关系，与经典的管流公式预测值进行比较。

2.2 微尺度管流实验

依据Hagen－Poiseuille公式，直径为d的微管流量QTh应满足：

崔海航等［8］在0～30MPa高压下，测量了管径3～10μm的微管内多种简单液体的压力流量关系。他们发现，除水以外的简单液体：异丙醇、四氯化碳等在同样压力下实验流量Qexp偏离理论流量QTh。但考虑液体的粘性随压力改变μ＝μ（p），而引入粘压修正关系μapp＝μ0eαp后，微米尺度管道内流动仍然符合Hagen－Poiseuille公式，即C＊＝QTh／Qexp≈1。图3比较了2004年前不同实验室获得的微管道无量纲阻力系数随Re数的变化。可以看出，测量结果非常分散，而我们在Re＝0.5～100范围的实验结果（红色点标出）证明经典理论解仍然适用。

图3 微米尺度管道内流动无量纲阻力系数测量值随Re数分布［8－9］Fig.3 The variation of measured dimensionless friction coefficient with Re number in microtubes

由于Poiseuille公式中流量与直径的4次方成正比，管道直径测量的不确定度对测量结果影响很大。当微管直径大于10μm时，测量不确定度小于4.5%。但当微管直径小至3μm，测量不确定度高达13.4%。同时，需要施加的压力也随管径减小的4次方量级而增加。因此，在更小的尺度下用压力驱动进行类似实验，难度大大增加。

2.3 纳尺度流动的连续性假设适用性

当流道尺寸减小到百纳米量级甚至更小时，如果使用示踪法需要尽量减小示踪粒子尺寸，如使用5～10nm左右的粒子如量子点［10］。示踪方法受到粒子尺寸及光学分辨率的限制，因此这些年常用的测量方法仍是压力流量测量。为了降低驱动压力，管道一般用纳米阵列膜代替。2005年Majumder等［11］利用直径7nm的多壁碳纳米管膜（孔密度5×1010cm－2）在1个大气压下测量了液体流量，发现实验流速比Hagen－Poiseuille理论预测值高104量级，滑移长度高达3～68μm。2006年Holt等［12］制作了管径小于2nm的多壁和双壁碳纳米管阵列膜并用纳米粒子和TEM测试纳米管直径。他们分别测量了气体和液体流动的压力流量关系，发现滑移长度高达0.1～1μm。2008年Whitby等［13］使用直径约44nm的碳管阵列，10kPa压力驱动水、乙醇和癸烷等液体进行实验。他们发现流量增强40倍，对应的滑移长度约30～40nm。实验表明管径增加、流量增量减小，更加接近传统H－P压力流量公式。2011年我国学者Qin等［14］采用压力驱动水流过不同直径（0.98～1.10nm）的单根碳管，并通过电信号检测流量，发现流量增强可达100倍以上，对应滑移长度约5～50nm。2013年Kannam等［15］汇总了0.81～10nm直径的碳管流量测量结果（图4），发现滑移长度测量值分散在1nm～10μm约5个量级的范围内。我们分析上述测量结果相当分散的主要原因：（1）管径尺寸测量误差。用纳米管道阵列的孔隙率来估计流通截面，纳米管的重合、堵塞很难估计，还需要从管道加工及定量测量上改进；（2）流量采用电学检测方法时，由于纳流动特征尺度与双电层特征尺度相当，液体流动与壁面附近表面电荷输运耦合，测量结果不容易区分。因此纳尺度流动测量方法和结果还需做细致的分析和改进。

除了测量流量关系外，还有研究通过测量流体的传输系数校核连续性假设。比如测量动量传输系数（粘性系数）。Vinogradova［16］采用SFA测量疏水表面之间液膜的阻力时，发现液膜厚度在1～2nm范围内，水仍然保持其宏观尺度下的粘性系数。另外，关于热量传输系数（传热系数）［17］的实验也表明，基于连续介质假设的传输定律，包括傅里叶定律，在纳米尺度流动中仍然适用。从目前实验测量看出，连续性假设可以用到10nm以上的液体流动。实验方面正在向更小的尺度去努力。

图4 碳纳米管中滑移长度测量结果［15］Fig.4 The slip length measured results in carbon nanotubes

3 滑移长度与速度的测量

3.1 滑移边界条件

宏观流动中，边界条件一般采用无滑移假设。但微纳尺度流动中，当流动特征尺度逐渐接近滑移长度，需要考虑滑移边界。目前在液体微纳流动中，常采用Navier 1823年提出的边界滑移模型［18］：

图5给出了无滑移与滑移边界条件的图示，图5（a）为无滑移边界条件；图5（b）为滑移边界条件但假设流体与固壁间有一过渡层；图5（c）中假设流体与固壁接触界面有一滑移速度uslip。滑移速度uslip用公式（3）计算。滑移边界的实验研究首先是测量滑移长度b。

图5 Navier提出的边界滑移模型［19］Fig.5 The boundary slip model proposed by Navier

对于光滑表面，分子动力学（MD）模拟结果表征了亲疏水性接触角θ对滑移长度b的影响（见图6）［2］，提出滑移长度b与接触角θ满足如下关系：b∝（1＋cosθ）－2。对光滑亲水表面（θ＜90°），滑移长度b在0.1～1nm量级；即使对于光滑疏水表面，b也仅为1～10nm。目前常用测量滑移长度b的方法有两种：（1）MicroPIV／NanoPIV粒子示踪测量流场速度；（2）SFA／AFM表面力测量。但是实验测量结果有很大的分散性，在亲水表面（θ＜20°），滑移长度b本应该趋于0，但实验测量结果分散在几个纳米到几个微米之间（见图7）［20］。即使同样采用MicroPIV方法的测量结果也存在差异，因此郑旭等系统地进行了微尺度速度测量，下一节介绍他们的实验结果及解释。

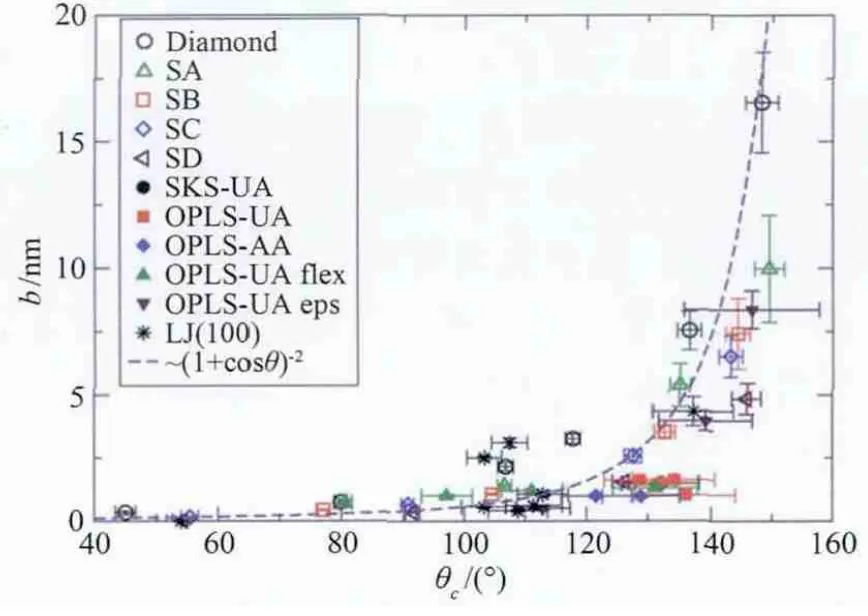
图6 MD模拟得到的滑移长度b随接触角θ变化的关系［2］Fig.6 The variation of the slip length b calculated by MD simulation with contact angle

图7 MicroPIV与SFA／AFM实验测量滑移长度在不同表面接触角下的分布［20］Fig.7 The variation of measured slip lengths both by MicroPIV and SFA／AFM with contact angle

3.2 MicroPIV速度剖面测量

郑旭等在本课题组的微纳米流动实验平台上采用直径200nm和50nm示踪粒子测量了PDMS矩形微流道玻璃底壁附近z≤3μm范围内的水平速度剖面［21］。结果表明在z＝0.25μm位置，用200nm粒子测量的速度值比理论值偏大达93.1%，而使用50nm粒子可使偏差下降50%。微管道近壁速度测量中，示踪粒子粒径影响显著。

依据Navier模型公式（3），根据垂向速度剖面估计滑移长度。使用50nm粒子时，滑移长度测量值约为b＝75±17nm。如图7所示MicroPIV测量的滑移长度比理论预测大。PIV或MicroPIV由示踪粒子图像计算速度场时有一假设，即所选窗口内粒子的浓度与速度是均匀分布。为了考察粒子浓度分布的均匀性，测量了近壁区纳米示踪粒子的浓度分布，发现粒子浓度呈现Boltzmann指数分布（见图8）［22］，

在z＋＞5（z＞250nm）范围粒子浓度呈均匀分布，而近壁区粒子浓度变稀。MicroPIV系统需要采用显微镜。一般显微镜的物镜焦平面厚度可由公式估计［4］。当使用100x／1. 35的物镜时，焦平面厚度约1.5μm。即使通过滤除非焦粒子等方法的处理，我们得到的焦平面厚度最薄约为0.5μm［21］。因此在近壁剪切流场中，示踪粒子分布不均匀，使得在焦平面厚度中求粒子平均速度时上层粒子权重加强，导致测量速度偏大（见图8）［20］。

图8 MicroPIV近壁测量时，剪切流场、粒子浓度非均匀分布和焦平面厚度共同导致测量速度偏大［20］Fig.8 The shear flow，the non－uniform particle concentration and the focal plane thickness result in larger measured velocity near wall in MicroPIV measurement

考虑到近壁粒子浓度分布的非均匀性对焦平面厚度内求粒子平均速度的影响，提出了测量速度的预测值［20］：

其中速度u（z）由三维速度无滑移理论解给出［23］，浓度分布c（z）由Boltzmann分布表示。那么，前述因素导致的测量速度偏差为：Δu（z）＝（z）－u（z），从测量速度uexp（z）中剔除此速度偏差后得到修正速度（z）为，

由修正后50nm粒子的测量速度分布，得到光滑亲水玻璃表面的滑移长度约17nm。MicroPIV的测量结果与SFA／AFM的测量结果基本一致，即对光滑亲水表面，滑移长度最大不会超过50nm（图9）。

3.3 NanoPIV近壁速度分布测量

为了更直接测量近壁区速度分布，进一步采用NanoPIV技术，用50～200nm示踪粒子测量亲水玻璃壁面附近100～600nm范围内的速度分布［24］。图10给出了NanoPIV测量结果与MicroPIV测量结果的比较，结果表明：NanoPIV测量的速度剖面比MicroPIV的测量结果在近壁区（z＜500nm）更符合理论速度预测值，采用小粒径示踪粒子或减小NanoPIV的渗透深度，可测到更贴近壁面的位置（z～100nm），但目前不同粒径的示踪粒子的测量速度在近壁（z＜100nm）处开始偏大。NanoPIV基于隐失波原理（参见附录（2）），壁面基准光强I0的选择对确定粒子垂向位置影响很大，一些有关的测量技术正在改进。根据Bocquet等人的理论分析［25］，考虑分子级别粗糙度影响的滑移长度b可以表示为：b～其中，k为波尔兹曼常数，T为热力学温B度，D为流体分子扩散系数，C⊥为表征分子级别粗糙度的几何因子，η为流体动力学粘度，ρ为流体密度，σ为分子间特征尺度，ε为液固分子间作用能。目前仍缺乏系统考虑表面粗糙度、液体成分及固体表面性质的滑移长度的实验测量。

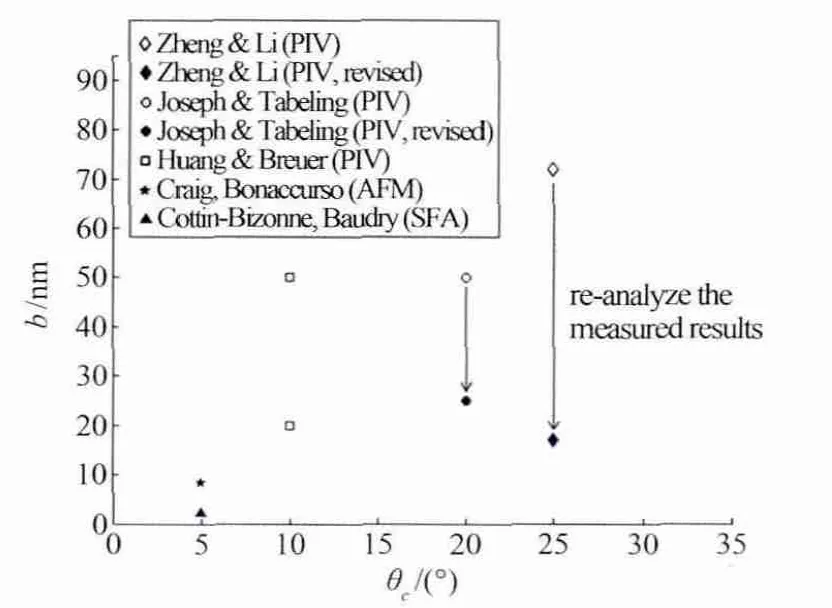
图9 修正后的MicroPIV测量滑移长度与SFA／AFM的测量结果基本一致［20］Fig.9 The revised MicroPIV measured slip lengths are in goodagreement with the SFA／AFM results

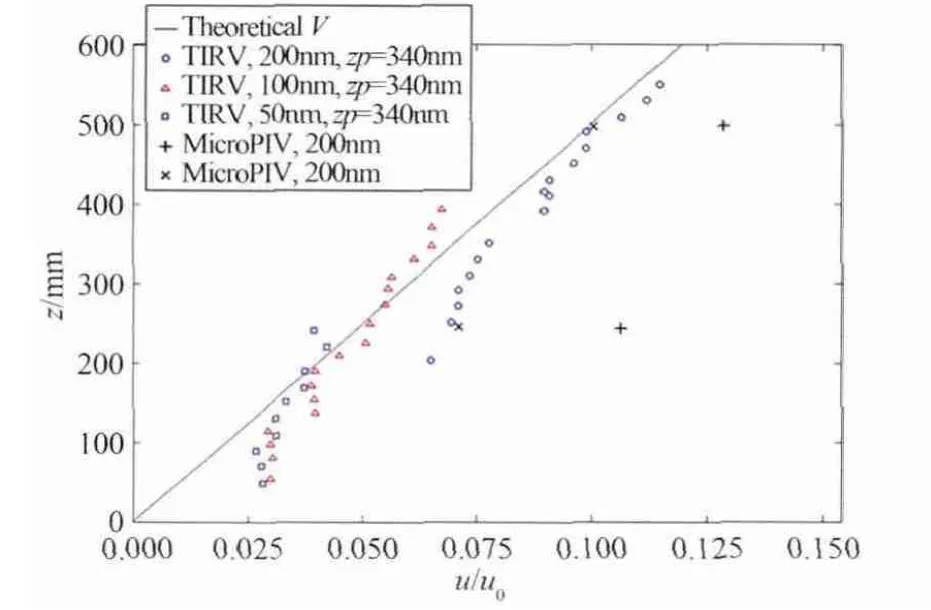
图10 MicroPIV、NanoPIV近壁速度测量结果与无滑移理论速度的比较［24］Fig.10 A comparison of the MicroPIV，NanoPIV near wall measured velocity profiles and the no－slip theoretical prediction

4 微纳米粒子运动的测量

微纳米尺度流动研究对象除了流体介质，还有细胞等颗粒状物质，因此对微纳尺度粒子运动的一般规律有必要进行研究。本节首先介绍无界流场中微纳米粒子运动，包括纳米粒子布朗运动和Janus微粒自扩散泳动实验研究，然后讲述受限条件下粒子运动。

4.1 纳米粒子布朗运动

在无界流体中粒子布朗运动的扩散系数可由Stokes－Einstein公式表示［26］：

且粒子布朗运动位移的概率密度满足高斯分布［26］：

我们分别测量了直径50～500nm粒子布朗运动扩散系数（见图11），发现500nm和200nm粒子的扩散系数D与Einstein公式预测相同，而50nm粒子的扩散系数D与理论值有差别。

如果用1／Dexp作纵坐标，我们发现无论直径50nm还是500nm，对应的粒径都变大了约8nm。对于500nm粒子，直径增加8nm并不影响扩散系数，而对50nm粒子的影响变得显著。实验用的聚苯乙烯粒子表面并不光滑，有可能是表面聚合物产生了水合层。因此对直径小于100nm的粒子，其布朗扩散系数要考虑粒子表面特性［27］。

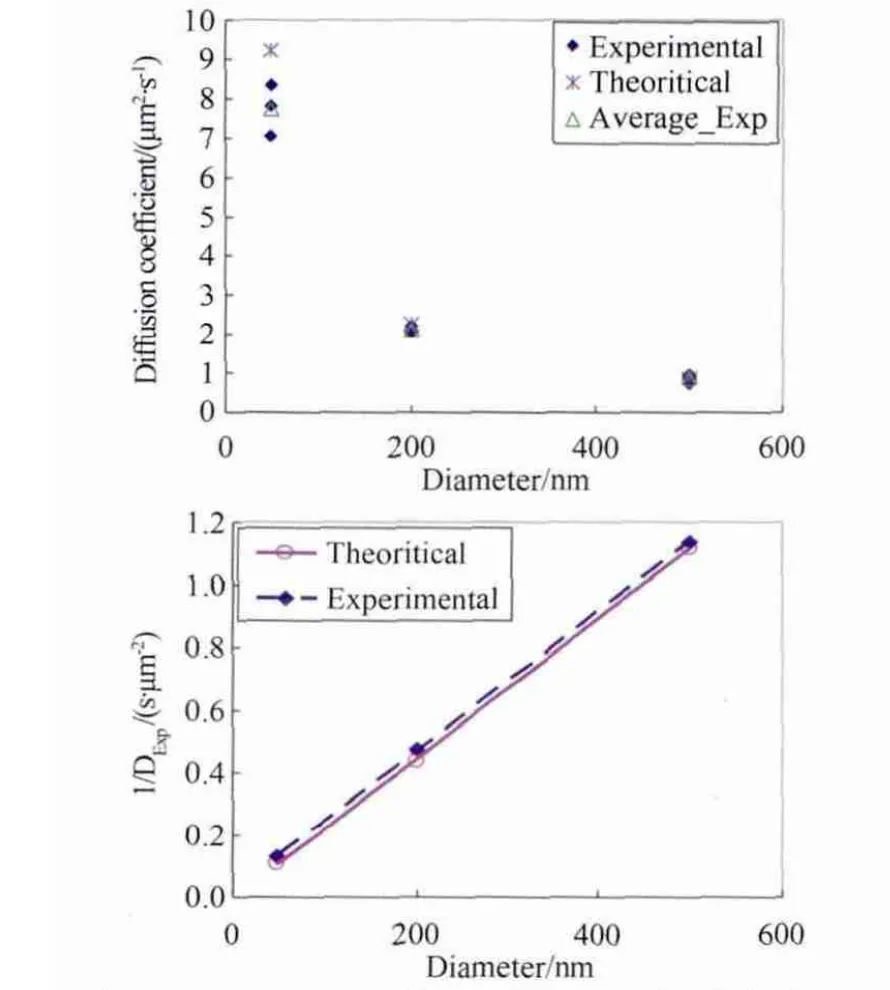
图11 Φ50～Φ500nm粒子布朗运动扩散系数测量［27］Fig.11 The measured results of the diffusion coefficient of Brownian motion ofΦ50～Φ500nm particles

4.2 Janus粒子运动

Janus粒子由化学性质不同的两个半球形成，其中一侧在溶液中会发生化学反应，在粒子周围形成浓度梯度。利用这种浓度梯度，Janus粒子产生自扩散泳动，成为把化学能转变为机械能的微尺度载体。实验测量发现，Janus粒子的有效扩散系数比同样直径均匀粒子布朗扩散系数大1～2数量级（见图12）［28］。最近实验研究发现，Janus粒子运动经历了简单布朗运动、强制推进和类布朗运动三个阶段，在中间阶段由于浓度梯度导致的推进作用使Janus粒子运动表现出明显的非高斯特性，如位移概率密度分布的双峰特性等（图13）［29］，而且粒子偏转角不是随机分布而是有取向性的。

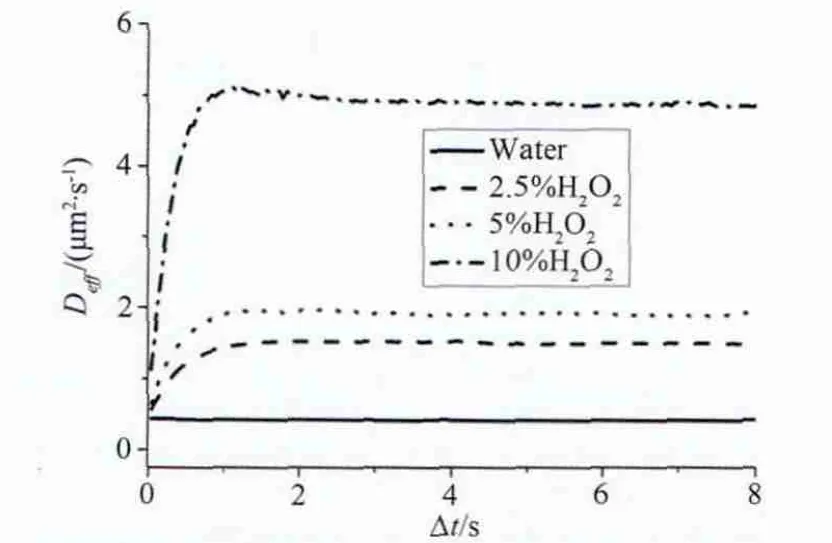
图12 Janus微球的有效扩散系数测量结果［28］Fig.12 The measured effective diffusion coefficient of Janus micro particles

图13 Janus微球位移概率密度双峰分布［29］Fig.13 The double－peaked structures of Janus micro particle’s displacement probability distribution

4.3 受限微纳米粒子运动

当微纳米粒子在近壁区或狭窄管道中运动，剪切流场、表面静电力、范德华力等在不同空间层次上对粒子运动均会产生影响。本节主要分析近壁静电力与Saffman力的作用，以及流向电势的影响。

当液固界面及粒子表面带电荷时，需要考虑静电作用。（9）式给出了壁面与粒子间的相互静电作用能［30］：

其中，ψw和ψp分别为壁面与粒子表面的表面电势，κ－1为德拜长度，ε为介电常数，q为单位电荷。一般用德拜长度表征静电作用的范围，其特征尺度约为1～100nm量级。

Saffman力是平行壁面运动的粒子在近壁剪切流作用下受到的侧向力。在近壁剪切流动较强时，Saffman力与静电力共同影响纳米粒子的运动。Saffman力表达式为［22］：

假设壁面电位势ψW为40～50mV，粒子表面电势ψB为10～20mV，壁面剪切率在2000～20000s－1范围，根据式（9）和（10）以计算静电力FE和Saffman力Fk在近壁区的分布（图14）。在z＋＜3.5范围，粒子受静电力影响为主，而在z＋≥3.5范围，Saffman力将起主导。显然在近壁200nm范围内，法向电场力影响为主，而远离壁面200nm后，剪切流场的水动力作用更为明显。同时，在Nernst－Planck方程中考虑Saffman侧向力FL，解得Saffman力与静电力共同作用下的粒子浓度分布，对Boltzmann分布做了修正［22］：

图14 静电力与Saffman力的比较［22］Fig.14 A comparison of the electrostatic force and the Saffman force

在更接近壁面的范围（1～10nm量级），还需要考虑纳米粒子受到壁面的范德华力作用［30］φVdW≈－其中A为Hamaker常数。范德华力沿壁面的法线方向影响粒子运动。

最后介绍流向电势的影响。在压力驱动电解质溶液流动中，如果管道特征尺度与壁面的双电层厚度可比，压力驱动会在管道两端储液池间形成流向电势（streaming potential）。流向电势可由下式计算［31］：

如果粒子表面带电，此电势将引起粒子电泳，其速度为：

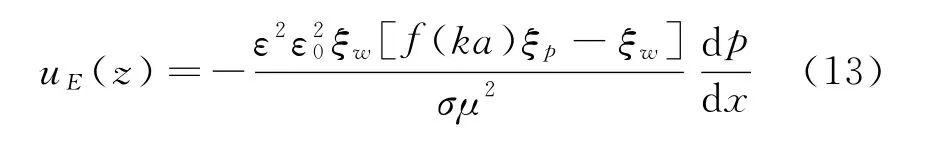
如果压力梯度dp／dx＝106Pa／m，粒子及壁面表面电荷ζp和ζw分别为50mV和20mV，粒子半径a＝100nm，电解质溶液电荷密度σ＝5×10－6S／m，则电泳速度可达到uE＝0.1mm／s量级。粒子的真实速度为流体速度与电泳速度的叠加。在第2.3节提到纳米通道流量实验可以通过测量电流估计，应该注意流向电位引起的粒子或离子的电泳运动。

5 微纳米复合管道的流动

微纳米复合管道作为微流控芯片组成部件之一具有样品富集、增强混合等功能，其管道内电解质溶液在电场驱动下产生电渗流。在微纳管道结合部，由于管道几何形状剧变，流场及电场梯度增强，导致溶液中离子富集或耗散。因此多物理场作用下在这类管道中产生许多水动力学现象。

5.1 多场耦合流动的波传播

三维微纳复合管道系统由两个PDMS微流道（横截面100μm×20μm，9mm长），与一个带纳米孔的PCTE薄膜6～8μm厚，纳米孔直径50nm，孔密度8×108cm－2）组成“三明治”型管道系统［32］（见图15）。

图15 微纳米复合管道系统［32］Fig.15 The hybrid micro／nano－channel system

在三维微纳复合管道系统上观察离子耗散富集现象［32］。如果在上侧微管道内注入缓冲液和荧光液，而下侧微管道仅注入缓冲液，当外加25V电压时，在上侧微管道中可以观察到在交叉区出现浓度耗散，然后此耗散区向两端储液池扩散。在另一侧微管道出现荧光液富集。图16给出上侧微管道荧光分布随时间的变化。中间峰值表示结合部下侧管道荧光富集，两旁低亮度区对应离子耗散。耗散区随时间逐渐拉长，两端的浓度跳跃区向外扩展。将N－S方程与Poisson方程及Nernst－Planck方程联立［32］，简化推导出耗散区浓度扰动传播方程为：

这是一维波动方程，Ci是第i种离子浓度，ux是流向速度，zi是离子化合物，F为法拉第常数，μi为离子迁移率，E为外加电场强度。公式（14）说明浓度扰动在初期以波动方式传播，正如图16中两实线表示的耗散区扩展的边界。而时间增加后，耗散区扩展减慢，此时L＊～更符合其传播规律（图16中虚线）。

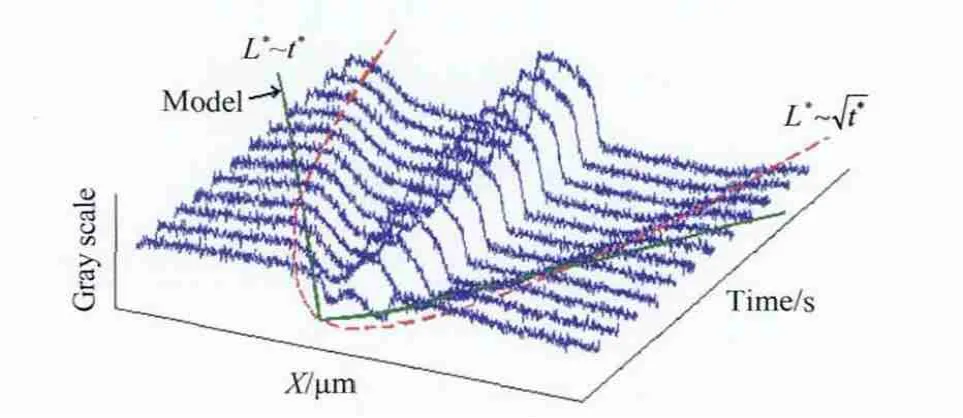
图16 离子耗散区荧光浓度分布随时间的变化［32］Fig.16 The temporal variation of the fluorescent concentration distribution in ion depletion zone

5.2 微纳组合管道中的旋涡运动

微纳复合管道中还观察到旋涡运动。使用200nm荧光粒子显示了三维微纳复合流道结合部的硼砂缓冲液（pH＝9.2）中的旋涡运动（见图17）［33］。图片拍摄曝光时间30ms，两帧时间间隔约100ms，由50帧连续拍摄的图片叠加而成。图24显示出在上下管道边各有一对旋涡，旋转轴垂直纸面；而管道中间有一对大旋涡，其旋转轴平行纸面。

图17 三维微纳复合流道结合部的旋涡运动［33］Fig.17 The vortex flow in the junction of a hybrid 3DMicro／Nano－channel

在电场驱动下的微纳复合管道中为什么会出现压力驱动下的旋涡运动？Chang等人观测了纳米缝隙两端生成的旋涡并系统介绍了浓差极化对旋涡生成的影响［34］。我们则根据涡量方程说明了涡量产生的根源：

其中ζi为第i分量的涡量，vi为速度，体积力gi＝curl（F）＝∇（c）×∇（ψ），浓度场梯度∇c与电场梯度∇ψ的叉乘导致了涡量的产生［35］。

6 有待研究的问题与展望

本研究围绕着连续性假设适用性、边界滑移、微纳粒子布朗运动和微旋涡运动等问题，介绍了Micro／NanoPIV、示踪粒子流场显示等技术应用于微纳流场观测的进展与难点。主要内容包括：连续性假设至少适用于10nm以上的流体流动；示踪粒子尺度及近壁粒子浓度的非线性分布对MicroPIV测量结果影响显著；尺度小于100nm的粒子表面特性对布朗扩散系数有重要影响；Janus粒子运动呈现明显的非高斯特性；近壁或狭窄管道中微纳粒子运动应考虑剪切流场、表面静电力、范德华力等对流体运动的影响；在微纳复合管道电驱动流会产生波传播、旋涡等多种动力学现象等。微纳米尺度下的流动测量扩展了经典实验流体力学研究内容，引入了新的测量手段，如MicroPIV、NanoPIV及AFM／SFA等，实验的空间精度可达到10nm量级，力的测量精度达到pN，时间分辨率达到ns，最小示踪粒子量子点直径可达几个nm。这些研究极大丰富了传统实验流体的测量技术。但目前仍有一些问题有待研究，如：

（1）微纳尺度气体流动测量

微纳尺度气体流动在能源与环境领域经常涉及，如页岩油气开采、大气雾霾PM2.5的检测等。微纳尺度气体运动速度测量与液体不同，气体分子自由程10～60nm，接近分子示踪物质的最小特征尺度。在选择示踪粒子及分析测量结果上应该有更特殊的考虑。

（2）多相流体界面测量

微纳尺度流动除单相连续流动外，大量应用问题涉及液滴、气泡、细胞等多相流动，如微流控芯片在器官组织培养上的应用等。在微纳尺度下，液滴／气泡的生存与传输条件与它们的界面（液／气／固）物性有关，而目前这类复杂流体界面区的测量还有待研究。

（3）带化学反应的流场测量

在微纳流动中化学能常被作为微推进器或换能器的动力，如API分子马达或Janus粒子等，化学能的定量分析对器件特性及设计非常重要。正如4.2节Janus粒子历经不同运动状态的根本原因是其表面化学反应的发生与衰减的影响，而我们对其定量分析知之甚少。

总之，随着微纳加工技术的发展，微纳器件应用将日益增加。微纳米流动测量将面临着许多新的挑战，也是一种机遇。目前微纳米流动测量仍然沿着经典流体力学测量的“小型化”的思路开展，而纳尺度的测量需要提出新的实验方法与技术。如在一些极复杂几何形状的介质中测量流动的速度和流量，仅测量终端的压力p和Q显然不够。深入介质内部显示流动应该寻找新的示踪物质，追踪分子量级示踪物质的技术需要将统计方法引入测量。当然流体力学基本的连续介质假设适用尺度下限（～1nm）和滑移边界条件的定量表达等也需要继续开展相应实验检验。我们相信微纳尺度实验流体力学在迎接上述挑战中将不断发展和成熟。

由于篇幅有限，微纳米气体测量及MEMS器件设计没有涉及，国内微流动方面的大量研究结果尚未引用，有兴趣的读者可参考相关论著［36－38］。

附录A

微纳米流动主要测量仪器的原理与性能介绍

（1）MicroPIV硬件系统可认为是宏观PIV与荧光显微镜的组合（见图A1）。其原理仍然是通过测量示踪粒子在给定时间内的位移获得速度，可采用自相关（auto－correlation）或互相关（cross－correlation）方法。测量时通过荧光显微镜观察（如100x／1.40物镜），因此必须采用荧光粒子，直径为100～500nm。测速范围1μm／s～10mm／s，Re＝0.01～10。我们用此方法测量液固界面附近区域的当地流体速度，再依据Navier提出来的线性滑移模型，获得滑移长度。

图A1 MicroPIV测量原理示意图［19］Fig.A1 The schematic of the principle of MicroPIV measurement

（2）NanoPIV测量系统可认为是MicroPIV与近场隐失波的组合，用于测量距离壁面500nm范围内的流场速度。隐失波的原理［39］是当光从光密介质射向光疏介质时（如穿过玻璃射向水），在玻璃与水界面处发生全反射，并产生沿水一侧传播的隐失波（图A2）。隐失波可以照亮界面附近，其穿透深度约200～500nm。界面附近隐失波光强I呈指数衰减，

其中穿透深度zp为：zp，这里n1和n2为介质折射率，λ为入射光波长，θ为入射角。实验中用吸附在壁面的静止荧光粒子作为亮度标准I0，测量流动的示踪粒子的亮度，依据光强指数衰减公式（A1）确定示踪粒子的z位置。沿用粒子追踪技术获得不同z位置的测量速度。目前我们测量速度剖面时使用示踪粒子直径20～200nm，测量距壁面约600nm以内。

图A2 隐失波原理示意图Fig.A2 The schematic of the principle of evanescent wave

（3）SFA／AFM（表面力测量仪／原子力显微镜）原本用于表面力测量，微纳流动实验中可用于测量滑移长度b，原理是基于探针小球接近平板时水动力学阻力Fh的滑移修正公式（见图A3（a））［40］：

其中，a为小球半径，μ为流体动力粘性，h为小球到平板距离，u为探针接近平板的速度。滑移修正因子为此方法测量时，h可达10nm量级，可实现纳米尺度界面力的测量。

另外，AFM原子力显微镜胶体探针还可以被用来测量液固界面附近的静电力及范德华力（图A3（b））。根据DLVO理论，胶体探针受到的合力可由下式表示［41］：

其中，A为Hamaker常数，a为胶体球半径，h为胶体球到基底的距离，ψ1和ψ2分别为胶体球和基底的表面电势，κ为德拜长度的倒数。

图A3 SFA／AFM测量装置示意图［19］［41］Fig.A3 The schematic of the SFA／AFM measurement principle and setup

图A4 pA电流计测量流向电流示意图［42］Fig.A4 The schematic of the streaming current measurement using pico－amperemeter

（4）pA电流计用于测量电解质溶液流动时电荷输运。由于液固界面双电层的存在，微纳尺度流动不可避免地伴随着电荷的输运并产生电流，例如流向电流和离子电流。流向电流［7］Ist是在压力驱动下流动携带双电层内净电荷运动而产生（见图A4），可由下式计算：

其中，ζ是管道壁面zeta电势，Δp为管道压力降，L为管道长，A为管道横截面积。离子电流Iion则是在电压V驱动下溶液中离子的定向输运形成的电流［7］：

其中σ为管道内溶液的表观电导率。

在使用（A4）式测量流向电流时需要满足一系列假设，比如薄双电层、弱电势等，否则会产生一定的误差。在纳米尺度流动中，如果发生双电层交叠，（A4）式将不适用。因此，较为准确的做法是联立Poisson－Boltzmann方程和流动N－S方程求解流动输运的电荷量来计算流向电流。实际测量中流向电流容易受负载等影响。考虑到压力输运电荷迁移后在管道两端会形成流向电势Ust，由压力驱动产生的流向电流和流向电势建立的离子电流平衡，即（A4）和（A5）式联立，求得（A5）式中的电压即为流向电势Ust：

流向电势和流向电流的测量方法类似，只需要将图A4中的pA电流计改成相应的电压测量装置即可，流向电势的测量和流向电流的测量可以互为补充。

借助MicroPIV、NanoPIV可直接测量微纳流动速度场，如果采用直径20nm的示踪粒子，测量位置可接近固壁至10nm左右。利用SFA／AFM可间接测量速度场，流动特征尺度小于10nm。利用pA流量计测量通道内流体或壁面的电荷输运，也可间接测量流动速度。

致谢：本文是根据2013年中国力学大会流体力学分会上的邀请报告及第八届全国实验流体力学会议上的大会报告整理而成，感谢《实验流体力学》杂志编辑部的约稿促使本文最终呈现给读者。文中所述本组工作受到973项目G1999033106（99／04），2007CB714701（07／11）、国家自然科学基金10272107（03／05），10672172（07／09），10872203（09／11），11272322（13／16），11202219（13／15）等项目经费支持，曾经有多位研究生参加了上述工作，在此一并致谢。

［1］ 李战华，吴健康，胡国庆，等.微流控芯片中的流体流动［M］.北京：科学出版社，2012.

［2］ Bocquet L，Charlaix E.Nanofluidics，from bulk to interfaceds［J］.Chem Soc Rev，2010，39：1073－1095.

［3］ Sparreboom W，Van den Berg A，Eijkel A.Transport in nanofluidic systems：a review of theorey and applications［J］.New J Phys，2010，12：015004.

［4］ Meinhart C，Wereley S，Santiago J.PIV measurements in a microchannel flow［J］.Exp Fluids，1999，27：414－419.

［5］ Huang P，Guasto J，Breuer K.Direct measurement of slip velocities usihng three dimensional total internal reflection velocimetry［J］.J Fluid Mech，2006，566：447.

［6］ Cottin－Bizonne C，Cross B，Steinberger A，et al.Bounmdary slip on smooth hydrophobic surfaces：intrinsic effects and possible artifacts［J］.Phys Rev Letters，2005，94：056102.

［7］ Kirby B，Hasselbrink Jr J.Zeta potential of microfluidic substrates［J］.Electrophoresis，2004，25：187－202.

［8］ Cui H H，Silber Li Z H，Zhu S N.Flow characteristics of liquids in microtubes driven by a high pressure［J］.Phys Fluids，2004，16：1803.

［9］ 李战华，崔海航.微尺度流动特性［J］.机械强度，2001，23（4）：476－480.Li Zhanhua，Cui Haihang.Characteristics of micro scale flow［J］.Journal of Mechanical Strength，2001，23（4）：476－480.

［10］Wereley S，Meinhart C.Recent advances in micro－particle image velocimetry［J］.Annu REv Fluid Mech，2010，42：557－576.

［11］Majumder M，Chopra N，Andrews R，et al.Nanoscale hydrodynamics：enhanced flow in carbon nanotubes［J］.Nature，2005，438：44.

［12］Holt J，Park H，Wang Y.Fast Mass transport through sub－2－ nanometer carbon nanotubes［J］.Science，2006，312：1034.

［13］Whitby M，Cagonon L，Tahanou M.Enhanced fluid flow through nanoscale carbon pipes［J］.Nano Letters，2008，8（9）：2632－2637.

［14］Qin X，Yuan Q，Zhao Y.Measurement of the rate of water translocation through carbon nanotubes［J］.Nano Letters，2011，11：2173－2177.

［15］Kannam S，Todd B，Hansen J.How fast does water flow in carbon nanotubes［J］.J Chem Phys，2013，138：094701.

［16］Vinogradova O.Drainage of a thin film confined between hydrophobic surfaces［J］.Langmuir，1995，11：2213－2220.

［17］Merabia S，sheogin S，Joly J，et al.Heat transfer from nanopaticles：a corresponding state analysis［J］.PNAS，2009，106（36）：15113－15118.

［18］Navier C.Memoire surles lois du movement des fluids［J］.Mem Acad Sci inst Fr，1823，6：389－416.

［19］Neto C，Evans D，Bonaccurso E，et al.Boundary slip in Newtonian liquids：a review of experimental studies［J］.Rep Prog Phys，2005，68（28）：59－97.

［20］Zheng X，Silber Li Z H，Kong G P.The influence of nano－particle tracers on the slip length measurements by micro PTV［J］.Acta Mechanica Sinica，2013，29：411－419.

［21］Zheng X，Silber Li Z H.Measurement of velocity profiles in a rectangular microchannel with aspect ratioα＝0.35［J］.Exp Fluids，2008，44（6）：951－959.

［22］Zheng X，Silber Li Z H.The influence of Saffman lift force on nanoparitcle concentration distribution near a wall［J］.Applied Phys Letters，2009，95（12）：124105.

［23］White F.Viscous fluid flow［M］.McGraw－Hill Book Company，1974.New York.

［24］郑旭，孔高攀，李战华.NanoPTV近壁分层速度测量［C］.第9届全国流动显示会议，云南，昆明，2012.

［25］Sendner C，Horinek D，Bocquet L.Interfacial water at hydrophobic and hydrophilic surfaces：slip，viscosity and diffusion［J］.Langmuir，2009，25（10）：768－781.

［26］Probstein R.Physicochemical hydrodynamics［M］.Butterworth Publishers，1989.

［27］王绪伟.纳米粒子受限布朗运动的实验研究［D］.北京：中国科学院力学研究所，2011.

［28］Zheng X，Wu M L，Gong C L.Measurement of diffusiophoretic motion of Janus micro－particles［C］.Proceeding of 12thAsian symposium on visualization.May 2013，Taiwan.

［29］Zheng X，Ten Hagen B，Kaiser A，et al.Non－Gaussian Statistics for the motion of self－propelled Janus particles：experiments versus theory［J］.Phys Rev E，2013，88：032304.

［30］Banerjee A，Kihm K.Experimental verification of near wall hidered diffusion for the Brownian motion of nanopairticles using evanescent wave microscopy［J］.Phys Rev E，2005，72（4）：042101.

［31］Lauga E.Apparent slip due to the motion of suspended particles in flow of electrolyte solutions［J］.Langmuir，2004，20（20）：8924－8930.

［32］Yu Q，Silber Li Z H.Measurements of the ion－depletion zone evolution in a micro／nano－channel［J］.Microfluid Nanofluid，2011，11：623－631.

［33］Silber Li Z H，Zheng X，Kong G P.Vorticies in micro／nanochannel flow［C］.9thconference on advances in fluid Mechanics.Split，Croatia，July 2012.

［34］Chang H C，Yossifon G，Demekhin E.Nanoscale electrokinedtics and microvortices：how microhydrodynamics affects nanofluidic ion flux［J］.Annu Rev Fluid Mech，2012，44：401－426.

［35］Silber LI Z H，Zheng X，Kong G P.vortices in micro／nano channel flows［J］.WIT transactions on engineering sciences，2012，74：533－545.

［36］林建忠，包福兵，张凯，等.微纳流动理论及应用［M］.北京：科学出版社，2010.

［37］赵亚溥.表面与界面物理力学［M］.北京：科学出版社，2012.

［38］林炳承.微纳流控芯片实验室［M］.北京：科学出版社，2013.

［39］Zettner C，Yoda M.Particle velocity field measuremtns in a near wall flow using evanescent wave illumination［J］.Exp Fluids，2003，34：115－121.

［40］Craig V，Neto C，Williams D.Shear－dependent boundary slip in an aqueous Newtonian liquid［J］.Phy Rev Letters，2001，87（5）：054504.

［41］Audry M C，Piednoir A，Joseph P，et al.Amplification of elctro－osmotic flows by wall slippage：direct measurements on OTS－surfaces［J］.Faraday Discussion，2010，146：116－124.

［42］Laffite G，Zheng X，Renaud L.Characterization of a surfacecharge modulation electrofluidic transistor by hydrodynamic measurements［J］.Int J Nanoscience，2012，11（4）：1240021.