基于代理模型的多体动力学模型修正技术

方剑光，高云凯，徐成民，张玉婷

(1．同济大学汽车学院，上海 201804;2．悉尼大学航空、机械和机电一体化工程学院，悉尼，NSW 2006)

前言

在汽车耐久性虚拟开发流程中，获得车身或其他部件正确的边界载荷，是准确预测其疲劳寿命的先决条件。通常，这些边界载荷从多体动力学仿真中提取［1－4］，因此建立高精度能反映实际动力学特性的模型对于后续的疲劳寿命预测尤为重要。

然而，建立多体模型过程中经常遇到的困难是模型中各个部件动力学特性表征参数的模拟，例如悬架系统阻尼参数等。为了获取这些参数，就要求进行室内台架或室外道路试验。而实际开发过程中很有可能会受到实验成本和开发周期等限制，这些参数无法获取，只能粗略估计，这就将造成模型的动力学性能较差。在这种情况下，对这些估计的参数进行简单的人工调整，往往很难达到理想的效果:首先，对每个参数进行调整无疑会降低效率;而且，由于非线性因素的存在，盲目地调整并不能得到正确的结果;此外，随着参数数量的增加，参数之间的交互作用也将增加人工调整的难度。

因此，本文中引入参数识别方法以实现多体模型的修正。文献［5］中将响应面模型用于5自由度动力学系统的参数识别，对于线性系统取得了成功，而对于非线性系统还有待深入。文献［6］中将参数识别定义为逆问题，在时域内通过全局和子结构法识别了弹簧和阻尼器的非线性参数。文献［7］中将正交分解与混合适应性群体智能算法相结合，根据测量的加速度信号在时域内识别结构的刚度和阻尼参数。

本文中将代理模型技术、优化技术与参数识别技术有机结合，以某试车场路面为例，高效地反算汽车多体动力学表征参数，实现多体模型的修正，旨在最大限度地降低汽车的开发成本和缩短开发周期。

1 模型修正方法

模型修正过程首先要求建立一个目标函数，即模型误差评价函数，它反映了一个物理系统的数值模型和试验模型之间在输出响应上的差异。一个最小二乘问题的目标函数可以定义为

式中:N代表实验曲线上取样点的个数，见图1;x为多体模型中待修正参数向量;Wi为第i个取样点的权系数;Ti为第i个取样点处的实验测量值;fi(x)为第i个取样点处近似模型的响应值;si为第i个取样点的残差比例系数;ei(x)为第i个取样点的残差值。本文中通过仿真和实验的时域曲线之间的差异来评价模型误差，N=512，Wi和si等于1。定义模型误差函数之后，模型修正问题就转化为通过调整模型参数使误差最小化的优化问题。

本文中将结合实验设计、代理模型技术和二次规划算法，实现用于耐久性分析的动力学模型的修正，流程如图2所示。

2 多体动力学建模及参数化

用MSC．ADAMS软件建立车辆的多体动力学模型，如图3所示。其中，前悬架为麦弗逊悬架，由减振器总成、摆臂、横向稳定杆和转向系统组成，后悬架为非独立悬架，由钢板弹簧、减振器、限位块和车桥组成。车身采用质量点建模，与悬架通过衬套连接。

在多体动力学模型中，非线性因素的存在无疑大大提高了模型的复杂程度，使模型修正更为棘手。考虑到减振器总成参数对整车动力学性能的重要性，本文中将悬架系统前减振器的阻尼特性和缓冲块刚度特性作为调整参数，考虑到左右对称性，以底盘左前悬架处与车身之间的相对位移信号来衡量多体模型的精确性，图4给出了已有同类车型减振器的相应特性。

由阻尼特性曲线可以看出，载荷与速度是多段线性关系:缓冲块刚度曲线可分为3段，当位移较小(即缓冲块起作用)时载荷为0，之后载荷线性增加，当缓冲块受挤压到一定程度时载荷成指数增加。因此，阻尼和刚度特性曲线可表述为

3 筛选参数

从众多影响模型精度的因素中筛选出最主要的几个因素，它们对参数识别的效率非常重要。在工业界，正交实验设计方法［8］已被广泛用作从众多影响因素中快速筛选出几个重要因素的一种快速有效的方法。采用三水平的L27正交表分析了表1中11个因素中对位移响应的影响。图5为各因素不同水平下误差评价函数的平均值。挑出影响最显著的5个变量 (v3、k1、k2、k3和 k5)作为模型修正参数，优化问题的变量为x=［v3k1k2k3k5］T。

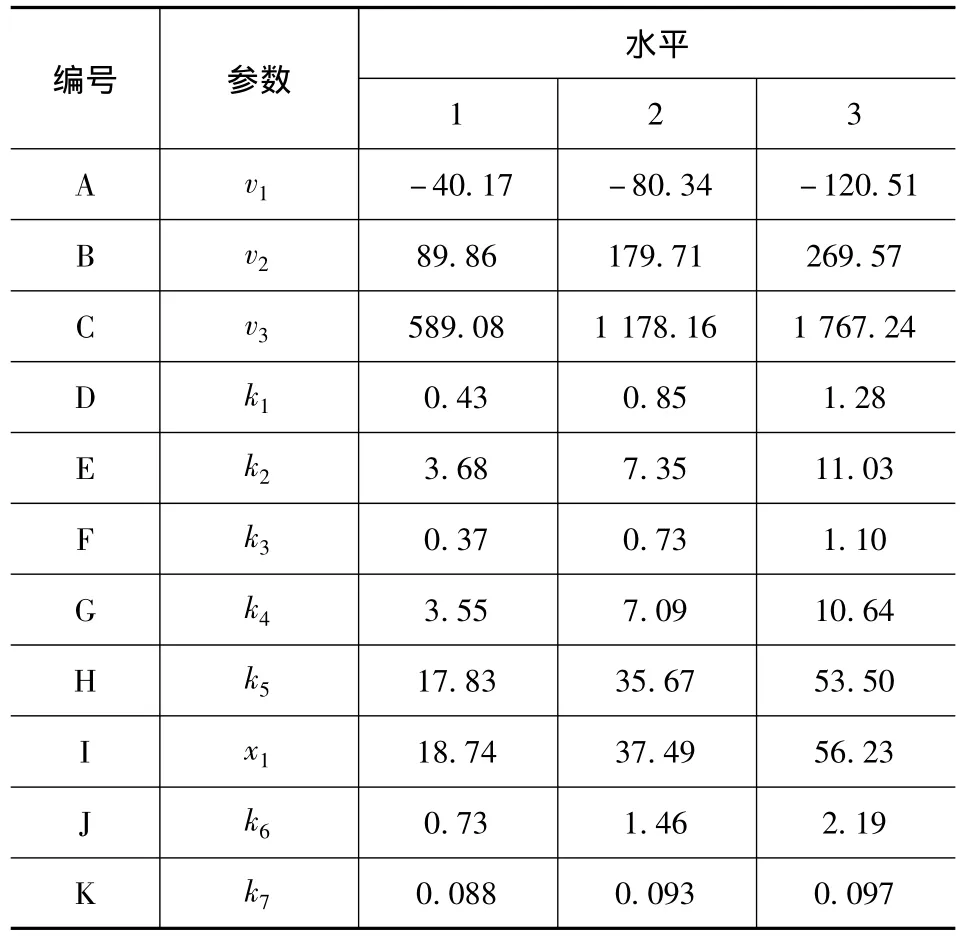
表1 正交试验设计参数信息

4 代理模型

在工程优化中，直接将仿真模型与优化算法耦合会导致优化过程的低效，因为优化迭代中仿真分析需要消耗大量的计算成本。此外，优化过程中多体动力学仿真中存在积分误差等带来的模型不稳定性，使得单次仿真失效而导致整个优化过程的终止。根据以上原因，采用基于代理模型的优化策略。代理模型可视为代替仿真模型，近似表达设计变量和响应关系的传递函数。将其代替仿真模型进行优化，可有效提高优化效率。

(1)响应面模型 响应面模型是最典型的代理模型，最早在1951年提出［9］。在工程上广泛应用的二阶响应面模型的数学表达式为

式中:y^为响应的估计值;xi为第i个输入变量;a0、ai、aii和aij为待定系数，由最小二乘法求得。

(2)径向基模型 径向基函数(radial basis function，RBF)是在1971年首次提出的一种用于离散多元数据的拟合方法［10］，其表达式为

式中:μ为多项式模型;‖x－xi‖是点x与xi的欧氏距离;φ是基函数;λi是基函数在取样点xi处的未知加权系数。因此，径向基函数模型实际上是由基于欧氏距离的径向对称基函数和多项式函数的线性组合。

关于基函数φ的形式，高斯函数和多重二次函数具有较好的整体特性［11］，其基函数形式如表2所示。c为自由形状参数。

表2 基函数

(3)Kriging模型 Kriging模型由全局近似模型与局部偏差结合而成［12］:式中:y(x)为待拟合的响应函数;f(x)通常是多项式响应面近似模型，一般被看作常数，提供设计空间的全局近似模型;Z(x)是期望为零，方差为σ2和协方差为非零的随机偏差，提供局部偏差，使得Kriging模型可在ns个样本点做插值。Z(x)的协方差矩阵为

Cov［Z(xi)，Z(xj)］ = σ2R［R(xi，xj)］ (5)式中:R为相关矩阵，是对角线上全为1的(ns×ns)对称矩阵;R(xi，xj)为ns中任意两个样本点xi和xj的相关函数，一般采用高斯相关函数:

式中:θk为用于拟合近似模型的未知相关系数;xi

k和xj

k分别为样本点xi，xj第k个元素。

响应y在未知位置x点的估计值y^为

其中:

式中:y为ns个样本点的响应列向量;f为长度为ns的单位列向量;rT(x)为ns个样本点 x1，…，xn{

}

s与未知位置x所组成的相关向量:

其中:

详细过程参考文献［13］。

代理模型仅仅是对复杂仿真分析模型的简化和近似，因此，在求出代理模型的待估参数后，须对代理模型进行统计检验，评估代理模型对真实响应的逼近程度。在精度不高的代理模型基础上获得的最优结果不但不能指导设计，反而会误导设计，因此，对代理模型的误差进行评估至关重要。常用的误差估计准则有:决定系数 R2、相对平均绝对误差(RAAE)和相对最大绝对误差(RMAE)。

式中:yi、y^和y－分别为第i个检验点响应量的实测值、响应量的预测值和响应量实测值的平均值;q为检验点的个数。

从上述的定义式可以看出，R2的取值在［0，1］区间内，R2越接近于1，表明回归拟合的效果越好。此外，R2和RAAE为全局指标，而RMAE是一个局部指标，其重要性不如R2和RAAE。但是，即使R2较大，RAAE较小，大的RMAE也能表明在设计空间的某个区域的精度较差。在实际应用中，经常根据R2的值来判断代理模型的拟合精度。

建立高精度的近似模型，很大程度上取决于对设计空间的采样技术。用合理的实验设计方法均匀分布样本点，可以有效地体现设计空间的特征，保证近似模型的精度。文中采用文献［14］中提出的优化拉丁方(optimal latin hypercube，OLH)对空间采样，生成随机均匀分布的50个样本点。

采用上述的3种代理模型，对样本点进行拟合，评价各种模型的精度，如表3所示。由表可见，径向基模型在整体和局部的精度都很差;而响应面和Kriging模型表现出更好的性能，最终选取Kriging模型用于后期的参数修正。

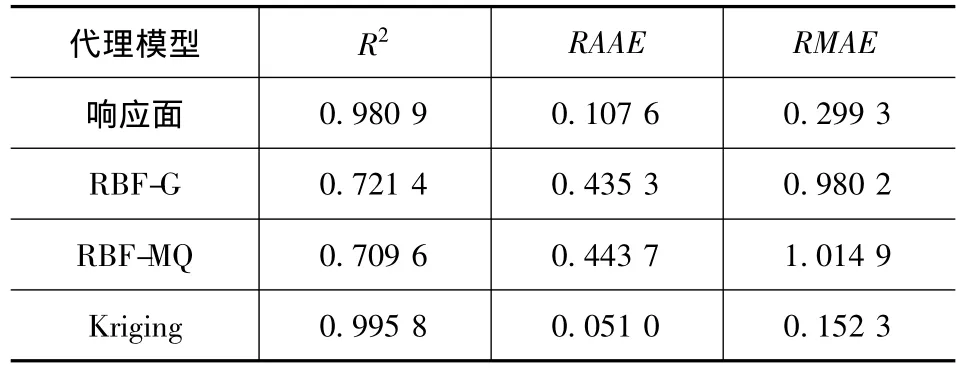
表3 代理模型的精度评价

5 模型修正结果

基于建立的车身与底盘间相对位移的Kriging模型，本文中采用序列二次规划优化算法使模型误差E(x)最小化。E(x)的优化历程如图6所示，可见经过103步迭代，E(x)由122收敛于25.67。将优化得到的参数代入式(2)和式(3)，得到减振器阻尼和缓冲块刚度特性。图7给出了修正前后阻尼和刚度特性。根据修正结果，更新多体动力学模型。图8为车身与底盘左前悬架处相对位移修正仿真值和实验值的对比。可以看出，经参数识别后的修正模型仿真结果与试验非常接近。

6 结论

(1)使用正交试验设计，从众多参数中筛选出对模型准确性影响显著的参数，可以提高模型修正的效率。

(2)采用优化拉丁方实验设计对设计空间均匀采样，并通过3种类型代理模型的对比研究发现，Kriging模型具有较高的精度。

(3)模型修正后的仿真结果逼近实验值，可为后期耐久性的准确预测奠定基础。

(4)利用模型修正技术获得汽车悬架非线性动力学特性，可大大降低开发成本，缩短开发周期。该技术可以推广至其他相关领域。

［1］ 高云凯，李翠，崔玲，等．燃料电池大客车车身疲劳寿命仿真分析［J］．汽车工程，2010，32(1):7－12．

［2］ 孟瑾，朱平，胡志刚．基于多体动力学和有限元法的车身结构疲劳寿命预测［J］．中国公路学报，2010，23(4):113－120．

［3］ 赵婷婷，李长波，王军杰，等．基于有限元法的某微型货车车身疲劳寿命分析［J］．汽车工程，2011，33(5):428－432．

［4］ Kim H S，Yim H J，Kim CB．Computational Durability Prediction of Body Structure in Propotype Vehicles［J］．International Journal of Automotive Technology，2000，23(1)．

［5］ Rutherford A C，Inman D J，Park G，et al．Use of Response Surface Metamodels for Identification of Stiffness and Damping Coefficients in a Simple Dynamic System［J］．Shock and Vibration，2005(12):317－331．

［6］ Kumar R K，Shankar K．Parametric Identification of Structures with Nonlinearities Using Global and Substructure Approaches in the Time Domain［J］．Advances in Structural Engineering，2009，12(2):195－210．

［7］ Rama Mohan Rao A，Lakshmi K．Parameter Estimation Technique Combining Pod with Hybrid Adaptive Swarm Intelligence Algorithm［C］．Proceedings of International Conference on Advances in Civil Engineering ACE-2011，21－23 October 2011:57－63．

［8］ Mohan L V，Shunmugam M S．An Orthogonal Array Based Optimization Algorithm for Computer-aided Measurement of Worm Surface［J］．International Journal Advanced Manufacture Technology，2006，30(5 －6):434 －443．

［9］ Box G E P，Wilson K B．On the Experimental Attainment of Optimum Conditions［J］．Journal of the Royal Statistical Society B，1951，13(1):1 －45．

［10］ Hardy R L．Multiquadric Equations of Topography and Other Irregular Surfaces［J］．Journal of Geophysical Research，1971，76(8):1905－1915．

［11］ Mcdonald DB，Grantham W J，Tabor W L，et al．Response Surface Model Development for Global/local Optimization Using Radial Basis Functions［C］．Presented at the 8th AIAA Symposium on Multidisciplinary Analysis and Optimization，Long Beach，CA，2000．

［12］ Simpson T W，Mistree F．Kriging Models for Global Approximation in Simulation-based Multidisciplinary Design Optimization［J］．Aiaa Journal，2001，39(12):2233 －2241．

［13］ Cressie N．Geostatistics［J］．The American Statistician，1989，43(4):197－202．

［14］ Jin R，Chen W，Sudjianto A．An Efficient Algorithm for Constructing Optimal Design of Computer Experiments［J］．Journal of Statistical Planning and Inference，2005，134(1):268－287．