不同基准下坐标转换的方法及注意事项

孙艳崇 SUN Yan-chong

（辽宁省交通高等专科学校，沈阳 110122）

（Liaoning Provincial College of Communications，Shenyang 110122，China）

不同基准下坐标转换的方法及注意事项

孙艳崇 SUN Yan-chong

（辽宁省交通高等专科学校，沈阳 110122）

（Liaoning Provincial College of Communications，Shenyang 110122，China）

不同基准的坐标转换，如果其转换范围较大，都是在空间直角坐标系下进行的；如果其坐标的表示形式是大地坐标或高斯平面坐标，则需要首先将其转换成空间直角坐标，然后才能依据转换参数及模型进行转换。本文以一个实例，叙述了不同基准坐标转换的具体过程。

基准；坐标转换；模型

1 不同基准坐标的转换概述

测量常用坐标系有三种不同的表示方法：大地坐标系（经纬度和高程），空间直角坐标系（X横坐标、Y纵坐标、Z竖坐标），高斯平面直角坐标系（平面坐标和高程），这三种坐标系都是同椭球的几何参数相关的，其坐标的表达都是等价的，可以相互进行转换的。

两个不同基准的坐标转换一般而言，比较严密的是七参数法：即X平移，Y平移，Z平移，X旋转，Y旋转，Z旋转，尺度变化K，要计算出七参数就需要在一个地区需要3个以上的已知点（每个点都有源坐标系下的坐标和目标坐标系下的坐标）；如果转换范围不大，最远点间的距离不大于30Km（经验值），可以用三参数：即X平移，Y平移，Z平移，而将X旋转，Y旋转，Z旋转，尺度变化K视为0，所以三参数只是七参数的一种特例。

2 不同基准坐标的转换方法

基于不同基准（椭球）之间坐标系的转换，是在空间直角坐标系框架内实现的，例如WGS84大地坐标转换成1980年大地坐标，其转换过程如下：

①WGS84大地坐标依据WGS84椭球的几何参数，转换成WGS84空间直角坐标；

②依据转换参数及转换模型，WGS84空间直角坐标转换成1980空间直角坐标；

③1980空间直角坐标依据1980椭球的几何参数，转换成1980大地坐标。

基于两个空间直角坐标的转换模型，可以实现卫星网与地面网间的转换，这种转换在GPS测量中有着很重要的作用。自20世纪60年代以来，各国大地测量学者对此作了大量的研究，获得了多种转换方法及模型，这里只介绍3参数法和7参数法的转换模型。

2.1 三参数法 设两个空间直角坐标系分别为新坐标系OT-XTYTZT和旧坐标系O-XYZ，这两个坐标系各对应坐标轴相互平行，坐标系原点不相一致，如图1所示。不难看出，这两个坐标系中的同一点的坐标具有如下关系：

式中，ΔX0、ΔY0、ΔZ0是旧坐标系原点 O 在新坐标系OT-XTYTZT中的三个坐标分量，也称为三个平移参数。

三参数空间直角坐标间的转换公式，是在假设两坐标系之间各坐标轴相互平行的条件下导出的，这在实际上往往是不可能的，但由于各种基于椭球的坐标，其椭球都是经过定位的，所以实际上，两个空间直角坐标系下的X,Y,Z三个轴都是基本平行的（即旋转角度接近于0），所以在实际工作中，如果测区范围不大，经常采用三参数法进行坐标转换。

2.2 七参数法 两个空间直角坐标系除了三个平移参数外，当各坐标轴间相互不平行时，还存在有三个欧勒角，称之为三个旋转参数和一个尺度变化参数，所以共计有七个参数。七参数坐标转换有多种计算公式，这里只介绍布尔沙转换公式。

若以(Xi,Yi,Zi)TT和(Xi,Yi,Zi)分别表示Pi点在空间直角坐标系 OT-XTYTZT和 O-XYZ 中的坐标；(ΔX0，ΔY0，ΔZ0)表示原点坐标平移量。布尔沙7参数换算公式为

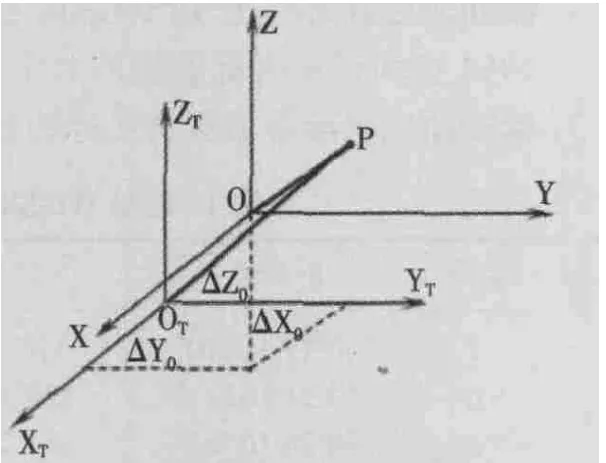
图1 三参数坐标转换

式中，（εx，εy，εz）三个坐标轴的旋转角度参数，dK为尺度比变化参数。

2.3 坐标转换实例 如表1所示：已知WGS84大地坐标，需要将其转换成北京1954高斯平面直角坐标，转换参数如表2所示（已知WGS84空间直角坐标转换成北京1954空间直角坐标转换的七个参数，和北京1954大地坐标转换成高斯平面直角坐标的投影参数）。

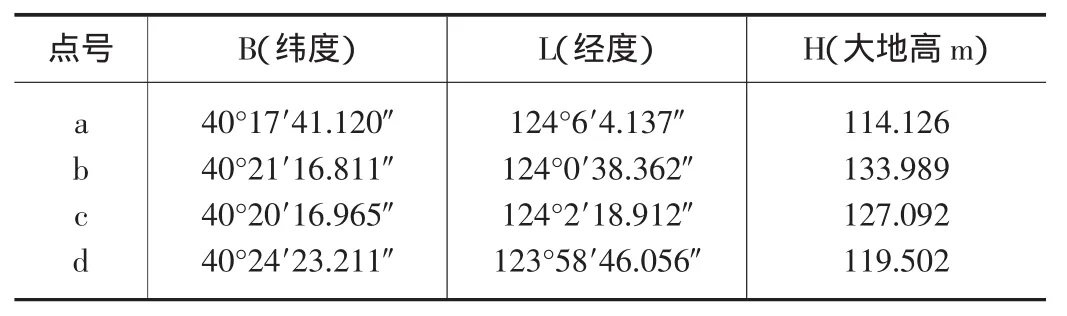
表1 已知WGS84大地坐标

表2 七参转换参数和高斯投影参数

其转换过程如下：

WGS84大地坐标（如表1所示）依据同一椭球基准的坐标转换方法，转换成WGS84空间直角坐标；然后依据转换七参数，转换成如表3所示的北京1954空间直角坐标；最后1954空间直角坐标转依据表2中的投影参数，转换成如表4所示的1954高斯平面直角坐标。

3 结束语

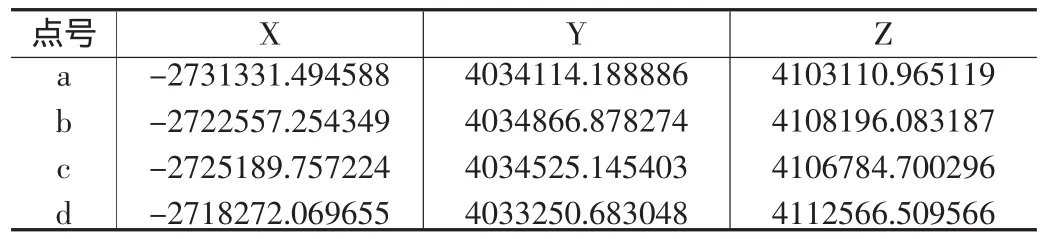
表3 北京1954空间直角坐标

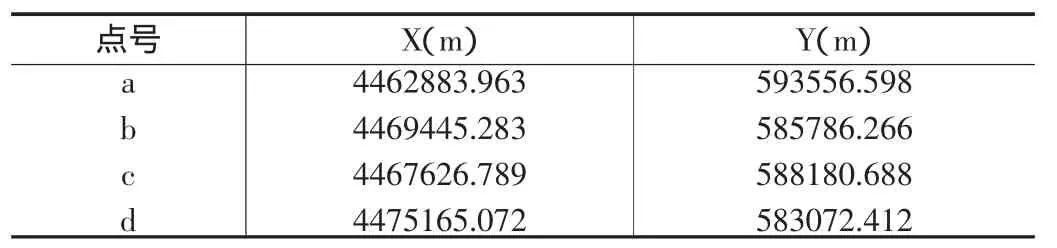
表4 北京1954高斯平面直角坐标

七参数法用于不同基准下坐标的转换从数学角度上讲是严密的，但实际上由于大地高不能精确的获得，从而导致此种坐标转换范围是有一定限制的，具体的转换范围通常通过转换后的残差确定，根据经验，一般100Km范围内是可以的，所以在WGS-84坐标和北京1954坐标之间是不存在一套转换参数可以全国通用的，是根据测区的实际情况分区域进行转换的。

[1]李征航，黄劲松.GPS测量与数据处理[M].武汉大学出版社，2005.

[2]孙艳崇.RTK两种坐标转换的数学模型及适用条件[J].沈阳：北方交通，2009.

[3]林玉祥.控制测量技术[M].北京：测绘出版社，2013.

Coordinates Transformation Method and Matters Needing Attention under the Different Datum Ellipsoid

Coordinate transformations under different datum ellipsoid,if the conversion range widely,are based on the space rectangular coordinates;if surveying coordinates are in the form of geodetic coordinate or Gauss plane coordinates,it need to be firstly converted into a rectangular space coordinates,and then to be converted on the basis of transformation parameters and model.Through an example,the paper describes the specific process of different reference coordinate.

datum ellipsoid；coordinate transformations；model

孙艳崇（1978-），男，辽宁绥中人，硕士研究生，讲师，教师，研究方向为数字化测图技术。

P208

A

1006-4311（2014）11-0241-02